Long-term exchange rates: the monetary approach
| Professeur(s) | |
|---|---|
| Cours | International Economy |
Lectures
- Ricardo's model: productivity differences as a determinant of trade
- The Heckscher-Ohlin model: differences in factor endowments as a determinant of trade
- Economies of scale as a determinant of trade: beyond comparative advantage
- Trade policy instruments
- Multilateral trade agreements
- Preferential Trade Agreements
- The Free Trade Challenge
- International Macroeconomics: Issues and Overview
- National Accounts and Balance of Payments
- Exchange rates and the foreign exchange market
- Short-term exchange rates: the asset-based approach
- Long-term exchange rates: the monetary approach
- Domestic product and short-term exchange rates
- Floating exchange rates
- Fixed exchange rates and intervention on the foreign exchange market
What are the determinants of the expected exchange rate?
What is absolute and relative purchasing power parity (PPP)?
What are the predictions of the monetary approach on the long-term evolution of the exchange rate?
What is the real exchange rate?
How can the monetary approach be generalized to take account of both real and monetary shocks in determining the long-term exchange rate?
As we have seen, the LT exchange rate is influenced by changes in the money supply.
The task now is to develop a model of exchange rate behaviour over the long run that links monetary policy and inflation to the interest rate and the exchange rate to explain how expectations about exchange rate movements are formed. Since short-term movements depend on long-run expectations, this model will also be important to explain the behaviour of in the short run.
In the long run:
- the general price level is variable (as are relative prices)
- Capital stock accumulation = we can now speak of GDP growth ( is no longer given), disregarding the cyclical fluctuations around this long-term trend. The GDP growth rate remains exogenous to the model. For a completely endogenous GDP we will have to wait for the next chapter.
Before developing a model of exchange rate determination in the long term, we will first define the absolute purchasing power parity (PPP) relationship that links exchange rate movements to movements in price levels. Then we will define the relative PPP that links exchange rate movements to inflation differentials.
The monetary model from the previous chapter is then grafted onto PPP. We will then have a theory (known as the long-run monetary approach) to explain long-term nominal exchange rate variations caused by monetary phenomena or by GDP growth. NB: this model describes the behaviour of the exchange rate in the long term and cannot be used to explain day-to-day exchange rate fluctuations (even if they are influenced by agents' expectations).
Finally, PPP is criticised by analysing the sources of its non-verification, which are just as many factors explaining fluctuations in the real exchange rate. A general model of the long-run equilibrium is derived.
Purchasing Power Parity (PPP)[modifier | modifier le wikicode]
The Law of One Price and Absolute PPP[modifier | modifier le wikicode]
PPP is based on the "law" of one price.
A) Law of One Price (UPA)
- [1]
where , are the prices of the good .
The good is tradable => subject to arbitrage between the two markets. Hp: no barriers to trade or transport costs.
B) Purchasing power parity (absolute)
- [2a]
where , are price indices (e.g. CPI). Same concept of the LPU, but on a basket of goods.
Verification requirements of [2a]:
- (i) All goods are tradable.
- (ii) LPU satisfied for each good.
- (iii) Identical consumer baskets (same goods and same weight).
Absolute PPP[modifier | modifier le wikicode]
Historically: PPP = decision guide for fixing the exchange rate (e.g. post WWI):
- [2b]
If, for example, , foreign goods are relatively more expensive than domestic goods (say x%) and foreign currency is relatively expensive (overvalued by x% relative to the PPP value).
If, for example, , foreign goods are relatively cheaper than domestic goods (say x%) and the foreign currency is relatively cheap (undervalued by x% relative to the PPP value).
The exchange rate defined by PPP is a kind of theoretical, long-term exchange rate. If the exchange rate observed in reality is higher than the rate indicated by the ratio of price indices, it is deduced that the national currency is undervalued.
Big Mac Index[modifier | modifier le wikicode]
The Big Mac Index is published by The Economist as an informal way of measuring the purchasing power parity (PPP) between two currencies and provides a test of the extent to which market exchange rates result in goods costing the same in different countries. The index, created in 1986, takes its name from the Big Mac, a hamburger sold at McDonald's restaurants.[10]
Application : Big Mac Index[11]
Idea: consider the big mac as a basket of goods (same ingredients everywhere, traded on the world market => the LPU should be checked), with prices and . The ratio between the two prices gives the theoretical exchange rate :
where reflects the long-term equilibrium exchange rate.
The relative deviation from the current exchange rate, , establishes the margin of overvaluation against the dollar (* = US) :
- if : we can expect a depreciation of the currency.
- if Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle m_{sur} < 0} : currency appreciation can be expected.
According to this criterion, at that time the CHF was overvalued -> expected depreciation.
Is the absolute PPP verified?[modifier | modifier le wikicode]
No sign of convergence in Hong Kong... maybe in Ireland... or England in the late '80s.
In general, lasting deviations from the theoretical relationship.
Relative purchasing power parity[modifier | modifier le wikicode]
As lasting deviations from the absolute PPP relationship are observed, there is a softer version of PPP, called relative PPP, in which the exchange rate Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle E} is equal to the ratio of price to a constant deviation factor ready i.e. with , constant. This implies that varies in direct proportion of and in inverse proportion of . In other words, this implies that :
where is the growth rate of , the rate of depreciation of the national currency and and inflation rates in and .
Relative PPP therefore equates the rate of depreciation of the national currency with the inflation rate differential between and . It is less restrictive (more general) than absolute PPP (i.e. if absolute PPP is verified, so is PPP, but the reverse is not true).It is less restrictive (more general) than absolute PPP (i.e. if absolute PPP is verified, so is PPP, but the reverse is not true).
The monetary approach[modifier | modifier le wikicode]
« Building blocs »[modifier | modifier le wikicode]
The monetary theory developed in chapter 12 shows us that in the long run the general price level is determined by the supply and demand for money :
The purchasing power parity theory developed at the beginning of this chapter shows us that the general price level influences the exchange rate :
The monetary approach[modifier | modifier le wikicode]
Assumptions:
- Long term: prices and wages "adjust instantaneously" to maintain full employment conditions in all markets.
- is fixed at its "full employment" level, , reflecting production conditions, and is insensitive to cyclical fluctuations.
- Only monetary factors (money supply and demand for money) are involved in the determination of the exchange rate: the exchange rate is explained by the ratio of prices in the two countries, and prices adjust so that the real money supply equals the real money demand.
Joint determination of , and by :
- [2b]
- [3]
The relative supply and demand for money determine price levels, which in turn determine the long-term exchange rate.
Chocs[modifier | modifier le wikicode]
Comparative static (equilibrium shocks)
1) Expansionary monetary policy in :
- ↗ => [3] : ↗ => [2b] : ↗ (= depreciation)
2) Growth in :
- ↗ => [3] : ↗ => ↘ => [2b] : ↘ (= appreciation)
3) Increase of :
- ↗ => [3] : ↘ => ↗ => [2b] : ↗ (= depreciation!)
The 3 changes affect the supply or demand for money, which leads to changes in prices to maintain equilibrium, which causes an adjustment of the exchange rate to maintain PPP (immediate jump in all variables).
Predictions 1) and 2) are in line with the monetary model without PPP (long-run effects). Apparently 3) is problematic, as this result contradicts ch. 11 and 12 (where if ↗ => more attractive CHF investments => ↘).
Short- and long-term interest rate[modifier | modifier le wikicode]
This apparent contradiction derives from the fact that the sources of interest rate fluctuation () are not the same in the short and long term, due to the different behaviour of the general price level, .
- in the short term (chp. 11 and 12) is fixed => it is that has to adjust to rebalance the money market when or changes level.
- In the long run (chp. 13) is flexible => it is that adjusts to rebalance the money market when or changes level, without affecting the value of .
But then: what does it depend on in the long run? Answer: on the equalisation of expected real interest rates (Fisher relation) :
Problem: Requires work on the dynamic version of the monetary model.
Summary: monetary model[modifier | modifier le wikicode]
Could be used as a basis for the formation of exchange rate expectations () that intervene in the interest rate parity.
Problem: based on PPP which is poorly verified
A general long-run model: the real exchange rate approach[modifier | modifier le wikicode]
Exchange rates and general price level[modifier | modifier le wikicode]
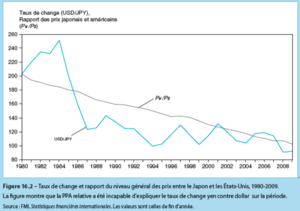
The PPP is not verified either in its absolute or relative version.
Main sources of non-verification of PPP[modifier | modifier le wikicode]
There are three main sources of non-verification of PPP :
- Contrasting what the SPA says, the existence of transportation costs and trade restrictions restricts trade in certain goods and services.
- Situations of monopoly and market power in certain sectors further weaken the link between the prices of identical goods sold in different countries.
- The structure of consumption is not the same in all countries => inflation statistics are based on different baskets of goods => there is no reason to check PPP even in the absence of trade barriers.
Nevertheless, the theory that the exchange rate and the general price level are linked in the long run is a simple and useful starting point → generalization of the PPP principle by introducing the concept of the real exchange rate.
The real exchange rate[modifier | modifier le wikicode]
The real exchange rate (RER), denoted , is defined as :
- [6]
Two interpretations:
1) Deviations from PPP:
- If absolute PPP is verified, ⟺ any value of reflects a deviation from absolute PPP.
- If relative PPP is true, is constant ⟺ any fluctuation of reflects a deviation from relative PPP.
2) Relative price of foreign products (relative to domestic products) = Indicator of the international competitiveness of domestic products: the higher the general level of foreign prices relative to the domestic economy, the more attractive domestic products are.
In reality, is different from and fluctuates = lasting and variable deviations from the theoretical relationship are observed.
General long-term model: the role of the RER[modifier | modifier le wikicode]
Idea: Complete the monetary model by accounting for real exchange rate changes = PPP dissatisfaction.
Problem: What are the determinants of ?
Solution adopted here : approximately reflects the relative price of foreign products compared to domestic products. Real depreciation (↗) -> the basket of goods produced abroad is + expensive (you need more domestic goods for the same quantity of foreign goods). Real appreciation (↘) -> the basket of goods produced abroad is - expensive (vice versa).
The equilibrium level of '' will be that which equals the relative demand for domestic products. () the relative supply of domestic products ().
The equilibrium RER[modifier | modifier le wikicode]
Since we are at long-run equilibrium, we will assume that the relative supply, RS, is equal to the ratio of full employment production levels : .
Relative demand, RD, is a positive function of the relative price of foreign products : , with .
The equilibrium RER is obtained when :
- [7]
Comparative Static :
- if requested for ↗ => (excess demand) ↘
- if offer of ↗ (growth) => (oversupply) ↗
General long-term model[modifier | modifier le wikicode]
The long period model (where is determined in [7]) becomes :
- [6]
- [7]
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {M}{P} = L(Y_{PE}, R)} [3]
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle frac {M^*}{P^*}= L(Y_{PE}^*, R^*)} [4]
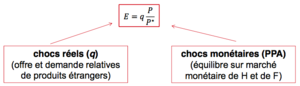
Compared to the monetary approach (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q = 1} ), only the first equation changes. It decomposes the sources of exchange rate fluctuations into monetary shocks (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \Delta P} , Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \Delta P^*} ) and real shocks (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \Delta q} ) and takes account of non-monetary factors implying lasting deviations in PPP.
Shocks[modifier | modifier le wikicode]
1. Expansionary monetary policy in Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H} :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle M} ↗ => [3]: Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle P} ↗ => [6] : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle E} (idem to the monetary model)
2. Increase in relative demand for Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H} :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q} ↘ (appréciation réelle) => [6] : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle E} ↘ (nominal appreciation)
3. Growth in Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H} (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Y_{PE}} ) 2 effects:
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q} ↗ (dépréciation réelle) => [6]: Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle E} ↗
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle :L} ↗ => [4] : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle P} ↘ => [6]: Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle E} ↘
Any monetary disturbance influences Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle E} according to PPP and any real disturbance influences Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle E} through Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q} . When the disturbances concern the goods market, exchange rate movements do not check PPP, even in the long term.
Summary: Long-term equilibrium[modifier | modifier le wikicode]
6] is used as a basis for the formation of exchange rate expectations (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle E^e} ) that intervene in the interest rate parity. The long-term exchange rate model developed in this chapter sheds light on how expectations (which influence the short-term exchange rate) are formed.
Last problem: variations of Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Y} in the short term: chapter 14.
Annexes[modifier | modifier le wikicode]
References[modifier | modifier le wikicode]
- ↑ Page personnelle de Federica Sbergami sur le site de l'Université de Genève
- ↑ Page personnelle de Federica Sbergami sur le site de l'Université de Neuchâtel
- ↑ Page personnelle de Federica Sbergami sur Research Gate
- ↑ Céline Carrère - Faculté d'économie et de management - UNIGE
- ↑ Céline Carrère - Google Scholar Citations
- ↑ Director Céline Carrère - Rectorat - UNIGE
- ↑ Céline Carrère | Sciences Po - Le Laboratoire Interdisciplinaire d'Evaluation des Politiques Publiques (LIEPP)
- ↑ Céline Carrere - EconPapers
- ↑ Céline Carrère's research works - ResearchGate
- ↑ Wikipedia contributors. (2020, March 18). Big Mac Index. In Wikipedia, The Free Encyclopedia. Retrieved 20:09, March 25, 2020, from https://en.wikipedia.org/w/index.php?title=Big_Mac_Index
- ↑ The Economist: http://www.economist.com/markets/Bigmac/
























































![{\displaystyle E=[q][{\frac {P}{P^{*}}}]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/1b2b3cef4cb070ae1a1362f0faf77b536eae187f)