Exchange rates and the foreign exchange market
| Professeur(s) | |
|---|---|
| Cours | International Economy |
Lectures
- Ricardo's model: productivity differences as a determinant of trade
- The Heckscher-Ohlin model: differences in factor endowments as a determinant of trade
- Economies of scale as a determinant of trade: beyond comparative advantage
- Trade policy instruments
- Multilateral trade agreements
- Preferential Trade Agreements
- The Free Trade Challenge
- International Macroeconomics: Issues and Overview
- National Accounts and Balance of Payments
- Exchange rates and the foreign exchange market
- Short-term exchange rates: the asset-based approach
- Long-term exchange rates: the monetary approach
- Domestic product and short-term exchange rates
- Floating exchange rates
- Fixed exchange rates and intervention on the foreign exchange market
What is the link between the balance of payments and the foreign exchange market?
What is the exchange rate of a currency and what are its main sources of fluctuation?
Who are the main players in the foreign exchange market?
What is the forward exchange rate?
What is the role of expectations in the foreign exchange market?
What is the relationship between the interest rate and the exchange rate?
Is the foreign exchange market efficient?
Reminder: neglecting the capital account () to simplify the analysis, the balance of payments equilibrium is written as follows: .
Both CC and CF depend on the exchange rate, = price of one currency in terms of another currency.
Within CF, it is useful to distinguish between private transactions, , and the reserve assets, RES, the latter being assumed to be independent of . Then we get:
Two approaches to the determination of the equilibrium exchange rate related to two different historical situations :
- Current account approach (1950-70)
- Approach by financial account (>1970)
- 1) Current account approach (1950-70):
is exogenous = control of international capital flows. is determined by the current transactions -> flow balance. Historically, controls on capital movements (poorly integrated financial markets) until the early 1970s => fixed, but adjustable (Bretton Woods regime).
- 2) Financial Account Approach (1970+)
is exogenous = capital flows are free, and react much faster than real (fixed short-term) transactions. is determined by the capital transactions balance of stocks. Historically, integrated financial markets since the 1970s => flexible.
The foreign exchange market[modifier | modifier le wikicode]
Foreign exchange quotation conventions[modifier | modifier le wikicode]
Rating conventions[modifier | modifier le wikicode]
In this lecture, writing XXX/YYYY indicates the number of units of currency XXX that is needed for one unit of currency YYY, regardless of whether XXX is the domestic or foreign currency.
Therefore, regardless of the quotation conventions, if we find 1.10 XXX/YYYY, it means that we exchange 1.10 units of XXX for 1 unit of YYYY. This is just a simple rating convention and as such is obviously not universal. The FT, for example, and many newspapers adopt the same notation, but the KO (as well as the quotation agency Reuters) adopts the reverse presentation convention (in the KO 1.10 XXX/YYYY indicates that 1.10 units of YYY are needed for 1 XXX).
Concretely, in the following, given the rating and quotation conventions adopted, 1.26 CHF/USD means that 1.26 Swiss francs are needed for 1 US dollar and that the Swiss franc is the national currency (=> if the rate were to rise to 1.33 this would indicate a depreciation of the CHF).
Exchange rates and prices of goods[modifier | modifier le wikicode]
As discussed in the lecture on national accounts and balance of payments, the exchange rate is used to compare the prices of goods sold in different locations. Effects of a change in the exchange rate on the prices of goods :
A depreciation of the national currency (CHF) reduces the relative price of the exported goods (watches in the example opposite). See also Box 13.1 of the KO on overnight stays of US tourists in Paris and the EUR/USD rate.
The foreign exchange market[modifier | modifier le wikicode]
Main players in the asset market: Commercial banks (main player: the 10 largest banks account for 75% of the market) and the interbank market ('wholesale' market); commercial companies (operating in several countries); non-bank financial institutions, e.g. pension funds (since the deregulation of financial markets); central banks (small volume of transactions when they are involved but high impact because of the signal effect).
Amounts: Trading volume around $1500 billion per day. In 6 days one exceeds world trade by one year!
Characteristics: Exchange of currencies on many financial markets, with few opportunities for effective arbitrage because information circulates very quickly. The USD is still the dominant vehicle currency as most transactions are still between one currency and the USD.
Spot exchange rate[modifier | modifier le wikicode]
Spot foreign currency transactions use spot exchange rates ( or sometimes for spot exchange rate). The validation day of a cash transaction = (2 days after the conclusion of the transaction).
When transactions specify a release date with (for example d = 30, d = 60, d = 90), the rates used are forward exchange rates. ( = forward exchange rate). Cf. later.
A foreign exchange swap or currency swap is a spot sale of a currency combined with a forward purchase of the same currency.
Arbitrage ensures that there are no major differences between, for example, and
Example of quotations[modifier | modifier le wikicode]
Notes[modifier | modifier le wikicode]
Quotation to the certain of the euro.
The ECB rate is the reference exchange rate set by the European Central Bank.
The over-the-counter rate is always less favourable than the interbank market rate.
The spread between the ask price and the ask price is the profit margin for commercial banks (transaction cost) and is generally higher for the rarer currencies.
As a result of arbitrage, the direct exchange rates are equivalent to the product of the cross-exchange rates (example: CHF/USD = CHF/EUR ∙ EUR/USD).
Forward transactions are used by economic agents to hedge against the risk of unexpected exchange rate fluctuations. Example of KO players p. 361: a player sold in France for 100 euros and paid 9,000 yen to the Japanese supplier. Compare the gain per player sold in the case of i. immediate payment at the spot exchange rate YEN/EUR = 95.25, ii. future payment at a future spot exchange rate YEN/EUR = 86.95 (yen appreciation), iii. future payment covered by a yen purchase at the forward rate (YEN/EUR) = 93.46].
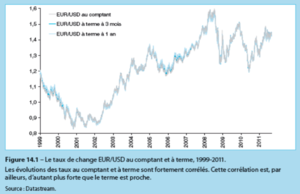
Spot and forward exchange rates[modifier | modifier le wikicode]
Spot and forward exchange rates are closely related (especially as the term approaches).
Forward Contracts and options[modifier | modifier le wikicode]
Currency forwards, futures and options are derivatives, which have grown considerably since the 1970s.
The forward purchase of a currency on the futures market is binding. Once the terms of the contract (amount, maturity) have been agreed, there is no going back even if expectations change. See example on the next page.
In the case of currency forwards (futures), the promise to deliver a given amount of a currency at an agreed term is purchased, and this promise can be resold (realizing a gain or loss in the futures market) at any time. More flexible than the forward, even if the terms of the futures contracts are standardized (= not possible to negotiate the amounts or maturity as in the case of forwards).
Example of forward contracts:
- The Chinese currency (remninbi or Chinese Yuan, CNY) is still non-convertible, i.e. it can only circulate within China and non-residents cannot hold accounts in CNY. How does a US exporting company (which fears a depreciation of the yuan) go about eliminating the exchange rate risk on the 10m of CNY (at a spot rate of 6 CNY/USD) that it will receive in 3 months, knowing that, being the non-convertible currency, it is not possible to use the futures market?
- Solution: the US company enters into a forward contract which consists in paying or receiving the difference, in dollars, compared to the agreed rate (e.g. stability at 6 CNY/USD). For example, if the yuan appreciates to , it will pay m of USD to the People's Bank of China, and, vice versa, it will receive 0.13m of USD from the Chinese central bank if the yuan depreciates to 6.5 CNY/USD → paris.
Typical case where the financial market develops a new instrument to circumvent a (probably transitory) difficulty → creation of a CNY vs. USD forwards market.
Alternative :
A currency option gives the right to buy or sell a specific amount of a currency at a fixed price at any time until the expiration of the specified maturity date (the other party -- seller of the option -- must sell or buy at the discretion of the owner, who in turn has no obligation to actually exercise his right).
Example: You will receive a foreign currency payment on an uncertain date in the next month. To eliminate any risk (of the foreign currency depreciating), you buy a put option that allows you to sell the currency at the fixed rate at any time during the month. In case you need to make a payment you buy a call option.
Demand for foreign currency assets[modifier | modifier le wikicode]
The financial account approach[modifier | modifier le wikicode]
Quotation convention: In the following we will always use the uncertainty quotation (= KO) -> we will always put the national currency in the numerator.
Central idea:
The foreign exchange market is in equilibrium when all assets denominated in all currencies offer the same expected rate of return (non-arbitrage).
, the exchange rate, reflects the price of a (foreign) asset. Asset = transfer of purchasing power in the future. Its current price depends on the anticipation of its future price.
Rating : = anticipated exchange rate (expected, expected). e.g: , -> anticipated appreciation of the USD.
Is it necessary to invest in CHF or in foreign currencies? Capital (en CHF) -> choice:
- If we place in CHF -> interest rate
- If we place in USD -> interest rate
But this information is not enough to make a comparison between the two investments -> calculation of the expected return
Expected rate of return[modifier | modifier le wikicode]
Wealth is held in various forms of assets and transfers purchasing power in the future the desirability of an asset will depend on its rate of return, but the rate of return is rarely known (e.g. the dividend associated with a share might be known, but the value of the security changes over time).
The expected real rate of return is the expected nominal rate of return deflated by a price index. As assets are held in different currencies, they must be expressed in the same currency in order to be comparable.
Other things being equal (which is rarely the case), investors prefer to hold assets with a higher expected real rate of return.
Two other criteria influence the choice of an asset:
- Risk (savers prefer assets with little uncertainty).
- Liquidity (savers prefer more liquid assets).
Hypothesis for the rest: comparable risk and liquidity between securities => we focus on the differences in expected real return, which are closely related to the differences in interest rates between different currencies.
Interest rates[modifier | modifier le wikicode]
Interest rates on different currencies are usually different because they depend on national conditions. On the other hand, when two countries adopt the same currency, such as France and Germany in 1999, interest rates converge and then equalise. (... Is this still true today?)
Expected return on a foreign currency investment ()[modifier | modifier le wikicode]
Hp: the expected return is the only criterion (risk and liquidity are not taken into account).
Investment in USD → 3 transactions:
- USD purchase in → [USD]
- USD investment → [USD]
- sale USD in → [CHF]
Anticipated return on USD :
where
is the anticipated depreciation rate of the CHF.
=>
Approximation[modifier | modifier le wikicode]
If and are low enough, their product can be neglected (e.g: % and % => %) → rule of thumb.
The expected return on the USD then becomes, approximately :
Intuition : . If a depreciation (appreciation) of the national currency is anticipated in the future, this means that when the USD is converted into CHF (at the end of the investment period), a foreign exchange gain (loss) is expected.
On what depends ? Three determinants...
Variation of E[modifier | modifier le wikicode]
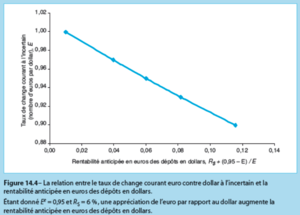
How is it evolving when varies ?
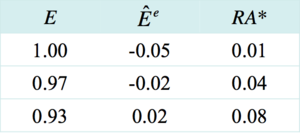
→ Example (table 14.4 of KO) with %, and : the more is low ceteris paribus, the more the is high. Intuition: the cheaper the currency, the higher the expected return on that currency, all other things being equal.
If remains unchanged, as depreciate (appreciation of EUR), the rate of anticipated depreciation increases as well as the :
An appreciation today of the national currency at an anticipated exchange rate () which remains constant implies an expectation of a larger future foreign exchange gain (or a smaller foreign exchange loss) as the expected depreciation margin increases (or the margin of appreciation decreases).
Negative relationship between and . All other things being equal, an appreciation of the national currency (here CHF) increases the AR of a foreign currency investment (here USD).
Influence of on [modifier | modifier le wikicode]
So, in general, if we see today a...
- Appreciation of national currency (↘) ↗ (exchange gain)
- Depreciation of national currency (↗) ↘ (loss on exchange)
The curve describes the evolution of as a function of
Influence of (and ) on [modifier | modifier le wikicode]
If we're expecting a...
- (↘) => ↘ (exchange rate loss)
- Depreciation of national currency () => (exchange rate gain)
- -> in this case: displacement of the whole curve (idem if )
Balance in the foreign exchange market: [modifier | modifier le wikicode]
Equilibrium condition: [modifier | modifier le wikicode]
Assumptions: The agents share the same expectations () and face the same interest rates and exogenous. In the event of an imbalance in the foreign exchange market, it is the spot exchange rate, E, that adjusts.
Intuition: will vary until there is no longer any incentive to change the portfolio allocation between the two currencies = when the expected returns on the two currencies become equal.
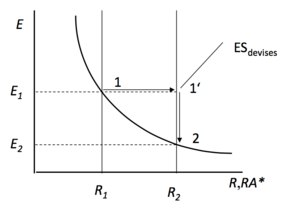
Rating: ED: excess demand; ES: excess supply.
- If => ↗ => ↘ => ↘ = narrows the gap
- If => ↘ => ↗ => ↗ = narrows the gap
Equilibrium for the investor corresponds to a situation of "non-arbitrage" when:
- [1]
= unhedged interest rate parity relationship (), which corresponds to the equilibrium of the foreign exchange market ( adjusts). This relationship gives us a model for determining the spot exchange rate. If we know the interest rate differential and the expected exchange rate we know the spot exchange rate.
Graphical representation of the balance[modifier | modifier le wikicode]
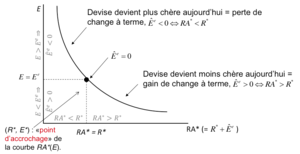
If , the only value of that satisfies the condition is the one that lies vertical to on the curve . Any other value of below or above this curve will lead to an immediate fit of and a return to the curve => equilibrium condition :
The curve , describes the couples (, ) that satisfy the condition of no shading (= ).
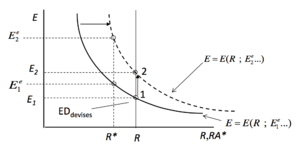
Comparative static: increase in R[modifier | modifier le wikicode]
An increase in the domestic interest rate makes domestic assets more attractive, leading to excess demand for the domestic currency (= ) => appreciation of the domestic currency (↘)
Comparative static: increase of [modifier | modifier le wikicode]
Anticipation that the national currency will depreciate leads agents to reallocate their wealth on foreign currency investments => => the national currency depreciates (↗)
Comparative static: increase of [modifier | modifier le wikicode]
Foreign assets become more attractive => agents will increase their demand for foreign assets => => Domestic currency depreciates (↗)
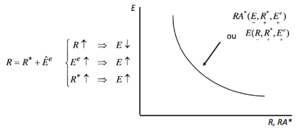
Summary of the [modifier | modifier le wikicode]
Determines the value of E that satisfies the non-arbitration condition. All points along the curve are equilibrium points.
But: on what depends , , ? chap.12-15.
Continuation...[modifier | modifier le wikicode]
The model based on the unhedged interest rate parity represents a first step in determining the exchange rate. We now have to complete it by developing a theory of interest rate formation and expectations.
Empirical verifications[modifier | modifier le wikicode]
Checking the : perfect expectations[modifier | modifier le wikicode]
The condition of is particularly interesting for forecasting purposes. Under the assumption of perfect expectations (), the differential could be used as a prediction of .
Basic idea: if the assumptions underlying the (in particular risk neutrality) are correct and the agents are rational (ie. use all available information and do not make systematic errors), the effective depreciation rate of the national currency, <should be equal to the expected rate of depreciation , (equal to according to the ) plus "white noise": , where is a prediction error of null mathematical expectation.
However, in reality the is very poorly verified, both in terms of the magnitude of the variations and in terms of their direction.
Foreign exchange market efficiency[modifier | modifier le wikicode]
How to interpret this? => foreign exchange market not efficient? If there is a systematic bias in forecasts -> test of market "efficiency", an efficient market is defined as a market where participants are risk neutral and form their expectations in a rational manner [they take into account all the information available to them rather than basing their predictions solely on the past (adaptive expectations)].
If markets are efficient, at any point in time the prices of currencies, or equities, are correctly valued (no over- or underestimation) and price movements will follow a random path.
Econometric tests have shown that markets are not efficient in this sense.
Three possible explanations :
- role of the risk premium ():
- Role of unpredictable events ( news )
- rationality of investors limited?
Risk premium: in this case the forecast bias would come from omitted variables that are to be modeled.
It is likely that the role of "news" (unanticipated events) is a major cause of changes in exchange rate values.
Participants could make systematic errors despite their rationality and learn about market behaviour through a learning process (adaptive expectations) based on the past → unrealistic expectations of future prices (at the origin of the real estate bubble and the last financial crisis).
Summary[modifier | modifier le wikicode]
The financial account approach focuses on the BOP FC as a determinant of the exchange rate (particularly relevant from the 1970s onwards with the gradual liberalisation of the capital market and the growing importance of transaction volumes in the asset market).
There are two exchange rate quotations: the uncertain quotation (= domestic currency units per foreign currency unit) and the certain quotation (foreign currency units per domestic currency unit).
Investment decisions depend (among other things) on the rate of return on assets
The expected rate of return on a foreign currency investment depends on the foreign interest rate and expectations of foreign exchange gains (or losses).
The asset market is in equilibrium when the uncovered interest rate parity condition is verified ()
The spot exchange rate adjusts to ensure equilibrium in the asset market => the can be used to make predictions about the evolution of the exchange rate
A rise in the foreign interest rate, an expected depreciation of the domestic currency or a fall in the domestic interest rate causes an increase in the exchange rate (= depreciation of the domestic currency).
Annexes[modifier | modifier le wikicode]
References[modifier | modifier le wikicode]
- ↑ Page personnelle de Federica Sbergami sur le site de l'Université de Genève
- ↑ Page personnelle de Federica Sbergami sur le site de l'Université de Neuchâtel
- ↑ Page personnelle de Federica Sbergami sur Research Gate
- ↑ Céline Carrère - Faculté d'économie et de management - UNIGE
- ↑ Céline Carrère - Google Scholar Citations
- ↑ Director Céline Carrère - Rectorat - UNIGE
- ↑ Céline Carrère | Sciences Po - Le Laboratoire Interdisciplinaire d'Evaluation des Politiques Publiques (LIEPP)
- ↑ Céline Carrere - EconPapers
- ↑ Céline Carrère's research works - ResearchGate