« Los costos de producción » : différence entre les versions
Aucun résumé des modifications |
Aucun résumé des modifications |
||
| Ligne 29 : | Ligne 29 : | ||
}} | }} | ||
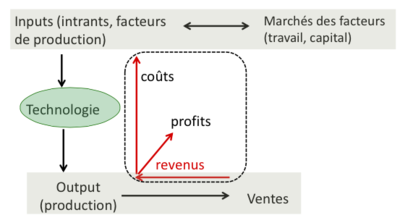
Es la parte de la microeconomía llamada Organización Industrial. | |||
El análisis de costos es un paso analítico esencial porque el objetivo de cualquier agente económico, especialmente para las empresas, es maximizar los beneficios. | |||
Su objetivo es comprender el comportamiento de las empresas en diversas condiciones de mercado (competencia perfecta y diferentes formas de competencia imperfecta). | |||
Los costos son los principales determinantes que influyen en las decisiones de producción y en los precios. En otras palabras, el programa de la empresa depende de la elección de los factores de producción. | |||
El objetivo final de las empresas es maximizar los beneficios. Los costos de producción, que influyen en la función de suministro, son importantes determinantes de los beneficios. | |||
* | *El "beneficio de las empresas" está dado por: | ||
: | :Beneficio = (Ingresos totales) - (Costo total) | ||
:<math>\pi = RT - CT</math> | :<math>\pi = RT - CT</math> | ||
* | *El "ingreso total" (RT) está dado por: | ||
: | :Receta total = Precio * (Cantidad vendida) | ||
El resto de este capítulo está dedicado al análisis de los costos de producción. | |||
Esta teoría está detrás de la función de suministro del mercado, la función de suministro es una función creciente. Sin embargo, no hemos justificado cuál es el comportamiento de las empresas. La idea es justificar el comportamiento de la función de suministro. | |||
Con la teoría del consumo analizaremos todo lo que hay detrás de la función de demanda. | |||
[[Fichier:Une entreprise simplifiée 1.png|400px|vignette|centré|Une entreprise simplifiée.]] | [[Fichier:Une entreprise simplifiée 1.png|400px|vignette|centré|Une entreprise simplifiée.]] | ||
| Ligne 59 : | Ligne 59 : | ||
}} | }} | ||
= | = Función de producción y costos totales = | ||
== ¿Cuál es el costo de producción? == | |||
El segundo principio económico enunciado en la primera sesión nos dice que el costo de algo no sólo es igual al pago monetario, sino también al valor de lo que uno tiene que renunciar para adquirirlo. | |||
Esto se llama el costo de oportunidad. La noción de costo en términos económicos | |||
está vinculado al concepto de costo de oportunidad. | |||
Cuando una empresa produce un bien, se enfrenta..: | |||
* | *Costes explícitos que se dan por los pagos monetarios, estos son flujos de salida (enfoque contable). | ||
* | * costes implícitos que vienen dados por el valor de lo que ha tenido que renunciar; se trata de costes que no tienen una contrapartida monetaria inmediata (enfoque económico). | ||
Ejemplos de costos implícitos: | |||
* | *el costo del capital invertido en la empresa (y que podría haber sido invertido en otro lugar); | ||
* | *el salario que el empresario recibiría como empleado en otra actividad. | ||
El contable no tiene en cuenta los costos implícitos al evaluar los costos de producción y el beneficio contable de la empresa. El economista, en cambio, tiene en cuenta los costos explícitos e implícitos. | |||
== Profit économique et profit comptable == | == Profit économique et profit comptable == | ||
| Ligne 83 : | Ligne 83 : | ||
[[Fichier:Profit économique et profit comptable 1.png|400px|vignette|centré]] | [[Fichier:Profit économique et profit comptable 1.png|400px|vignette|centré]] | ||
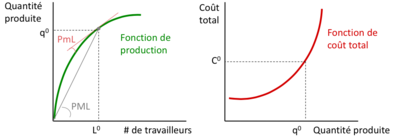
== La | == La función de producción y los costos totales == | ||
La | La función de producción muestra la relación técnica entre la cantidad producida (q) y la cantidad de insumos utilizados para producir esa cantidad. | ||
La | La función de costo total muestra la relación entre la cantidad de producción (q) y su costo de producción. | ||
Las dos funciones están estrechamente relacionadas: los costos totales están determinados por las limitaciones técnicas de la función de producción. | |||
[[Fichier:Fonction de production et les coûts totaux 1.png|400px|vignette|centré]] | [[Fichier:Fonction de production et les coûts totaux 1.png|400px|vignette|centré]] | ||
== | == Producto laboral marginal y medio == | ||
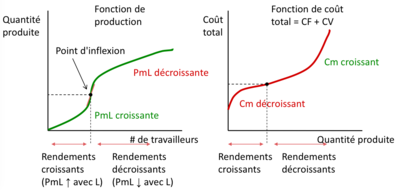
El producto laboral marginal, o productividad laboral marginal, es la cantidad de producción adicional que se puede producir con una unidad adicional de este insumo: | |||
:::PmL = aumento de la producción/trabajo adicional = <math>\frac {\Delta q}{\Delta L}</math> o, para variaciones muy pequeñas, <math>PmL = \frac {\partial q}{\partial L}</math>. | |||
Por lo tanto, está dada por la pendiente de la función de producción. | |||
La función de producción anterior muestra una PmL decreciente: la pendiente se hace cada vez más pequeña a medida que se aumentan las cantidades producidas → una unidad de trabajo adicional aumenta la producción, sí, pero en una cantidad cada vez menor. | |||
: | La producción laboral media, o productividad laboral media, mide la cantidad que cada trabajador produce en promedio: | ||
:::PML = producción total/# trabajadores = <math>\frac {q}{L}</math>. | |||
Por lo tanto, está dada por la pendiente del radio que sale del origen. | |||
== Los rendimientos decrecientes == | |||
Hablamos en este caso de la LEY DE LOS RENDIMIENTOS MARGINALES DE CRECIMIENTO = dado el resto de los insumos, la productividad laboral disminuye con la cantidad de trabajo. | |||
Intuición: cuando los otros insumos son fijos, añadir trabajadores adicionales no puede aumentar la producción proporcionalmente. | |||
Ejemplo: en una oficina, los trabajadores empiezan a sentirse cohibidos y se turnan en una computadora o fotocopiadora con expectativas y problemas de coordinación. | |||
Esto da lugar a una función de producción con una pendiente cada vez menor y una función de costo total con una pendiente cada vez mayor a medida que aumentan las cantidades de producción. | |||
== | Intuición: si se necesitan más y más trabajadores para producir una unidad adicional, los costos de producción de esta unidad adicional tendrán que aumentar => el costo aumenta a un ritmo creciente. | ||
[[Fichier:Exemple fonction de production et coût total 1.png|400px|vignette|centré| | |||
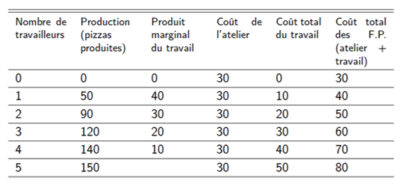
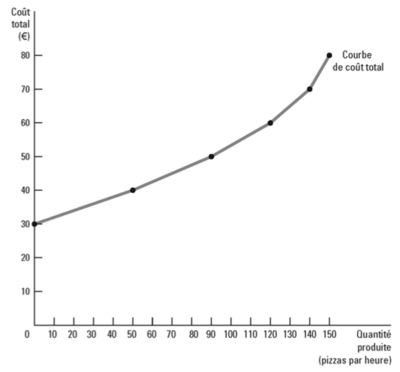
== Ejemplo: función de producción y costo total == | |||
[[Fichier:Exemple fonction de production et coût total 1.png|400px|vignette|centré|La producción y la función de coste total de un productor de pizzas.]] | |||
<gallery> | <gallery> | ||
Exemple fonction de production et coût total 2.png| | Exemple fonction de production et coût total 2.png|Función de producción. | ||
Exemple fonction de production et coût total 3.png| | Exemple fonction de production et coût total 3.png|Curva de costo total. | ||
</gallery> | </gallery> | ||
= | = Diferentes medidas de costos = | ||
== | == Diferentes medidas de costos== | ||
Coûts fixes (CF) sont les coûts qui ne varient pas avec la quantité produite (liés aux investissements en capital physique). | Coûts fixes (CF) sont les coûts qui ne varient pas avec la quantité produite (liés aux investissements en capital physique). | ||
Version du 28 mars 2020 à 19:15
| Professeur(s) | |
|---|---|
| Cours | Introducción a la microeconomía |
Lectures
- Introducción al curso de Introducción a la Microeconomía
- Enfoque metodológico en el curso introductorio de microeconomía
- Fuerzas del mercado: oferta y demanda
- La elasticidad y sus aplicaciones
- Oferta, demanda y políticas gubernamentales
- Excedente del consumidor y del productor
- Las externalidades y el papel del Estado
- Los bienes públicos
- Los costos de producción
- Las empresas en perfecta competencia
- Las compañías de monopolio
- Competencia monopólica
- Oligopolio
- Limitaciones y preferencias del consumidor
- Elección del consumidor
- Problemas de información y elecciones públicas
Es la parte de la microeconomía llamada Organización Industrial.
El análisis de costos es un paso analítico esencial porque el objetivo de cualquier agente económico, especialmente para las empresas, es maximizar los beneficios.
Su objetivo es comprender el comportamiento de las empresas en diversas condiciones de mercado (competencia perfecta y diferentes formas de competencia imperfecta).
Los costos son los principales determinantes que influyen en las decisiones de producción y en los precios. En otras palabras, el programa de la empresa depende de la elección de los factores de producción.
El objetivo final de las empresas es maximizar los beneficios. Los costos de producción, que influyen en la función de suministro, son importantes determinantes de los beneficios.
- El "beneficio de las empresas" está dado por:
- Beneficio = (Ingresos totales) - (Costo total)
- El "ingreso total" (RT) está dado por:
- Receta total = Precio * (Cantidad vendida)
El resto de este capítulo está dedicado al análisis de los costos de producción.
Esta teoría está detrás de la función de suministro del mercado, la función de suministro es una función creciente. Sin embargo, no hemos justificado cuál es el comportamiento de las empresas. La idea es justificar el comportamiento de la función de suministro.
Con la teoría del consumo analizaremos todo lo que hay detrás de la función de demanda.
Función de producción y costos totales
¿Cuál es el costo de producción?
El segundo principio económico enunciado en la primera sesión nos dice que el costo de algo no sólo es igual al pago monetario, sino también al valor de lo que uno tiene que renunciar para adquirirlo.
Esto se llama el costo de oportunidad. La noción de costo en términos económicos está vinculado al concepto de costo de oportunidad.
Cuando una empresa produce un bien, se enfrenta..:
- Costes explícitos que se dan por los pagos monetarios, estos son flujos de salida (enfoque contable).
- costes implícitos que vienen dados por el valor de lo que ha tenido que renunciar; se trata de costes que no tienen una contrapartida monetaria inmediata (enfoque económico).
Ejemplos de costos implícitos:
- el costo del capital invertido en la empresa (y que podría haber sido invertido en otro lugar);
- el salario que el empresario recibiría como empleado en otra actividad.
El contable no tiene en cuenta los costos implícitos al evaluar los costos de producción y el beneficio contable de la empresa. El economista, en cambio, tiene en cuenta los costos explícitos e implícitos.
Profit économique et profit comptable
Le profit économique ne peut jamais être plus grand que le profit comptable et un profit comptable positif est compatible avec une entreprise qui fait des profits économiques nuls.
La función de producción y los costos totales
La función de producción muestra la relación técnica entre la cantidad producida (q) y la cantidad de insumos utilizados para producir esa cantidad.
La función de costo total muestra la relación entre la cantidad de producción (q) y su costo de producción.
Las dos funciones están estrechamente relacionadas: los costos totales están determinados por las limitaciones técnicas de la función de producción.
Producto laboral marginal y medio
El producto laboral marginal, o productividad laboral marginal, es la cantidad de producción adicional que se puede producir con una unidad adicional de este insumo:
- PmL = aumento de la producción/trabajo adicional = o, para variaciones muy pequeñas, .
Por lo tanto, está dada por la pendiente de la función de producción.
La función de producción anterior muestra una PmL decreciente: la pendiente se hace cada vez más pequeña a medida que se aumentan las cantidades producidas → una unidad de trabajo adicional aumenta la producción, sí, pero en una cantidad cada vez menor.
La producción laboral media, o productividad laboral media, mide la cantidad que cada trabajador produce en promedio:
- PML = producción total/# trabajadores = .
Por lo tanto, está dada por la pendiente del radio que sale del origen.
Los rendimientos decrecientes
Hablamos en este caso de la LEY DE LOS RENDIMIENTOS MARGINALES DE CRECIMIENTO = dado el resto de los insumos, la productividad laboral disminuye con la cantidad de trabajo.
Intuición: cuando los otros insumos son fijos, añadir trabajadores adicionales no puede aumentar la producción proporcionalmente.
Ejemplo: en una oficina, los trabajadores empiezan a sentirse cohibidos y se turnan en una computadora o fotocopiadora con expectativas y problemas de coordinación.
Esto da lugar a una función de producción con una pendiente cada vez menor y una función de costo total con una pendiente cada vez mayor a medida que aumentan las cantidades de producción.
Intuición: si se necesitan más y más trabajadores para producir una unidad adicional, los costos de producción de esta unidad adicional tendrán que aumentar => el costo aumenta a un ritmo creciente.
Ejemplo: función de producción y costo total
Diferentes medidas de costos
Diferentes medidas de costos
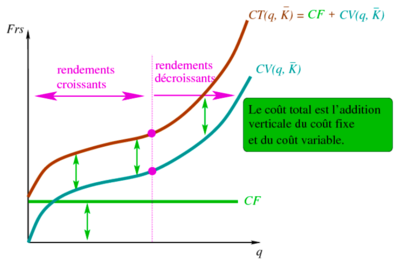
Coûts fixes (CF) sont les coûts qui ne varient pas avec la quantité produite (liés aux investissements en capital physique).
Coûts variables (CV) sont les coûts qui varient avec la quantité produite (liés à la rémunération des travailleurs au d'autres inputs variables).
Coût total (CT) est la somme du coût fixe et coût variable :
- .
Coût moyen (CM) est le coût total par unité produite et donc :
=coût moyen = coût fixe moyen + coût variable moyen
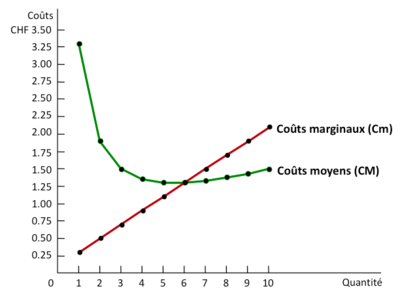
Coût marginal (Cm) est l’augmentation dans le coût total associée à la production d’une unité additionnelle du bien final (= pente de la fonction de coût total)
- Cm = (variation dans le coût total)/(variation des quantités)
- (ou = pour des variations infinitésimales).
Exemple
Exemple : coût total
Exemple : coût marginal
Le coût marginal généralement augmente avec la quantité produite à cause de la productivité décroissante qui rend la production d’une unité supplémentaire de plus en plus coûteuse. Le CF ne variant pas, par définition, avec la quantité produite, le Cm indique nécessairement la variation du CV.
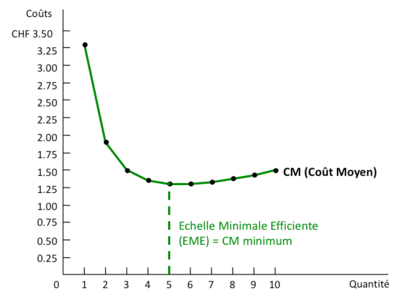
Exemple : Coût moyen
Le coût moyen a généralement une forme en U, c’est-à- dire il diminue avec les quantités produites lorsqu’on commence à produire le bien (le CF est réparti sur un petit nombre d'unités seulement), mais pour des quantités plus grandes de production il augmente avec les quantités produites (à cause de l'incidence grandissante du CVM).
Coût marginal et coût moyen
Lorsque le coût marginal est supérieur au coût moyen, le coût moyen est croissant, alors qu’il est décroissant si le coût marginal lui est inférieur => Le coût marginal rencontre le coût moyen au minimum du coût moyen (EME).
Coût moyens (fixe et variable)
Plus en général
La productivité marginale est initialement croissante (spécialisation des travailleurs dans leurs tâches) et décroissante ensuite (car les facteurs fixes doivent être partagés par un nombre croissant de travailleurs)
Propriétés
Trois propriétés importantes des fonctions de coûts :
- Le coût marginal va, tôt ou tard, finir par augmenter avec la quantité produite.
- Le coût moyen a donc une forme en U (si le coût marginal était toujours décroissant on aurait des coûts moyens toujours décroissant également).
- Le coût marginal croise la fonction de coût moyen à son minimum (ou à l’échelle minimale efficiente).
Résumé graphique
Exemple numérique
Une entreprise manufacturière a le coût total suivant :
Lien entre fonction de production et coûts
La fonction de coût total est une sorte de fonction de production lue "à l'envers" (fonction réciproque):
Étant donné un certain stock de capital physique, on détermine quel est le nombre d'heures de travail nécessaires pour produire une certaine quantité q (= "envers" de la fonction de production);
On multiple ces heures de travail par le salaire horaire et on détermine ainsi la masse salariale 𝑤 ∙ 𝐿(𝐾, 𝑞) (= CV, si L est le seul input variable);
On rajoute à cela le coût fixe engendré par le capital physique pour obtenir le coût total.
Court versus long terme
Fonction de production de court et de long terme
Toute l'analyse qui précède a été faite en faisant implicitement l'hypothèse qu'un seul facteur de production, le travail, pouvait être adapté par l'entreprise afin de réaliser ses décisions de production. Ceci revient à dire que nous avons fait implicitement l'hypothèse que tous les inputs sauf le travail sont fixes. Autrement dit, nous avons fait une analyse de court terme.
Hypothèse : pour produire une certaine quantité q du bien, la firme utilise deux(mais on pourrait en considérer plus) inputs de production :
- le capital physique,
- le travail,
L’entreprise peut choisir différentes combinaisons de capital et de travail qui conduiront à différents niveau de production. La maximisation du profit sera maintenant une maximisation sur les deux quantités et .
Pour beaucoup de firmes, la répartition du coût total entre coûts fixes et coûts variables dépend de l’horizon temporel.
- COURT TERME
Une entreprise qui doit décider au jour le jour quelle quantité produire considère sa capacité de production (= locaux, machines, instruments… = capital physique) comme donnée → fonction de production: .
- LONG TERME
Quand elle planifie son activité future, l'entreprise peut décider de sa capacité de production → tous les inputs sont flexibles →fonction de production: .
Coûts de production dans le court et long terme
Les coûts fixes sont liés au long terme ; les coûts variables sont des coûts modifiables sur le court terme.
La distinction entre coût variable et coût fixe dépend de l’horizon de temps qu’on considère:
- dans le court terme certains coûts sont fixes (en général, les coûts liés au capital physique). On doit utiliser un stock de capital fixe
- dans le long terme on peut rendre les coûts fixes variables notamment grâce aux investissements.
- mais avec le temps ces mêmes coûts fixes deviennent variables car les entreprises peuvent ajuster leurs décisions sur tous les inputs (modification de la capacité physique de production).
Comme beaucoup de décisions sont fixes dans le court terme mais variables dans le long terme les fonctions de coût des entreprises ne sont pas les mêmes dans le court terme et dans le long terme.
Parce que beaucoup de décisions sont fixes dans le court terme mais variables dans le long terme, les coûts d’une firme sur le long terme diffèrent des coûts dans le court terme.
Il sera toujours plus facile d’avoir des coûts de production plus petits dans le long terme car on peut ajuster les facteurs de production qui sont fixes dans le court terme.
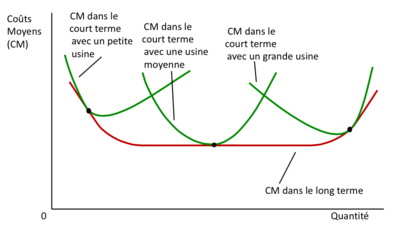
Les coûts moyens dans le court et long terme
Economies d’échelle
La pente de la fonction de CM à long terme nous indique la présence ou absence d’économies d’échelle.
Rendements marginaux vs rendements d'échelle
Ne pas confondre le concept de rendement marginal ou de produit marginal avec le concept de rendement d'échelle!
- Le rendement marginal (souvent décroissant) est un concept de court terme: il nous indique la variation de l'output pour un changement d'un seul input, tous les autres étant fixes.
- Le rendement d'échelle (croissant, constant, décroissant) est un concept de long terme : tous les inputs sont variables et une entreprise qui veut modifier ses décisions de production peut aussi intervenir sur sa capacité de production.
Intuition pour économies d'échelle (→ rendements d'échelle croissants) :
- dans une usine plus grande beaucoup de tâches peuvent être agrégées + spécialisation plus élevée de K et de L possible + possibilité d’utiliser de la main d’œuvre qualifiée ou des machines plus performantes...
Intuition pour déséconomies d'échelle (→ rendements d'échelle décroissants) :
- difficultés croissantes dans l’organisation et l’intégration des activités dans une usine de taille grandissante + moins d’engagement personnel des travailleurs + le management ne suit pas (sorte de « facteur fixe »)...
Résumé
L’objectif de l’entreprise est de maximiser le profit = différence entre la recette totale et le coût total.
Le coût total inclut les coûts explicites mais aussi les coûts implicites (= coûts d'opportunité de la production).
Le coût total de l’entreprise est un reflet de sa fonction de production.
Une fonction de production type montre généralement une productivité décroissante (en tout cas a partir d’une certaine quantité ou échelle de production).
Le coût total de l’entreprise est divisé entre les coûts fixes (qui ne changent pas avec la quantité produite) et les coûts variables (qui dépendent des quantités produites).
Le coût moyen est le coût total par unité produite.
Le coût marginal nous donne l’augmentation dans le coût total nécessaire à produire une unité additionnelle. Généralement augmente avec la quantité produite (en tout cas a partir d’une certaine quantité produite).
Si le coût marginal est croissant, le coût moyen doit, tôt ou tard, commencer à augmenter; il va donc d’abord diminuer et ensuite augmenter avec les quantités produites. Il aura une forme en U.
La courbe de coût marginal croise la fonction de coût moyen à son minimum (au point d’échelle minimum efficace).
La forme des fonctions de coût dépend de l’horizon de temps qu’on considère.
Beaucoup de coûts qui sont fixes dans le court terme deviennent variables dans le long terme.