Le traitement des données
| Faculté | Faculté des sciences de la société |
|---|---|
| Département | Département de science politique et relations internationales |
| Professeur(s) | Marco Giugni[1] |
| Cours | Introduction aux méthodes de la science-politique |
Lectures
L’analyse des données quantitatives est très différente de l’analyse des données qualitatives ; ce sont deux pratiques de la recherche très différentes, voire même opposées.
Nous allons nous focaliser sur l’analyse quantitative qui est en fait plus facile que l’analyse des données qualitative ne serait-ce parce qu’il y a des routines institutionnalisées.
Matrice des données[modifier | modifier le wikicode]
C’est une matrice qui croise les cas étudiés avec un certain nombre de variables à savoir les variables en colonne et les cas en ligne.
Il faut attribuer un code qui permette d’exclure de l’analyse ceux qui n’ont pas répondu et les différencier de ceux qui ont répondu.
Il y a trois analyses qui correspondent à trois objectifs différents :
- analyses univariées : analyses qui se font sur une seule variable ou une seule caractéristique.
- analyses bivariées : mise en relation de deux variables, on veut croiser des données pour analyser les variations plus subtilement comme l’intérêt de la politique selon la ville ou l’âge.
- analyses multivariées : on pense qu’un phénomène expliqué n’est jamais expliqué par une seule variable indépendante ; d’autre part on veut introduire des contrôles afin de contrôler les relations à travers la technique de la dépuration.
Il faut faire une distinction entre une analyse descriptive qui veut décrire un « état de fait » que l’on fait univariée ou bivariée.
Types d’analyses univariées[modifier | modifier le wikicode]
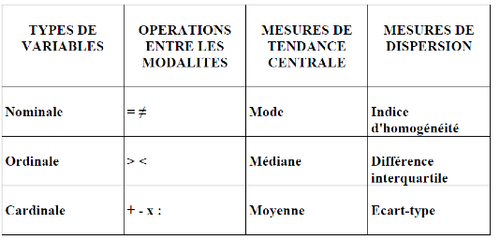
Types de variables et opérations entre modalités[modifier | modifier le wikicode]
Il y a différents types d’analyses univariées, ces techniques dépendent du type de variable :
- variables nominales : on peut faire seulement des opérations d’équivalence ou de différence.
- variables ordinales : permet d’ordonner c’est-à-dire catégoriser selon un ordre du plus petit au plus grand.
Nota bene : les variables ordinales et cardinales sont catégorielles, relevant de données discrètes, on ne peut voir les distances.
- variables cardinales : permettent en plus des opérations précédentes de faire les quatre opérations arithmétiques de base.
Mesure de tendance centrale[modifier | modifier le wikicode]
Lorsqu’on fait une analyse quantitative, il faut s’interroger sur le type de variables et ensuite on choisit l’outil à utiliser. On peut distinguer entre deux grands types de mesures c’est-à-dire entre deux types d’informations qu’on veut avoir des variables uniques :
- mesures de tendance centrale
- mesures de dispersion.
Nota bene : selon la variable les mesures sont différentes.
La moyenne est une mesure de valeur de tendance centrale que l’on peut appliquer aux variables cardinales, mais on ne peut l’appliquer aux variables catégorielles. La médiane est la catégorie qui sépare la série statistique en deux avec un même nombre de cas d’un côté et de l’autre.
Ce sont des informations importantes qui forment le point de départ de ce type de description des données permettant de savoir quoi faire ensuite dans le cas d’analyses plus sophistiquées
Mesure de dispersions[modifier | modifier le wikicode]
On distingue aussi des mesures de dispersions : la mesure de base est l’écart-type qui est une mesure standardisée qui varie de -1 à +1 de la variance qui est la mesure qui indique de quelle manière sont distribués les individus.
La variance est très importante pour calculer la probabilité d’erreur. Il faut différentes mesures selon l’unité de mesure de la variable et il faut tenir compte de la mesure de tendance centrale et de dispersion comme l’écart-type qui est le coefficient clef dans toute l’analyse quantitative.
Types d’analyses bivariées[modifier | modifier le wikicode]
Dans ce cadre on souhaite croiser des caractéristiques soit dans une optique descriptive soit dans une optique explicative. En fonction du type de variable, on a des techniques différentes pour analyser et traiter les données.
Il faut s’intéresser à la fois aux variables dépendantes et aux variables indépendantes. En croisant, il faut regarder du côté de la variable dépendante et indépendante si on a affaire à des variables catégorielles ou ordinales permettant de distinguer trois grandes familles de types d’analyses :
- variables catégorielles / nominale - nominale : on fait des tableaux de contingence, on ne peut utiliser les autres techniques. La plupart du temps en science politique on a affaire à ce type de variables, car les réponses donnent lieu à des variables ordinales. Il y a des coefficients qui permettent de donner une mesure unique de la relation entre ces deux variables comme le V de Cramer qui permet de voir l’association entre variables catégorielles. Pour interpréter, il est important que le pourcentage total doit toujours se référer aux catégories de la variable indépendante ; on veut voir comment la distribution sur la variable dépendante dépend des fonctions dans la variable indépendante. L’indication du nombre de cas permet de voir si le processus est statistiquement représentatif, car la taille de l’échantillon affecte la mesure.
- variables cardinales - cardinales: on ne fait plus un tableau croisé, on à d’autres outils et en particulier l’outil de la régression et de la corrélation :
- covariation : lorsqu’on a deux variables continues, lorsqu’une augmente l’autre augmente de manière proportionnelle ou inversement proportionnelle, les deux variables sont liées dans ce sens.
- corrélation : c’est simplement une covariation standardisée c’est-à-dire qui se situe entre -1 et +1. On standardise pour faire en sorte de comparer des variables qui à la base sont mesurées de manière différente ; si on a par exemple des échelles de 0 à 10 et des échelles allant de 0 à 5 on ne peut comparer ces variables alors il faut faire en sorte de standardiser ces informations. On peut reconduire les variables sur la même échelle ou un logiciel qui calcule une corrélation standardisée.
- régression : dans une corrélation on est dans une optique descriptive, on ne cherche pas à voir une direction de la causalité dans une régression on veut voir si deux variables sont associées, liées, corrélées.
- variables indépendantes nominales – variables dépendantes cardinales : on ne peut appliquer les tableaux croisés ni les corrélations et régressions ; on fait une analyse de la variance ou de la covariance dont le cas le plus simple est une comparaison de moyennes qui pourrait par exemple être le nombre de fois que les individus participent à une élection en fonction du canton.
Régression linéaire[modifier | modifier le wikicode]
C’est un ensemble très varié et parfois complexe d’outils, mais c’est l’outil principal. La régression linéaire est l’élément principal ; une bonne partie des analyses quantitatives faites en science sociale s’appuient sur la régression linéaire.
On parle de linéarité, car on postule qu’il y a une relation linéaire entre les variables qu’on étudie, en d’autres termes il y a une fonction linéaire derrière cette relation ; cependant, on peut aussi envisager des régressions qui ne sont pas que linéaires.
On présuppose que ce qu’on veut expliquer est une fonction linéaire d’une ou plusieurs variables indépendantes. Cela est crucial, car la régression linéaire n’est qu’un sous-ensemble d’une famille plus large d’analyses de régressions qui ne se base pas sur une idée de linéarité entre les deux variables.
Le modèle le plus simple est avec une variable explicative comme, par exemple, la participation politique en fonction de l’intérêt pour la politique.
En terme descriptif il y a une forte corrélation entre ces deux variables ; si une hypothèse dit que c’est l’intérêt pour la politique qui influence la participation alors on fait une analyse de régression.
On a toujours le problème de l’endogénéité dans ce type d’analyse, on postule que l’intérêt pour la politique détermine une participation ; on pourrait aussi postuler que plus on participe plus on développe un intérêt pour la politique.
La participation politique est une fonction linéaire de l’intérêt pour la politique « plus » un facteur constant à savoir la valeur de Y lorsque X est égal à 0 c’est-à-dire quel est mon niveau de participation lorsque l’intérêt pour la politique est nul. Au fond c’est où la droite de régression croise l’axe des ordonnées.
Dans l’analyse multivariée, il y a toujours une marge d’erreur ; une chose est liée si on des données du sondage liées à la marge d’erreur entre population et échantillon, mais indépendamment qu’on soit en train de travailler sur des échantillons ou une population globale ; il y a un terme d’erreur qui intervient, car il y a toujours quelque chose qui influence ce qu’on veut expliquer et qui n’est pas inclus dans le modèle de régression comme, par exemple, l’éducation, l’âge, le contexte social, institutionnel, etc.
En fait, le E regroupe la variance non expliquée à savoir tout ce qui pourrait expliquer Y, mais n’est pas introduit dans le modèle, c’est le problème de la sous-spécification du modèle à savoir l’enjeu concernant la spécification du modèle ; plus un modèle a plus de variables plus il risque d’être sous-spécifié et moins on explique de variations dans le Y et plus le E en termes d’erreur est élevé, on veut réduire au maximum le E.
Ceci permet de dire que le fait de ne pas inclure certaines variables dans un modèle explicatif à deux conséquences majeures :
- le modèle est sous-spécifié, on explique peu la variabilité de Y avec ce modèle c’est-à-dire les facteurs fortement corrélés avec ce que l’on souhaite étudier.
- la deuxième raison est liée au contrôle des variables, car si on introduit l’intérêt pour la politique, une troisième variable peut influencer l’intérêt pour la politique et la participation pour la politique ; l’association est fallacieuse.
On veut inclure le maximum de variables dont on pense qu’elle peut influencer directement Y ou indirectement faisant que la relation entre X et Y soit fausse ou seulement apparente.
Le B est le coefficient de régression à savoir la pente de la droite de régression donnant la force de l’effet du X car il est multiplicatif par X c’est-à-dire que plus l’effet de X est fort plus B est élevé.
Le B peut être non standardisé ou standardisé. « Standardisation » signifie normaliser et le but est de pouvoir comparer des coefficients différents.
On est dans une logique additive, il y a des « + » ; on suppose que la variation de Y est une fonction linéaire est additive ou cumulée de l’effet de toutes les autres variables introduites dans le modèle.
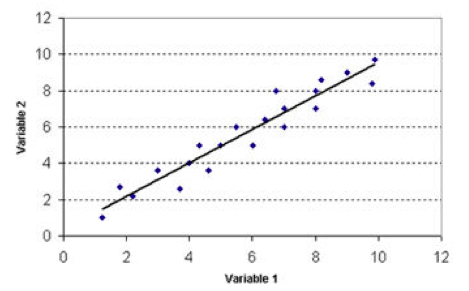
Droite de régression[modifier | modifier le wikicode]
La droite de régression représente la fonction de régression linéaire. On veut regarder de combien augmente Y lorsqu’on augmente X. admettons que les (0 ; 12) sont l’intérêt pour la politique et l’autre la participation politique; on peut voir qu’il y a une corrélation assez forte entre les deux, lorsqu’on a une augmentation de l’intérêt pour la politique on augmente la participation politique.
Les points bleus représentent les cas, la droite de régression est l’estimation des valeurs et donc on va regarder dans quelle mesure et comment cette droite rencontre un nuage de points.
La qualité du modèle a à voir à la qualité de l’estimation qui dépend beaucoup de la manière dont sont distribués les points. Il est possible que le nuage de point soit estimé pour une droite qui a la même pente, toutefois la qualité de cet effet est le même alors qu’il est diffèrent parce que la droite ne fait qu’une approximation beaucoup plus précise du nuage de points ou les points sont proches de la droite.
Il faut retenir que l’un des principaux instruments privilégiés pour l’analyse quantitative lorsqu’on a à faire à des variables intervalles ou cardinal et l’analyse de la corrélation ou de la régression.
L’idée de la régression linéaire qui est un sous-ensemble d’un ensemble plus vaste se base sur l’idée d’une fonction linéaire entre X et Y ; on essaie d’estimer un nuage de points qui représente le croisement entre les deux variables dans l’échantillon donc on va analyser la droite de régression et sa pente. Si la pente est de 0 alors Y ne change pas quand on change X, on peut être très intéressé à la politique, mais on y participe toujours au même niveau.
Analyses multivariées[modifier | modifier le wikicode]
Analyse de régression[modifier | modifier le wikicode]
Selon le type de variables que l’on souhaite expliquer, on peut ou on ne peut pas appliquer l’outil de régression linéaire, il y a par exemple la régression logistique dans le cas de variables dummies soit absence ou présence, on ne peut appliquer la régression linéaire, car les présupposés de base ne sont pas garantis.
Analyse des chemins causaux (path analysis)[modifier | modifier le wikicode]
Un des problèmes de l’analyse de la régression est qu’on suppose que Y est une fonction linéaire de la somme de toutes les variables indépendantes or se faisant on regarde que les effets directs des variables d’un modèle ; toutefois que se passe-t-il lorsqu’on veut regarder des effets indirects ?
On fait une analyse des « chemins causaux » ; il y a des coefficients de régression qui peuvent être significatif ou pas, mais on peut voir des chemins causaux c’est-à-dire qu’on peut voir de quelle manière les valeurs de gauche influence la participation non pas directement, mais indirectement à savoir que le fait d’être de gauche fait qu’on a plus de probabilités d’être intégré dans certains types de réseau développent un internet pour un certain enjeu qui permet de développer un sentiment d’efficacité individuel faisant qu’on a une intensité plus forte de participation. On introduit des variables intermédiaires.
Au lieu d’avoir une indication, on en a plusieurs parce que chaque variable peut ou est une variable dépendante, on fait une somme d’équations.
Analyse factorielle[modifier | modifier le wikicode]
C’est une analyse qui a pour objectif de réduire la complexité qu’on peut avoir lorsqu’on a une matrice de données avec beaucoup de variables et de cas et que l’on veut avoir un index plus succinct.
Lorsqu’on a parlé d’opérationnalisation des concepts complexes, on est arrivé à une dernière étape de construction ; l’analyse factorielle permet de construire des index par l’analyse des liens sous-jacents qui expliquent la variation sur un ensemble multiple d’indicateurs.
C’est un outil fréquemment utilisé en science politique et notamment lorsqu’on étudie les changements de valeurs.
Analyse multiniveaux[modifier | modifier le wikicode]
Auparavant toutes les mesures concernaient les variables individuelles, maintenant il y a des propriétés du contexte qui ne sont pas de l’individu qui peuvent influencer la participation politique comme le système électoral ou le type de système politique.
Dans une optique de régression normale il y a des manières de court-circuiter le problème, on ne peut intégrer les facteurs contextuels dans l’analyse on peut simplement comparer.
L’analyse multiniveau permet de faire une analyse de régression multiniveau, on ajoute des propriétés du contexte et pas seulement des propriétés individuelles ; on intègre des propriétés individuelles et contextuelles. Il y a ce développement important en sciences politiques.
Type de méthodes qualitatives[modifier | modifier le wikicode]
On peut faire une distinction entre l’analyse de contenu et l’analyse de discours. Ces termes ne font pas le consensus dans la littérature, certains estiment que l’analyse de discours est un type d’analyse de contenu et pour d’autres ce n’est pas le cas.
Analyse de contenu[modifier | modifier le wikicode]
L’analyse de contenu s’intéresse au poids, elle est plus descriptive, elle s’intéresse aux différents enjeux soulevés par des personnes. On peut faire une distinction ultérieure :
- thématique : on compte le nombre de fois qu’un tel thème apparaît dans un discours.
- lexicale : analyse basée sur l’analyse des occurrences ou cooccurrences à savoir une analyse qualitative qui a des éléments d’analyse quantitative.
Analyse de discours[modifier | modifier le wikicode]
C’est une analyse interprétative, on parle d’une famille de techniques, on peut dire qu’on s’intéresse à comment et aux effets d’un discours donné.
Pour simplifier, l‘analyse de contenu est plutôt descriptive et l’analyse de discours explicatif.
Étapes de l’analyse thématique[modifier | modifier le wikicode]
Il y a cinq grandes étapes :
- familiarisation (préanalyse) : il faut d’abord se familiariser avec le matériel à disposition.
- identification d’un cadre thématique (schéma de codage, index) : manière de coder l’information soit d’identifier le cadre thématique.
- indexation (codage) : réduire l’information.
- cartographie (catégorisation et réduction des données) : création de typologies, de classifications, réduction des données afin de pouvoir les interpréter.
- mapping et interprétation (analyse et interprétation)
Étapes de l’analyse de discours[modifier | modifier le wikicode]
- Préanalyse
- Identification d'éléments pertinents
- Analyse systématique à partir des éléments identifiés