The processing of data
| Faculté | Faculté des sciences de la société |
|---|---|
| Département | Département de science politique et relations internationales |
| Professeur(s) | Marco Giugni[1] |
| Cours | Introduction to the methods of political science |
Lectures
The analysis of quantitative data is very different from the analysis of qualitative data; they are two very different or even opposed research practices.
We will focus on quantitative analysis, which is in fact easier than the analysis of qualitative data, if only because there are institutionalized routines.
Data matrix[modifier | modifier le wikicode]
It is a matrix that cross-references the cases studied with a number of variables, namely column variables and online cases.
A code must be assigned to exclude from the analysis those who did not respond and differentiate them from those who did.
There are three analyses that correspond to three different objectives:
- Univariate analyses: analyses that are performed on a single variable or characteristic.
- bivariate analyses: linking two variables, we want to cross data to analyze variations more subtly such as the interest of politics according to city or age.
- multivariate analyses: we think that an explained phenomenon is never explained by a single independent variable; on the other hand, we want to introduce controls in order to control relations through the purification technique.
A distinction must be made between a descriptive analysis that attempts to describe a "factual state" that is made univariate or bivariate.
Types of univariate analyses[modifier | modifier le wikicode]
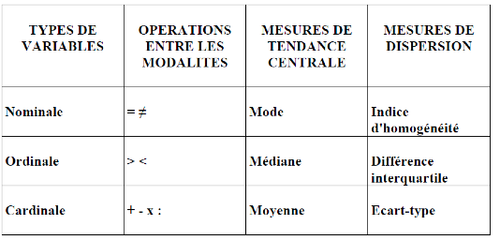
Types of variables and operations between methods[modifier | modifier le wikicode]
There are different types of univariate analyses, these techniques depend on the type of variable:
- nominal variables: only equivalence or difference operations can be performed.
- ordinal variables: allows to order i. e. to categorize according to an order from the smallest to the largest.
Note: Ordinal and cardinal variables are categorical, discrete data, distances cannot be seen.
- cardinal variables: allow the four basic arithmetic operations to be performed in addition to the previous operations.
Central trend measurement[modifier | modifier le wikicode]
When carrying out a quantitative analysis, it is necessary to consider the type of variables and then choose the tool to use. We can distinguish between two main types of measures, i.e. between two types of information that we want to have single variables:
- central trend measures ;
- dispersion measurements.
Note: Depending on the variable, the measurements are different.
The mean is a measure of a central trend value that can be applied to the cardinal variables, but it cannot be applied to the categorical variables. The median is the category that separates the statistical series in two with the same number of cases on either side.
This is important information that forms the starting point for this type of data description, allowing us to know what to do next in the case of more sophisticated analyses.
Measurement of dispersions[modifier | modifier le wikicode]
Dispersion measurements are also distinguished: the basic measure is the standard deviation, which is a standardized measure that varies from -1 to +1 of the variance, which is the measure that indicates how individuals are distributed.
Variance is very important for calculating the probability of error. Different measures are required depending on the unit of measurement of the variable, and account must be taken of the central trend and dispersion measure as the standard deviation that is the key coefficient throughout the quantitative analysis.
Types of bivariate analyses[modifier | modifier le wikicode]
In this context we wish to cross characteristics either in a descriptive or an explanatory perspective. Depending on the type of variable, different techniques are used to analyze and process the data.
Both dependent and independent variables need to be addressed. When cross-checking, we must look at the dependent and independent variable if we are dealing with categorical or ordinal variables that make it possible to distinguish three main families of types of analysis:
- categorical / nominal - nominal variables: contingency tables are made, other techniques cannot be used. Most of the time in political science we are dealing with this type of variables, because the answers give rise to ordinal variables. There are coefficients that make it possible to give a single measure of the relationship between these two variables, such as Cramer's V, which makes it possible to see the association between categorical variables. To interpret, it is important that the total percentage should always refer to the categories of the independent variable; we want to see how the distribution on the dependent variable depends on the functions in the independent variable. The number of cases indicates whether the process is statistically representative, as the sample size affects the measurement.
- cardinal-cardinal variables: we no longer cross tabulate, we have other tools and in particular the regression and correlation tool:
- covariation: when we have two continuous variables, when one increases the other increases proportionally or inversely proportional, the two variables are linked in this direction.
- correlation: it is simply a standardised covariation that is between -1 and +1. Standardisation is used to compare variables that are measured in a different way; if, for example, we have scales from 0 to 10 and scales from 0 to 5, we cannot compare these variables, so we must make sure that this information is standardised. Variables can be repeated on the same scale or software that calculates a standardized correlation.
- regression: in a correlation one is in a descriptive perspective, one does not seek to see a direction of causality in a regression one wants to see if two variables are associated, related, correlated.
- Nominal independent variables - cardinal dependent variables: cross tabulations, correlations and regressions cannot be applied; an analysis of variance or covariance is carried out, the simplest case of which is a comparison of averages, which could for example be the number of times that individuals participate in an election according to the canton.
Linear regression[modifier | modifier le wikicode]
It is a very varied and sometimes complex set of tools, but it is the main tool. Linear regression is the main element; much of the quantitative analysis done in social science relies on linear regression.
We talk about linearity, because we postulate that there is a linear relationship between the variables we are studying, in other words there is a linear function behind this relationship; however, we can also envisage regressions that are not only linear.
It is assumed that what we want to explain is a linear function of one or more independent variables. This is crucial, as linear regression is only a subset of a larger family of regression analyses that is not based on a linearity idea between the two variables.
The simplest model is with an explanatory variable such as, for example, political participation based on political interest.
In descriptive terms, there is a strong correlation between these two variables; if a hypothesis says that it is the interest in politics that influences participation, then a regression analysis is done.
There is always the problem of endogeneity in this type of analysis, we postulate that the interest in politics determines participation; we could also postulate that the more we participate, the more we develop an interest in politics.
Political participation is a linear function of the interest in politics "plus" a constant factor: the value of Y when X is equal to 0, i. e. what is my level of participation when the interest in politics is nil. At the bottom it is where the regression line crosses the ordinate axis.
In multivariate analysis, there is always a margin of error; one thing is related if you have survey data related to the margin of error between population and sample, but regardless of whether you are working on samples or an overall population; There is a term of error that comes into play, because there is always something that influences what we want to explain and which is not included in the regression model, such as education, age, social, institutional and other factors.
In fact, the E groups together the unexplained variance, i. e. everything that could explain Y, but is not introduced into the model, it is the problem of the model's under-specification, i. e. the model specification issue; the more variables a model has more variables, the more likely it is to be underspecified and the less variation in the Y and the higher the E in terms of error, the less likely it is to be underspecified.
This suggests that not including some variables in an explanatory model with two major consequences:
- the model is under-specified, there is little explanation of the variability of Y with this model, i. e. the factors strongly correlated with what we want to study.
- the second reason is related to the control of variables, because if one introduces interest in politics, a third variable can influence interest in politics and participation in politics; the association is misleading.
We want to include the maximum number of variables that we think can directly influence Y or indirectly making the relationship between X and Y false or only apparent.
The B is the regression coefficient, i. e. the slope of the regression line giving the strength of the effect of the X because it is multiplied by X, i. e. the higher the effect of X, the higher the B is.
B can be non-standardized or standardized." Standardization "means standardizing and the goal is to be able to compare different coefficients.
One is in an additive logic, there are "+"; one assumes that the variation of Y is a linear function is additive or cumulative of the effect of all the other variables introduced in the model.
Regression line[modifier | modifier le wikicode]
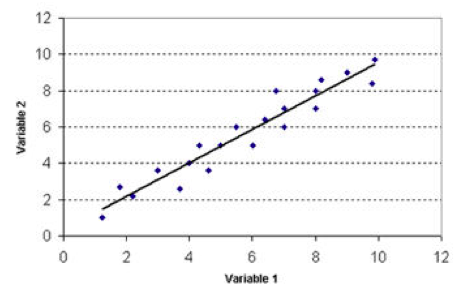
The regression line represents the linear regression function. We want to see how much more Y increases when we increase X. Let us admit that (0;12) is the interest in politics and the other one political participation; we can see that there is a fairly strong correlation between the two; when we have an increase in political interest, we increase political participation.
The blue dots represent the cases, the regression line is the estimation of the values and so we will look at the extent to which and how this line encounters a cloud of dots.
The quality of the model has to do with the quality of the estimate, which depends very much on how the points are distributed. It is possible that the point cloud may be estimated for a straight line that has the same slope, however the quality of this effect is the same while it is different because the straight line makes only a much more accurate approximation of the point cloud where the points are close to the right.
It should be kept in mind that one of the main instruments used for quantitative analysis when using interval or cardinal variables and correlation or regression analysis.
The idea of linear regression which is a subset of a larger set is based on the idea of a linear function between X and Y; we try to estimate a cloud of points which represents the crossing between the two variables in the sample, so we will analyze the regression line and its slope. If the slope is 0 then Y doesn't change when you change X, you may be very interested in politics, but you always participate at the same level.
Multivariate analyses[modifier | modifier le wikicode]
Regression analysis[modifier | modifier le wikicode]
Depending on the type of variables that you want to explain, you can or cannot apply the linear regression tool, for example, there is logistic regression in the case of dummies, either absence or presence, you cannot apply linear regression, because the basic assumptions are not guaranteed.
Ppath analysis[modifier | modifier le wikicode]
One of the problems with regression analysis is that Y is assumed to be a linear function of the sum of all independent variables, and as a result, we only look at the direct effects of model variables; however, what happens when we want to look at indirect effects?
We're doing a causal pathway analysis; There are regression coefficients that may or may not be significant, but we can see causal pathways, i. e. we can see how the left values influence participation not directly, but indirectly to know that being left-wing makes it more likely to be integrated in certain types of network develop an internet for a certain issue that allows to develop a feeling of individual efficiency and a higher intensity of participation. Intermediate variables are introduced.
Instead of having an indication, we have several because each variable can or is a dependent variable, we make a sum of equations.
Factor analysis[modifier | modifier le wikicode]
The objective of this analysis is to reduce the complexity that one can have when one has a data matrix with many variables and cases and wants to have a more succinct index.
When we talked about the operationalization of complex concepts, we arrived at a final stage of construction; factor analysis allows us to construct indexes by analyzing the underlying links that explain the variation on a multiple set of indicators.
It is a tool frequently used in political science, especially when studying changes in values.
Multi-level analysis[modifier | modifier le wikicode]
Previously all measures were concerned with individual variables, now there are context properties that are not of the individual that can influence political participation such as the electoral system or the type of political system.
From a normal regression point of view there are ways to short-circuit the problem, one cannot integrate contextual factors in the analysis one can simply compare.
Multi-level analysis makes it possible to perform a multi-level regression analysis, adding context properties and not just individual properties; integrating individual and contextual properties. There is this important development in political science.
Type of qualitative methods[modifier | modifier le wikicode]
A distinction can be made between content analysis and discourse analysis. There is no consensus in the literature on these terms, some believe that discourse analysis is a type of content analysis and others do not.
Content analysis[modifier | modifier le wikicode]
Content analysis is about weight, it's more descriptive, it's about the different issues raised by people. A later distinction can be made:
- thematic: we count the number of times such a theme appears in a speech.
- lexical: analysis based on the analysis of occurrences or co-occurrences, i. e. a qualitative analysis that has elements of quantitative analysis.
Discourse Analysis[modifier | modifier le wikicode]
It is an interpretative analysis, we are talking about a family of techniques, we can say that we are interested in how and the effects of a given discourse.
To simplify, content analysis is rather descriptive and explanatory discourse analysis.
Steps of the thematic analysis[modifier | modifier le wikicode]
There are five main stages:
- Familiarization (pre-analysis): Familiarity with the available equipment is essential.
- identification of a thematic framework (coding scheme, index): way of coding information or identifying the thematic framework.
- indexing (coding): reducing information.
- cartography (categorization and reduction of data): creation of typologies, classifications, reduction of data in order to be able to interpret them.
- mapping and interpretation (analysis and interpretation)
Stages of discourse analysis[modifier | modifier le wikicode]
- Pre-analysis
- Identification of relevant elements
- Systematic analysis based on identified elements