Trattamento dei dati
| Faculté | Faculté des sciences de la société |
|---|---|
| Département | Département de science politique et relations internationales |
| Professeur(s) | Marco Giugni[1] |
| Cours | Introduzione ai metodi della scienza politica |
Lectures
L'analisi dei dati quantitativi è molto diversa dall'analisi dei dati qualitativi; si tratta di due pratiche di ricerca molto diverse, se non opposte.
Ci concentreremo sull'analisi quantitativa, che in realtà è più facile dell'analisi qualitativa dei dati, se non altro perché ci sono routine istituzionalizzate.
Matrice di dati[modifier | modifier le wikicode]
Si tratta di una matrice che incrocia i casi studiati con un certo numero di variabili, vale a dire le variabili di colonna e i casi di riga.
Si dovrebbe assegnare un codice per escludere dall'analisi coloro che non hanno risposto e per differenziarli da coloro che hanno risposto.
Ci sono tre analisi che corrispondono a tre diversi obiettivi:
- analisi univariate: analisi che vengono effettuate su una singola variabile o caratteristica.
- analisi bivariata: collegando due variabili, vogliamo incrociare i dati per analizzare variazioni più sottili come l'interesse della politica a seconda della città o dell'età.
- analisi multivariate: pensiamo che un fenomeno spiegato non sia mai spiegato da una singola variabile indipendente; d'altra parte vogliamo introdurre controlli per controllare le relazioni attraverso la tecnica di purificazione. Tradotto con www.DeepL.com/Translator
Si deve distinguere tra un'analisi descrittiva che cerca di descrivere una "situazione di fatto" che è univariata o bivariata.
Tipi di analisi univariata[modifier | modifier le wikicode]
Types de variables et opérations entre modalités[modifier | modifier le wikicode]
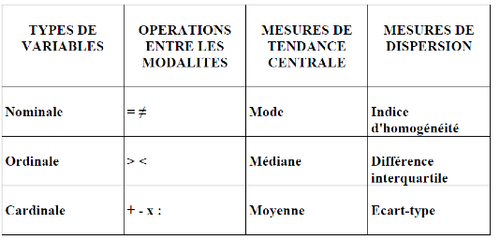
Esistono diversi tipi di analisi univariate, queste tecniche dipendono dal tipo di variabile:
- variabili nominali: possono essere eseguite solo operazioni di equivalenza o di differenza.
- variabili ordinali: permette di ordinare, cioè di classificare secondo un ordine dal più piccolo al più grande.
Nota: le variabili ordinali e cardinali sono categoriche, si basano su dati discreti, le distanze non sono visibili.
- variabili cardinali: oltre alle operazioni precedenti, consentono di eseguire le quattro operazioni aritmetiche di base.
Misurazione di tendenza centrale[modifier | modifier le wikicode]
Quando si esegue un'analisi quantitativa, è necessario considerare il tipo di variabili e poi scegliere lo strumento da utilizzare. Possiamo distinguere tra due tipi principali di misure, cioè tra due tipi di informazioni che vogliamo avere variabili uniche:
- misure di tendenza centrale
- misure di dispersione.
Nota: a seconda della variabile, le misure sono diverse.
La media è una misura centrale del valore di tendenza che può essere applicata a variabili cardinali, ma non può essere applicata a variabili categoriche. La mediana è la categoria che separa le serie statistiche in due con lo stesso numero di casi da un lato e dall'altro.
Si tratta di informazioni importanti che costituiscono il punto di partenza per questo tipo di descrizione dei dati per determinare cosa fare successivamente nel caso di analisi più sofisticate.
Mesure de dispersions[modifier | modifier le wikicode]
On distingue aussi des mesures de dispersions : la mesure de base est l’écart-type qui est une mesure standardisée qui varie de -1 à +1 de la variance qui est la mesure qui indique de quelle manière sont distribués les individus.
La variance est très importante pour calculer la probabilité d’erreur. Il faut différentes mesures selon l’unité de mesure de la variable et il faut tenir compte de la mesure de tendance centrale et de dispersion comme l’écart-type qui est le coefficient clef dans toute l’analyse quantitative.
Tipi di analisi bivariata[modifier | modifier le wikicode]
In questo contesto, vogliamo incrociare le caratteristiche in una prospettiva descrittiva o esplicativa. A seconda del tipo di variabile, esistono diverse tecniche di analisi ed elaborazione dei dati.
Devono essere considerate sia le variabili dipendenti che quelle indipendenti. All'incrocio, dobbiamo guardare la variabile dipendente e indipendente per vedere se si tratta di variabili categoriche o ordinali che permettono di distinguere tre principali famiglie di tipi di analisi:
- variabili categorica / nominale - nominali: vengono elaborate tabelle di contingenza, non è possibile utilizzare altre tecniche. La maggior parte delle volte nelle scienze politiche ci troviamo di fronte a questo tipo di variabili, perché le risposte danno origine a variabili ordinali. Ci sono coefficienti che ci permettono di dare una misura unica della relazione tra queste due variabili, come il V di Cramer, che ci permette di vedere l'associazione tra variabili categoriche. Per interpretare, è importante che la percentuale totale deve sempre riferirsi alle categorie della variabile indipendente; vogliamo vedere come la distribuzione della variabile dipendente dipende dalle funzioni della variabile indipendente. L'indicazione del numero di casi mostra se il processo è statisticamente rappresentativo, in quanto la dimensione del campione influenza la misurazione.
- variabili cardinali - cardinali: non facciamo più una crosstabulazione, ma utilizziamo altri strumenti e in particolare lo strumento di regressione e correlazione:
- covariata: quando ci sono due variabili continue, quando una aumenta l'altra aumenta proporzionalmente o inversamente proporzionale, le due variabili sono collegate in questa direzione.
- correlazione: si tratta semplicemente di una covariata standardizzata, cioè tra -1 e +1. Ci standardizziamo per assicurare che le variabili che sono misurate diversamente alla base siano confrontate; se, per esempio, abbiamo scale da 0 a 10 e scale da 0 a 5 non possiamo confrontare queste variabili allora dobbiamo fare in modo che queste informazioni siano standardizzate. Le variabili possono essere ripetute sulla stessa scala o su un software che calcola una correlazione standardizzata.
- regressione: in una correlazione siamo in una prospettiva descrittiva, non cerchiamo di vedere una direzione di causalità in una regressione che vogliamo vedere se due variabili sono associate, collegate, correlate.
- variabili indipendenti nominali - variabili cardinali dipendenti: non possono essere applicate le tabulazioni incrociate, le correlazioni e le regressioni; viene effettuata un'analisi della varianza o della covarianza, il cui caso più semplice è il confronto delle medie, che potrebbe ad esempio essere il numero di volte che gli individui partecipano a un'elezione secondo il cantone.
Regressione lineare[modifier | modifier le wikicode]
Si tratta di un insieme di strumenti molto vario e a volte complesso, ma è lo strumento principale. La regressione lineare è l'elemento principale; gran parte dell'analisi quantitativa nelle scienze sociali si basa sulla regressione lineare.
Parliamo di linearità, perché assumiamo che ci sia una relazione lineare tra le variabili che studiamo, in altre parole, c'è una funzione lineare dietro questa relazione; tuttavia, possiamo anche considerare regressioni che non sono solo lineari.
Si presume che ciò che si vuole spiegare è una funzione lineare di una o più variabili indipendenti. Questo è fondamentale, perché la regressione lineare è solo un sottoinsieme di una famiglia più ampia di analisi di regressione che non si basa su un'idea di linearità tra le due variabili.
Il modello più semplice è quello con una variabile esplicativa come, ad esempio, la partecipazione politica a seconda dell'interesse politico.
In termini descrittivi c'è una forte correlazione tra queste due variabili; se un'ipotesi dice che è l'interesse politico che influenza la partecipazione, allora si effettua un'analisi di regressione.
Abbiamo sempre il problema dell'endogeneità in questo tipo di analisi, ipotizziamo che l'interesse per la politica determina la partecipazione; potremmo anche ipotizzare che più partecipiamo, più sviluppiamo un interesse per la politica.
La partecipazione politica è una funzione lineare di interesse politico "più" un fattore costante, cioè il valore di Y quando X è uguale a 0, cioè qual è il mio livello di partecipazione quando l'interesse politico è zero. In fondo è dove la linea di regressione attraversa l'asse y.
Nell'analisi multivariata, c'è sempre un margine di errore; una cosa è correlata se abbiamo dati di indagine relativi al margine di errore tra popolazione e campione, ma indipendentemente dal fatto che stiamo lavorando su campioni o su una popolazione complessiva; c'è sempre un termine di errore coinvolto, perché c'è sempre qualcosa che influenza ciò che vogliamo spiegare e che non è incluso nel modello di regressione come, ad esempio, l'istruzione, l'età, il contesto sociale, istituzionale, ecc.
Infatti, la E raggruppa la varianza inspiegabile, cioè tutto ciò che potrebbe spiegare Y, ma non viene introdotto nel modello, è il problema della sottospecificazione del modello, cioè la questione relativa alla specificazione del modello; più variabili ha un modello, più è probabile che sia sottospecificato e meno variazioni nella Y sono spiegate e più alta è la E in termini di errore, la E è ridotta al minimo.
Ciò suggerisce che non includere alcune variabili in un modello esplicativo con due conseguenze principali:
- il modello è sottospecificato, c'è poca spiegazione della variabilità di Y con questo modello, cioè i fattori fortemente correlati con ciò che vogliamo studiare.
- la seconda ragione è legata al controllo delle variabili, perché se si introduce l'interesse per la politica, una terza variabile può influenzare l'interesse per la politica e la partecipazione alla politica; l'associazione è fuorviante.
Vogliamo includere quante più variabili possibili che pensiamo possano influenzare direttamente Y o indirettamente rendendo la relazione tra X e Y falsa o solo apparente.
Il B è il coefficiente di regressione, cioè la pendenza della linea di regressione che dà la forza dell'effetto X perché è moltiplicato per X, cioè più forte è l'effetto X, più alto è il B.
Il B può essere non standardizzato o standardizzato. "Standardizzazione" significa normalizzazione e lo scopo è quello di poter confrontare diversi coefficienti.
Siamo in una logica additiva, ci sono "+"; supponiamo che la variazione di Y sia una funzione lineare sia additiva o cumulativa dell'effetto di tutte le altre variabili introdotte nel modello.
Linea di regressione[modifier | modifier le wikicode]
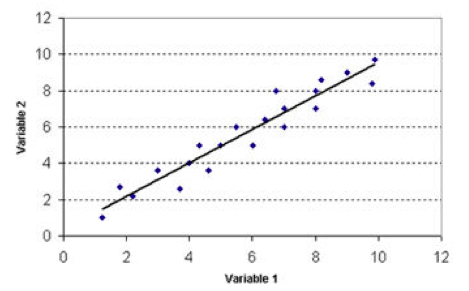
La linea di regressione rappresenta la funzione di regressione lineare. Vogliamo guardare a quanto aumenta Y quando aumentiamo X. Supponiamo che gli (0; 12) siano l'interesse per la politica e l'altra partecipazione politica; possiamo vedere che c'è una correlazione abbastanza forte tra i due, quando abbiamo un aumento dell'interesse per la politica aumentiamo la partecipazione politica.
I punti blu rappresentano i casi, la linea di regressione è la stima dei valori e quindi esamineremo quanto e come questa linea incontra una nuvola di punti.
La qualità del modello ha a che fare con la qualità della stima, che dipende molto da come vengono distribuiti i punti. E' possibile che la nuvola di punti sia stimata per una linea che ha la stessa pendenza, ma la qualità di questo effetto è la stessa mentre è diversa perché la linea fa solo un'approssimazione molto più accurata della nuvola di punti o i punti sono vicini alla linea.
Va notato che uno dei principali strumenti preferiti per l'analisi quantitativa quando si tratta di variabili d'intervallo o cardinali e di analisi di correlazione o regressione.
L'idea di regressione lineare, che è un sottoinsieme di un insieme più ampio, si basa sull'idea di una funzione lineare tra X e Y; cerchiamo di stimare una nuvola di punti che rappresenta l'intersezione tra le due variabili del campione, quindi analizzeremo la linea di regressione e la sua pendenza. Se la pendenza è 0 allora Y non cambia quando si cambia X, si può essere molto interessati alla politica, ma si partecipa sempre allo stesso livello.
Analisi multivariate[modifier | modifier le wikicode]
Analisi di regressione[modifier | modifier le wikicode]
A seconda del tipo di variabili che si desidera spiegare, è possibile o meno applicare lo strumento di regressione lineare, ad esempio, c'è regressione logistica nel caso di variabili fittizie o assenza o presenza, non è possibile applicare la regressione lineare, perché i presupposti di base non sono garantiti.
Analisi dei cammini causali (path analysis)[modifier | modifier le wikicode]
Uno dei problemi dell'analisi di regressione è che assumiamo che Y è una funzione lineare della somma di tutte le variabili indipendenti o quando guardiamo gli effetti diretti delle variabili in un modello; tuttavia, cosa succede quando vogliamo guardare agli effetti indiretti?
Facciamo un'analisi dei "percorsi causali"; ci sono coefficienti di regressione che possono essere o meno significativi, ma possiamo vedere i percorsi causali, cioè possiamo vedere come i valori della sinistra influenzano la partecipazione non direttamente, ma indirettamente, cioè che essendo sulla sinistra rende più probabile che saremo integrati in certi tipi di reti si sviluppa una Internet per un certo problema che ci permette di sviluppare un sentimento di efficacia individuale che ci fa avere una maggiore intensità di partecipazione. Vengono introdotte variabili intermedie.
Invece di avere un'indicazione, ne abbiamo diverse perché ogni variabile può o è una variabile dipendente, facciamo una somma di equazioni.
Analisi fattoriale[modifier | modifier le wikicode]
Si tratta di un'analisi che mira a ridurre la complessità che si può ottenere quando si dispone di una data matrix con molte variabili e casi e si desidera un indice più succinto.
Quando abbiamo parlato di rendere operativi concetti complessi, abbiamo raggiunto l'ultima fase di costruzione; l'analisi dei fattori ci permette di costruire indici analizzando i collegamenti sottostanti che spiegano la variazione su un insieme multiplo di indicatori.
E' uno strumento frequentemente utilizzato nelle scienze politiche e in particolare nello studio dei cambiamenti di valori.
Analisi multilivello[modifier | modifier le wikicode]
In precedenza tutte le misure riguardavano variabili individuali, ora ci sono proprietà di contesto che non sono dell'individuo che possono influenzare la partecipazione politica come il sistema elettorale o il tipo di sistema politico.
In una normale prospettiva di regressione ci sono modi per aggirare il problema, non si possono integrare fattori contestuali nell'analisi che si possono semplicemente confrontare.
L'analisi multilivello consente di effettuare analisi di regressione multilivello, aggiungendo proprietà contestuali e non solo proprietà individuali, integrando proprietà individuali e contestuali. C'è questo importante sviluppo delle scienze politiche.
Tipo di metodi qualitativi[modifier | modifier le wikicode]
Si può fare una distinzione tra analisi dei contenuti e analisi del discorso. Non c'è consenso in letteratura su questi termini, alcuni ritengono che l'analisi del discorso sia un tipo di analisi dei contenuti e altri no.
Analisi del contenuto[modifier | modifier le wikicode]
L'analisi dei contenuti è interessata al peso, è più descrittiva, è interessata alle diverse questioni sollevate dalle persone. Un'ulteriore distinzione può essere fatta:
- tematico: contiamo il numero di volte che un tema di questo tipo appare in un discorso.
- lessicale: analisi basata sull'analisi di eventi o co-occorrenze, cioè un'analisi qualitativa che contiene elementi di analisi quantitativa.
Analisi del parlato[modifier | modifier le wikicode]
È un'analisi interpretativa, stiamo parlando di una famiglia di tecniche, possiamo dire che siamo interessati a come e quali sono gli effetti di un dato discorso.
Per semplificare, l'analisi dei contenuti è un'analisi del discorso descrittiva e esplicativa.
Fasi dell'analisi tematica[modifier | modifier le wikicode]
Ci sono cinque fasi principali:
- familiarizzazione (pre-analisi): prima di tutto, è necessario familiarizzare con le attrezzature disponibili.
- identificazione di un quadro tematico (schema di codifica, indice): come codificare le informazioni o identificare il quadro tematico.
- indicizzazione (codifica): ridurre le informazioni.
- mappatura (categorizzazione e riduzione dei dati): creazione di tipologie, classificazioni, riduzione dei dati per poterli interpretare.
- mappatura e interpretazione (analisi e interpretazione)
Fasi dell'analisi del parlato[modifier | modifier le wikicode]
- Pre-analisi
- Identificazione degli elementi rilevanti
- Analisi sistematica basata sugli elementi identificati