Procesamiento de datos
| Faculté | Faculté des sciences de la société |
|---|---|
| Département | Département de science politique et relations internationales |
| Professeur(s) | Marco Giugni[1] |
| Cours | Introducción a los métodos de la ciencia política |
Lectures
El análisis de los datos cuantitativos es muy diferente del análisis de los datos cualitativos; son dos prácticas de investigación muy diferentes, si no opuestas.
Nos centraremos en el análisis cuantitativo, que en realidad es más fácil que el análisis cualitativo de datos, aunque sólo sea porque hay rutinas institucionalizadas.
Matriz de datos[modifier | modifier le wikicode]
Es una matriz que cruza los casos estudiados con una serie de variables, a saber, variables de columna y casos de fila.
Se debe asignar un código para excluir del análisis a los que no respondieron y para diferenciarlos de los que sí respondieron.
Hay tres análisis que corresponden a tres objetivos diferentes:
- análisis univariados: análisis que se realizan sobre una sola variable o característica.
- análisis bivariables: vinculando dos variables, queremos cruzar datos para analizar variaciones más sutiles como el interés de la política según la ciudad o la edad.
- análisis multivariados: pensamos que un fenómeno explicado nunca se explica por una sola variable independiente; por otro lado queremos introducir controles para controlar las relaciones a través de la técnica de purificación.
Hay que distinguir entre un análisis descriptivo que pretende describir una "situación de hecho" univariada o bivariada.
Tipos de análisis univariados[modifier | modifier le wikicode]
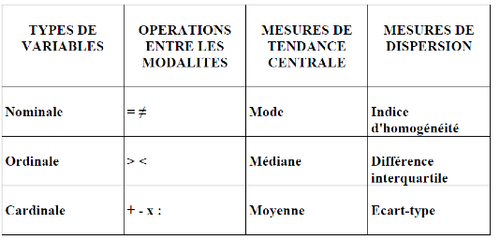
Tipos de variables y operaciones entre modalidades[modifier | modifier le wikicode]
Existen diferentes tipos de análisis univariados, estas técnicas dependen del tipo de variable:
- variables nominales: sólo se pueden realizar operaciones de equivalencia o diferencia.
- variables ordinales: permite ordenar, es decir, categorizar según un orden desde el más pequeño hasta el más grande.
Nota: las variables ordinales y cardinales son categóricas, se basan en datos discretos, las distancias no se pueden ver.
- variables cardinales: además de las operaciones anteriores, permiten realizar las cuatro operaciones aritméticas básicas.
Medición central de tendencias[modifier | modifier le wikicode]
Al realizar un análisis cuantitativo, es necesario considerar el tipo de variables y luego elegir la herramienta a utilizar. Podemos distinguir entre dos tipos principales de medidas, es decir, entre dos tipos de información que queremos que tengan variables únicas:
- medidas de tendencia central
- medidas de dispersión.
Nota: dependiendo de la variable, las medidas son diferentes.
La media es una medida de valor de tendencia central que puede aplicarse a variables cardinales, pero no a variables categóricas. La mediana es la categoría que separa las series estadísticas en dos con el mismo número de casos por un lado y por el otro.
Esta es una información importante que constituye el punto de partida para este tipo de descripción de datos para determinar qué hacer a continuación en el caso de análisis más sofisticados.
Medición de dispersión[modifier | modifier le wikicode]
También se distinguen las medidas de dispersión: la medida básica es la desviación estándar, que es una medida estandarizada que varía de -1 a +1 de la varianza, que es la medida que indica cómo se distribuyen los individuos.
La varianza es muy importante para calcular la probabilidad de error. Se requieren diferentes medidas dependiendo de la unidad de medida de la variable y la medida de la tendencia central y la dispersión, como la desviación estándar, que es el coeficiente clave, debe tenerse en cuenta a lo largo del análisis cuantitativo.
Tipos de análisis bivariados[modifier | modifier le wikicode]
En este contexto, deseamos cruzar características en una perspectiva descriptiva o explicativa. Dependiendo del tipo de variable, existen diferentes técnicas para analizar y procesar los datos.
Se deben considerar tanto las variables dependientes como las independientes. Al cruzar, debemos mirar la variable dependiente e independiente para ver si se trata de variables categóricas u ordinales que permiten distinguir tres familias principales de tipos de análisis:
- variables categóricas / nominales - nominales: se realizan tablas de contingencia, no se pueden utilizar otras técnicas. La mayor parte del tiempo en la ciencia política se trata de este tipo de variables, porque las respuestas dan lugar a variables ordinales. Existen coeficientes que nos permiten dar una medida única de la relación entre estas dos variables, como la V de Cramer, que nos permite ver la asociación entre variables categóricas. Para interpretar, es importante que el porcentaje total se refiera siempre a las categorías de la variable independiente; queremos ver cómo la distribución de la variable dependiente depende de las funciones de la variable independiente. La indicación del número de casos muestra si el proceso es estadísticamente representativo, ya que el tamaño de la muestra afecta a la medición.
- variables cardinales - cardinales: ya no hacemos una tabulación cruzada, utilizamos otras herramientas y en particular la herramienta de regresión y correlación:
- covariable: cuando hay dos variables continuas, cuando una aumenta la otra aumenta proporcional o inversamente proporcional, las dos variables están vinculadas en esta dirección.
- correlación: es simplemente un covariable estandarizado, es decir, está entre -1 y +1. Estandarizamos para asegurar que se comparen las variables que se miden de manera diferente en la base; si, por ejemplo, tenemos escalas de 0 a 10 y escalas de 0 a 5, no podemos comparar estas variables, entonces debemos asegurarnos de que esta información esté estandarizada. Las variables pueden repetirse en la misma escala o software que calcula una correlación estandarizada.
- regresión: en una correlación estamos en una perspectiva descriptiva, no intentamos ver una dirección de causalidad en una regresión queremos ver si dos variables están asociadas, vinculadas, correlacionadas.
- variables independientes nominales - variables dependientes cardinales: no se pueden aplicar tabulaciones cruzadas, correlaciones y regresiones; se realiza un análisis de varianza o covarianza, cuyo caso más simple es una comparación de promedios, que podría ser, por ejemplo, el número de veces que los individuos participan en una elección según el cantón.
Regresión lineal[modifier | modifier le wikicode]
Es un conjunto de herramientas muy variado y a veces complejo, pero es la herramienta principal. La regresión lineal es el elemento principal; gran parte del análisis cuantitativo en las ciencias sociales se basa en la regresión lineal.
Hablamos de linealidad, porque suponemos que hay una relación lineal entre las variables que estudiamos, es decir, que hay una función lineal detrás de esta relación; sin embargo, también podemos considerar regresiones que no son sólo lineales.
Se asume que lo que queremos explicar es una función lineal de una o más variables independientes. Esto es crucial, porque la regresión lineal es sólo un subconjunto de una familia más amplia de análisis de regresión que no se basa en una idea de linealidad entre las dos variables.
El modelo más sencillo es con una variable explicativa como, por ejemplo, la participación política según el interés político.
En términos descriptivos existe una fuerte correlación entre estas dos variables; si una hipótesis dice que es el interés político lo que influye en la participación, entonces se hace un análisis de regresión.
Siempre tenemos el problema de la endogeneidad en este tipo de análisis, postulamos que el interés por la política determina la participación; también podríamos postular que cuanto más participamos, más desarrollamos un interés por la política.
La participación política es una función lineal de interés político "más" un factor constante, es decir, el valor de Y cuando X es igual a 0, es decir, cuál es mi nivel de participación cuando el interés político es cero. En la parte inferior es donde la línea de regresión cruza el eje y.
En el análisis multivariado siempre hay un margen de error; una cosa está relacionada si tenemos datos de encuestas relacionados con el margen de error entre población y muestra, pero independientemente de si estamos trabajando con muestras o con una población en general; siempre hay un término de error involucrado, porque siempre hay algo que influye en lo que queremos explicar y que no está incluido en el modelo de regresión como, por ejemplo, la educación, la edad, el contexto social, institucional, etc.
De hecho, la E agrupa la varianza no explicada, es decir, todo lo que podría explicar la Y, pero no se introduce en el modelo, es el problema de la subespecificación del modelo, es decir, la cuestión relativa a la especificación del modelo; cuantas más variables tenga un modelo, más probable es que se subespecifique y se expliquen menos variaciones en la Y, y cuanto más alta sea la E en términos de error, más se reducirá a un mínimo la E.
Esto sugiere que no incluir algunas variables en un modelo explicativo tiene dos consecuencias principales:
- el modelo está subespecificado, hay poca explicación de la variabilidad de Y con este modelo, es decir, los factores fuertemente correlacionados con lo que queremos estudiar.
- la segunda razón está relacionada con el control de las variables, porque si se introduce el interés en la política, una tercera variable puede influir en el interés en la política y la participación en la política; la asociación es engañosa.
Queremos incluir tantas variables como sea posible que pensamos pueden influir directamente en Y o indirectamente haciendo que la relación entre X e Y sea falsa o sólo aparente.
La B es el coeficiente de regresión, es decir, la pendiente de la línea de regresión que da la fuerza del efecto X porque se multiplica por X, es decir, cuanto más fuerte es el efecto X, más alta es la B.
La B puede ser no estandarizada o estandarizada. "Estandarización" significa normalizar y el propósito es poder comparar diferentes coeficientes.
Estamos en una lógica aditiva, hay "+"; suponemos que la variación de Y es una función lineal es aditiva o acumulativa del efecto de todas las demás variables introducidas en el modelo.
Línea de regresión[modifier | modifier le wikicode]
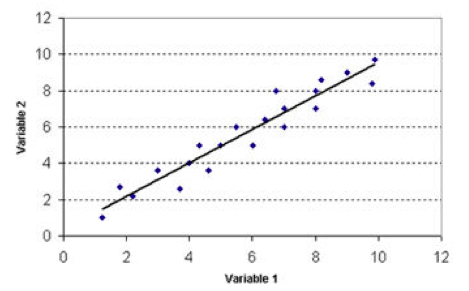
La línea de regresión representa la función de regresión lineal. Queremos ver cuánto aumenta Y cuando aumentamos X. Supongamos que los (0; 12) son el interés en la política y la otra participación política; podemos ver que hay una correlación bastante fuerte entre los dos, cuando tenemos un aumento en el interés en la política aumentamos la participación política.
Los puntos azules representan los casos, la línea de regresión es la estimación de los valores, por lo que veremos hasta dónde y cómo esta línea se encuentra con una nube de puntos.
La calidad del modelo tiene que ver con la calidad de la estimación, que depende mucho de cómo se distribuyen los puntos. Es posible que la nube de puntos se estime para una línea que tiene la misma pendiente, sin embargo la calidad de este efecto es la misma mientras que es diferente porque la línea sólo hace una aproximación mucho más precisa de la nube de puntos o los puntos están cerca de la línea.
Cabe señalar que es uno de los principales instrumentos preferidos para el análisis cuantitativo cuando se trata de variables de intervalo o cardinales y de análisis de correlación o regresión.
La idea de regresión lineal, que es un subconjunto de un conjunto mayor, se basa en la idea de una función lineal entre X e Y; tratamos de estimar una nube de puntos que represente la intersección entre las dos variables de la muestra, por lo que analizaremos la línea de regresión y su pendiente. Si la pendiente es 0 entonces Y no cambia cuando cambias X, puedes estar muy interesado en la política, pero siempre participas en el mismo nivel.
Análisis multivariados[modifier | modifier le wikicode]
Análisis de regresión[modifier | modifier le wikicode]
Dependiendo del tipo de variables que se quiera explicar, se puede o no aplicar la herramienta de regresión lineal, por ejemplo, hay regresión logística en el caso de variables ficticias, ya sea de ausencia o de presencia, no se puede aplicar regresión lineal, porque los supuestos básicos no están garantizados.
Análisis de las vías causales (path analysis)[modifier | modifier le wikicode]
Uno de los problemas del análisis de regresión es que asumimos que Y es una función lineal de la suma de todas las variables independientes o cuando observamos los efectos directos de las variables en un modelo; sin embargo, ¿qué sucede cuando queremos observar los efectos indirectos?
Hacemos un análisis de "caminos causales"; hay coeficientes de regresión que pueden o no ser significativos, pero podemos ver caminos causales, es decir, podemos ver cómo los valores de la izquierda influyen en la participación no directa, sino indirectamente, es decir, que el hecho de estar en la izquierda hace que sea más probable que nos integremos en ciertos tipos de redes desarrolla una Internet para un determinado tema que nos permite desarrollar un sentimiento de eficacia individual que nos hace tener una mayor intensidad de participación. Se introducen variables intermedias.
En lugar de tener una indicación, tenemos varias porque cada variable puede o es una variable dependiente, hacemos una suma de ecuaciones.
Análisis factorial[modifier | modifier le wikicode]
Es un análisis que busca reducir la complejidad que se puede lograr cuando se tiene una matriz de datos con muchas variables y casos y se desea un índice más sucinto.
Cuando hablamos de operacionalizar conceptos complejos, llegamos a la última etapa de construcción; el análisis factorial nos permite construir índices mediante el análisis de los vínculos subyacentes que explican la variación en un conjunto múltiple de indicadores.
Es una herramienta que se utiliza con frecuencia en la ciencia política y, en particular, en el estudio de los cambios de valores.
Análisis multinivel[modifier | modifier le wikicode]
Antes todas las medidas se referían a variables individuales, ahora hay propiedades de contexto que no son del individuo y que pueden influir en la participación política, como el sistema electoral o el tipo de sistema político.
En una perspectiva de regresión normal hay maneras de evitar el problema, no se pueden integrar factores contextuales en el análisis que simplemente se puede comparar.
El análisis multinivel permite el análisis de regresión multinivel, añadiendo propiedades de contexto y no sólo propiedades individuales; integrando propiedades individuales y contextuales. Existe este importante avance en la ciencia política.
Tipo de métodos cualitativos[modifier | modifier le wikicode]
Se puede hacer una distinción entre el análisis de contenido y el análisis del discurso. No hay consenso en la literatura sobre estos términos, algunos creen que el análisis del discurso es un tipo de análisis del contenido y otros no.
Análisis de contenido[modifier | modifier le wikicode]
El análisis de contenido se interesa por el peso, es más descriptivo, se interesa por las diferentes cuestiones planteadas por las personas. Se puede hacer otra distinción:
- temático: se cuenta el número de veces que un tema de este tipo aparece en un discurso.
- léxico: análisis basado en el análisis de ocurrencias o co-ocurrencias, es decir, un análisis cualitativo que tiene elementos de análisis cuantitativo.
Análisis de discurso[modifier | modifier le wikicode]
Es un análisis interpretativo, estamos hablando de una familia de técnicas, podemos decir que estamos interesados en cómo y cuáles son los efectos de un determinado discurso.
Para simplificar, el análisis de contenido es más bien descriptivo y explicativo.
Pasos en el análisis temático[modifier | modifier le wikicode]
Hay cinco pasos principales:
- familiarización (pre-análisis): en primer lugar, debe familiarizarse con el equipo disponible.
- identificación de un marco temático (esquema de codificación, índice): cómo codificar la información o identificar el marco temático.
- indexación (codificación): reduce la información.
- mapeo (categorización y reducción de datos): creación de tipologías, clasificaciones, reducción de datos para poder interpretarlos.
- mapping e interpretación (análisis e interpretación)
Pasos en el análisis de discurso[modifier | modifier le wikicode]
- Pre-análisis
- Identificación de elementos relevantes
- Análisis sistemático basado en los elementos identificados