Les coûts de production

Données clés
Professeur(s)	Milet, Emmanuel Sbergami, Federica^[1]^[2]^[3] Ferro-Luzzi , Giovanni
Cours	Introduction à la microéconomie

Lectures

Languages

Español

L'analyse des coûts de production est un aspect fondamental de l'organisation industrielle en microéconomie. Cette analyse est cruciale car l'objectif principal de tout agent économique, particulièrement les entreprises, est de maximiser ses bénéfices. L'étude des coûts de production aide à comprendre le comportement des entreprises dans différents contextes de marché, y compris la concurrence parfaite et diverses formes de concurrence imparfaite.

Les coûts de production sont des facteurs clés qui influencent les décisions de production et les prix. En d'autres termes, les stratégies et les programmes d'une entreprise dépendent fortement de ses choix en matière de facteurs de production. L'objectif ultime des entreprises est de maximiser leurs profits, et les coûts de production, qui affectent directement la fonction d'offre, jouent un rôle significatif dans la détermination des profits.

Cette analyse permet aux entreprises de prendre des décisions éclairées sur la quantité à produire, les technologies à utiliser, et les prix à pratiquer pour rester compétitives tout en maximisant leurs bénéfices. Les coûts peuvent inclure des éléments tels que les matières premières, le travail, l'énergie, et l'amortissement des équipements. En comprenant ces coûts et en les gérant efficacement, les entreprises peuvent optimiser leur production et renforcer leur position sur le marché.

L'analyse des coûts de production

La formule pour le profit des entreprises est en effet assez simple en théorie. Le profit (π) est calculé en soustrayant le coût total (CT) de la recette totale (RT). En formule mathématique, cela s'écrit :

π = RT − CT

Ici, π représente le profit, RT la recette totale, et CT le coût total.

La recette totale (RT) est calculée en multipliant le prix unitaire d'un bien ou d'un service par la quantité vendue. C'est-à-dire :

RT= Prix × Quantité vendue

Cette formule met en évidence l'importance du prix et du volume des ventes dans la génération de revenus pour une entreprise. Un prix élevé ou une grande quantité vendue peuvent tous deux augmenter la recette totale, tandis que la gestion efficace des coûts peut réduire le coût total, augmentant ainsi le profit. Cependant, il est important de noter que cette formule simplifiée ne prend pas en compte d'autres facteurs qui peuvent influencer le profit, tels que les coûts fixes et variables, les économies d'échelle, les conditions de marché, et la stratégie de prix. En pratique, la maximisation du profit est souvent plus complexe et nécessite une analyse détaillée de tous ces facteurs.

L'analyse des coûts de production occupe une place centrale dans la compréhension de la fonction d'offre de marché en microéconomie. Cette fonction d'offre est traditionnellement perçue comme une relation croissante entre le prix et la quantité offerte. Ce lien s'explique par le fait que, lorsque les prix augmentent, les entreprises sont incitées à produire davantage pour réaliser des profits plus élevés. Les coûts de production jouent un rôle crucial dans cette dynamique. Ils comprennent à la fois des coûts variables, qui changent avec le niveau de production, et des coûts fixes, qui restent constants indépendamment de la quantité produite. La compréhension de ces coûts permet aux entreprises de déterminer la quantité de production qui maximise leurs profits à différents niveaux de prix.

En parallèle, la théorie de la consommation examine les facteurs influençant la fonction de demande, qui indique la quantité d'un bien ou d'un service que les consommateurs sont prêts à acheter à différents prix. Cette demande est façonnée par des éléments tels que les revenus des consommateurs, leurs préférences, les prix des biens substituts et complémentaires, ainsi que leurs attentes futures. L'analyse de ces facteurs est essentielle pour comprendre comment les choix des consommateurs influencent la demande globale sur le marché.

Ainsi, l'analyse des coûts de production et la théorie de la consommation sont deux piliers de la microéconomie qui se complètent pour expliquer la dynamique du marché. D'une part, les entreprises évaluent leurs coûts de production pour définir leur offre, et d'autre part, les consommateurs prennent leurs décisions d'achat en fonction de divers facteurs influençant leur demande. La rencontre de l'offre et de la demande détermine l'équilibre du marché, influençant ainsi la formation des prix et la quantité de biens échangés. Cette compréhension intégrée de l'offre et de la demande est cruciale pour analyser l'économie de marché, les tendances de consommation et les stratégies d'entreprise.

Une entreprise simplifiée.

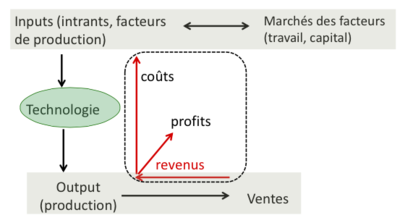
Ce graphique offre une représentation visuelle de la structure de base de la production et de l'économie d'une entreprise. Dans ce modèle, les intrants ou facteurs de production tels que le travail et le capital sont acquis sur les marchés correspondants et constituent la base de tout processus de production. Ces intrants sont ensuite transformés en produits ou services finis (outputs) grâce à la technologie, qui peut englober des méthodes de production, des équipements, et des connaissances spécialisées.

Une fois que la technologie a été utilisée pour transformer les intrants en outputs, ces derniers sont vendus sur le marché, générant ainsi des revenus pour l'entreprise. Ces revenus sont une fonction du prix auquel les biens ou services sont vendus et de la quantité de ces derniers qui est effectivement achetée par les consommateurs. Le diagramme suggère que les revenus et les coûts sont intrinsèquement liés, les coûts étant une conséquence nécessaire de la production. Ces coûts comprennent tout ce qui est requis pour produire l'output, y compris mais sans s'y limiter, les salaires, les coûts des matériaux, et l'amortissement du capital.

Les profits sont représentés de manière à illustrer leur nature dérivée, étant le résultat résiduel une fois que les coûts ont été soustraits des revenus. C'est le chiffre qui intéresse le plus les entreprises, car il mesure l'efficacité avec laquelle elles ont transformé leurs intrants en outputs rentables. Les profits sont essentiels non seulement pour la survie et la croissance de l'entreprise, mais aussi pour les décisions stratégiques concernant les investissements dans de nouvelles technologies ou l'expansion sur de nouveaux marchés.

Ce modèle schématique souligne également l'importance des marchés des facteurs de production, qui sont des éléments clés de l'environnement externe d'une entreprise. Ces marchés déterminent la disponibilité et le coût des intrants essentiels, influençant ainsi les coûts de production. Les entreprises doivent donc surveiller attentivement ces marchés pour optimiser leurs décisions en matière de coûts.

Toutefois, il est important de noter que ce schéma est une simplification du processus économique réel. Dans la réalité, les entreprises sont confrontées à des décisions beaucoup plus complexes, impliquant des facteurs externes variés tels que les changements de réglementation, les fluctuations de la demande du marché, et l'évolution rapide de la technologie. De plus, les entreprises doivent également gérer les coûts fixes et variables, les économies d'échelle, et les stratégies de prix différenciées pour rester compétitives. En résumé, bien que le schéma capture l'essence du processus économique des entreprises, il ne rend pas compte de l'ensemble des nuances et des complexités du monde des affaires réel.

Fonction de production et coûts totaux

Qu’est-ce que le coût de production ?

le coût d'opportunité

Le deuxième principe économique aborde un concept fondamental en microéconomie : le coût d'opportunité. Ce principe met en lumière que le coût réel de toute action, investissement ou acquisition n'est pas uniquement mesuré par le montant d'argent dépensé pour l'obtenir. Au-delà des transactions financières, le coût d'opportunité inclut également la valeur de la meilleure alternative à laquelle on a renoncé pour faire ce choix. Pour illustrer, considérons un individu qui décide de passer une heure à étudier au lieu de travailler où il pourrait gagner 20 euros. Le coût d'opportunité de cette heure d'étude n'est pas seulement l'effort ou l'énergie dépensée pour apprendre, mais aussi les 20 euros qu'il n'a pas gagnés en travaillant. Ainsi, le coût d'opportunité fournit une vision plus complète et précise des choix économiques.

En économie, ce concept est crucial car il souligne que chaque choix comporte un potentiel coût caché associé à la non-sélection d'une alternative. Les entreprises et les individus utilisent la notion de coût d'opportunité pour prendre des décisions informées et rationnelles, en comparant les bénéfices attendus d'une option par rapport à ceux de la meilleure alternative non choisie. La prise en compte du coût d'opportunité est donc essentielle pour comprendre les incitations et les comportements en économie. Elle pousse les décideurs à considérer non seulement les bénéfices immédiats mais aussi les bénéfices potentiels qui doivent être abandonnés. Cela permet de s'assurer que les ressources rares sont allouées de la manière la plus efficace possible pour maximiser la valeur et le bien-être.

Cout explicites vs implicites

Dans le contexte de la production d'un bien par une entreprise, les coûts sont souvent classés en deux catégories : explicites et implicites, reflétant les différents aspects des sacrifices économiques engagés dans le processus de production.

Les coûts explicites sont les paiements monétaires directs que l'entreprise doit débourser pour acquérir les facteurs de production nécessaires. Ces paiements peuvent inclure les salaires versés aux employés, les prix d'achat des matières premières, les loyers pour les installations ou l'équipement, les intérêts sur les emprunts, et toute autre dépense en espèces qui peut être enregistrée et comptabilisée. Ils sont souvent facilement quantifiables et sont enregistrés dans les livres comptables de l'entreprise, jouant un rôle clé dans le calcul du résultat net dans les états financiers.

D'autre part, les coûts implicites représentent la valeur des ressources que l'entreprise a choisies de ne pas utiliser pour une autre opportunité potentiellement rentable. Ces coûts sont souvent non monétaires et pourraient ne pas être évidents dans le bilan financier traditionnel d'une entreprise. Par exemple, si un propriétaire d'entreprise utilise un bâtiment qu'il possède pour son entreprise plutôt que de le louer à un tiers, le coût implicite est le loyer potentiel perdu, ou le revenu qu'il aurait pu générer. De même, si le propriétaire consacre son propre temps à l'entreprise, le coût implicite peut être le salaire qu'il aurait pu gagner en travaillant ailleurs.

L'approche économique reconnaît que les coûts implicites, tout comme les coûts explicites, sont réels et affectent le profit économique de l'entreprise. La prise en compte des coûts implicites permet de calculer le profit économique, qui est souvent inférieur au profit comptable en raison de l'inclusion de ces coûts non monétaires. Le profit économique est une mesure plus complète de la rentabilité, car il reflète le coût total des opportunités sacrifiées pour produire un bien ou un service.

Pour maximiser son profit économique, une entreprise doit donc considérer à la fois les coûts explicites et les coûts implicites, assurant ainsi qu'elle utilise ses ressources de la manière la plus efficace par rapport à toutes les options disponibles. C'est cette analyse globale qui éclaire les décisions stratégiques et contribue à la gestion judicieuse des ressources de l'entreprise.

Exemples de coûts implicites

Les coûts implicites, souvent appelés coûts non comptabilisés ou coûts d'opportunité, sont des éléments essentiels pour évaluer la rentabilité réelle d'une entreprise. Les exemples que vous avez donnés illustrent parfaitement la nature des coûts implicites :

Le coût du capital propre investi dans l’entreprise : Lorsqu'un entrepreneur investit des fonds propres dans son entreprise, il renonce à l'intérêt ou au rendement qu'il aurait pu obtenir en investissant cet argent ailleurs, comme dans un compte d'épargne, des obligations, des actions, ou toute autre opportunité d'investissement. Le coût implicite ici est le rendement financier perdu. Pour une analyse économique complète, il faut considérer ce coût d'opportunité comme une dépense réelle, car il représente le coût réel du capital qui n'est pas disponible pour d'autres usages.
Le salaire que l’entrepreneur recevrait comme employé dans une autre activité : Si l'entrepreneur consacre son temps et son effort à son entreprise, il ou elle ne peut pas les allouer à un emploi rémunéré ailleurs. Le coût implicite est donc le salaire que l'entrepreneur aurait pu gagner en travaillant pour quelqu'un d'autre ou en s'engageant dans une autre activité professionnelle. Ce coût doit être pris en compte lors de l'évaluation de la rentabilité de l'entreprise, car il s'agit d'un revenu potentiel non réalisé.

Ces coûts implicites sont souvent difficiles à quantifier avec précision, car ils impliquent des estimations de ce que pourrait être une « meilleure » alternative. Néanmoins, ils sont cruciaux pour les décisions économiques car ils fournissent une mesure plus réaliste de la performance économique de l'entreprise. Ignorer les coûts implicites pourrait conduire à une évaluation surévaluée de la santé financière et du succès de l'entreprise, car le profit comptable pourrait sembler plus élevé que le profit économique réel après prise en compte de ces coûts. En somme, les coûts implicites jouent un rôle vital dans la prise de décisions économiques éclairées. Ils aident à évaluer si les ressources de l'entreprise sont utilisées de la manière la plus avantageuse possible et si l'entreprise génère un retour suffisant pour justifier ces coûts d'opportunité.

Analyse du Comptable vs économiste dans l'évaluation des coûts et des profits d'une entreprise

Le rôle du comptable et de l'économiste dans l'évaluation des coûts et des profits d'une entreprise diffère significativement en raison de leur approche respective des coûts implicites.

Le comptable se concentre sur les transactions financières concrètes et les flux de trésorerie. Il calcule le profit comptable en soustrayant les coûts explicites, qui sont les paiements monétaires effectués pour les opérations de l'entreprise, des revenus générés par la vente de biens ou de services. Les coûts explicites sont donc tous les coûts qui sortent directement de la trésorerie de l'entreprise et sont enregistrés dans les livres comptables : salaires payés, loyers, coûts des matières premières, intérêts sur les prêts, etc. Les coûts implicites, étant non monétaires et ne représentant pas de flux de trésorerie réel, ne sont pas pris en compte dans les états financiers traditionnels.

L'économiste, en revanche, inclut à la fois les coûts explicites et les coûts implicites dans son calcul pour obtenir ce qu'on appelle le profit économique. Cette approche est plus large car elle reconnaît que les ressources ont une valeur au-delà de leur coût monétaire direct. En incorporant les coûts d'opportunité, l'économiste mesure le coût réel de la production et le succès financier de l'entreprise en termes de la maximisation de la valeur plutôt que simplement de la maximisation des liquidités. Le profit économique est ainsi défini comme les revenus moins la somme des coûts explicites et des coûts implicites.

Cette distinction est cruciale car elle peut conduire à des interprétations très différentes de la performance financière d'une entreprise. Un profit comptable positif ne signifie pas nécessairement que l'entreprise est économiquement viable si, une fois les coûts implicites pris en compte, le profit économique s'avère être nul ou négatif. En conséquence, les décisions basées uniquement sur les données comptables peuvent parfois être trompeuses si l'on ne considère pas également les coûts d'opportunité des ressources employées.

Profit économique et profit comptable

La distinction entre profit économique et profit comptable est fondamentale dans l'analyse des performances d'une entreprise.

Le profit comptable est le résultat financier qui reste après avoir soustrait les coûts explicites des revenus totaux. C'est la figure qui est habituellement rapportée dans les états financiers d'une entreprise et celle sur laquelle les décisions d'affaires sont souvent basées. Il s'agit d'un indicateur de la rentabilité opérationnelle immédiate de l'entreprise.

Le profit économique, quant à lui, prend en compte à la fois les coûts explicites et les coûts implicites. Le profit économique est calculé en soustrayant de la recette totale non seulement les coûts explicites, mais aussi la valeur des coûts d'opportunité des ressources utilisées dans le processus de production. Cela inclut des éléments tels que le coût du capital propre et le salaire alternatif que l'entrepreneur pourrait gagner ailleurs. Le profit économique est donc une mesure de la rentabilité qui reflète l'efficacité globale avec laquelle une entreprise utilise toutes ses ressources, y compris celles pour lesquelles elle ne fait pas de paiement monétaire direct.

Étant donné que le profit économique inclut des coûts supplémentaires que le profit comptable n'intègre pas (les coûts d'opportunité), il est logique que le profit économique ne puisse jamais dépasser le profit comptable. Si tous les coûts d'opportunité sont nuls, alors le profit économique et le profit comptable seraient égaux. Cependant, en réalité, il y a presque toujours des coûts d'opportunité, ce qui fait que le profit économique est souvent inférieur au profit comptable.

Il est tout à fait possible pour une entreprise de présenter un profit comptable positif tout en ayant un profit économique nul. Cela peut se produire lorsque les coûts d'opportunité consommés par l'entreprise équivalent exactement au profit comptable. Dans une telle situation, bien que l'entreprise semble rentable d'un point de vue comptable, économiquement, elle ne fait que couvrir tous ses coûts, y compris ses coûts d'opportunité, sans générer de rendement réel sur ses ressources. C'est un état de « profit normal », où l'entreprise couvre juste ses coûts implicites et explicites, mais n'obtient aucun surplus ou gain économique véritable.

Cette comparaison visuelle met en contraste deux méthodes d'évaluation de la performance financière d'une entreprise : l'une selon le point de vue économique et l'autre selon le point de vue comptable.

D'un côté, le point de vue économique prend en compte une vision plus large de la rentabilité. Ce modèle décompose la recette totale en trois segments. En partant de la base, les coûts explicites sont les paiements directs pour des ressources telles que le travail, les matériaux et le loyer. Au-dessus de ceux-ci se trouvent les coûts implicites, qui représentent la valeur de ce à quoi l'entreprise a renoncé en utilisant ses ressources de la manière actuelle plutôt que la meilleure alternative disponible. Cela pourrait inclure, par exemple, le revenu potentiel d'un investissement que le capital propre de l'entreprise aurait pu gagner ailleurs, ou le salaire qu'un propriétaire pourrait percevoir en travaillant dans une autre entreprise. La section la plus haute, colorée en vert, illustre le profit économique, également appelé 'surprofit'. Il s'agit du montant restant une fois que tous les coûts, explicites et implicites, ont été soustraits de la recette totale. Ce profit économique est souvent beaucoup plus petit que le profit comptable, car il prend en considération une gamme plus large de coûts.

De l'autre côté, le point de vue comptable se concentre uniquement sur les transactions et les flux de trésorerie tangibles. Les coûts explicites sont soustraits de la recette totale pour déterminer le profit comptable, représenté dans la partie supérieure du graphique. Ce profit ne tient pas compte des coûts d'opportunité et tend donc à présenter une image plus optimiste de la santé financière de l'entreprise.

Le graphique met en lumière un concept important : un profit comptable positif ne signifie pas nécessairement que l'entreprise est économiquement profitable. Il est possible que, même si une entreprise affiche un profit comptable, elle puisse avoir un profit économique nul ou même négatif une fois que les coûts d'opportunité sont pris en compte. Cela peut conduire à une compréhension erronée de la véritable performance de l'entreprise, car le profit comptable surévalue sa rentabilité en ignorant les coûts d'opportunité.

Cette image illustre la nécessité pour les entreprises de prendre en considération non seulement leurs coûts et revenus immédiats mais aussi les coûts d'opportunité associés à leurs décisions économiques. Cela permet une évaluation plus précise de la performance financière et aide à assurer que les ressources sont allouées de la manière la plus efficace. Pour les décideurs et les analystes, cette distinction est essentielle pour faire des choix éclairés qui tiennent compte de la valeur totale que l'entreprise crée ou pourrait créer.

La fonction de production et les coûts totaux

La fonction de production et la fonction de coût total sont deux concepts étroitement liés dans l'analyse économique de la production d'une entreprise. La fonction de production établit un lien technique entre les quantités d'inputs utilisés et la quantité d'outputs produite. Cela reflète l'efficacité avec laquelle une entreprise transforme les intrants, tels que le travail, les matières premières, et le capital, en produits finis ou services. Cette relation est souvent représentée graphiquement et peut prendre différentes formes selon les technologies et les processus de production utilisés par l'entreprise.

La fonction de coût total, quant à elle, met en relation la quantité produite avec les coûts de production correspondants. Les coûts de production comprennent tous les coûts explicites et implicites associés à la fabrication des biens ou services. Les coûts totaux augmentent généralement avec la quantité produite, mais pas toujours de manière linéaire en raison de l'existence de coûts fixes qui ne changent pas avec la production et de coûts variables qui le font.

L'interaction entre la fonction de production et la fonction de coût total est fondamentale. Les contraintes techniques de la fonction de production, comme les lois de rendements décroissants, influencent directement les coûts totaux. Par exemple, si une entreprise augmente la quantité d'un input, la production peut initialement augmenter à un rythme croissant. Cependant, après un certain point, l'ajout de plus d'inputs peut entraîner une augmentation moins que proportionnelle de l'output en raison de la saturation de l'efficacité des inputs supplémentaires.

Les économistes utilisent la fonction de coût total pour comprendre comment les coûts varient avec les changements dans le niveau de production et pour identifier le niveau de production où les coûts moyens sont minimisés. Ceci est crucial pour la prise de décision en matière de tarification et de production. En identifiant le coût marginal de production – le coût de production d'une unité supplémentaire – les entreprises peuvent déterminer le prix de vente optimal et la quantité de production pour maximiser les profits.

Les fonctions de production et de coût total offrent donc une vue d'ensemble de l'efficacité de la production et de la structure des coûts d'une entreprise. La compréhension de leur interdépendance est essentielle pour l'analyse économique et pour la planification stratégique d'une entreprise.

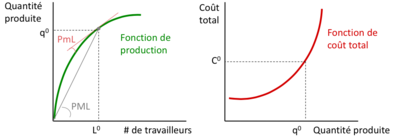
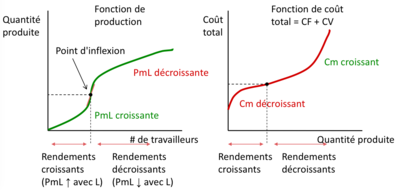
Ces deux graphiques distincts représentent un concept différent en économie de la production.

Le graphique de gauche décrit une fonction de production avec la quantité produite sur l'axe vertical et le nombre de travailleurs (qui est un input de production) sur l'axe horizontal. La courbe verte représente la fonction de production et montre comment la quantité produite augmente avec le nombre de travailleurs. La pente de la courbe en un point spécifique est représentée par PmL, qui signifie la productivité marginale du travail. C'est la contribution supplémentaire à la production de l'ajout d'une unité supplémentaire de travail. Au début, la courbe montre que la productivité marginale est en augmentation, ce qui est indiqué par la pente ascendante de la courbe de production. Cependant, à mesure que le nombre de travailleurs continue d'augmenter, la courbe s'aplatit, indiquant une diminution de la productivité marginale du travail. Cela peut être dû aux rendements décroissants, où l'ajout de travailleurs supplémentaires conduit à une augmentation moins que proportionnelle de la production car d'autres facteurs (comme les machines ou le capital) deviennent limitants.

Le graphique de droite représente la fonction de coût total avec le coût total sur l'axe vertical et la quantité produite sur l'axe horizontal. La courbe rouge indique que les coûts totaux augmentent avec la quantité produite. Initialement, la courbe monte lentement, reflétant les coûts fixes qui ne changent pas avec la production. À mesure que la production augmente, la courbe devient plus raide, reflétant l'augmentation des coûts variables. Le coût total comprend les coûts fixes plus les coûts variables multipliés par la quantité produite. Comme la courbe est en forme de J inversé, cela suggère que l'entreprise fait face à des rendements d'échelle croissants jusqu'à un certain point, après quoi elle expérimente des rendements d'échelle décroissants.

L'analyse de ces graphiques est cruciale pour la gestion d'entreprise. La fonction de production indique comment l'efficacité du travail affecte la quantité de biens ou de services qui peuvent être produits, tandis que la fonction de coût total montre comment ces niveaux de production se traduisent en coûts. La compréhension de ces relations aide les entreprises à optimiser leur niveau de production pour maximiser les profits. Par exemple, une entreprise pourrait chercher à produire à un niveau où la productivité marginale est élevée avant que les rendements décroissants ne commencent à se manifester, tout en surveillant les coûts totaux pour s'assurer que les coûts variables ne commencent pas à s'accroître de manière disproportionnée par rapport à la production.

Produit marginal et moyen du travail

Le produit marginal du travail (PmL) est un concept fondamental en économie qui décrit l'impact additionnel sur la production totale de l'ajout d'un travailleur supplémentaire, en supposant que tous les autres facteurs de production restent constants. C'est une mesure de l'efficacité marginale du travail dans le processus de production.

Mathématiquement, pour de petits accroissements, le produit marginal du travail peut être exprimé par le rapport de la variation de la quantité produite ( $\Delta q$ ) à la variation du travail ( $\Delta L$ ), ce qui donne la formule :

$PmL={\frac {\Delta q}{\Delta L}}$

Cette formule représente le taux de changement de la production par rapport au changement dans la quantité de travail utilisée, c'est-à-dire la pente de la fonction de production sur le graphique. Dans le cadre d'une analyse plus détaillée et précise, surtout quand on s'intéresse à des variations infiniment petites, le produit marginal du travail est représenté par la dérivée partielle de la quantité produite par rapport au travail, notée comme :

$PmL={\frac {\partial q}{\partial L}}$

Cette dérivée partielle donne la pente exacte de la fonction de production à un point donné et reflète l'augmentation de la production résultant de l'ajout d'une unité infinitésimale de travail.

Le concept de produit marginal est crucial pour comprendre comment les entreprises prennent des décisions relatives à la quantité de travail à employer. Théoriquement, une entreprise augmente la quantité de travail jusqu'au point où le produit marginal du travail égale le salaire réel, c'est-à-dire le coût de cette unité supplémentaire de travail. À ce point, l'entreprise maximise son profit, car engager un travailleur supplémentaire ne produirait pas assez de production supplémentaire pour couvrir le coût de son salaire.

Dans la pratique, l'entreprise recherche le niveau de production où le coût marginal de production (qui inclut le produit marginal du travail) est égal au revenu marginal afin de maximiser les profits. Cependant, divers facteurs tels que les changements technologiques, les ajustements du marché du travail et les réglementations peuvent influencer le produit marginal du travail et, par conséquent, la stratégie optimale de l'entreprise en matière de main-d'œuvre.

La fonction de production illustrée suggère que le produit marginal du travail (PmL) est décroissant, ce qui implique que l'ajout de travailleurs supplémentaires augmente la production mais dans des proportions de plus en plus petites. C'est une manifestation du principe des rendements décroissants, où l'efficacité de chaque travailleur additionnel diminue lorsque la quantité de travail augmente, en gardant les autres facteurs de production constants.

En termes mathématiques, cela signifie que la dérivée première de la fonction de production par rapport au travail, ${\frac {\partial q}{\partial L}}$ , diminue avec l'augmentation de L. Graphiquement, la pente de la courbe de production, qui représente le PmL, diminue à mesure que l'on se déplace le long de la courbe vers la droite, indiquant que chaque travailleur additionnel contribue moins à la production totale que le travailleur précédent.

Le produit moyen du travail (PML), d'autre part, est une mesure différente qui indique la production moyenne par travailleur. Il est calculé en divisant la production totale (q) par le nombre total de travailleurs (L), donné par la formule ${\frac {q}{L}}$ . Sur un graphique de la fonction de production, le PML est représenté par la pente d'un rayon partant de l'origine et allant jusqu'à un point spécifique sur la courbe de production. Ce rayon indique la production moyenne pour tous les niveaux de travail employés jusqu'à ce point.

Lorsque le nombre de travailleurs est faible, le PML peut augmenter à mesure que des travailleurs supplémentaires sont embauchés, car ils contribuent de manière significative à l'augmentation de la production. Toutefois, en vertu des rendements décroissants, il arrivera un point où l'ajout de nouveaux travailleurs commencera à diminuer le PML, car l'augmentation totale de la production sera moins importante que l'augmentation du nombre de travailleurs. Cela se produit lorsque le PmL est inférieur au PML.

La compréhension de ces indicateurs est cruciale pour les entreprises lorsqu'elles prennent des décisions relatives à l'emploi de travailleurs supplémentaires. Les entreprises chercheront à équilibrer le coût de l'ajout de travailleurs avec les bénéfices de la production supplémentaire pour maximiser l'efficacité et la rentabilité.

Les rendements décroissants

La Loi des rendements marginaux décroissants est un principe fondamental en économie qui décrit comment, après un certain point, chaque unité supplémentaire d'un facteur de production (dans ce cas, le travail) contribue moins à la production totale que la précédente, lorsque tous les autres facteurs de production sont maintenus constants. C'est une loi qui a d'importantes implications sur la productivité et la prise de décision en matière de production.

L'intuition derrière cette loi peut être comprise par un exemple simple : imaginez une cuisine avec un seul four et plusieurs cuisiniers. Au début, l'ajout de cuisiniers supplémentaires peut augmenter la production de repas car il y a suffisamment de travail pour chacun et le four est utilisé de manière optimale. Cependant, une fois que l'on a atteint le nombre optimal de cuisiniers dans la cuisine, l'ajout de plus de personnel ne fera pas cuire les repas plus rapidement car le four devient un goulot d'étranglement. Les cuisiniers supplémentaires peuvent même se gêner mutuellement, ce qui peut entraîner une diminution de l'efficacité globale.

Appliqué au contexte plus large de la production économique, cela signifie que si une entreprise continue d'ajouter de la main-d'œuvre à une quantité fixe d'autres ressources (comme les machines, les bâtiments ou la technologie), la contribution additionnelle de chaque nouveau travailleur va diminuer. Les premiers travailleurs peuvent utiliser efficacement les machines et l'espace disponible, mais les travailleurs suivants auront moins de machines à utiliser et moins d'espace pour travailler, ce qui réduit leur productivité marginale.

Cette loi explique pourquoi les entreprises ne peuvent pas simplement augmenter indéfiniment leur production en ajoutant plus de travailleurs. Au lieu de cela, elles doivent trouver un équilibre entre le nombre de travailleurs et la quantité d'autres ressources à leur disposition. Pour augmenter la production au-delà d'un certain point, une entreprise devra investir dans d'autres facteurs de production, comme l'achat de machines supplémentaires ou l'expansion des installations, plutôt que de se fier uniquement à l'ajout de main-d'œuvre.

Lorsque les travailleurs se retrouvent à devoir partager des ressources limitées comme des ordinateurs ou des photocopieuses, l'efficacité individuelle commence à décliner. Ce déclin se manifeste d'abord par de petites inefficacités, telles que l'attente pour utiliser l'équipement, mais peut rapidement s'intensifier en problèmes plus significatifs de coordination et de communication à mesure que davantage de travailleurs sont ajoutés. Les retards s'accumulent, les travailleurs passent plus de temps à attendre qu'à produire, et la frustration peut entraîner une baisse du moral, affectant encore plus la productivité.

Graphiquement, cela se traduit par une fonction de production qui, après un certain point, s'aplatit à mesure que la quantité de travail augmente, reflétant une diminution de la productivité marginale. Chaque travailleur supplémentaire ajoute moins à la production totale que le travailleur qui l'a précédé. Le graphique de la fonction de coût total révèle l'impact financier de cette loi : à mesure que la production augmente, les coûts marginaux - le coût de la production d'une unité supplémentaire - commencent également à augmenter. Cela est dû au fait que, si la production requiert plus de travail pour chaque unité supplémentaire en raison de la congestion des ressources, alors les coûts de production de cette unité supplémentaire vont inévitablement augmenter.

Dans la réalité, les entreprises peuvent rencontrer ce problème lorsque leur taille atteint un point où les ressources commencent à devenir rares par rapport au nombre d'employés. La solution pour éviter cet écueil n'est pas toujours d'ajouter plus de ressources, mais peut également impliquer une meilleure gestion des ressources existantes, une amélioration des processus de travail ou l'investissement dans des technologies qui améliorent l'efficacité.

L'intuition sous-jacente à la loi des rendements marginaux décroissants et son impact sur les coûts est que l'efficacité et la rentabilité peuvent souffrir si une entreprise ne parvient pas à équilibrer correctement son utilisation de la main-d'œuvre avec les autres ressources à sa disposition. Cela souligne l'importance d'une gestion stratégique des ressources pour optimiser la production et contrôler les coûts dans un environnement de production donné.

Exemple : fonction de production et coût total

L'exemple ci-dessous démontre la fonction de production et la structure des coûts d'un producteur de pizzas en fonction du nombre de travailleurs engagés. Lorsque l'atelier de pizza n'emploie aucun travailleur, il n'y a naturellement aucune production, et le coût total est purement constitué du coût fixe de l'atelier, qui s'élève à 30. Cette somme est probablement représentative des frais tels que le loyer, les services publics et l'amortissement de l'équipement, qui sont invariables quel que soit le niveau d'activité.

Fonction de production et de coût total d'un producteur de pizzas.

En introduisant le premier travailleur, la production commence à 50 pizzas, indiquant une contribution significative de ce travailleur unique à l'entreprise. Le coût total monte modestement à 40, incorporant le coût fixe de l'atelier plus un coût variable supplémentaire de 10 pour le travail. Ce coût supplémentaire représente le salaire ou la rémunération du travailleur.

Avec chaque travailleur supplémentaire ajouté, la production de pizzas augmente, mais il est intéressant de noter que l'augmentation de la production diminue à chaque fois, passant de 40 pizzas supplémentaires avec le premier travailleur à seulement 10 pizzas supplémentaires avec le quatrième travailleur. Cela illustre la loi des rendements marginaux décroissants, où chaque travailleur additionnel apporte une contribution de moins en moins importante à la production globale, probablement en raison de la limitation des ressources partagées comme l'espace de travail ou les équipements de cuisine.

Simultanément, bien que le coût fixe de l'atelier reste constant, le coût total du travail augmente de manière linéaire avec l'ajout de chaque nouveau travailleur. Cette progression linéaire est le résultat de l'ajout du coût du travail pour chaque nouveau travailleur, supposant que chaque travailleur coûte le même montant, indépendamment de la production réalisée.

Enfin, le coût total de la production, qui est la somme des coûts fixes et variables, grimpe à chaque ajout de travailleur, reflétant la hausse des coûts de production. Cependant, compte tenu de la baisse de la productivité marginale, le coût de production d'une unité supplémentaire augmente également, signifiant que l'entreprise doit dépenser plus pour chaque pizza supplémentaire produite au-delà d'un certain point. Cela suggère que, bien que l'ajout de main-d'œuvre puisse augmenter la production, cela se fait à un coût marginal croissant, un facteur que les entreprises doivent gérer soigneusement pour maintenir la rentabilité.

Cette analyse souligne l'importance de l'optimisation du nombre de travailleurs dans la production. Un producteur de pizzas, ou toute entreprise, doit identifier le nombre optimal de travailleurs qui maximisent la production sans entraîner de coûts disproportionnés en raison des rendements marginaux décroissants. Cela nécessite une compréhension attentive des coûts fixes et variables et de leur impact sur le coût total et la profitabilité de l'entreprise.

Fonction de production.

Ce graphique représente la fonction de production qui montre la relation entre le nombre de travailleurs embauchés et la quantité de pizzas produites par heure par un producteur de pizzas. Le graphique affiche une courbe typique de la production qui initialement monte rapidement à mesure que les travailleurs sont ajoutés, mais qui commence à s'aplatir après l'embauche d'un certain nombre de travailleurs, indiquant une diminution de la productivité marginale.

Au début, avec l'ajout des premiers travailleurs, l'augmentation de la production est substantielle pour chaque travailleur supplémentaire, illustrant une productivité marginale élevée. Cela peut être dû à une utilisation plus efficace des équipements et à une spécialisation du travail qui permet une augmentation significative de la production.

Cependant, le graphique montre également que, après l'ajout de quelques travailleurs, la production continue de croître mais à un rythme plus lent. Cela se produit parce que chaque travailleur additionnel contribue moins à la production globale que le précédent, un phénomène qui est le reflet de la Loi des rendements marginaux décroissants. Cette loi suggère qu'il y a un point optimal de travail au-delà duquel l'efficacité de chaque travailleur supplémentaire commence à décliner, souvent en raison du partage des ressources limitées ou de l'encombrement.

Le graphique indique que l'embauche du quatrième et du cinquième travailleur, par exemple, augmente la production mais à un taux décroissant par rapport aux premiers travailleurs. Cela peut être interprété comme un signe que l'espace de travail, les fours à pizza ou d'autres équipements deviennent des contraintes, et que l'ajout de travailleurs supplémentaires ne peut pas être entièrement exploité.

Pour le producteur de pizzas, ce graphique est essentiel pour déterminer le nombre optimal de travailleurs à embaucher afin de maximiser la production sans encourir des coûts inutiles pour des gains de production marginaux. En analysant où la courbe commence à s'aplatir, le producteur peut identifier le point de rendement décroissant et ainsi prendre des décisions éclairées sur la taille de la main-d'œuvre à maintenir pour une efficacité optimale.

Courbe de coût total.

La courbe de coût total illustrée dans l'image représente la relation entre la quantité produite (pizzas par heure) et le coût total en euros. La courbe démontre une progression ascendante qui s'intensifie à mesure que la production augmente, ce qui est typique dans les fonctions de coût total où les coûts varient en fonction de la production.

La partie initiale de la courbe monte relativement lentement, ce qui suggère que les coûts fixes dominent lorsque la production est faible. Les coûts fixes sont des dépenses qui ne changent pas avec le niveau de production, comme le loyer de l'atelier, le coût des équipements, et peut-être un salaire de base pour les employés. Par conséquent, lorsque le nombre de pizzas produites est faible, l'augmentation du coût total est modérée parce que les coûts variables (tels que les ingrédients pour les pizzas et les coûts marginaux du travail) sont encore minimes.

À mesure que la production augmente, la courbe s'élève plus abruptement. Cela indique que les coûts variables commencent à avoir un impact significatif sur le coût total. Les coûts variables peuvent inclure des dépenses supplémentaires pour les ingrédients, l'énergie utilisée pour cuire plus de pizzas, et les salaires supplémentaires pour les travailleurs embauchés pour augmenter la production. Cet aspect de la courbe est conforme à la loi des rendements marginaux décroissants ; à mesure que la production s'accroît, les coûts marginaux de production de chaque pizza supplémentaire augmentent en raison de l'utilisation moins efficace des ressources à mesure que l'atelier se rapproche ou dépasse sa capacité optimale de production.

La forme de la courbe suggère que la production de chaque pizza supplémentaire coûte plus cher que la précédente, indiquant des rendements d'échelle décroissants dans cette plage de production. C'est une considération importante pour le producteur de pizzas lors de la planification de l'expansion de la production. S'il continue à augmenter la production, le coût par unité continuera d'augmenter, ce qui pourrait finalement réduire les bénéfices.

Pour maximiser la rentabilité, le producteur doit trouver le niveau de production où le coût total est le plus faible par unité produite. Cela implique d'atteindre un équilibre entre les coûts fixes et variables et d'éviter de produire au-delà du point où les coûts marginaux commencent à dépasser les revenus marginaux. La courbe de coût total est un outil essentiel pour identifier ce point et prendre des décisions éclairées sur la quantité à produire.

Différentes mesures de coût

Coûts fixes

Les coûts fixes (CF) représentent les dépenses qu'une entreprise doit couvrir indépendamment de sa production. Ces coûts restent constants sur une période donnée même si la quantité de biens ou de services produits varie. Les coûts fixes sont souvent associés à des investissements en capital physique, tels que l'achat ou la location d'équipements et de bâtiments, qui ne changent pas en fonction de la production ou des ventes de l'entreprise.

Dans le cas d'un producteur de pizzas, les coûts fixes pourraient inclure la location de l'espace commercial, l'achat ou la dépréciation des fours à pizza et du matériel de cuisine, les salaires des employés qui sont garantis indépendamment du nombre de pizzas vendues, l'assurance, et peut-être certains services publics comme l'eau ou l'abonnement internet. Par exemple, que le producteur de pizzas fabrique 10 pizzas ou 100 pizzas, le loyer du local restera le même pour la période concernée. De même, l'achat d'un four à pizza est un coût initial qui ne change pas, que le four soit utilisé pour cuire une pizza ou utilisé continuellement.

Il est crucial pour les entreprises de comprendre et de gérer leurs coûts fixes, car ceux-ci constituent une partie importante de la structure des coûts totaux et peuvent influencer les décisions relatives aux prix, à la stratégie de production et à la viabilité à long terme. Un niveau élevé de coûts fixes peut également augmenter le risque financier de l'entreprise, car ces coûts doivent être couverts indépendamment des revenus. Les entreprises doivent donc générer suffisamment de revenus pour couvrir non seulement les coûts variables mais aussi ces coûts fixes afin d'éviter des pertes.

Coûts variables

Les coûts variables (CV) dans le cadre de la production d'une entreprise sont ceux qui fluctuent en fonction du volume d'activité ou de production. Contrairement aux coûts fixes, qui restent constants quel que soit le niveau de production, les coûts variables changent directement avec la quantité de biens ou de services produits.

Dans l'exemple d'un producteur de pizzas, les coûts variables comprennent les ingrédients nécessaires pour faire les pizzas, tels que la farine, la sauce tomate, le fromage, les garnitures, et aussi les coûts de l'énergie consommée pour faire fonctionner les fours et autres équipements de cuisine. En outre, si les travailleurs sont payés à l'heure ou à la pièce, alors leurs salaires sont également des coûts variables, car la main-d'œuvre totale requise variera en fonction du nombre de pizzas produites.

Si le producteur fabrique plus de pizzas, il aura besoin de plus d'ingrédients et peut-être d'heures de travail supplémentaires, ce qui augmentera ses coûts variables. Inversement, s'il décide de réduire la production, ses coûts variables diminueront car il utilisera moins d'ingrédients et moins de main-d'œuvre.

Les coûts variables sont essentiels à la gestion de l'entreprise car ils affectent directement la marge bénéficiaire par unité vendue. Une compréhension claire des coûts variables est nécessaire pour établir des stratégies de tarification efficaces et pour prendre des décisions concernant les niveaux de production optimaux. En contrôlant et en réduisant les coûts variables, une entreprise peut augmenter sa marge sur chaque produit vendu, ce qui est crucial pour la rentabilité globale. De même, lors de l'évaluation de la rentabilité d'un nouveau produit ou service, une analyse approfondie des coûts variables associés est fondamentale pour s'assurer que le prix de vente couvre ces coûts et contribue positivement au profit global.

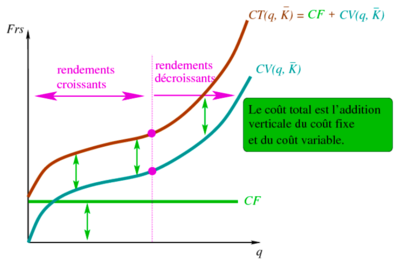
Coût total

Le coût total (CT) est effectivement la somme du coût fixe (CF) et du coût variable (CV). Cette relation est fondamentale pour comprendre la structure des coûts d'une entreprise et est exprimée mathématiquement comme suit :

CT = CF + CV

Cette équation illustre que pour chaque niveau de production, le coût total est composé d'une partie qui ne change pas, représentée par les coûts fixes, et d'une partie qui fluctue avec le niveau de production, représentée par les coûts variables. Les coûts fixes sont des dépenses qui doivent être payées indépendamment du volume de production, comme le loyer, les salaires des employés permanents, les paiements de prêts, et l'amortissement des équipements. Les coûts variables varient en fonction de la production, tels que les matières premières, les fournitures, et les heures de travail payées à la production.

Par exemple, si un producteur de pizzas a des coûts fixes mensuels de 2000 euros pour le loyer, les équipements et les salaires fixes, et des coûts variables de 2 euros par pizza pour les ingrédients et l'énergie, le coût total pour produire 1000 pizzas sera calculé en ajoutant le coût fixe au coût variable total pour cette production :

CT = CF + (CV par pizza × nombre de pizzas)

CT = 2000 + (2 × 1000)

CT= 2000 + 2000

CT=4000 euros

La compréhension du coût total est cruciale pour la prise de décision en matière de tarification et de niveau de production. En connaissant le coût total, une entreprise peut déterminer le prix de vente minimum nécessaire pour couvrir tous ses coûts et pour générer un profit. De plus, en analysant comment le coût total varie avec les changements dans le niveau de production, les entreprises peuvent identifier le point de production le plus efficace et maximiser leur rentabilité.

Coût moyen

Le coût moyen (CM), également connu sous le nom de coût unitaire, est une mesure qui permet de comprendre le coût de production par unité de bien ou de service produit. Il est dérivé en divisant le coût total (CT) par la quantité totale produite (q). Cette relation est représentée par la formule suivante :

$CM={\frac {CT}{q}}$

Étant donné que le coût total est la somme des coûts fixes et des coûts variables, le coût moyen peut également être exprimé en tant que somme du coût fixe moyen (CFM) et du coût variable moyen (CVM), où le coût fixe moyen est le coût fixe par unité produite et le coût variable moyen est le coût variable par unité produite. Ainsi, le coût moyen est également représenté par la formule :

$CM={\frac {CF}{q}}+{\frac {CV}{q}}$

Cela signifie que pour chaque unité produite, une portion du coût fixe et une portion du coût variable sont attribuées. Le coût moyen permet aux entreprises de déterminer le coût de fabrication de chaque unité de produit, ce qui est crucial pour fixer des prix de vente appropriés et pour évaluer l'efficacité de la production.

Par exemple, si un producteur de pizzas a un coût fixe de 2000 euros et produit 1000 pizzas, le coût fixe moyen par pizza est de 2 euros (2000 euros / 1000 pizzas). Si les coûts variables totaux pour ces 1000 pizzas sont de 2000 euros, le coût variable moyen par pizza est également de 2 euros (2000 euros / 1000 pizzas). Le coût moyen pour chaque pizza serait donc de 4 euros (2 euros de CFM + 2 euros de CVM), avant de prendre en compte la marge bénéficiaire.

Comprendre le coût moyen est particulièrement important pour la stratégie de tarification. Si le coût moyen est inférieur au prix de vente par unité, l'entreprise réalise un profit sur chaque unité vendue. Si le coût moyen est supérieur au prix de vente, l'entreprise subit une perte sur chaque unité. Ainsi, l'objectif est souvent de réduire le coût moyen, soit en réduisant les coûts, soit en augmentant la production pour mieux répartir les coûts fixes sur un plus grand nombre d'unités, ce qui réduit le coût fixe moyen.

Coût marginal

Le coût marginal (Cm) joue un rôle crucial dans l'analyse économique de la production, car il mesure l'impact sur le coût total d'une entreprise résultant de la production d'une unité supplémentaire d'un bien ou d'un service. C'est essentiellement la pente de la fonction de coût total à un point donné, représentant l'augmentation du coût total pour chaque augmentation unitaire de la production.

Mathématiquement, le coût marginal est défini comme le rapport entre la variation du coût total ( $\Delta CT$ ) et la variation de la quantité produite ( $\Delta q$ ). La formule est la suivante :

$Cm={\frac {\Delta CT}{\Delta q}}$

Lorsqu'on examine de très petits changements dans la quantité produite, le coût marginal peut être exprimé comme la dérivée du coût total par rapport à la quantité. Pour des changements infinitésimaux, la formule est :

$Cm={\frac {\partial CT}{\partial q}}$

Le coût marginal est particulièrement important dans la prise de décision en matière de production et de tarification. Les entreprises chercheront à produire jusqu'au point où le coût marginal est égal au revenu marginal, qui est le revenu additionnel obtenu de la vente d'une unité supplémentaire. Ce point est crucial car il correspond au niveau de production où les profits sont maximisés. Si le coût marginal est inférieur au prix de vente de l'unité supplémentaire, il est bénéfique pour l'entreprise d'augmenter la production. Inversement, si le coût marginal dépasse le prix de vente, produire davantage réduirait le profit de l'entreprise.

En pratique, l'analyse du coût marginal aide les entreprises à ajuster leur niveau de production pour répondre aux changements de la demande du marché, aux variations des coûts des inputs ou à l'introduction de nouvelles technologies, tout en visant à optimiser l'efficacité et la rentabilité.

Exemple

Ce tableau dresse le profil des coûts de production d'un producteur de limonade. Il montre la relation entre le nombre de verres de limonade produits par heure et différents types de coûts : coût total, coût fixe, coût variable, ainsi que les coûts moyens et marginaux associés.

Coûts de production d’un producteur de limonade

Le coût fixe reste constant à 3,00 euros, ce qui suggère qu'il s'agit de coûts qui ne dépendent pas du volume de production, comme le loyer ou l'amortissement des équipements. Le coût total commence à 3,00 euros lorsque aucun verre n'est produit et augmente avec la production. La différence entre le coût total à chaque étape et le coût fixe donne le coût variable, qui augmente avec le nombre de verres produits.

Les coûts fixes moyens (CFM) sont calculés en divisant le coût fixe par le nombre de verres produits. Étant donné que le coût fixe est constant, le CFM diminue à mesure que le volume de production augmente. Inversement, le coût variable moyen (CVM) est obtenu en divisant le coût variable total par le nombre de verres produits. Le coût moyen total (CM) représente la somme du CFM et du CVM et diminue d'abord avant d'augmenter légèrement, ce qui suggère qu'il pourrait y avoir une plage de production optimale où les coûts moyens sont minimisés.

Le coût marginal (Cm) représente le coût d'un verre supplémentaire et est obtenu en examinant la variation du coût total divisée par la variation de la quantité produite. Il commence à 0,30 euros et augmente progressivement, indiquant que chaque verre supplémentaire coûte plus cher à produire que le précédent. Cela reflète les rendements marginaux décroissants, où les coûts supplémentaires de production augmentent après un certain point à cause, par exemple, de la surutilisation des équipements ou de la nécessité d'embaucher plus de main-d'œuvre à un tarif plus élevé pour maintenir la production.

Cet ensemble de données permet au producteur de limonade de comprendre ses structures de coûts et de prendre des décisions éclairées sur la tarification et le niveau de production. Par exemple, en identifiant le point où le coût moyen total commence à augmenter, le producteur peut déterminer la quantité de production la plus efficace pour maximiser les profits. De plus, en comprenant le coût marginal, le producteur peut décider jusqu'à quel point il est rentable de continuer à augmenter la production.

Exemple : coût total

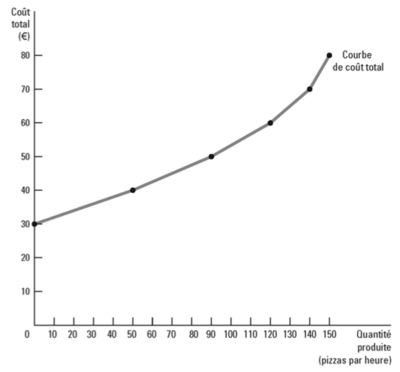
Ce graphique montre une courbe de coût total tracée en fonction de la quantité de pizzas produites par heure. La courbe montre une relation positive entre le coût total et le nombre de pizzas produites, indiquant que le coût total augmente avec la production.

Au début, la courbe semble augmenter à un rythme relativement constant, ce qui pourrait indiquer que les coûts variables dominent les coûts totaux après que les coûts fixes ont été couverts. Cela est cohérent avec le comportement typique des coûts variables qui augmentent proportionnellement avec la quantité produite. À mesure que la production augmente, nous pouvons observer que la pente de la courbe devient plus raide. Cela suggère que le coût de production de chaque pizza supplémentaire augmente, ce qui peut être dû à plusieurs facteurs, comme les rendements marginaux décroissants où l'ajout de plus de travail ou d'autres ressources ne se traduit pas par une augmentation proportionnelle de la production.

La pente croissante de la courbe de coût total peut également refléter le fait que l'entreprise a atteint sa capacité de production optimale et que produire des pizzas supplémentaires nécessite des investissements disproportionnés dans les intrants. Par exemple, si la capacité du four est maximisée, la production de pizzas supplémentaires pourrait nécessiter l'utilisation d'un four supplémentaire ou le passage à des heures supplémentaires pour le personnel, ce qui augmenterait le coût par unité.

L'analyse de cette courbe est essentielle pour la prise de décision en matière de gestion de production. Elle peut aider le producteur à identifier le niveau de production le plus rentable et à évaluer si les coûts actuels sont soutenables à long terme. Si la tendance de la courbe se maintient, le producteur pourrait avoir besoin de reconsidérer son processus de production, d'investir dans des équipements plus efficaces, ou de réajuster sa stratégie de tarification pour s'assurer que les coûts croissants ne grèvent pas les bénéfices.

Exemple : coût marginal

Le coût marginal reflète effectivement l'augmentation du coût total due à la production d'une unité supplémentaire d'un bien ou service. Dans un contexte de productivité décroissante, caractéristique de la loi des rendements marginaux décroissants, le coût marginal tend à augmenter à mesure que la quantité produite s'accroît. Cela se produit parce que chaque unité supplémentaire nécessite plus d'inputs ou d'efforts pour être produite, en raison des contraintes de capacité ou de l'inefficacité accrue des facteurs de production supplémentaires.

Étant donné que le coût fixe (CF) reste constant quel que soit le niveau de production, toute augmentation du coût total lorsqu'une unité supplémentaire est produite est due à une augmentation du coût variable (CV). Ainsi, le coût marginal est une mesure directe de la variation du coût variable. Mathématiquement, cela peut être exprimé comme suit:

$Cm={\frac {\Delta CV}{\Delta q}}$

Cela implique que le coût marginal est égal à la pente de la courbe des coûts variables par rapport à la quantité produite. Dans la pratique, cela signifie que si le coût de production de la prochaine pizza (par exemple) est plus élevé que celui de la pizza précédente, cela est dû aux coûts variables qui augmentent, comme la main-d'œuvre supplémentaire nécessaire ou les coûts de matériaux supplémentaires qui sont engagés pour maintenir la production.

Pour les entreprises, comprendre le coût marginal est essentiel pour prendre des décisions optimales en matière de production et de tarification. Produire au-delà du point où le coût marginal commence à dépasser le prix de vente peut réduire la profitabilité. Par conséquent, les entreprises visent généralement à ajuster leur niveau de production pour maintenir le coût marginal aussi bas que possible tout en satisfaisant la demande du marché.

Exemple : Coût moyen

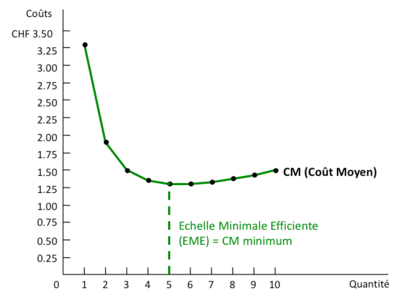
Le coût moyen a généralement une forme en U, c’est-à- dire il diminue avec les quantités produites lorsqu’on commence à produire le bien (le CF est réparti sur un petit nombre d'unités seulement), mais pour des quantités plus grandes de production il augmente avec les quantités produites (à cause de l'incidence grandissante du CVM).

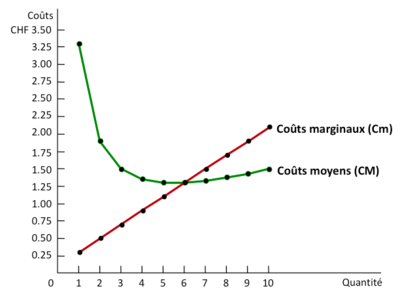
Coût marginal et coût moyen

Lorsque le coût marginal est supérieur au coût moyen, le coût moyen est croissant, alors qu’il est décroissant si le coût marginal lui est inférieur => Le coût marginal rencontre le coût moyen au minimum du coût moyen (EME).

Coût moyens (fixe et variable)

Plus en général

La productivité marginale est initialement croissante (spécialisation des travailleurs dans leurs tâches) et décroissante ensuite (car les facteurs fixes doivent être partagés par un nombre croissant de travailleurs)

Propriétés

Trois propriétés importantes des fonctions de coûts :

Le coût marginal va, tôt ou tard, finir par augmenter avec la quantité produite.
Le coût moyen a donc une forme en U (si le coût marginal était toujours décroissant on aurait des coûts moyens toujours décroissant également).
Le coût marginal croise la fonction de coût moyen à son minimum (ou à l’échelle minimale efficiente).

Résumé graphique

Exemple numérique

Une entreprise manufacturière a le coût total suivant :

CT(q)=100q-4q^{2}+0.2q^{3}+450

CF=450

CV(q)=100q-4q^{2}+0.2q^{3}

Cm(q)={\frac {\partial CT}{\partial q}}=100-8q+0.6q^{2}

CFM(q)={\frac {CF}{q}}={\frac {450}{q}}

CVM(q)={\frac {CV(q)}{q}}={\frac {100q-4q^{2}+0.2q^{3}}{q}}=100-4q+0.2q^{2}

CM(q)={\frac {CT(q)}{q}}={\frac {100q-4q^{2}+0.2q^{3}+450}{q}}=100-4q+0.2q^{2}+{\frac {450}{q}}=CFM+CVM

Lien entre fonction de production et coûts

La fonction de coût total est une sorte de fonction de production lue "à l'envers" (fonction réciproque):

Étant donné un certain stock de capital physique, on détermine quel est le nombre d'heures de travail nécessaires pour produire une certaine quantité q (= "envers" de la fonction de production);

On multiple ces heures de travail par le salaire horaire et on détermine ainsi la masse salariale 𝑤 ∙ 𝐿(𝐾, 𝑞) (= CV, si L est le seul input variable);

On rajoute à cela le coût fixe engendré par le capital physique pour obtenir le coût total.

Court versus long terme

Fonction de production de court et de long terme

Toute l'analyse qui précède a été faite en faisant implicitement l'hypothèse qu'un seul facteur de production, le travail, pouvait être adapté par l'entreprise afin de réaliser ses décisions de production. Ceci revient à dire que nous avons fait implicitement l'hypothèse que tous les inputs sauf le travail sont fixes. Autrement dit, nous avons fait une analyse de court terme.

Hypothèse : pour produire une certaine quantité q du bien, la firme utilise deux(mais on pourrait en considérer plus) inputs de production :

le capital physique, $K$
le travail, $L$

L’entreprise peut choisir différentes combinaisons de capital et de travail qui conduiront à différents niveau de production. La maximisation du profit sera maintenant une maximisation sur les deux quantités $L$ et $K$ .

Pour beaucoup de firmes, la répartition du coût total entre coûts fixes et coûts variables dépend de l’horizon temporel.

COURT TERME

Une entreprise qui doit décider au jour le jour quelle quantité produire considère sa capacité de production (= locaux, machines, instruments… = capital physique) comme donnée → fonction de production: $q=f({\bar {K}},L)$ .

LONG TERME

Quand elle planifie son activité future, l'entreprise peut décider de sa capacité de production → tous les inputs sont flexibles →fonction de production: $q=f(K,L)$ .

Coûts de production dans le court et long terme

Les coûts fixes sont liés au long terme ; les coûts variables sont des coûts modifiables sur le court terme.

La distinction entre coût variable et coût fixe dépend de l’horizon de temps qu’on considère:

dans le court terme certains coûts sont fixes (en général, les coûts liés au capital physique). On doit utiliser un stock de capital fixe
dans le long terme on peut rendre les coûts fixes variables notamment grâce aux investissements.
mais avec le temps ces mêmes coûts fixes deviennent variables car les entreprises peuvent ajuster leurs décisions sur tous les inputs (modification de la capacité physique de production).

Comme beaucoup de décisions sont fixes dans le court terme mais variables dans le long terme les fonctions de coût des entreprises ne sont pas les mêmes dans le court terme et dans le long terme.

Parce que beaucoup de décisions sont fixes dans le court terme mais variables dans le long terme, les coûts d’une firme sur le long terme diffèrent des coûts dans le court terme.

Il sera toujours plus facile d’avoir des coûts de production plus petits dans le long terme car on peut ajuster les facteurs de production qui sont fixes dans le court terme.

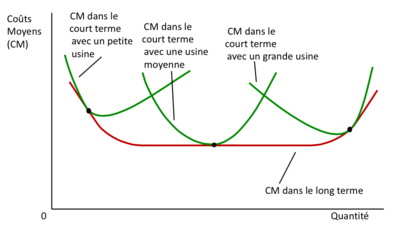
Les coûts moyens dans le court et long terme

Economies d’échelle

La pente de la fonction de CM à long terme nous indique la présence ou absence d’économies d’échelle.

Rendements marginaux vs rendements d'échelle

Ne pas confondre le concept de rendement marginal ou de produit marginal avec le concept de rendement d'échelle!

Le rendement marginal (souvent décroissant) est un concept de court terme: il nous indique la variation de l'output pour un changement d'un seul input, tous les autres étant fixes.

Le rendement d'échelle (croissant, constant, décroissant) est un concept de long terme : tous les inputs sont variables et une entreprise qui veut modifier ses décisions de production peut aussi intervenir sur sa capacité de production.

Intuition pour économies d'échelle (→ rendements d'échelle croissants) :

dans une usine plus grande beaucoup de tâches peuvent être agrégées + spécialisation plus élevée de K et de L possible + possibilité d’utiliser de la main d’œuvre qualifiée ou des machines plus performantes...

Intuition pour déséconomies d'échelle (→ rendements d'échelle décroissants) :

difficultés croissantes dans l’organisation et l’intégration des activités dans une usine de taille grandissante + moins d’engagement personnel des travailleurs + le management ne suit pas (sorte de « facteur fixe »)...

Résumé

L’objectif de l’entreprise est de maximiser le profit = différence entre la recette totale et le coût total.

Le coût total inclut les coûts explicites mais aussi les coûts implicites (= coûts d'opportunité de la production).

Le coût total de l’entreprise est un reflet de sa fonction de production.

Une fonction de production type montre généralement une productivité décroissante (en tout cas a partir d’une certaine quantité ou échelle de production).

Le coût total de l’entreprise est divisé entre les coûts fixes (qui ne changent pas avec la quantité produite) et les coûts variables (qui dépendent des quantités produites).

Le coût moyen est le coût total par unité produite.

Le coût marginal nous donne l’augmentation dans le coût total nécessaire à produire une unité additionnelle. Généralement augmente avec la quantité produite (en tout cas a partir d’une certaine quantité produite).

Si le coût marginal est croissant, le coût moyen doit, tôt ou tard, commencer à augmenter; il va donc d’abord diminuer et ensuite augmenter avec les quantités produites. Il aura une forme en U.

La courbe de coût marginal croise la fonction de coût moyen à son minimum (au point d’échelle minimum efficace).

La forme des fonctions de coût dépend de l’horizon de temps qu’on considère.

Beaucoup de coûts qui sont fixes dans le court terme deviennent variables dans le long terme.

Annexes

Références

[1] Page personnelle de Federica Sbergami sur le site de l'Université de Genève

[2] Page personnelle de Federica Sbergami sur le site de l'Université de Neuchâtel

[3] Page personnelle de Federica Sbergami sur Research Gate

[1]

[2]

[3]