« Oligopole » : différence entre les versions
Aucun résumé des modifications |
|||
| (46 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 29 : | Ligne 29 : | ||
}} | }} | ||
L'oligopole représente un type spécifique de concurrence imparfaite. Cette structure de marché se retrouve dans des secteurs où plusieurs entreprises sont en concurrence, mais sans que cette concurrence ne soit assez intense pour les transformer en "preneuses de prix". La particularité de l'oligopole est le nombre restreint d'acteurs impliqués, engendrant une compétition stratégique et minutieuse entre eux. | |||
{{Translations | Dans ce contexte, on distingue différents cas selon le nombre de participants sur le marché. Par exemple, un duopole implique deux entreprises tandis qu'un oligopole caractérise un marché avec quelques offreurs. Ces marchés, où le nombre de vendeurs est relativement petit, sont qualifiés de marchés concentrés. Cette concentration confère aux entreprises un certain pouvoir de marché, leur permettant de fixer les prix et souvent de pratiquer des tarifs supérieurs aux coûts de production. | ||
Les caractéristiques essentielles de l'oligopole incluent un équilibre délicat entre la coopération et la poursuite des intérêts individuels. Bien que ces entreprises aient le pouvoir d'influencer les prix, ce pouvoir est moindre comparé à un monopole. L'interdépendance des décisions des différents acteurs est un autre trait saillant, où chaque entreprise doit tenir compte des stratégies et actions des autres. La collusion, où les firmes coopèrent pour maximiser leurs profits collectifs, est une possibilité dans un tel marché. Enfin, la théorie des jeux, étudiant le comportement des individus dans des situations stratégiques, est particulièrement pertinente pour analyser le comportement des entreprises en situation d'oligopole, fournissant des insights sur{{Translations | |||
| en = | | en = | ||
| es = Oligopolio | | es = Oligopolio | ||
| Ligne 52 : | Ligne 41 : | ||
== Hypothèses == | == Hypothèses == | ||
L'analyse d'un marché sous les hypothèses énoncées révèle un cadre de marché oligopolistique avec des caractéristiques spécifiques. | |||
Premièrement, l'hypothèse d'atomicité du côté de la demande indique que les consommateurs sont nombreux et aucun d'entre eux n'a suffisamment de pouvoir pour influencer le prix du marché. Cette condition assure que le pouvoir de marché est principalement détenu par les offreurs. | |||
Deuxièmement, la nature homogène du bien implique que tous les produits offerts sur le marché sont identiques ou presque. Dans ce contexte, les entreprises ne peuvent pas se différencier par la qualité, le design ou d'autres caractéristiques du produit. Néanmoins, il est également possible d'avoir un oligopole avec des biens différenciés, connu sous le nom d'oligopole à la Bertrand, où la concurrence se fait principalement sur les prix. | |||
Troisièmement, l'absence de libre-entrée indique que de nouvelles entreprises ne peuvent pas facilement entrer sur le marché, souvent en raison de barrières à l'entrée telles que des coûts de démarrage élevés, des technologies propriétaires ou des réglementations gouvernementales. Cela maintient le nombre d'offreurs à un niveau fixe et faible. | |||
Les offreurs dans ce marché ont un pouvoir de marché significatif, leur permettant de fixer des prix supérieurs au coût marginal. Cela résulte du nombre limité de participants et de l'absence de produits de substitution parfaits. | |||
Enfin, étant donné que le bien est homogène, les stratégies des entreprises se concentrent principalement sur le volume de production. Elles n'engagent pas de dépenses en publicité, en différenciation des prix ou en amélioration de la qualité, car ces aspects ne sont pas pertinents dans un marché où les produits sont indifférenciés. | |||
Dans ce type de marché, les entreprises peuvent s'engager dans un comportement stratégique en ce qui concerne les volumes de production, potentiellement en se coordonnant pour maximiser les profits globaux. Les interactions entre les entreprises sont souvent analysées à l'aide de modèles de théorie des jeux, qui peuvent prédire des issues telles que la fixation de quantités de production pour maximiser les profits collectifs ou la compétition pour une part de marché plus importante. | |||
== La demande d'eau potable == | |||
Un exemple est un scénario de marché pour l'eau potable dans un village avec deux caractéristiques importantes : la demande d'eau et la structure du marché dictée par ses offreurs, UN et DEUX. | |||
La demande d'eau potable est décrite par la fonction <math>q^D = 120 - p</math>, où <math>q^D</math> est la quantité demandée et <math>p</math> est le prix. Cette fonction montre que la demande diminue à mesure que le prix augmente, ce qui est typique des marchés de biens courants. La forme inverse, <math>p = 120 - q</math>, est la fonction de volonté de payer, indiquant le prix maximal que les consommateurs sont prêts à payer pour une quantité donnée d'eau. | |||
Dans ce village, il y a deux fournisseurs uniques (UN et DEUX) pour l'eau potable. L'eau provient d'une source, et on suppose que le coût marginal de fourniture de cette eau est nul, ce qui signifie que le coût total (CT) est équivalent au coût fixe (CF). | |||
Dans ce cadre, il est intéressant d'examiner comment le prix et la quantité offerte seraient affectés sous deux structures de marché extrêmes : la concurrence parfaite et le monopole. | |||
Dans | |||
Concurrence Parfaite : Dans un marché de concurrence parfaite, de nombreux vendeurs et acheteurs participent au marché, et aucun d'entre eux n'a suffisamment de pouvoir pour influencer le prix du marché. Cependant, il n'y a que deux offreurs, ce qui ne correspond pas exactement à une concurrence parfaite. Néanmoins, si UN et DEUX agissaient comme en concurrence parfaite, ils prendraient le prix du marché comme donné et produiraient en fonction de la demande. Le prix se stabiliserait au coût marginal, qui est ici nul. | |||
Dans | Monopole : Dans un scénario de monopole, un seul vendeur contrôle l'ensemble du marché. Si UN et DEUX fusionnaient ou si l'un éliminait l'autre pour devenir le seul fournisseur, la structure du marché deviendrait monopolistique. Le monopoleur maximiserait les profits en fixant un prix où le revenu marginal est égal au coût marginal. Cependant, comme le coût marginal est nul, le monopoleur choisirait un prix et une quantité qui maximiseraient ses profits en tenant compte de la fonction de demande du marché <math>p = 120 - q</math>. | ||
Dans les deux cas, la dynamique du marché serait influencée par la manière dont UN et DEUX interagissent, soit en concurrence, soit en tant qu'entité monopolistique. | |||
== Solution en concurrence parfaite == | |||
Sous l'hypothèse de concurrence parfaite, le prix sur le marché s'aligne sur le coût marginal. Dans ce cas, comme le coût marginal de l'eau potable est zéro (<math>P = Cm = 0</math>), le prix serait également nul. À ce prix, la quantité totale consommée serait égale à la quantité totale demandée à un prix nul, soit <math>Q = 120</math>. Cet équilibre serait considéré comme efficient du point de vue de l'allocation des ressources, car le prix reflète exactement le coût marginal de production. | |||
Cependant, | Cependant, cette situation soulève un paradoxe pratique. Si l'eau est fournie gratuitement (<math>P = 0</math>), comment les deux fournisseurs, UN et DEUX, couvriraient-ils leurs coûts fixes et continueraient-ils à opérer? Dans la réalité, même si le coût marginal est nul, il existe des coûts fixes (comme l'entretien de l'infrastructure, les salaires, etc.) qui doivent être couverts pour assurer la viabilité économique des fournisseurs. | ||
Ce paradoxe met en évidence une limitation du modèle de concurrence parfaite dans ce contexte. La concurrence parfaite suppose un grand nombre d'offreurs et d'acheteurs, une information parfaite, une absence de coûts de transaction, et des produits homogènes. Mais dans ce scénario, avec seulement deux offreurs et des coûts fixes non nuls, le modèle de concurrence parfaite ne semble pas être le plus approprié pour décrire de manière réaliste le fonctionnement du marché. | |||
Ainsi, même si théoriquement, sous concurrence parfaite, le prix de l'eau serait nul et la quantité consommée maximale, dans la pratique, d'autres modèles de marché (comme l'oligopole ou le monopole) pourraient être plus pertinents pour analyser et comprendre le comportement des offreurs dans ce marché particulier. | |||
== Solution en monopole == | == Solution en monopole == | ||
Dans un monopole | Dans un régime de monopole où UN et DEUX coopèrent, la situation change radicalement par rapport à un marché en concurrence parfaite. Dans ce cas, le profit est maximisé quand la recette totale du marché est maximale, ce qui est particulièrement pertinent étant donné l'absence de coûts variables dans le scénario. | ||
La maximisation du profit dans un monopole est exprimée par la formule : <math>max \pi = RT - CT = (120 - q)q - CF</math>. Ici, π représente le profit, RT la recette totale, CT le coût total, q la quantité produite, et CF le coût fixe. | |||
Pour trouver le niveau de production qui maximise le profit, on dérive la fonction de profit par rapport à q et on égale le résultat à zéro. Cette condition première d'ordre (CPO) est donnée par <math>\frac{\partial \pi}{\partial q} = (120 - 2q) = 0</math>. En résolvant cette équation, on obtient <math>q^\ast = 60</math> et par conséquent, <math>p = 60</math>. Ainsi, la recette totale maximale et donc le profit maximal est <math>RT_{max} = \pi_{max} = 3600</math>. | |||
Dans ce cadre de coopération, UN et DEUX pourraient s'accorder pour vendre une quantité totale de 60 unités au prix de 60, se partageant la recette totale de 3600 à parts égales, soit 1800 chacun. | |||
En termes de stratégie de marché, cette coopération pourrait prendre la forme d'une collusion ou d'un cartel : | |||
* Collusion : Cela se produit lorsque les entreprises s'entendent secrètement sur les quantités à produire ou les prix à fixer. | |||
* Cartel : C'est quand des offreurs se regroupent formellement et agissent ensemble, souvent par un accord ouvert et officiel. | |||
Cependant, il est important de noter que, bien que les producteurs en situation d'oligopole puissent être tentés de former des cartels pour réaliser des profits de monopole, ces pratiques sont souvent réglementées ou interdites par les lois antitrust. Ces lois visent à prévenir la restriction de la concurrence et à protéger les intérêts des consommateurs, rendant les accords explicites entre producteurs en oligopole illégaux dans de nombreux pays. | |||
[[Fichier:Oligopole solution en monopole 1.png|400px|vignette|centré]] | |||
Ce graphique économique typique illustre la situation d'un monopole dans le contexte du marché de l'eau potable. Le graphique est divisé en deux sections principales : la courbe de demande (ou volonté de payer) sur le graphique supérieur, et la courbe de recette totale sur le graphique inférieur. | |||
Dans le graphique supérieur, la droite de demande décroît de gauche à droite, indiquant que moins d'eau sera demandée à mesure que le prix augmente, ce qui est cohérent avec la loi de la demande. Le prix du monopole est fixé à 60, ce qui est le point où la recette marginale (non représentée) serait égale au coût marginal, qui est de zéro dans ce cas. Cela est indiqué par le fait que la droite de demande coupe l'axe des quantités à 120 unités, le maximum que les consommateurs seraient prêts à acheter si l'eau était gratuite, et le prix maximum de 120, où la quantité demandée serait nulle. | |||
Le prix | Le graphique inférieur montre la recette totale (RT), qui est une parabole avec un sommet au point où la quantité est de 60, ce qui représente la quantité optimale pour le monopoleur à vendre. À ce niveau de production, la recette totale est maximisée à 3600, comme indiqué par le pic de la courbe de recette totale. C'est le résultat de la multiplication du prix par la quantité (60 unités x 60 de prix = 3600 de recette totale). | ||
Le commentaire sur le graphique indique que pour maximiser le profit, qui dans ce cas est égal à la recette totale en raison de l'absence de coûts variables, chaque entreprise devrait produire une quantité de 30 et obtenir un profit de 1800 chacune. Cela suppose que les deux entreprises coopèrent parfaitement, partageant le marché équitablement sous un accord de cartel. Cependant, cette situation pourrait ne pas être stable à long terme en raison de la tentation de tricher sur l'accord pour augmenter sa part du profit, un problème communément associé à la théorie des jeux dans l'étude des oligopoles et des cartels. | |||
Il est également important de noter que, bien que cette configuration puisse être profitable pour les monopolistes, elle n'est pas nécessairement bénéfique pour les consommateurs ni pour le bien-être social. Le prix de 60 est supérieur au coût marginal de l'eau (qui est zéro), et par conséquent, la quantité produite et consommée (60 unités) est inférieure à ce qu'elle serait dans un marché concurrentiel (120 unités). Cela conduit à une perte sèche, où certains consommateurs qui auraient été disposés à payer un prix supérieur au coût marginal n'ont pas accès à l'eau. | |||
Enfin, la législation antitrust serait un obstacle à un tel arrangement dans de nombreuses juridictions, car elle est conçue pour empêcher les entreprises de fixer des prix et de limiter la production de manière anticoncurrentielle. | |||
== Incitation à tricher == | |||
L'incitation à tricher dans un accord de cartel est un problème classique dans l'analyse économique des oligopoles. Dans l'exemple de UN et DEUX, même si les deux entreprises s'accordent initialement pour produire chacune 30 unités et fixer le prix à 60, chacune a une incitation à augmenter sa production secrètement pour capturer une plus grande part du marché. | |||
Si UN décide de produire plus tout en anticipant que DEUX maintiendra sa production à 30 unités, la demande résiduelle à laquelle UN fait face est alors donnée par la nouvelle fonction de demande <math>p_1 = 120 - q_2 - q_1 = 120 - 30 - q_1 = 90 - q_1</math>. Cela signifie que le prix que UN peut fixer diminue à mesure que sa propre quantité produite, <math>q_1</math>, augmente. | |||
La recette totale de UN est donnée par <math>RT_1 = (90 - q_1)q_1</math>, et la recette marginale est identique en l'absence de coûts marginaux, donc <math>Rm_1 = (90 - q_1)q_1</math>. Pour maximiser son profit, UN déterminerait la quantité de production où la recette marginale égale le coût marginal, ce qui mènerait à <math>q_1^\ast = 45</math>. | |||
En produisant 45 unités, UN augmente la quantité totale sur le marché à 75 unités (les 30 de DEUX plus ses 45), ce qui fait baisser le prix à 45 selon la fonction de demande du marché. Malgré la baisse du prix, UN améliore son revenu à <math>45^2 = 2025</math>, dépassant les 1800 qu'il aurait reçus en se conformant à l'accord de cartel. | |||
Ce scénario démontre la tentation de la triche dans les cartels. Si UN augmente sa production, il peut gagner plus à court terme. Cependant, si DEUX s'aperçoit de la triche de UN et décide également de produire plus, le prix du marché pourrait chuter considérablement, potentiellement au-dessous du niveau optimal pour les deux entreprises. La nature instable des cartels est due à cette incitation à tricher et à la difficulté de maintenir la discipline de cartel, surtout en l'absence de mécanismes d'application et de surveillance. En pratique, la plupart des cartels finissent par échouer à cause de cette incitation interne à la triche, à moins qu'ils ne soient soutenus par des mécanismes de contrôle stricts ou des régulations. | |||
[[Fichier:Oligopole incitation à tricher 1.png|400px|vignette|centré]] | |||
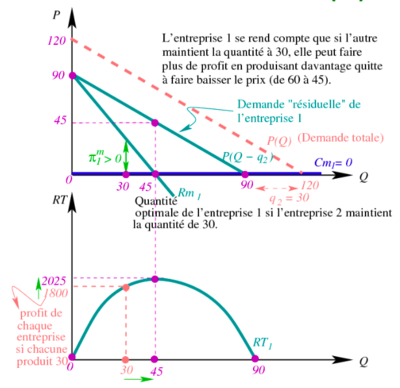
Ce graphique économique illustre la situation où l'entreprise UN envisage de tricher dans un accord de cartel avec l'entreprise DEUX pour le marché de l'eau potable. Le graphique supérieur montre la courbe de demande totale du marché, qui est une ligne droite descendant de 120 à 0 en fonction de la quantité. À côté, il y a une courbe de demande "résiduelle" pour l'entreprise UN, qui commence à 90 au lieu de 120, assumant que DEUX continue de produire 30 unités. | |||
L'entreprise UN réalise qu'en produisant plus que sa part convenue de 30 unités — spécifiquement 45 unités — tout en s'attendant à ce que DEUX continue à produire 30 unités, elle peut augmenter ses profits. La nouvelle quantité totale sur le marché serait de 75 unités, ce qui fait baisser le prix de 60 à 45. Bien que le prix soit plus bas, le profit de UN augmente, car il est calculé en fonction de la quantité qu'elle vend elle-même. Le graphique inférieur illustre la recette totale de UN avec un pic à 2025, qui est supérieur à la recette de 1800 obtenue si chaque entreprise respecte l'accord de produire 30 unités. | |||
La ligne pointillée verticale qui part de 45 unités sur le graphique supérieur et qui touche le point le plus haut de la courbe de recette totale de UN sur le graphique inférieur indique clairement que 45 unités est la quantité optimale pour UN si elle veut maximiser son profit en supposant que DEUX ne change pas sa quantité de production. Cependant, cette action de triche baisse le prix de marché pour les deux entreprises, ce qui signifie que DEUX verra son profit réduit à moins qu'elle ne réagisse. | |||
Cette situation illustre le dilemme central des cartels : bien qu'ils puissent être profitables lorsqu'ils sont respectés, chaque membre a une incitation individuelle à produire plus pour augmenter ses bénéfices personnels. Cela mine l'accord de cartel et peut conduire à son effondrement, avec des conséquences potentiellement négatives pour tous les participants. De plus, si DEUX remarque la triche de UN et décide d'augmenter également sa production, le prix sur le marché pourrait tomber encore plus bas, réduisant les profits pour les deux entreprises. | |||
La situation décrite est un exemple classique du "prisonnier's dilemme" en théorie des jeux, où les acteurs, bien que rationnels et poursuivant leur propre intérêt, aboutissent à un résultat qui n'est pas optimal pour le groupe. Cela démontre la difficulté de maintenir la coopération dans les accords de cartel, surtout en l'absence de mécanismes de surveillance et de punition pour la triche. | |||
== Équilibre sans coopération == | == Équilibre sans coopération == | ||
Dans une situation où il n'y a pas de coopération entre UN et DEUX, les deux entreprises entrent dans un cycle de réaction et contre-réaction en ajustant leur production en réponse aux actions de l'autre. Si UN triche en augmentant sa production et que DEUX s'en rend compte, DEUX peut choisir d'augmenter également sa production pour récupérer une partie de son profit perdu. Cette dynamique continue jusqu'à ce qu'un équilibre de duopole soit atteint. | |||
L'équilibre de duopole est défini par la condition où les recettes marginales des deux entreprises sont égales et où aucune n'a intérêt à changer sa quantité de production car cela ne ferait qu'abaisser leur profit marginal. Dans le cas présenté, les conditions d'équilibre de duopole sont exprimées par les équations <math>Rm_1 = 120 - q_2 - 2q_1 = Rm_2 = 120 - q_1 - 2q_2 = Cm = 0</math>. En résolvant ces équations, on obtient que les quantités optimales pour les deux entreprises sont <math>q_1^{*} = q_2^{*} = 40</math>. Le prix se stabilise alors à <math>p = 40</math> et les recettes totales pour chacune des entreprises sont <math>RT_1 = RT_2 = 1600</math>. | |||
À cet équilibre, les deux entreprises produisent chacune 40 unités et le prix du marché est de 40. Cela se traduit par un profit de 1600 pour chaque entreprise, ce qui est inférieur au profit qu'elles auraient pu réaliser si elles avaient maintenu l'accord de cartel et coopéré pour maintenir le prix à 60, générant ainsi un profit de 1800 chacune. | |||
Ce résultat illustre un aspect central des oligopoles : lorsque les entreprises ne coopèrent pas, elles finissent par être pénalisées par la concurrence qu'elles se font mutuellement. L'équilibre de duopole mène à un résultat où chaque entreprise gagne moins que ce qu'elle aurait pu obtenir dans un accord de cartel. Néanmoins, cet équilibre est plus stable que le cartel parce qu'il n'y a pas d'incitation à dévier unilatéralement, puisque toute tentative d'augmenter la production réduirait la recette marginale de l'entreprise concernée. | |||
L'équilibre de duopole reflète un compromis entre la concurrence et la coopération. Bien qu'il ne soit pas aussi profitable pour les entreprises qu'une collusion totale, il est conforme aux lois antitrust et tend à être plus avantageux pour les consommateurs, car il résulte en un prix inférieur et une quantité supérieure par rapport à ce qui serait observé sous un cartel. | |||
[[Fichier:Oligopole équilibre sans coopération 1.png|400px|vignette|centré]] | |||
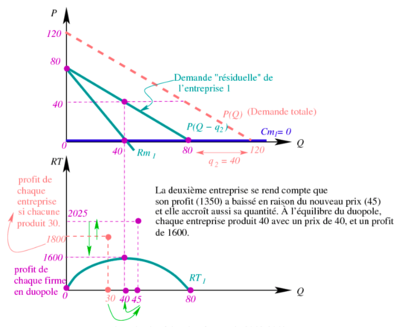
Ce graphique représente la continuation de l'analyse économique du marché de l'eau potable dans une situation de duopole sans coopération, où les entreprises UN et DEUX ajustent leur production en réponse aux actions de l'autre jusqu'à atteindre un équilibre. | |||
Le graphique supérieur montre les courbes de demande totale et résiduelle pour l'entreprise UN. La courbe de demande résiduelle démarre à un prix de 80 pour zéro quantité, supposant que DEUX produit 40 unités (comme indiqué par le point où la courbe résiduelle rencontre l'axe vertical). La courbe de demande totale décrit la volonté de payer pour l'ensemble du marché et décroît en fonction de la quantité totale. L'intersection de la quantité produite par UN et la demande résiduelle détermine le prix sur le marché. | |||
Le graphique inférieur illustre les recettes totales (RT) pour l'entreprise UN avec une courbe en forme de parabole, atteignant son sommet à 40 unités produites par UN, ce qui correspond à la recette totale et donc au profit maximal lorsque DEUX produit également 40 unités. Le profit de chaque entreprise dans le duopole est illustré par le niveau de 1600, inférieur au profit de 2025 pour UN lorsqu'elle a triché et produit 45 unités, mais plus élevé que le profit de 1350 de DEUX lorsque UN a produit 45 et DEUX est restée à 30. | |||
Le commentaire sur l'image indique que DEUX reconnaît que son profit a diminué en raison de la baisse du prix (à 45) lorsque UN a augmenté sa production, et donc DEUX augmente également sa production pour compenser. Finalement, les deux entreprises s'ajustent pour atteindre un équilibre où elles produisent chacune 40 unités, conduisant à un prix de marché de 40 et à un profit de 1600 pour chacune. | |||
Cette situation d'équilibre en duopole montre que, même si les entreprises pourraient potentiellement gagner plus en coopérant (comme dans le cartel où elles gagnaient 1800 chacune), la tentation de tricher et l'absence de mécanismes de coopération les conduisent à un résultat où elles gagnent moins. Cependant, cet équilibre est plus stable car aucun des duopolistes n'a d'incitation à changer sa production, puisque toute augmentation réduirait le prix et donc les profits. | |||
L'image illustre le concept d'équilibre de Nash dans le contexte d'un duopole, où chaque entreprise, en prenant en compte la stratégie de l'autre, choisit sa meilleure réponse. Cet équilibre n'est pas l'optimal de Pareto, car il y a une perte sèche due au fait que le prix est supérieur au coût marginal (qui est de zéro), et donc la quantité produite est inférieure à ce qu'elle serait dans un marché parfaitement concurrentiel. Cela révèle la tension intrinsèque dans les marchés oligopolistiques entre les incitations individuelles et le bien-être collectif. | |||
== Maximisation du profit en duopole : cas général == | |||
Dans un duopole, la maximisation du profit est un problème classique d'interaction stratégique entre deux entreprises. Chaque entreprise cherche à maximiser ses profits en tenant compte non seulement de ses propres coûts et de la demande du marché, mais également des actions de son concurrent. | |||
Pour l'entreprise 1, la maximisation du profit est donnée par l'équation <math>max_{q1} \pi_1 = p(Q)q_1 - CT(q_1)</math>, où <math>q_1</math> est la quantité produite par l'entreprise 1, <math>p(Q)</math> est le prix du marché en fonction de la quantité totale <math>Q</math> offerte sur le marché, et <math>CT(q_1)</math> sont les coûts totaux de l'entreprise 1. Ici, <math>Q</math> est la somme des quantités produites par les deux entreprises, soit <math>Q = q_1 + q_2</math>. | |||
La condition de premier ordre (CPO) pour la maximisation du profit pour l'entreprise 1, où la recette marginale <math>Rm_1</math> est égale au coût marginal <math>Cm_1</math>, est exprimée par <math>Rm_1 = p + \frac{\partial p}{\partial Q}q_1 = \frac{\partial CT}{\partial q_1}Cm_1</math>. Cette équation montre que le coût marginal de l'entreprise 1 doit être égal au prix plus la variation du prix multipliée par la quantité produite par l'entreprise 1. | |||
De même, pour l'entreprise 2, la maximisation du profit est exprimée par <math>max_{q2} \pi_2 = p(Q)q_2 - CT(q_2)</math>, avec une condition de premier ordre similaire à celle de l'entreprise 1 : <math>Rm_2 = p + \frac{\partial p}{\partial Q}q_2 = \frac{\partial CT}{\partial q_2}Cm_2</math>. | |||
:<math>Q = | |||
L'aspect le plus crucial de ces équations est qu'elles illustrent l'interdépendance entre les entreprises dans un duopole. Les décisions de quantité de l'une affectent le prix de marché, qui à son tour affecte la recette marginale et donc les décisions de l'autre entreprise. En pratique, cela signifie que chaque entreprise doit anticiper la réaction de l'autre lorsqu'elle prend ses décisions de production. | |||
En résumé, dans un duopole, chaque entreprise doit tenir compte non seulement de ses propres coûts de production et de la demande du marché, mais aussi des actions de son concurrent. L'équilibre du marché est atteint lorsque les deux entreprises ont ajusté leur production de manière à ce que leurs recettes marginales soient égales à leurs coûts marginaux, prenant en compte les effets de leurs propres actions sur le prix du marché et donc sur les recettes marginales de l'autre. Cela conduit à un équilibre de Cournot dans lequel chaque entreprise produit une quantité telle que sa recette marginale est égale à son coût marginal, en tenant compte de la production de l'autre entreprise. | |||
== Équilibre de l'oligopole == | |||
Dans un oligopole où les entreprises agissent individuellement et sans coopération pour déterminer leur niveau de production, les résultats sont typiquement intermédiaires entre ceux d'un monopole et d'une concurrence parfaite. | |||
La quantité totale produite dans un oligopole est généralement plus importante que celle produite sous un monopole mais reste inférieure à la quantité qui serait produite dans un marché en concurrence parfaite. Ceci est dû à l'effet de l'interdépendance entre les firmes oligopolistiques : chaque firme, en maximisant son profit, ne prend pas en compte l'impact de sa production sur les bénéfices des autres firmes, à l'inverse d'un monopole qui contrôle l'ensemble de la production du marché. | |||
Le prix établi par les firmes en oligopole tend à être inférieur au prix de monopole, car la présence de concurrents sur le marché pousse les prix vers le bas. Cependant, ce prix reste supérieur au prix qui prévaudrait sous une concurrence parfaite. En concurrence parfaite, le prix du marché correspondrait au coût marginal (Cm), car les entreprises sont des preneuses de prix et ne peuvent fixer leurs prix au-dessus du coût marginal sans perdre toute leur clientèle. | |||
Les profits réalisés par les entreprises en oligopole sont également intermédiaires. Ils sont plus élevés que ce qu'ils seraient dans un marché en concurrence parfaite, où les profits économiques tendent vers zéro à long terme, mais ils sont inférieurs à ceux qu'une entreprise monopolistique pourrait réaliser. Cela s'explique par le fait qu'en concurrence parfaite, les entreprises ne peuvent pas fixer de prix au-dessus du coût marginal en raison de la présence de nombreux concurrents, tandis qu'en oligopole, le nombre réduit de concurrents confère un certain pouvoir de marché, permettant aux entreprises de maintenir les prix à un niveau supérieur au coût marginal et de réaliser ainsi un mark-up positif. | |||
En résumé, l'équilibre de l'oligopole se caractérise par un niveau de production, de prix et de profits qui reflètent le pouvoir de marché détenu par les entreprises oligopolistiques. Ce pouvoir de marché leur permet de fixer les prix au-dessus du coût marginal, réalisant ainsi un profit supérieur à celui d'un environnement de concurrence parfaite, mais sans atteindre les niveaux de profit qu'un monopole pourrait obtenir. | |||
== L'effet de la taille == | == L'effet de la taille == | ||
L'augmentation du nombre de vendeurs | L'augmentation du nombre de vendeurs dans un marché oligopolistique a tendance à pousser le marché vers des résultats similaires à ceux d'une concurrence parfaite. Cet effet peut être analysé à travers deux mécanismes principaux : l'effet quantité et l'effet prix. | ||
L'effet quantité est lié au fait que, dans un marché oligopolistique, le prix est généralement fixé au-dessus du coût marginal. Cela signifie que chaque unité supplémentaire vendue au prix courant va augmenter les profits, car le revenu généré par la vente de l'unité supplémentaire est supérieur au coût de sa production. Si le nombre de vendeurs augmente, la quantité totale offerte sur le marché va augmenter, ce qui devrait logiquement augmenter les profits globaux, toutes choses étant égales par ailleurs. | |||
L’effet prix concerne la baisse du prix qui résulte de l'augmentation de l'offre totale sur le marché. En effet, l'augmentation de la production totale peut saturer le marché et entraîner une baisse du prix en raison de la concurrence accrue entre les vendeurs. Cette baisse de prix va réduire le profit réalisé sur chaque unité vendue. | |||
Lorsque le nombre de vendeurs augmente, ces deux effets s'opposent. L'effet quantité cherche à augmenter les profits en vendant plus d'unités, tandis que l'effet prix tend à les diminuer en réduisant les revenus par unité. L'effet net sur les profits dépendra de la sensibilité de la demande aux changements de prix (l'élasticité de la demande) et de la capacité de production supplémentaire à influencer le marché. | |||
À mesure que le nombre de vendeurs augmente, l'effet prix devient de plus en plus dominant. Les prix commencent à baisser, se rapprochant du coût marginal. Cela diminue le pouvoir de marché de chaque vendeur et réduit les profits par unité. En théorie, si le nombre de vendeurs continue d'augmenter indéfiniment, le marché deviendrait parfaitement concurrentiel, le prix convergerait vers le coût marginal, et la quantité produite se rapprocherait du niveau socialement efficace, c'est-à-dire là où le prix égale le coût marginal. | |||
Dans un marché socialement efficace, les ressources sont allouées de la manière la plus avantageuse possible, maximisant le bien-être total des consommateurs et des producteurs. L'augmentation du nombre de vendeurs dans un marché oligopolistique peut donc mener à une allocation des ressources plus efficace, à des prix plus bas pour les consommateurs et à une augmentation de la quantité vendue, ce qui est bénéfique pour la société dans son ensemble. | |||
= La théorie des jeux et l'économie de la coopération = | = La théorie des jeux et l'économie de la coopération = | ||
La théorie des jeux est | == Eléments de théorie des jeux == | ||
La théorie des jeux est une branche mathématique et économique qui modélise et analyse comment les agents économiques prennent des décisions stratégiques dans des situations où les résultats dépendent non seulement de leurs propres décisions, mais aussi de celles des autres agents. Elle trouve des applications dans divers domaines tels que l'économie, la politique, la psychologie, la biologie et même dans les relations internationales. | |||
Dans le contexte de la théorie des jeux, une stratégie est un plan d'action complet qui spécifie le comportement à adopter dans toutes les situations possibles qui pourraient survenir. Cela pourrait impliquer une stratégie pure, où un joueur choisit une seule action spécifique, ou une stratégie mixte, où un joueur rend ses actions aléatoires en utilisant une distribution de probabilités sur plusieurs actions possibles. | |||
Les jeux peuvent être catégorisés comme statiques ou dynamiques. Dans un jeu statique, tous les joueurs choisissent leurs actions simultanément, ou du moins sans connaître les actions des autres. Les jeux dynamiques, quant à eux, se déroulent sur plusieurs périodes avec des actions à des moments différents, ce qui permet aux joueurs d'observer certaines des actions précédentes des autres joueurs avant de décider de leur propre stratégie. Cela peut introduire des considérations de réputation et de punition pour non-coopération, comme dans le dilemme des prisonniers répété. | |||
L'incertitude joue également un rôle clé dans la théorie des jeux. Dans beaucoup de jeux, les joueurs n'ont pas une information parfaite concernant les stratégies ou les types des autres joueurs. Cela mène à des stratégies où les joueurs doivent maximiser leurs gains attendus en tenant compte des probabilités des différentes actions des autres joueurs. | |||
La notion de stratégies crédibles est essentielle dans les jeux dynamiques. Une stratégie est dite crédible si un joueur a des incitations à s'y tenir même après que les étapes initiales du jeu se soient déroulées. Cela est souvent lié au concept d'engagement et aux menaces ou promesses dans des jeux séquentiels. | |||
La théorie des jeux utilise des outils mathématiques avancés pour résoudre des jeux et trouver des équilibres stratégiques, comme l'équilibre de Nash, où aucun joueur ne peut augmenter son gain attendu en changeant unilatéralement sa stratégie, en supposant que les autres joueurs maintiennent leurs stratégies constantes. La théorie des jeux aide à comprendre les comportements complexes en situation d'interdépendance et elle est fondamentale pour analyser les marchés économiques, en particulier les oligopoles, où les entreprises doivent constamment anticiper et réagir aux stratégies de leurs concurrents. | |||
== | == Théorie des jeux et oligopole == | ||
L'oligopole est un terrain classique pour l'application de la théorie des jeux en raison du nombre limité de firmes et de l'interdépendance de leurs décisions. Dans un tel marché, chaque entreprise doit prendre en compte les réactions potentielles de ses concurrents lorsqu'elle prend ses propres décisions de production et de tarification. | |||
Chaque entreprise, ou "joueur" dans le langage de la théorie des jeux, cherche à maximiser son profit. Cependant, contrairement à un marché en concurrence parfaite où chaque entreprise est une preneuse de prix et où son action individuelle n'a pas d'impact sur le marché, ou à un monopole où l'entreprise a un contrôle total sur le marché, chaque firme en oligopole sait que ses actions influenceront et seront influencées par les actions de ses concurrents. C'est un exemple de jeu à somme non nulle, où les profits de l'une ne sont pas forcément les pertes des autres, et les stratégies optimales dépendent fortement des choix des autres joueurs. | |||
Dans un marché oligopolistique, les entreprises peuvent opérer sous une information complète mais imparfaite. Information complète signifie que toutes les entreprises connaissent toutes les stratégies possibles et les payoffs associés à chaque combinaison de stratégies pour tous les joueurs. Cependant, l'information est imparfaite car, bien que chaque entreprise connaisse les payoffs et les stratégies, elle ne connaît pas les choix de stratégie que les autres entreprises feront ou ont fait. | |||
La simultanéité des actions ajoute à la complexité stratégique. Chaque entreprise doit choisir son niveau de production et son prix sans savoir précisément ce que les autres vont faire. Cela peut conduire à des résultats variés, y compris des équilibres précaires qui peuvent être perturbés par des changements dans les stratégies des entreprises ou des entrées de nouvelles firmes sur le marché. | |||
Le concept d'équilibre de Nash est particulièrement pertinent ici : c'est une situation où, connaissant les stratégies des autres, aucune entreprise n'a intérêt à changer unilatéralement sa propre stratégie. Cet équilibre reflète une sorte de trêve stratégique où chaque entreprise, en supposant que les autres ne changent pas leur stratégie, choisit la meilleure réponse à ces stratégies. | |||
En pratique, cela peut mener à des stratégies qui incluent des compromis entre agressivité et prudence, l'adoption de stratégies de signalisation, ou des tentatives de coopération tacite pour éviter des guerres de prix destructrices. La théorie des jeux fournit donc un cadre pour comprendre et prédire les comportements dans ces marchés complexes. | |||
== L'équilibre de Nash == | |||
John F. Nash a apporté une contribution fondamentale à la théorie des jeux avec sa caractérisation de l'équilibre pour les jeux non coopératifs. Cet équilibre, connu sous le nom d'équilibre de Nash, est devenu un concept central de la théorie des jeux moderne et a des applications dans de nombreux domaines allant de l'économie à la biologie et au-delà. | |||
L'équilibre de Nash est une situation où aucun joueur n'a intérêt à changer de stratégie tant que les autres joueurs maintiennent les leurs. Cela signifie que, même si les joueurs ne coopèrent pas ou ne communiquent pas entre eux, ils arrivent à un état où les stratégies sont mutuellement les meilleures réponses les unes aux autres. Chaque joueur, en regardant ce que font les autres, choisit la meilleure stratégie possible pour lui-même. | |||
Il est crucial de noter que l'équilibre de Nash ne correspond pas nécessairement à l'optimalité du point de vue du groupe ou du bien-être social. Dans certains jeux, comme le célèbre dilemme du prisonnier, l'équilibre de Nash peut conduire à un résultat sous-optimal pour tous les participants. Cela est dû au fait que l'équilibre de Nash reflète ce qui est meilleur pour chaque individu dans le contexte des choix des autres, mais pas nécessairement ce qui est optimal pour l'ensemble des joueurs. | |||
Quand un joueur a une stratégie dominante, elle lui donnera le meilleur résultat peu importe ce que les autres joueurs décident de faire. Si tous les joueurs ont une stratégie dominante, l'équilibre de Nash est simple à trouver : chaque joueur choisira sa stratégie dominante. Cependant, dans de nombreux jeux plus complexes, les joueurs n'ont pas de stratégies dominantes et doivent tenir compte de manière plus nuancée des stratégies potentielles des autres joueurs pour déterminer leur meilleure réponse. | |||
L'équilibre de Nash a été une avancée importante car il fournit un moyen de prédire les résultats dans des situations où les individus prennent des décisions qui sont interdépendantes, ce qui est un aspect commun à de nombreuses situations économiques, sociales et biologiques. La reconnaissance de l'importance de ce concept par le Comité Nobel souligne son influence étendue et sa pertinence pour les sciences sociales. | |||
== Le dilemme du prisonnier == | |||
Le dilemme du prisonnier est un exemple classique en théorie des jeux qui démontre le conflit entre les intérêts individuels et le bien-être collectif. C'est un jeu non coopératif où, malgré l'existence d'un résultat coopératif qui serait meilleur pour les deux parties, l'équilibre de Nash prédit un résultat non coopératif où chaque joueur opte pour sa stratégie dominante, conduisant à un résultat sous-optimal pour les deux. | |||
Le jeu se déroule habituellement comme suit : deux criminels présumés sont arrêtés et interrogés séparément. Chacun a la possibilité de trahir l'autre en avouant, ou de coopérer avec l'autre en restant silencieux. Si l'un trahit et l'autre reste silencieux, le traître est libéré tandis que l'autre reçoit la peine maximale. Si tous deux trahissent, ils reçoivent tous les deux une peine sévère, mais moins que la peine maximale. Si tous deux restent silencieux, ils reçoivent tous les deux une peine plus légère. | |||
Le dilemme réside dans le fait que, bien que la coopération (tous les deux restent silencieux) conduirait à un meilleur résultat global, la stratégie dominante pour chaque joueur est de trahir l'autre. En effet, peu importe ce que fait l'autre joueur, chaque joueur a une meilleure issue en trahissant : soit il est libéré (si l'autre coopère), soit il reçoit une peine moins lourde (si l'autre trahit également). Par conséquent, l'équilibre de Nash est que les deux joueurs trahissent, résultant en une peine plus lourde pour les deux, ce qui est un résultat pire que si les deux avaient coopéré. | |||
Dans | Dans le contexte des marchés oligopolistiques, le dilemme du prisonnier illustre pourquoi les firmes ont du mal à maintenir la coopération, comme dans le cas d'un cartel où les firmes pourraient bénéficier de profits plus élevés en limitant la production pour maintenir les prix élevés. Malgré ces avantages potentiels, la tentation de trahir le cartel en produisant plus pour augmenter sa propre part de marché rend la coopération instable. Chaque firme sait que si elle ne trahit pas et que l'autre le fait, elle se retrouvera avec le pire résultat possible. Ainsi, le manque de confiance et l'incitation à agir dans son propre intérêt poussent les firmes vers la non-coopération, souvent au détriment du bien-être collectif. | ||
Le dilemme du prisonnier est un exemple emblématique de la théorie des jeux qui montre comment les intérêts individuels peuvent entrer en conflit avec l'intérêt collectif, même quand la coopération serait bénéfique pour tous les participants. | |||
Dans ce scénario, les deux prisonniers sont confrontés à un choix sans la possibilité de coordonner leurs actions. Le tableau des payoffs pour ce jeu peut être décrit comme suit : | |||
* Si aucun des deux prisonniers n'avoue (coopération mutuelle), ils écopent tous les deux d'une peine mineure d'un an. | |||
* Si l'un avoue (trahit) et l'autre non, le traître est relâché tandis que celui qui reste silencieux est sévèrement puni avec vingt ans de prison. | |||
* Si les deux avouent (défaut mutuel), ils reçoivent tous les deux une peine de huit ans de prison. | |||
La difficulté vient du fait que chaque prisonnier doit prendre une décision sans savoir ce que l'autre va faire. La stratégie dominante (la meilleure action à prendre quelle que soit l'action de l'autre joueur) pour chacun est d'avouer, car cela maximise l'utilité individuelle quel que soit le choix de l'autre prisonnier. Ainsi, l'équilibre de Nash dans ce jeu est pour les deux prisonniers d'avouer, car en faisant ce choix, aucun des deux ne peut améliorer sa situation en changeant unilatéralement sa décision. | |||
Cependant, l'équilibre de Nash n'est pas l'optimum de Pareto dans ce cas. L'optimum de Pareto est une situation où il n'est pas possible d'améliorer la situation de quelqu'un sans détériorer celle d'un autre. Si les deux prisonniers pouvaient s'entendre pour ne pas avouer, ils seraient tous les deux mieux lotis avec seulement un an de prison chacun. Mais, en raison de l'impossibilité de communiquer et de l'incertitude concernant les actions de l'autre, ils finissent par choisir une stratégie qui les conduit à un résultat mutuellement défavorable. | |||
Le | Le dilemme du prisonnier illustre bien le défi de la coopération dans de nombreuses situations économiques, politiques et sociales, où la confiance et la communication sont essentielles pour atteindre des résultats mutuellement avantageux. Il démontre également la complexité des interactions humaines et la difficulté de prendre des décisions rationnelles dans des situations d'incertitude. | ||
[[Fichier:Oligopole dilemme du prisonnier 1.png|400px|vignette|centré|Equilibre de Nash unique: (Avoue, Avoue). Equilibre non-optimal: les deux joueurs pourraient améliorer leur situation en se taisant. La coopération est difficile à maintenir car elle n’est pas un choix rationnel au niveau individuel. NB: ici, le jeu est symétrique, mais ce n’est pas nécessairement le cas.]] | |||
La matrice des payoffs fournie représente les résultats possibles du dilemme du prisonnier pour deux suspects, "Brute" et "Truand". Chaque suspect a deux options : avouer ou se taire. Les payoffs sont exprimés en termes d'années de prison que chaque suspect encourt en fonction de la décision prise, à la fois par lui-même et par l'autre. | |||
Analysons les payoffs : | |||
* Si les deux avouent, chacun reçoit une peine de 8 ans de prison. | |||
* Si Brute avoue mais que Truand se tait, Brute est libéré et Truand reçoit la peine maximale de 20 ans de prison. | |||
* Si Brute se tait mais que Truand avoue, Brute reçoit la peine maximale de 20 ans de prison et Truand est libéré. | |||
* Si les deux se taisent, chacun reçoit une peine mineure d'1 an de prison. | |||
Le dilemme se situe dans le fait que bien que le meilleur résultat collectif soit atteint lorsque les deux se taisent (1 an de prison chacun), la décision rationnelle pour chaque individu, lorsque l'on considère les actions de l'autre comme données, est d'avouer. Ainsi, si Truand pense que Brute va se taire, il devrait avouer pour être libéré. De même, si Truand pense que Brute va avouer, il devrait aussi avouer pour éviter la peine de 20 ans. La même logique s'applique à Brute. Par conséquent, l'équilibre de Nash de ce jeu est que les deux avouent, puisque avouer est la meilleure réponse pour chaque suspect quel que soit le choix de l'autre. | |||
Cet équilibre de Nash est unique et il est non-optimal car il mène à un résultat où les deux joueurs obtiennent un payoff pire que s'ils avaient choisi de se taire. Cela illustre la difficulté de maintenir la coopération, car bien que coopérer soit mutuellement avantageux, elle n'est pas un choix rationnel au niveau individuel sans une communication et une confiance entre les joueurs. | |||
La symétrie de ce jeu signifie que les payoffs sont identiques pour les stratégies miroirs des deux joueurs. Cependant, la théorie des jeux s'applique également à des jeux non symétriques où les stratégies et les payoffs peuvent varier d'un joueur à l'autre, ce qui peut complexifier davantage l'analyse et la détermination des équilibres. | |||
== Un jeu de course à l'armement == | |||
Un jeu de course à l'armement est un exemple classique de dilemme de sécurité qui se produit souvent dans les relations internationales et peut être analysé à l'aide de la théorie des jeux. Dans ce scénario, deux pays (ou plus) doivent décider s'ils doivent augmenter leur arsenal militaire. Bien que chaque pays puisse bénéficier individuellement d'une position plus forte en s'armant davantage, si tous les pays choisissent de s'armer, cela pourrait conduire à une augmentation des tensions, à une instabilité régionale et, dans le pire des cas, à un conflit armé. | |||
Voici comment un jeu de course à l'armement pourrait être structuré en termes de théorie des jeux : | |||
* Les Joueurs : Deux pays, Pays A et Pays B. | |||
* Les Stratégies : Chaque pays a deux options - s'armer ou ne pas s'armer. | |||
* Les Payoffs : Les gains sont déterminés non seulement par la décision d'un pays de s'armer ou non, mais aussi par la décision prise par l'autre pays. | |||
Les résultats possibles sont les suivants : | |||
* Désarmement Mutuel : Si les deux pays choisissent de ne pas s'armer, ils évitent les coûts liés à une course aux armements et peuvent bénéficier d'une plus grande stabilité et de relations pacifiques. Cependant, ils peuvent se sentir vulnérables à des menaces extérieures. | |||
* Course aux Armements : Si les deux pays choisissent de s'armer, cela augmente les dépenses militaires et la tension, réduisant potentiellement la sécurité globale. | |||
* Déséquilibre : Si un pays s'arme et que l'autre ne le fait pas, le pays armé pourrait se sentir plus en sécurité avec un avantage militaire, tandis que le pays désarmé pourrait se sentir vulnérable et désavantagé. | |||
* Stabilité de Nash : L'équilibre de Nash dans ce jeu est souvent la situation où les deux pays s'arment, car chaque pays a la stratégie dominante de s'armer pour garantir sa sécurité quelles que soient les actions de l'autre. | |||
L'ironie de la course à l'armement est que, bien que chaque pays cherche à augmenter sa propre sécurité en s'armant, l'armement mutuel peut en fait réduire la sécurité globale, un concept connu sous le nom de paradoxe de la sécurité. Ce paradoxe est semblable au dilemme du prisonnier en ce que les résultats individuellement rationnels conduisent à un résultat collectivement irrationnel ou sous-optimal. | |||
Dans la réalité, ces jeux sont souvent répétés ou dynamiques, avec une histoire de mouvements précédents qui peuvent influencer les stratégies actuelles. En outre, les éléments tels que les alliances, les traités et les organismes internationaux peuvent jouer un rôle dans la modification des payoffs et des choix stratégiques disponibles pour les pays. | |||
[[Fichier:Oligopole dilemme du prisonnier 2.png|400px|vignette|centré|Stratégie dominante dans le jeu du dilemme du prisonnier: "avoue" ici: "s'armer".]] | |||
L'image montre une matrice de payoff pour un jeu de course à l'armement entre deux superpuissances historiques, l'URSS et les États-Unis. La matrice représente les conséquences de deux stratégies disponibles pour chacun des acteurs : "s'armer" ou "se désarmer". Les résultats sont basés sur la combinaison des choix des deux pays. | |||
Analysons les payoffs dans chaque scénario : | |||
* Si l'URSS et les États-Unis choisissent tous les deux de "s'armer", ils sont tous deux "soumis au risque", ce qui implique une augmentation des tensions et une sécurité réduite en raison de la probabilité accrue de confrontation militaire. | |||
* Si l'URSS décide de "s'armer" tandis que les États-Unis choisissent de "se désarmer", l'URSS est "en sécurité et puissante" tandis que les États-Unis sont "soumis au risque et affaiblis". Cela donne un avantage stratégique à l'URSS, laissant les États-Unis vulnérables. | |||
* Si l'URSS choisit de "se désarmer" tandis que les États-Unis décident de "s'armer", les rôles sont inversés avec les États-Unis en position de sécurité et de puissance, et l'URSS soumise au risque et affaiblie. | |||
* Si les deux décident de "se désarmer", ils sont tous les deux "en sécurité", ce qui serait l'issue la plus pacifique et la plus stable, réduisant le risque d'un conflit armé. | |||
La | La stratégie dominante pour les deux joueurs dans ce jeu, similaire à la stratégie "avoue" dans le dilemme du prisonnier classique, est de "s'armer". Indépendamment de la décision prise par l'autre partie, chaque pays a un meilleur résultat (en termes de sécurité et de pouvoir) lorsqu'il choisit de s'armer. Par conséquent, l'équilibre de Nash de ce jeu est que les deux pays finissent par s'armer, car aucune des parties n'a un incitatif unilatéral à se désarmer. Cependant, tout comme dans le dilemme du prisonnier, cet équilibre n'est pas socialement optimal ; les deux pays seraient mieux si tous les deux choisissaient de se désarmer, réduisant ainsi les risques de conflit tout en économisant des ressources dépensées dans l'armement. | ||
Cet exemple illustre clairement le paradoxe de la sécurité : en cherchant à augmenter leur sécurité par des moyens militaires, les pays peuvent en fait diminuer leur sécurité globale en raison de la réaction réciproque et de la méfiance qu'elle génère. Cela démontre la complexité de la coopération internationale et les défis associés à la prise de décisions dans un environnement international souvent incertain et basé sur la perception des actions des autres. | |||
== Le duopole comme dilemme du prisonnier == | == Le duopole comme dilemme du prisonnier == | ||
Le duopole peut être conceptualisé comme un dilemme du prisonnier, où deux entreprises (ou duopolistes) sont confrontées à la décision de coopérer pour maximiser leurs profits collectifs ou de concurrencer agressivement pour maximiser leurs profits individuels. Si les deux entreprises coopèrent, elles peuvent agir de concert pour fixer des prix élevés et limiter leur production, se comportant essentiellement comme un monopole et se partageant les profits maximaux possibles. Cependant, la tentation d'augmenter la part de marché individuelle en produisant plus et en vendant à un prix inférieur peut mener à un résultat non coopératif, qui est moins avantageux pour les deux. | |||
Dans la structure d'un duopole, chaque entreprise doit prendre en compte les actions potentielles de son concurrent lorsqu'elle prend ses décisions stratégiques. La théorie des jeux prédit que si chaque entreprise poursuit son intérêt individuel sans accord contraignant de coopération, elles finiront toutes les deux par produire plus, baisser les prix, et voir leurs profits diminuer par rapport à ce qu'ils auraient été sous coopération. Cela est dû au fait que chaque entreprise vise à maximiser son propre profit sans tenir compte de l'impact de ses actions sur le profit global du marché, ce qui peut conduire à une surproduction et à une diminution des prix. | |||
L'équilibre de Nash dans un tel duopole est similaire au dilemme du prisonnier, où chaque entreprise choisit de ne pas coopérer (c'est-à-dire produire plus et baisser les prix) car cette stratégie maximise son profit étant donné la stratégie de l'autre entreprise. C'est l'équilibre stable car si une entreprise dévie et réduit sa production dans l'espoir d'augmenter les prix, elle risque de perdre des parts de marché si l'autre entreprise ne suit pas. Ainsi, même si les deux entreprises seraient mieux loties en coopérant, la nature non contraignante de leur interaction et le manque de communication et de confiance mutuelle les mènent à un équilibre non coopératif. | |||
Cependant, il est important de noter que dans le monde réel, les entreprises en oligopole peuvent trouver des moyens de surmonter ce dilemme par divers moyens, tels que la formation de cartels, l'établissement de règles de concurrence tacites ou l'adoption de stratégies de différenciation de produits, qui peuvent les aider à maintenir des prix élevés et à se rapprocher de la profitabilité du monopole. Ces méthodes, cependant, peuvent être limitées par des lois antitrust et d'autres régulations visant à maintenir la concurrence sur les marchés. | |||
[[Fichier:Oligopole dilemme du prisonnier 3.png|400px|vignette|centré]] | |||
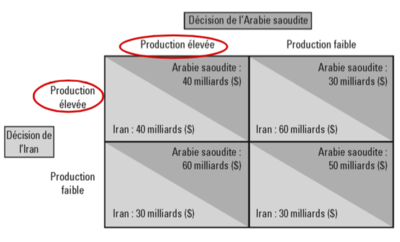
L'image représente une matrice de payoff qui illustre un jeu de duopole entre l'Iran et l'Arabie saoudite, centré sur leur décision de production pétrolière. Chaque pays a la possibilité de choisir entre une production élevée ou faible. Les payoffs sont exprimés en milliards de dollars, reflétant probablement le profit ou le revenu que chaque pays s'attend à gagner en fonction de la combinaison de leurs décisions de production. | |||
Lorsque les deux pays choisissent une production élevée, l'Arabie saoudite et l'Iran gagnent chacun 40 milliards de dollars. Cette situation peut être interprétée comme une surproduction qui entraîne une baisse des prix du pétrole sur le marché mondial, réduisant ainsi les revenus pour les deux producteurs. | |||
Si l'Iran augmente sa production tandis que l'Arabie saoudite réduit la sienne, l'Iran gagne plus (60 milliards de dollars) tandis que l'Arabie saoudite voit ses revenus diminuer à 30 milliards de dollars. L'inverse est également vrai : si l'Iran réduit sa production et que l'Arabie saoudite augmente la sienne, l'Iran obtient 30 milliards de dollars et l'Arabie saoudite 60 milliards de dollars. | |||
Dans le cas où les deux pays décident de réduire leur production, l'Arabie saoudite gagne 50 milliards de dollars et l'Iran 30 milliards de dollars. Cela peut refléter des prix plus élevés en raison d'une offre réduite, mais avec une part de marché plus grande pour l'Arabie saoudite, expliquant pourquoi ses revenus sont plus élevés que ceux de l'Iran. | |||
L'équilibre de Nash dans ce jeu, en supposant que chaque joueur agit rationnellement et en connaissant les stratégies de l'autre, serait pour les deux pays de choisir une production élevée. C'est parce que, quelle que soit la décision de l'autre pays, chaque pays a un meilleur payoff en choisissant une production élevée (passant de 30 à 40 milliards si l'autre se désarme, et de 50 à 60 milliards si l'autre augmente également sa production). | |||
Cependant, cet équilibre de Nash n'est pas l'optimum de Pareto. Les deux pays seraient collectivement mieux lotis si tous deux choisissaient de limiter leur production, car ils pourraient potentiellement augmenter leurs profits globaux grâce à des prix plus élevés pour leur pétrole. Cependant, sans un accord de coopération qui serait contraignant pour les deux parties, l'intérêt individuel incite chaque pays à augmenter sa production, menant à un équilibre moins avantageux pour tous les deux, similaire à la dynamique observée dans le dilemme du prisonnier. | |||
== Un jeu de publicité == | == Un jeu de publicité == | ||
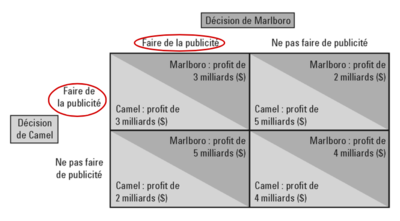
Cette matrice de payoff décrit un jeu de stratégie de publicité entre deux entreprises concurrentes, Camel et Marlboro. Chacune de ces entreprises doit décider si elle doit faire de la publicité ou non. Les profits résultants pour chaque entreprise dépendent de leur choix de stratégie combiné avec le choix de l'autre entreprise. | |||
[[Fichier:Oligopole un jeu de publicité 1.png|400px|vignette|centré]] | |||
Les profits sont les suivants selon les décisions prises par Camel et Marlboro : | |||
* Si Camel et Marlboro choisissent tous deux de faire de la publicité, ils gagnent chacun 3 milliards de dollars. Cela pourrait signifier que les coûts de la publicité érodent une partie des profits additionnels qu'ils pourraient obtenir grâce à l'augmentation des ventes. | |||
* Si Camel fait de la publicité tandis que Marlboro ne le fait pas, Camel gagne 5 milliards de dollars et Marlboro seulement 2 milliards de dollars. Cela suggère que Camel tire un avantage significatif de la publicité en capturant une part de marché plus importante, tandis que Marlboro souffre d'une baisse de visibilité et de ventes. | |||
* Si Camel choisit de ne pas faire de publicité mais que Marlboro fait de la publicité, Camel gagne 2 milliards de dollars et Marlboro 5 milliards de dollars. Dans ce cas, Marlboro bénéficie de l'avantage de la publicité. | |||
* Si ni Camel ni Marlboro ne font de la publicité, Camel gagne 4 milliards de dollars et Marlboro 4 milliards de dollars également. Cela peut refléter une situation où les deux entreprises bénéficient de coûts inférieurs en n'engageant pas de dépenses publicitaires, tout en maintenant une certaine parité dans la part de marché. | |||
L'analyse de cette matrice de payoff montre que la publicité est une stratégie dominante pour les deux entreprises. Peu importe ce que fait l'autre entreprise, chaque entreprise a un meilleur profit en faisant de la publicité. Par conséquent, l'équilibre de Nash dans ce jeu est pour les deux entreprises de choisir de faire de la publicité, car c'est la meilleure stratégie pour chacune d'elles indépendamment de la stratégie de l'autre. | |||
Cependant, ce n'est pas l'optimum de Pareto car les deux entreprises pourraient potentiellement gagner plus (4 milliards chacune) si aucune des deux ne faisait de publicité. Cet exemple illustre comment, même si une certaine stratégie (comme ne pas faire de publicité) pourrait être meilleure collectivement, les incitations individuelles à agir autrement conduisent à un résultat sous-optimal. Cela reflète la nature compétitive de la publicité où les entreprises sont souvent contraintes d'engager des dépenses importantes pour rester pertinentes et compétitives, même si cela réduit leurs profits globaux. | |||
== Un jeu de ressources communes == | == Un jeu de ressources communes == | ||
L'image ci-dessous représente une matrice de payoff pour un jeu de ressources communes entre deux compagnies pétrolières, BP et Shell. Chaque compagnie doit décider entre creuser un ou deux puits pétroliers. Les profits résultant de chaque combinaison de décisions sont exprimés en millions d'euros. | |||
[[Fichier:Oligopole Un jeu de ressources communes.png|400px|vignette|centré]] | |||
Si BP et Shell décident tous les deux de creuser deux puits, ils gagnent chacun 4 millions d'euros. Cette situation peut refléter une sur-exploitation de la ressource partagée, où l'augmentation de la production entraîne une baisse des prix du pétrole ou une épuisement plus rapide de la ressource, ce qui réduit les profits pour les deux compagnies. | |||
Lorsque BP choisit de creuser deux puits tandis que Shell n'en creuse qu'un, BP gagne moins (3 millions d'euros) par rapport à Shell qui en gagne 6. Cette asymétrie peut survenir parce que Shell, en limitant sa production, bénéficie de prix plus élevés ou conserve ses ressources pour l'avenir, tandis que BP, en augmentant sa production, pourrait subir une baisse des prix due à une offre excédentaire. | |||
Inversement, si BP décide de creuser un seul puits et que Shell en creuse deux, BP gagne 5 millions d'euros et Shell seulement 6 millions d'euros. Dans ce cas, Shell ne tire pas un avantage proportionnel à son investissement accru par rapport à BP, ce qui peut refléter une saturation du marché ou des coûts d'extraction croissants. | |||
Si les deux compagnies choisissent de creuser un seul puits, Shell gagne 5 millions d'euros et BP gagne 6 millions d'euros. Cette situation peut indiquer que la modération dans l'exploitation des ressources conduit à de meilleurs prix du pétrole ou à une gestion plus durable des ressources, augmentant ainsi les profits. | |||
Dans | Dans ce jeu, il n'y a pas de stratégie dominante pour les deux joueurs. Le choix de la meilleure stratégie dépend de la décision de l'autre compagnie. Si BP suppose que Shell va creuser deux puits, BP maximise ses profits en creusant seulement un puits. Si BP pense que Shell va creuser un seul puit, BP aurait intérêt à creuser deux puits. La même logique s'applique à Shell. | ||
L'équilibre de Nash de ce jeu est moins évident. Si les deux compagnies raisonnent strictement selon les payoffs, elles pourraient finir par creuser un seul puit chacune, ce qui n'est pas le résultat le moins profitable pour aucune des deux parties. Cependant, si l'une des entreprises s'attend à ce que l'autre se modère, elle pourrait être tentée de creuser deux puits pour maximiser ses profits immédiats, ce qui pourrait conduire à une sur-exploitation. Cette situation reflète un "dilemme des communs", où les acteurs individuels profitent de la sur-utilisation d'une ressource partagée, ce qui peut mener à une épuisement à long terme de cette ressource au détriment de tous. | |||
== Le jeu oligopolistique UN et DEUX == | == Le jeu oligopolistique UN et DEUX == | ||
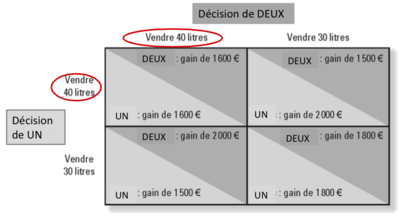
L'image ci-dessous représente une matrice de payoff pour un jeu oligopolistique entre deux producteurs, UN et DEUX, qui doivent décider de la quantité de produit à vendre, soit 30 litres ou 40 litres. Les gains associés à chaque décision dépendent de l'action prise par l'autre producteur. | |||
[[Fichier:Le jeu oligopolistique UN et DEUX1.png|400px|vignette|centré]] | |||
Si UN et DEUX choisissent tous deux de vendre 40 litres, ils gagnent chacun 1 600 euros. Cela peut indiquer une situation de concurrence où l'augmentation de l'offre a entraîné une baisse des prix, ce qui diminue les profits des deux producteurs. | |||
Lorsque UN choisit de vendre 40 litres tandis que DEUX vend 30 litres, UN gagne 1 600 euros et DEUX gagne 2 000 euros. Inversement, si UN vend 30 litres et DEUX vend 40 litres, UN gagne 2 000 euros tandis que DEUX gagne 1 500 euros. Ces scénarios montrent qu'un producteur peut bénéficier de gains plus élevés en vendant moins si son concurrent inonde le marché avec une quantité plus importante, probablement à cause d'une meilleure tarification due à une offre plus limitée. | |||
Si les deux producteurs décident de vendre 30 litres chacun, UN gagne 1 800 euros et DEUX gagne 1 800 euros également. Cette décision reflète probablement une entente tacite ou une coopération où les deux producteurs réduisent leur offre pour maintenir des prix plus élevés et maximiser leurs profits. | |||
L'équilibre de non-coopération, basé sur la matrice de payoff, est atteint lorsque les deux producteurs choisissent de vendre 40 litres, car vendre 40 litres est une stratégie dominante pour chacun d'eux. C'est le résultat naturel en l'absence de coopération, car chaque producteur réagit aux actions de l'autre en maximisant son propre profit sans considération pour le profit collectif. | |||
L'optimum pour les producteurs, qui maximiserait leur profit total, serait de coopérer et de choisir de vendre 30 litres chacun. Cela nécessiterait une certaine forme de communication ou d'accord pour limiter la production, ce qui pourrait ne pas être légal dans certains marchés réglementés en raison des lois antitrust et de concurrence. | |||
Ce jeu illustre le défi central des oligopoles : trouver un équilibre entre les incitations individuelles à augmenter la production pour maximiser les profits individuels et les avantages potentiels d'une action collective qui pourrait conduire à de meilleurs résultats pour tous les producteurs. Sans coopération, les producteurs se retrouvent dans un équilibre de Nash non coopératif, qui n'est pas l'optimum de Pareto car ils pourraient tous deux être mieux lotis s'ils limitaient leur production. Cet équilibre reflète également le dilemme du prisonnier, où les joueurs ne parviennent pas à atteindre un accord mutuellement avantageux en raison des incitations à agir de manière indépendante. | |||
== La coopération dans un cadre dynamique == | == La coopération dans un cadre dynamique == | ||
Dans un contexte dynamique où les jeux se répètent sur une longue période, la coopération entre les duopolistes peut devenir une stratégie plus stable et potentiellement plus profitable que la compétition agressive. Ce phénomène est souvent analysé dans le cadre des jeux répétés, aussi connus sous le nom de jeux itératifs ou supergames. | |||
Lorsque | Lorsque les firmes prennent en compte les profits futurs et non pas seulement les gains immédiats, elles peuvent reconnaître qu'une stratégie de coopération à long terme maximisera leurs profits globaux. Dans cette perspective, même si une entreprise peut obtenir un gain ponctuel en trichant et en rompant l'accord de coopération, elle pourrait perdre beaucoup plus en profits futurs si l'autre entreprise répond en revenant à un comportement non coopératif. | ||
UN | La menace d'une punition crédible joue un rôle clé dans la stabilité de la coopération. Si UN décide de tricher, DEUX peut "punir" UN en cessant la coopération et en revenant à la compétition, ce qui réduit les profits pour les deux firmes. Pour que cette punition soit crédible, DEUX doit être prête et capable de renoncer à ses gains à court terme pour maintenir la discipline à long terme. Si cette punition est crédible et si les entreprises anticipent correctement les conséquences à long terme de leurs actions, alors la coopération peut se maintenir. | ||
La répétition du jeu sans date de fin, ou | La répétition du jeu sans une date de fin connue ou dans un contexte d'incertitude quant à la durée de l'interaction peut renforcer la coopération. Si les entreprises ne savent pas quand le jeu se terminera, elles ont moins d'incitations à tricher, car elles ne peuvent pas être sûres que le gain à court terme vaudra le coût des profits perdus à l'avenir. | ||
La théorie des jeux répétés suggère que les stratégies de coopération peuvent être soutenues par le "shadow of the future" ou l'ombre du futur. Plus le futur influence les décisions présentes, plus il est probable que les entreprises adopteront des stratégies qui favorisent la coopération. Les entreprises peuvent donc développer des mécanismes de coopération tels que des accords tacites, des stratégies de réciprocité ou des contrats à long terme pour stabiliser cette coopération et maximiser leurs profits collectifs sur le long terme. | |||
= L'oligopole et le rôle de l'État = | = L'oligopole et le rôle de l'État = | ||
== L'oligopole et le rôle de l'État == | == L'oligopole et le rôle de l'État == | ||
Dans le contexte économique d'un oligopole, la coopération entre les entreprises pour fixer les prix ou limiter la production peut être bénéfique pour ces entreprises, car elle leur permet d'augmenter leurs profits en exerçant un pouvoir de marché similaire à celui d'un monopole. Cependant, cette coopération peut être préjudiciable aux consommateurs et à la société dans son ensemble, car elle peut entraîner des prix artificiellement élevés et une production inférieure à celle qui serait réalisée dans un marché plus concurrentiel. Cela peut conduire à une allocation inefficace des ressources, à une innovation moindre et à des choix réduits pour les consommateurs. | |||
Pour cette raison, de nombreux gouvernements ont mis en place des lois antitrust ou de la concurrence pour réguler les comportements des entreprises dans les marchés oligopolistiques. Ces lois visent à prévenir les pratiques anticoncurrentielles telles que les cartels, les ententes sur les prix, les pratiques monopolistiques et les abus de position dominante. Le but est de protéger les intérêts des consommateurs, de promouvoir l'innovation et d'assurer une concurrence équitable sur le marché. | |||
Cependant, l'approche réglementaire peut varier d'un pays à l'autre. Certains pays ont des lois antitrust très strictes et des organismes de réglementation actifs qui surveillent de près les marchés et sanctionnent les comportements anticoncurrentiels. D'autres pays peuvent avoir une approche plus souple, soit en raison de différences dans la philosophie économique, soit en raison de capacités de réglementation et de mise en œuvre plus faibles. | |||
Les économistes ne s'accordent pas toujours sur le degré et la forme de la régulation qui devraient être appliqués. Certains plaident pour des marchés plus libres, arguant que la réglementation peut être lourde et entraver l'efficacité du marché. D'autres soutiennent que sans réglementation, les consommateurs peuvent être exploités par des entreprises puissantes. Les économistes peuvent également être en désaccord sur les effets des oligopoles sur l'innovation - certains suggèrent que les profits élevés dans les oligopoles peuvent financer la recherche et le développement, tandis que d'autres pensent que la concurrence est un meilleur stimulant pour l'innovation. | |||
Le rôle de l'État dans la régulation des oligopoles est donc crucial et complexe. Il doit équilibrer la protection des consommateurs et la promotion de la concurrence avec la reconnaissance des réalités économiques des industries où les économies d'échelle ou les exigences de capital rendent le nombre d'acteurs naturellement limité. Cela implique souvent un ajustement constant des politiques et des réglementations pour s'adapter aux changements du marché et aux nouvelles informations. | |||
== États-Unis : le Sherman Antitrust Act == | == États-Unis : le Sherman Antitrust Act == | ||
Standard Oil de | Le Sherman Antitrust Act est une législation fondamentale aux États-Unis qui a établi les bases de la réglementation antitrust moderne. Adoptée en 1890, cette loi visait à lutter contre les pratiques anticoncurrentielles et à démanteler les monopoles, ce qui était un problème croissant à l'époque de l'ère industrielle, notamment avec l'ascension de compagnies comme la Standard Oil de John D. Rockefeller. | ||
Le Sherman Act est particulièrement remarquable pour deux de ses dispositions principales : | |||
* Section 1 : Cette section interdit les accords anticoncurrentiels entre entreprises, y compris les cartels, les ententes sur les prix et d'autres formes de collusion qui restreignent le commerce. | |||
* Section 2 : Elle cible les comportements monopolistiques, interdisant les situations où une entreprise monopolise ou tente de monopoliser un marché. | |||
Le passage cité indique clairement que toute forme d'accord ou de complot visant à restreindre le commerce est illégal et que les individus ou entreprises coupables de tels actes seront considérés comme des criminels, passibles de lourdes amendes et/ou de peines de prison. | |||
Le Clayton Act, qui a été adopté en 1914, a complété le Sherman Act en abordant des questions plus spécifiques et en ciblant certaines pratiques qui n'étaient pas explicitement interdites par le Sherman Act. Par exemple, le Clayton Act a mis l'accent sur des problèmes tels que la discrimination par les prix, les accords d'exclusivité et les acquisitions d'actions qui pourraient réduire la concurrence. | |||
Ces lois sont des éléments clés de la politique de concurrence américaine et continuent d'influencer la manière dont les affaires sont menées non seulement aux États-Unis mais aussi dans les interactions commerciales internationales. L'application de ces lois est assurée par le Department of Justice des États-Unis ainsi que par la Federal Trade Commission (FTC), qui ont le pouvoir de poursuivre les entreprises pour pratiques anticoncurrentielles et de demander aux tribunaux de prendre des mesures telles que la dissolution de trusts, l'imposition d'amendes ou l'interdiction de certaines transactions commerciales. Ces lois ont joué un rôle déterminant dans la préservation de la concurrence sur les marchés américains et sont considérées comme un modèle pour les réglementations antitrust dans d'autres juridictions. | |||
== Europe : le Traité de Rome (art. 82) == | == Europe : le Traité de Rome (art. 82) == | ||
Le Traité de Rome, signé en 1957, a établi la Communauté économique européenne (CEE), qui est maintenant intégrée dans l'Union européenne (UE). L'article 82 correspond aujourd'hui à l'article 102 du Traité sur le fonctionnement de l'Union européenne (TFUE), traite de l'abus de position dominante et est un pilier de la politique de concurrence de l'UE. | |||
Cet article vise à empêcher les entreprises qui détiennent une position dominante sur le marché unique européen de s'engager dans des pratiques qui pourraient nuire à la concurrence et aux consommateurs. La position dominante en elle-même n'est pas interdite par le droit de l'UE, mais l'exploitation abusive de cette position l'est. Les pratiques abusives peuvent inclure : | |||
* Imposer des prix ou des conditions de transaction non équitables : Cela peut inclure des prix excessivement élevés ou des conditions commerciales qui placent les partenaires commerciaux ou les consommateurs dans une position désavantageuse. | |||
* Limiter la production ou le développement technique : Cela peut viser à réduire l'offre sur le marché pour maintenir les prix élevés ou à freiner l'innovation qui pourrait être bénéfique pour les consommateurs. | |||
* Appliquer des conditions inégales à des prestations équivalentes : Cela peut entraîner une discrimination entre les partenaires commerciaux, faussant la concurrence. | |||
* Subordonner la conclusion de contrats : Cela peut impliquer d'obliger un partenaire commercial à accepter des obligations supplémentaires qui ne sont pas liées au contrat principal, une pratique connue sous le nom de vente liée. | |||
L'article 102 du TFUE est appliqué par la Commission européenne, qui a le pouvoir d'enquêter et de sanctionner les entreprises pour de telles pratiques. Les sanctions peuvent inclure des amendes substantielles et des ordonnances qui exigent des changements dans les pratiques commerciales des entreprises. | |||
La politique de concurrence de l'UE, y compris l'article 102, est cruciale pour assurer un marché équitable et efficace, encourager l'innovation et protéger les consommateurs. Elle reflète l'engagement de l'UE envers une économie de marché ouverte où la concurrence est libre mais réglementée pour empêcher les abus. | |||
== Suisse : la nouvelle LCart == | == Suisse : la nouvelle LCart == | ||
La loi fédérale sur les cartels et autres restrictions à la concurrence de la Suisse, connue sous le nom de LCart (Loi sur les Cartels), constitue le cadre juridique qui régit la concurrence dans le pays. Contrairement à l'approche de l'Union européenne qui se fonde principalement sur l'interdiction des accords anti-concurrentiels, la LCart suisse se concentre sur la notion d'abus de position dominante. Cela signifie que les accords qui pourraient limiter la concurrence ne sont pas automatiquement illicites en Suisse, à moins qu'il soit démontré qu'ils ont un effet abusif sur le marché. | |||
La révision de 2004 a renforcé l'efficacité de la loi en permettant à la Commission de la Concurrence (Comco) d'imposer des sanctions dès la première infraction. Avant cette révision, des sanctions pouvaient seulement être infligées en cas de récidive. Ce changement montre une volonté d'appliquer la loi de manière plus stricte et de décourager les pratiques anti-concurrentielles dès la première infraction. | |||
La LCart prévoit également un programme de clémence, aligné sur les pratiques dans d'autres juridictions comme l'UE et les États-Unis, qui vise à encourager les entreprises à collaborer avec les autorités. Ce programme permet aux entreprises qui divulguent volontairement leur participation à un cartel et qui coopèrent avec la Comco dans son enquête de bénéficier d'une réduction des amendes qui leur sont imposées. Ce mécanisme incitatif est conçu pour démanteler les cartels en incitant les membres à divulguer des informations, ce qui peut souvent être difficile à obtenir autrement pour les autorités de régulation. | |||
Les sanctions prévues par la LCart sont significatives, avec des amendes pouvant atteindre jusqu'à 10% du chiffre d'affaires réalisé en Suisse pendant les trois dernières années. Cela donne à la loi un poids considérable et assure que les entreprises opérant en Suisse prennent sérieusement leurs obligations de conformité en matière de concurrence. | |||
La LCart et la Comco jouent un rôle clé dans la promotion d'une concurrence équitable en Suisse, en cherchant à prévenir les pratiques qui pourraient nuire aux consommateurs et à l'économie suisse dans son ensemble. La loi est un élément essentiel pour maintenir un marché dynamique et compétitif, en assurant que les entreprises agissent de manière équitable et en prévenant les distorsions de marché. | |||
== LCart: l'abus de position dominante == | == LCart: l'abus de position dominante == | ||
La section de la Loi sur les Cartels (LCart) sur l'abus de position dominante spécifie les pratiques qui sont considérées comme un abus de position dominante sur le marché suisse. Ces pratiques sont interdites car elles peuvent fausser la concurrence et nuire aux consommateurs en limitant le choix ou en augmentant les prix. Voici une explication de chaque pratique illicite : | |||
* Refus d'entretenir des relations commerciales : Cela peut inclure le refus de vendre à ou d'acheter de certains partenaires commerciaux sans justification objective. C'est souvent appelé un "refus de traiter" et peut être utilisé pour exclure des concurrents du marché ou pour punir des partenaires commerciaux pour avoir traité avec des concurrents. | |||
* Discrimination de partenaires commerciaux : Traiter différemment les partenaires commerciaux dans des situations similaires, en particulier en matière de prix ou de conditions commerciales, peut être considéré comme discriminatoire et anticoncurrentiel. | |||
* Imposer des prix ou conditions commerciales inéquitables : Ceci peut se référer à des prix excessivement élevés, des conditions de paiement onéreuses, ou d'autres termes qui mettent une partie à un désavantage injuste. | |||
* Sous-enchère ciblée : Vendre à un prix inférieur au coût dans le but de saper un concurrent spécifique, avec l'intention de l'éliminer du marché, est une pratique anticoncurrentielle connue sous le nom de prédation. | |||
* Limitation de la production, des débouchés ou du développement technique : Cela inclut les actions qui limitent artificiellement l'offre, réduisent les opportunités de vente pour les concurrents ou entravent l'innovation et le progrès technique, souvent pour maintenir des prix élevés. | |||
* Vente liée ou conditionnement : Forcer les partenaires commerciaux à accepter des biens ou services supplémentaires qui ne sont pas liés à l'accord principal peut restreindre la concurrence et créer des barrières à l'entrée. | |||
La LCart, en spécifiant ces pratiques comme illicites, cherche à créer un environnement de marché où la concurrence est basée sur le mérite et la performance, plutôt que sur des stratégies anticoncurrentielles. Les entreprises en position dominante doivent donc agir de manière responsable pour ne pas abuser de leur position et fausser le marché à leur avantage. Cela est crucial pour assurer une concurrence loyale et pour protéger les consommateurs ainsi que les petites et moyennes entreprises qui pourraient autrement être évincées du marché. | |||
= Résumé = | |||
Les marchés oligopolistiques sont caractérisés par un petit nombre d'acteurs économiques, chacun possédant une part significative du marché, ce qui leur confère un pouvoir de marché considérable. Dans un tel contexte, ces firmes ont la capacité de maximiser leurs profits collectifs en agissant conjointement à la manière d'un monopole, c'est-à-dire en formant un cartel. Cependant, l'alignement des stratégies de production individuelles sur l'objectif commun de maximisation du profit est souvent instable, comme le révèle le modèle du dilemme du prisonnier. Ce dernier met en lumière le paradoxe où les entreprises, bien que bénéficiant d'une coopération pour maintenir des prix élevés et des productions limitées, sont individuellement incitées à produire davantage pour accroître leurs parts de marché, ce qui conduit à une baisse des prix et à une augmentation de la production globale, réduisant ainsi les profits du cartel. | |||
Par exemple, dans le cas des accords sur les quotas de production pétrolière entre les pays membres de l'OPEP, chaque pays pourrait augmenter unilatéralement sa production pour gagner plus de revenus à court terme, mais si tous les pays faisaient de même, cela entraînerait une surproduction et une chute des prix du pétrole, nuisant à tous les membres à long terme. | |||
Lorsque le nombre de firmes dans un oligopole augmente, le marché se rapproche du modèle de la concurrence parfaite, où aucun acteur n'a suffisamment de pouvoir pour influencer les prix, résultant en des prix plus bas et des quantités produites qui tendent vers l'optimum social. | |||
Pour prévenir les conséquences négatives des oligopoles et protéger les intérêts des consommateurs, les gouvernements ont établi des réglementations antitrust. Aux États-Unis, le Sherman Antitrust Act de 1890 a été un pas décisif pour contrer les monopoles, comme l'illustre le démantèlement de la Standard Oil de Rockefeller. De manière similaire, le Traité de Rome a posé les fondements de la politique de concurrence en Europe en interdisant l'exploitation abusive d'une position dominante sur le marché, une position qui a été renforcée par des lois telles que l'article 102 du TFUE. En Suisse, la Loi sur les Cartels met l'accent sur l'interdiction des abus de position dominante plutôt que sur l'interdiction des cartels en eux-mêmes, avec des mécanismes comme le programme de clémence pour encourager la collaboration des entreprises en cas d'enquête antitrust. | |||
Ces lois et réglementations ne sont pas statiques ; elles évoluent avec le temps pour s'adapter aux nouvelles dynamiques économiques et aux défis posés par les pratiques commerciales en constante évolution. L'objectif reste cependant le même : maintenir des marchés justes et compétitifs, encourager l'innovation et assurer que les consommateurs bénéficient de prix équitables et de choix diversifiés. | |||
= | [[Fichier:Résumé structure de marché 1.png|400px|vignette|centré|Source: Perloff, 2007. NB: MR = marginal revenu et MC = marginal cost.]] | ||
La table fournie présente un comparatif des caractéristiques principales de quatre types de structures de marché : monopole, oligopole, concurrence monopolistique et concurrence pure et parfaite. Chacune de ces structures est définie par des critères spécifiques concernant la maximisation des profits, le pouvoir de fixation des prix, la puissance sur le marché, les conditions d'entrée, le nombre de firmes, les profits à long terme, la dépendance stratégique, la différenciation des produits et des exemples concrets. | |||
Dans un monopole, une seule entreprise (le monopoleur) est présente sur le marché. Cette entreprise est le seul producteur d'un bien ou d'un service, lui donnant un contrôle total sur les prix – elle est un « price setter ». Le pouvoir de marché, c'est-à-dire la capacité de fixer les prix au-dessus du coût marginal (MC), est maximal dans un monopole. Les conditions d'entrée sont telles qu'aucune autre entreprise ne peut entrer sur le marché, souvent à cause de barrières légales ou naturelles. Un monopole peut faire des profits à long terme (≥ 0), car il n'y a pas de pression concurrentielle qui forcerait les prix à baisser jusqu'au niveau du coût marginal. Les produits peuvent être différenciés, comme dans le cas d'une compagnie de gaz naturel locale, qui pourrait être l'unique fournisseur pour une région donnée. | |||
En contraste, un oligopole se compose de quelques entreprises qui dominent un marché. Chacune possède une part significative du marché, ce qui leur confère un pouvoir de marché et leur permet de fixer des prix au-dessus du coût marginal. L'entrée sur le marché est limitée, mais pas impossible, ce qui signifie que les barrières à l'entrée sont significatives mais pas insurmontables. Les firmes oligopolistiques peuvent maintenir des profits à long terme grâce à leur puissance sur le marché. Les stratégies sont interdépendantes : les décisions d'une entreprise affectent et sont affectées par les décisions des concurrents. Les produits en oligopole peuvent être différenciés, comme dans le cas des fabricants d'automobiles, où les marques se concurrencent sur des bases telles que la qualité, le style et la réputation. | |||
La | La concurrence monopolistique est un terme moyen entre l'oligopole et la concurrence parfaite. Les marchés présentent un grand nombre de firmes, et l'entrée est libre, ce qui signifie que les barrières à l'entrée sont faibles ou inexistantes. Les entreprises peuvent fixer des prix, mais leur pouvoir de marché est limité en raison de la présence de nombreux concurrents proches. Elles peuvent obtenir des profits à court terme, mais à long terme, la concurrence entraîne une érosion des profits (tendant vers zéro). La différenciation des produits est une caractéristique clé de la concurrence monopolistique, permettant aux entreprises de gagner des clients fidèles malgré la présence de nombreux substituts proches. Un exemple classique pourrait être celui des plombiers dans une petite ville, où chacun offre un service légèrement différent. | ||
Enfin, la concurrence pure et parfaite représente un idéal théorique où de nombreuses firmes produisent des biens homogènes. Les entreprises sont des « price takers », ce qui signifie qu'elles n'ont aucun pouvoir de fixation des prix et doivent accepter le prix du marché déterminé par l'offre et la demande globales. L'entrée sur le marché est libre, il y a beaucoup d'entreprises, et les profits à long terme sont nuls en raison de la concurrence intense. Les produits sont indifférenciés, ou "commodités", comme dans le cas des agriculteurs produisant des pommes, où les pommes d'un producteur sont considérées comme équivalentes à celles d'un autre. | |||
Chacune de ces structures de marché a des implications distinctes pour les consommateurs, les entreprises et la politique économique. Par exemple, les monopoles peuvent nécessiter une réglementation pour empêcher l'abus de pouvoir de marché, tandis que les marchés concurrentiels peuvent fonctionner avec peu d'intervention étatique. | |||
= Annexes = | = Annexes = | ||
Version actuelle datée du 3 février 2024 à 13:07
| Professeur(s) | |
|---|---|
| Cours | Introduction à la microéconomie |
Lectures
- Introduction au cours d'introduction à la microéconomie
- Approche méthodologiques au cours d'introduction à la microéconomie
- Les forces du marché : l'offre et la demande
- Les élasticités et ses applications
- Offre, demande et politiques gouvernementales
- Surplus du consommateur et du producteur
- Les externalités et le rôle de l'État
- Les biens publics
- Les coûts de production
- Les entreprises en concurrence parfaite
- Les entreprises en monopole
- Concurrence monopolistique
- Oligopole
- Contrainte et préférences du consommateur
- Choix du consommateur
- Les problèmes d'information et les choix publics
L'oligopole représente un type spécifique de concurrence imparfaite. Cette structure de marché se retrouve dans des secteurs où plusieurs entreprises sont en concurrence, mais sans que cette concurrence ne soit assez intense pour les transformer en "preneuses de prix". La particularité de l'oligopole est le nombre restreint d'acteurs impliqués, engendrant une compétition stratégique et minutieuse entre eux.
Dans ce contexte, on distingue différents cas selon le nombre de participants sur le marché. Par exemple, un duopole implique deux entreprises tandis qu'un oligopole caractérise un marché avec quelques offreurs. Ces marchés, où le nombre de vendeurs est relativement petit, sont qualifiés de marchés concentrés. Cette concentration confère aux entreprises un certain pouvoir de marché, leur permettant de fixer les prix et souvent de pratiquer des tarifs supérieurs aux coûts de production.
Les caractéristiques essentielles de l'oligopole incluent un équilibre délicat entre la coopération et la poursuite des intérêts individuels. Bien que ces entreprises aient le pouvoir d'influencer les prix, ce pouvoir est moindre comparé à un monopole. L'interdépendance des décisions des différents acteurs est un autre trait saillant, où chaque entreprise doit tenir compte des stratégies et actions des autres. La collusion, où les firmes coopèrent pour maximiser leurs profits collectifs, est une possibilité dans un tel marché. Enfin, la théorie des jeux, étudiant le comportement des individus dans des situations stratégiques, est particulièrement pertinente pour analyser le comportement des entreprises en situation d'oligopole, fournissant des insights sur
Maximisation du profit avec et sans coopération[modifier | modifier le wikicode]
Hypothèses[modifier | modifier le wikicode]
L'analyse d'un marché sous les hypothèses énoncées révèle un cadre de marché oligopolistique avec des caractéristiques spécifiques.
Premièrement, l'hypothèse d'atomicité du côté de la demande indique que les consommateurs sont nombreux et aucun d'entre eux n'a suffisamment de pouvoir pour influencer le prix du marché. Cette condition assure que le pouvoir de marché est principalement détenu par les offreurs.
Deuxièmement, la nature homogène du bien implique que tous les produits offerts sur le marché sont identiques ou presque. Dans ce contexte, les entreprises ne peuvent pas se différencier par la qualité, le design ou d'autres caractéristiques du produit. Néanmoins, il est également possible d'avoir un oligopole avec des biens différenciés, connu sous le nom d'oligopole à la Bertrand, où la concurrence se fait principalement sur les prix.
Troisièmement, l'absence de libre-entrée indique que de nouvelles entreprises ne peuvent pas facilement entrer sur le marché, souvent en raison de barrières à l'entrée telles que des coûts de démarrage élevés, des technologies propriétaires ou des réglementations gouvernementales. Cela maintient le nombre d'offreurs à un niveau fixe et faible.
Les offreurs dans ce marché ont un pouvoir de marché significatif, leur permettant de fixer des prix supérieurs au coût marginal. Cela résulte du nombre limité de participants et de l'absence de produits de substitution parfaits.
Enfin, étant donné que le bien est homogène, les stratégies des entreprises se concentrent principalement sur le volume de production. Elles n'engagent pas de dépenses en publicité, en différenciation des prix ou en amélioration de la qualité, car ces aspects ne sont pas pertinents dans un marché où les produits sont indifférenciés.
Dans ce type de marché, les entreprises peuvent s'engager dans un comportement stratégique en ce qui concerne les volumes de production, potentiellement en se coordonnant pour maximiser les profits globaux. Les interactions entre les entreprises sont souvent analysées à l'aide de modèles de théorie des jeux, qui peuvent prédire des issues telles que la fixation de quantités de production pour maximiser les profits collectifs ou la compétition pour une part de marché plus importante.
La demande d'eau potable[modifier | modifier le wikicode]
Un exemple est un scénario de marché pour l'eau potable dans un village avec deux caractéristiques importantes : la demande d'eau et la structure du marché dictée par ses offreurs, UN et DEUX.
La demande d'eau potable est décrite par la fonction , où est la quantité demandée et est le prix. Cette fonction montre que la demande diminue à mesure que le prix augmente, ce qui est typique des marchés de biens courants. La forme inverse, , est la fonction de volonté de payer, indiquant le prix maximal que les consommateurs sont prêts à payer pour une quantité donnée d'eau.
Dans ce village, il y a deux fournisseurs uniques (UN et DEUX) pour l'eau potable. L'eau provient d'une source, et on suppose que le coût marginal de fourniture de cette eau est nul, ce qui signifie que le coût total (CT) est équivalent au coût fixe (CF).
Dans ce cadre, il est intéressant d'examiner comment le prix et la quantité offerte seraient affectés sous deux structures de marché extrêmes : la concurrence parfaite et le monopole.
Concurrence Parfaite : Dans un marché de concurrence parfaite, de nombreux vendeurs et acheteurs participent au marché, et aucun d'entre eux n'a suffisamment de pouvoir pour influencer le prix du marché. Cependant, il n'y a que deux offreurs, ce qui ne correspond pas exactement à une concurrence parfaite. Néanmoins, si UN et DEUX agissaient comme en concurrence parfaite, ils prendraient le prix du marché comme donné et produiraient en fonction de la demande. Le prix se stabiliserait au coût marginal, qui est ici nul.
Monopole : Dans un scénario de monopole, un seul vendeur contrôle l'ensemble du marché. Si UN et DEUX fusionnaient ou si l'un éliminait l'autre pour devenir le seul fournisseur, la structure du marché deviendrait monopolistique. Le monopoleur maximiserait les profits en fixant un prix où le revenu marginal est égal au coût marginal. Cependant, comme le coût marginal est nul, le monopoleur choisirait un prix et une quantité qui maximiseraient ses profits en tenant compte de la fonction de demande du marché .
Dans les deux cas, la dynamique du marché serait influencée par la manière dont UN et DEUX interagissent, soit en concurrence, soit en tant qu'entité monopolistique.
Solution en concurrence parfaite[modifier | modifier le wikicode]
Sous l'hypothèse de concurrence parfaite, le prix sur le marché s'aligne sur le coût marginal. Dans ce cas, comme le coût marginal de l'eau potable est zéro (), le prix serait également nul. À ce prix, la quantité totale consommée serait égale à la quantité totale demandée à un prix nul, soit . Cet équilibre serait considéré comme efficient du point de vue de l'allocation des ressources, car le prix reflète exactement le coût marginal de production.
Cependant, cette situation soulève un paradoxe pratique. Si l'eau est fournie gratuitement (), comment les deux fournisseurs, UN et DEUX, couvriraient-ils leurs coûts fixes et continueraient-ils à opérer? Dans la réalité, même si le coût marginal est nul, il existe des coûts fixes (comme l'entretien de l'infrastructure, les salaires, etc.) qui doivent être couverts pour assurer la viabilité économique des fournisseurs.
Ce paradoxe met en évidence une limitation du modèle de concurrence parfaite dans ce contexte. La concurrence parfaite suppose un grand nombre d'offreurs et d'acheteurs, une information parfaite, une absence de coûts de transaction, et des produits homogènes. Mais dans ce scénario, avec seulement deux offreurs et des coûts fixes non nuls, le modèle de concurrence parfaite ne semble pas être le plus approprié pour décrire de manière réaliste le fonctionnement du marché.
Ainsi, même si théoriquement, sous concurrence parfaite, le prix de l'eau serait nul et la quantité consommée maximale, dans la pratique, d'autres modèles de marché (comme l'oligopole ou le monopole) pourraient être plus pertinents pour analyser et comprendre le comportement des offreurs dans ce marché particulier.
Solution en monopole[modifier | modifier le wikicode]
Dans un régime de monopole où UN et DEUX coopèrent, la situation change radicalement par rapport à un marché en concurrence parfaite. Dans ce cas, le profit est maximisé quand la recette totale du marché est maximale, ce qui est particulièrement pertinent étant donné l'absence de coûts variables dans le scénario.
La maximisation du profit dans un monopole est exprimée par la formule : . Ici, π représente le profit, RT la recette totale, CT le coût total, q la quantité produite, et CF le coût fixe.
Pour trouver le niveau de production qui maximise le profit, on dérive la fonction de profit par rapport à q et on égale le résultat à zéro. Cette condition première d'ordre (CPO) est donnée par . En résolvant cette équation, on obtient et par conséquent, . Ainsi, la recette totale maximale et donc le profit maximal est .
Dans ce cadre de coopération, UN et DEUX pourraient s'accorder pour vendre une quantité totale de 60 unités au prix de 60, se partageant la recette totale de 3600 à parts égales, soit 1800 chacun.
En termes de stratégie de marché, cette coopération pourrait prendre la forme d'une collusion ou d'un cartel :
- Collusion : Cela se produit lorsque les entreprises s'entendent secrètement sur les quantités à produire ou les prix à fixer.
- Cartel : C'est quand des offreurs se regroupent formellement et agissent ensemble, souvent par un accord ouvert et officiel.
Cependant, il est important de noter que, bien que les producteurs en situation d'oligopole puissent être tentés de former des cartels pour réaliser des profits de monopole, ces pratiques sont souvent réglementées ou interdites par les lois antitrust. Ces lois visent à prévenir la restriction de la concurrence et à protéger les intérêts des consommateurs, rendant les accords explicites entre producteurs en oligopole illégaux dans de nombreux pays.
Ce graphique économique typique illustre la situation d'un monopole dans le contexte du marché de l'eau potable. Le graphique est divisé en deux sections principales : la courbe de demande (ou volonté de payer) sur le graphique supérieur, et la courbe de recette totale sur le graphique inférieur.
Dans le graphique supérieur, la droite de demande décroît de gauche à droite, indiquant que moins d'eau sera demandée à mesure que le prix augmente, ce qui est cohérent avec la loi de la demande. Le prix du monopole est fixé à 60, ce qui est le point où la recette marginale (non représentée) serait égale au coût marginal, qui est de zéro dans ce cas. Cela est indiqué par le fait que la droite de demande coupe l'axe des quantités à 120 unités, le maximum que les consommateurs seraient prêts à acheter si l'eau était gratuite, et le prix maximum de 120, où la quantité demandée serait nulle.
Le graphique inférieur montre la recette totale (RT), qui est une parabole avec un sommet au point où la quantité est de 60, ce qui représente la quantité optimale pour le monopoleur à vendre. À ce niveau de production, la recette totale est maximisée à 3600, comme indiqué par le pic de la courbe de recette totale. C'est le résultat de la multiplication du prix par la quantité (60 unités x 60 de prix = 3600 de recette totale).
Le commentaire sur le graphique indique que pour maximiser le profit, qui dans ce cas est égal à la recette totale en raison de l'absence de coûts variables, chaque entreprise devrait produire une quantité de 30 et obtenir un profit de 1800 chacune. Cela suppose que les deux entreprises coopèrent parfaitement, partageant le marché équitablement sous un accord de cartel. Cependant, cette situation pourrait ne pas être stable à long terme en raison de la tentation de tricher sur l'accord pour augmenter sa part du profit, un problème communément associé à la théorie des jeux dans l'étude des oligopoles et des cartels.
Il est également important de noter que, bien que cette configuration puisse être profitable pour les monopolistes, elle n'est pas nécessairement bénéfique pour les consommateurs ni pour le bien-être social. Le prix de 60 est supérieur au coût marginal de l'eau (qui est zéro), et par conséquent, la quantité produite et consommée (60 unités) est inférieure à ce qu'elle serait dans un marché concurrentiel (120 unités). Cela conduit à une perte sèche, où certains consommateurs qui auraient été disposés à payer un prix supérieur au coût marginal n'ont pas accès à l'eau.
Enfin, la législation antitrust serait un obstacle à un tel arrangement dans de nombreuses juridictions, car elle est conçue pour empêcher les entreprises de fixer des prix et de limiter la production de manière anticoncurrentielle.
Incitation à tricher[modifier | modifier le wikicode]
L'incitation à tricher dans un accord de cartel est un problème classique dans l'analyse économique des oligopoles. Dans l'exemple de UN et DEUX, même si les deux entreprises s'accordent initialement pour produire chacune 30 unités et fixer le prix à 60, chacune a une incitation à augmenter sa production secrètement pour capturer une plus grande part du marché.
Si UN décide de produire plus tout en anticipant que DEUX maintiendra sa production à 30 unités, la demande résiduelle à laquelle UN fait face est alors donnée par la nouvelle fonction de demande . Cela signifie que le prix que UN peut fixer diminue à mesure que sa propre quantité produite, , augmente.
La recette totale de UN est donnée par , et la recette marginale est identique en l'absence de coûts marginaux, donc . Pour maximiser son profit, UN déterminerait la quantité de production où la recette marginale égale le coût marginal, ce qui mènerait à .
En produisant 45 unités, UN augmente la quantité totale sur le marché à 75 unités (les 30 de DEUX plus ses 45), ce qui fait baisser le prix à 45 selon la fonction de demande du marché. Malgré la baisse du prix, UN améliore son revenu à , dépassant les 1800 qu'il aurait reçus en se conformant à l'accord de cartel.
Ce scénario démontre la tentation de la triche dans les cartels. Si UN augmente sa production, il peut gagner plus à court terme. Cependant, si DEUX s'aperçoit de la triche de UN et décide également de produire plus, le prix du marché pourrait chuter considérablement, potentiellement au-dessous du niveau optimal pour les deux entreprises. La nature instable des cartels est due à cette incitation à tricher et à la difficulté de maintenir la discipline de cartel, surtout en l'absence de mécanismes d'application et de surveillance. En pratique, la plupart des cartels finissent par échouer à cause de cette incitation interne à la triche, à moins qu'ils ne soient soutenus par des mécanismes de contrôle stricts ou des régulations.
Ce graphique économique illustre la situation où l'entreprise UN envisage de tricher dans un accord de cartel avec l'entreprise DEUX pour le marché de l'eau potable. Le graphique supérieur montre la courbe de demande totale du marché, qui est une ligne droite descendant de 120 à 0 en fonction de la quantité. À côté, il y a une courbe de demande "résiduelle" pour l'entreprise UN, qui commence à 90 au lieu de 120, assumant que DEUX continue de produire 30 unités.
L'entreprise UN réalise qu'en produisant plus que sa part convenue de 30 unités — spécifiquement 45 unités — tout en s'attendant à ce que DEUX continue à produire 30 unités, elle peut augmenter ses profits. La nouvelle quantité totale sur le marché serait de 75 unités, ce qui fait baisser le prix de 60 à 45. Bien que le prix soit plus bas, le profit de UN augmente, car il est calculé en fonction de la quantité qu'elle vend elle-même. Le graphique inférieur illustre la recette totale de UN avec un pic à 2025, qui est supérieur à la recette de 1800 obtenue si chaque entreprise respecte l'accord de produire 30 unités.
La ligne pointillée verticale qui part de 45 unités sur le graphique supérieur et qui touche le point le plus haut de la courbe de recette totale de UN sur le graphique inférieur indique clairement que 45 unités est la quantité optimale pour UN si elle veut maximiser son profit en supposant que DEUX ne change pas sa quantité de production. Cependant, cette action de triche baisse le prix de marché pour les deux entreprises, ce qui signifie que DEUX verra son profit réduit à moins qu'elle ne réagisse.
Cette situation illustre le dilemme central des cartels : bien qu'ils puissent être profitables lorsqu'ils sont respectés, chaque membre a une incitation individuelle à produire plus pour augmenter ses bénéfices personnels. Cela mine l'accord de cartel et peut conduire à son effondrement, avec des conséquences potentiellement négatives pour tous les participants. De plus, si DEUX remarque la triche de UN et décide d'augmenter également sa production, le prix sur le marché pourrait tomber encore plus bas, réduisant les profits pour les deux entreprises.
La situation décrite est un exemple classique du "prisonnier's dilemme" en théorie des jeux, où les acteurs, bien que rationnels et poursuivant leur propre intérêt, aboutissent à un résultat qui n'est pas optimal pour le groupe. Cela démontre la difficulté de maintenir la coopération dans les accords de cartel, surtout en l'absence de mécanismes de surveillance et de punition pour la triche.
Équilibre sans coopération[modifier | modifier le wikicode]
Dans une situation où il n'y a pas de coopération entre UN et DEUX, les deux entreprises entrent dans un cycle de réaction et contre-réaction en ajustant leur production en réponse aux actions de l'autre. Si UN triche en augmentant sa production et que DEUX s'en rend compte, DEUX peut choisir d'augmenter également sa production pour récupérer une partie de son profit perdu. Cette dynamique continue jusqu'à ce qu'un équilibre de duopole soit atteint.
L'équilibre de duopole est défini par la condition où les recettes marginales des deux entreprises sont égales et où aucune n'a intérêt à changer sa quantité de production car cela ne ferait qu'abaisser leur profit marginal. Dans le cas présenté, les conditions d'équilibre de duopole sont exprimées par les équations . En résolvant ces équations, on obtient que les quantités optimales pour les deux entreprises sont . Le prix se stabilise alors à et les recettes totales pour chacune des entreprises sont .
À cet équilibre, les deux entreprises produisent chacune 40 unités et le prix du marché est de 40. Cela se traduit par un profit de 1600 pour chaque entreprise, ce qui est inférieur au profit qu'elles auraient pu réaliser si elles avaient maintenu l'accord de cartel et coopéré pour maintenir le prix à 60, générant ainsi un profit de 1800 chacune.
Ce résultat illustre un aspect central des oligopoles : lorsque les entreprises ne coopèrent pas, elles finissent par être pénalisées par la concurrence qu'elles se font mutuellement. L'équilibre de duopole mène à un résultat où chaque entreprise gagne moins que ce qu'elle aurait pu obtenir dans un accord de cartel. Néanmoins, cet équilibre est plus stable que le cartel parce qu'il n'y a pas d'incitation à dévier unilatéralement, puisque toute tentative d'augmenter la production réduirait la recette marginale de l'entreprise concernée.
L'équilibre de duopole reflète un compromis entre la concurrence et la coopération. Bien qu'il ne soit pas aussi profitable pour les entreprises qu'une collusion totale, il est conforme aux lois antitrust et tend à être plus avantageux pour les consommateurs, car il résulte en un prix inférieur et une quantité supérieure par rapport à ce qui serait observé sous un cartel.
Ce graphique représente la continuation de l'analyse économique du marché de l'eau potable dans une situation de duopole sans coopération, où les entreprises UN et DEUX ajustent leur production en réponse aux actions de l'autre jusqu'à atteindre un équilibre.
Le graphique supérieur montre les courbes de demande totale et résiduelle pour l'entreprise UN. La courbe de demande résiduelle démarre à un prix de 80 pour zéro quantité, supposant que DEUX produit 40 unités (comme indiqué par le point où la courbe résiduelle rencontre l'axe vertical). La courbe de demande totale décrit la volonté de payer pour l'ensemble du marché et décroît en fonction de la quantité totale. L'intersection de la quantité produite par UN et la demande résiduelle détermine le prix sur le marché.
Le graphique inférieur illustre les recettes totales (RT) pour l'entreprise UN avec une courbe en forme de parabole, atteignant son sommet à 40 unités produites par UN, ce qui correspond à la recette totale et donc au profit maximal lorsque DEUX produit également 40 unités. Le profit de chaque entreprise dans le duopole est illustré par le niveau de 1600, inférieur au profit de 2025 pour UN lorsqu'elle a triché et produit 45 unités, mais plus élevé que le profit de 1350 de DEUX lorsque UN a produit 45 et DEUX est restée à 30.
Le commentaire sur l'image indique que DEUX reconnaît que son profit a diminué en raison de la baisse du prix (à 45) lorsque UN a augmenté sa production, et donc DEUX augmente également sa production pour compenser. Finalement, les deux entreprises s'ajustent pour atteindre un équilibre où elles produisent chacune 40 unités, conduisant à un prix de marché de 40 et à un profit de 1600 pour chacune.
Cette situation d'équilibre en duopole montre que, même si les entreprises pourraient potentiellement gagner plus en coopérant (comme dans le cartel où elles gagnaient 1800 chacune), la tentation de tricher et l'absence de mécanismes de coopération les conduisent à un résultat où elles gagnent moins. Cependant, cet équilibre est plus stable car aucun des duopolistes n'a d'incitation à changer sa production, puisque toute augmentation réduirait le prix et donc les profits.
L'image illustre le concept d'équilibre de Nash dans le contexte d'un duopole, où chaque entreprise, en prenant en compte la stratégie de l'autre, choisit sa meilleure réponse. Cet équilibre n'est pas l'optimal de Pareto, car il y a une perte sèche due au fait que le prix est supérieur au coût marginal (qui est de zéro), et donc la quantité produite est inférieure à ce qu'elle serait dans un marché parfaitement concurrentiel. Cela révèle la tension intrinsèque dans les marchés oligopolistiques entre les incitations individuelles et le bien-être collectif.
Maximisation du profit en duopole : cas général[modifier | modifier le wikicode]
Dans un duopole, la maximisation du profit est un problème classique d'interaction stratégique entre deux entreprises. Chaque entreprise cherche à maximiser ses profits en tenant compte non seulement de ses propres coûts et de la demande du marché, mais également des actions de son concurrent.
Pour l'entreprise 1, la maximisation du profit est donnée par l'équation , où est la quantité produite par l'entreprise 1, est le prix du marché en fonction de la quantité totale offerte sur le marché, et sont les coûts totaux de l'entreprise 1. Ici, est la somme des quantités produites par les deux entreprises, soit .
La condition de premier ordre (CPO) pour la maximisation du profit pour l'entreprise 1, où la recette marginale est égale au coût marginal , est exprimée par . Cette équation montre que le coût marginal de l'entreprise 1 doit être égal au prix plus la variation du prix multipliée par la quantité produite par l'entreprise 1.
De même, pour l'entreprise 2, la maximisation du profit est exprimée par , avec une condition de premier ordre similaire à celle de l'entreprise 1 : .
L'aspect le plus crucial de ces équations est qu'elles illustrent l'interdépendance entre les entreprises dans un duopole. Les décisions de quantité de l'une affectent le prix de marché, qui à son tour affecte la recette marginale et donc les décisions de l'autre entreprise. En pratique, cela signifie que chaque entreprise doit anticiper la réaction de l'autre lorsqu'elle prend ses décisions de production.
En résumé, dans un duopole, chaque entreprise doit tenir compte non seulement de ses propres coûts de production et de la demande du marché, mais aussi des actions de son concurrent. L'équilibre du marché est atteint lorsque les deux entreprises ont ajusté leur production de manière à ce que leurs recettes marginales soient égales à leurs coûts marginaux, prenant en compte les effets de leurs propres actions sur le prix du marché et donc sur les recettes marginales de l'autre. Cela conduit à un équilibre de Cournot dans lequel chaque entreprise produit une quantité telle que sa recette marginale est égale à son coût marginal, en tenant compte de la production de l'autre entreprise.
Équilibre de l'oligopole[modifier | modifier le wikicode]
Dans un oligopole où les entreprises agissent individuellement et sans coopération pour déterminer leur niveau de production, les résultats sont typiquement intermédiaires entre ceux d'un monopole et d'une concurrence parfaite.
La quantité totale produite dans un oligopole est généralement plus importante que celle produite sous un monopole mais reste inférieure à la quantité qui serait produite dans un marché en concurrence parfaite. Ceci est dû à l'effet de l'interdépendance entre les firmes oligopolistiques : chaque firme, en maximisant son profit, ne prend pas en compte l'impact de sa production sur les bénéfices des autres firmes, à l'inverse d'un monopole qui contrôle l'ensemble de la production du marché.
Le prix établi par les firmes en oligopole tend à être inférieur au prix de monopole, car la présence de concurrents sur le marché pousse les prix vers le bas. Cependant, ce prix reste supérieur au prix qui prévaudrait sous une concurrence parfaite. En concurrence parfaite, le prix du marché correspondrait au coût marginal (Cm), car les entreprises sont des preneuses de prix et ne peuvent fixer leurs prix au-dessus du coût marginal sans perdre toute leur clientèle.
Les profits réalisés par les entreprises en oligopole sont également intermédiaires. Ils sont plus élevés que ce qu'ils seraient dans un marché en concurrence parfaite, où les profits économiques tendent vers zéro à long terme, mais ils sont inférieurs à ceux qu'une entreprise monopolistique pourrait réaliser. Cela s'explique par le fait qu'en concurrence parfaite, les entreprises ne peuvent pas fixer de prix au-dessus du coût marginal en raison de la présence de nombreux concurrents, tandis qu'en oligopole, le nombre réduit de concurrents confère un certain pouvoir de marché, permettant aux entreprises de maintenir les prix à un niveau supérieur au coût marginal et de réaliser ainsi un mark-up positif.
En résumé, l'équilibre de l'oligopole se caractérise par un niveau de production, de prix et de profits qui reflètent le pouvoir de marché détenu par les entreprises oligopolistiques. Ce pouvoir de marché leur permet de fixer les prix au-dessus du coût marginal, réalisant ainsi un profit supérieur à celui d'un environnement de concurrence parfaite, mais sans atteindre les niveaux de profit qu'un monopole pourrait obtenir.
L'effet de la taille[modifier | modifier le wikicode]
L'augmentation du nombre de vendeurs dans un marché oligopolistique a tendance à pousser le marché vers des résultats similaires à ceux d'une concurrence parfaite. Cet effet peut être analysé à travers deux mécanismes principaux : l'effet quantité et l'effet prix.
L'effet quantité est lié au fait que, dans un marché oligopolistique, le prix est généralement fixé au-dessus du coût marginal. Cela signifie que chaque unité supplémentaire vendue au prix courant va augmenter les profits, car le revenu généré par la vente de l'unité supplémentaire est supérieur au coût de sa production. Si le nombre de vendeurs augmente, la quantité totale offerte sur le marché va augmenter, ce qui devrait logiquement augmenter les profits globaux, toutes choses étant égales par ailleurs.
L’effet prix concerne la baisse du prix qui résulte de l'augmentation de l'offre totale sur le marché. En effet, l'augmentation de la production totale peut saturer le marché et entraîner une baisse du prix en raison de la concurrence accrue entre les vendeurs. Cette baisse de prix va réduire le profit réalisé sur chaque unité vendue.
Lorsque le nombre de vendeurs augmente, ces deux effets s'opposent. L'effet quantité cherche à augmenter les profits en vendant plus d'unités, tandis que l'effet prix tend à les diminuer en réduisant les revenus par unité. L'effet net sur les profits dépendra de la sensibilité de la demande aux changements de prix (l'élasticité de la demande) et de la capacité de production supplémentaire à influencer le marché.
À mesure que le nombre de vendeurs augmente, l'effet prix devient de plus en plus dominant. Les prix commencent à baisser, se rapprochant du coût marginal. Cela diminue le pouvoir de marché de chaque vendeur et réduit les profits par unité. En théorie, si le nombre de vendeurs continue d'augmenter indéfiniment, le marché deviendrait parfaitement concurrentiel, le prix convergerait vers le coût marginal, et la quantité produite se rapprocherait du niveau socialement efficace, c'est-à-dire là où le prix égale le coût marginal.
Dans un marché socialement efficace, les ressources sont allouées de la manière la plus avantageuse possible, maximisant le bien-être total des consommateurs et des producteurs. L'augmentation du nombre de vendeurs dans un marché oligopolistique peut donc mener à une allocation des ressources plus efficace, à des prix plus bas pour les consommateurs et à une augmentation de la quantité vendue, ce qui est bénéfique pour la société dans son ensemble.
La théorie des jeux et l'économie de la coopération[modifier | modifier le wikicode]
Eléments de théorie des jeux[modifier | modifier le wikicode]
La théorie des jeux est une branche mathématique et économique qui modélise et analyse comment les agents économiques prennent des décisions stratégiques dans des situations où les résultats dépendent non seulement de leurs propres décisions, mais aussi de celles des autres agents. Elle trouve des applications dans divers domaines tels que l'économie, la politique, la psychologie, la biologie et même dans les relations internationales.
Dans le contexte de la théorie des jeux, une stratégie est un plan d'action complet qui spécifie le comportement à adopter dans toutes les situations possibles qui pourraient survenir. Cela pourrait impliquer une stratégie pure, où un joueur choisit une seule action spécifique, ou une stratégie mixte, où un joueur rend ses actions aléatoires en utilisant une distribution de probabilités sur plusieurs actions possibles.
Les jeux peuvent être catégorisés comme statiques ou dynamiques. Dans un jeu statique, tous les joueurs choisissent leurs actions simultanément, ou du moins sans connaître les actions des autres. Les jeux dynamiques, quant à eux, se déroulent sur plusieurs périodes avec des actions à des moments différents, ce qui permet aux joueurs d'observer certaines des actions précédentes des autres joueurs avant de décider de leur propre stratégie. Cela peut introduire des considérations de réputation et de punition pour non-coopération, comme dans le dilemme des prisonniers répété.
L'incertitude joue également un rôle clé dans la théorie des jeux. Dans beaucoup de jeux, les joueurs n'ont pas une information parfaite concernant les stratégies ou les types des autres joueurs. Cela mène à des stratégies où les joueurs doivent maximiser leurs gains attendus en tenant compte des probabilités des différentes actions des autres joueurs.
La notion de stratégies crédibles est essentielle dans les jeux dynamiques. Une stratégie est dite crédible si un joueur a des incitations à s'y tenir même après que les étapes initiales du jeu se soient déroulées. Cela est souvent lié au concept d'engagement et aux menaces ou promesses dans des jeux séquentiels.
La théorie des jeux utilise des outils mathématiques avancés pour résoudre des jeux et trouver des équilibres stratégiques, comme l'équilibre de Nash, où aucun joueur ne peut augmenter son gain attendu en changeant unilatéralement sa stratégie, en supposant que les autres joueurs maintiennent leurs stratégies constantes. La théorie des jeux aide à comprendre les comportements complexes en situation d'interdépendance et elle est fondamentale pour analyser les marchés économiques, en particulier les oligopoles, où les entreprises doivent constamment anticiper et réagir aux stratégies de leurs concurrents.
Théorie des jeux et oligopole[modifier | modifier le wikicode]
L'oligopole est un terrain classique pour l'application de la théorie des jeux en raison du nombre limité de firmes et de l'interdépendance de leurs décisions. Dans un tel marché, chaque entreprise doit prendre en compte les réactions potentielles de ses concurrents lorsqu'elle prend ses propres décisions de production et de tarification.
Chaque entreprise, ou "joueur" dans le langage de la théorie des jeux, cherche à maximiser son profit. Cependant, contrairement à un marché en concurrence parfaite où chaque entreprise est une preneuse de prix et où son action individuelle n'a pas d'impact sur le marché, ou à un monopole où l'entreprise a un contrôle total sur le marché, chaque firme en oligopole sait que ses actions influenceront et seront influencées par les actions de ses concurrents. C'est un exemple de jeu à somme non nulle, où les profits de l'une ne sont pas forcément les pertes des autres, et les stratégies optimales dépendent fortement des choix des autres joueurs.
Dans un marché oligopolistique, les entreprises peuvent opérer sous une information complète mais imparfaite. Information complète signifie que toutes les entreprises connaissent toutes les stratégies possibles et les payoffs associés à chaque combinaison de stratégies pour tous les joueurs. Cependant, l'information est imparfaite car, bien que chaque entreprise connaisse les payoffs et les stratégies, elle ne connaît pas les choix de stratégie que les autres entreprises feront ou ont fait.
La simultanéité des actions ajoute à la complexité stratégique. Chaque entreprise doit choisir son niveau de production et son prix sans savoir précisément ce que les autres vont faire. Cela peut conduire à des résultats variés, y compris des équilibres précaires qui peuvent être perturbés par des changements dans les stratégies des entreprises ou des entrées de nouvelles firmes sur le marché.
Le concept d'équilibre de Nash est particulièrement pertinent ici : c'est une situation où, connaissant les stratégies des autres, aucune entreprise n'a intérêt à changer unilatéralement sa propre stratégie. Cet équilibre reflète une sorte de trêve stratégique où chaque entreprise, en supposant que les autres ne changent pas leur stratégie, choisit la meilleure réponse à ces stratégies.
En pratique, cela peut mener à des stratégies qui incluent des compromis entre agressivité et prudence, l'adoption de stratégies de signalisation, ou des tentatives de coopération tacite pour éviter des guerres de prix destructrices. La théorie des jeux fournit donc un cadre pour comprendre et prédire les comportements dans ces marchés complexes.
L'équilibre de Nash[modifier | modifier le wikicode]
John F. Nash a apporté une contribution fondamentale à la théorie des jeux avec sa caractérisation de l'équilibre pour les jeux non coopératifs. Cet équilibre, connu sous le nom d'équilibre de Nash, est devenu un concept central de la théorie des jeux moderne et a des applications dans de nombreux domaines allant de l'économie à la biologie et au-delà.
L'équilibre de Nash est une situation où aucun joueur n'a intérêt à changer de stratégie tant que les autres joueurs maintiennent les leurs. Cela signifie que, même si les joueurs ne coopèrent pas ou ne communiquent pas entre eux, ils arrivent à un état où les stratégies sont mutuellement les meilleures réponses les unes aux autres. Chaque joueur, en regardant ce que font les autres, choisit la meilleure stratégie possible pour lui-même.
Il est crucial de noter que l'équilibre de Nash ne correspond pas nécessairement à l'optimalité du point de vue du groupe ou du bien-être social. Dans certains jeux, comme le célèbre dilemme du prisonnier, l'équilibre de Nash peut conduire à un résultat sous-optimal pour tous les participants. Cela est dû au fait que l'équilibre de Nash reflète ce qui est meilleur pour chaque individu dans le contexte des choix des autres, mais pas nécessairement ce qui est optimal pour l'ensemble des joueurs.
Quand un joueur a une stratégie dominante, elle lui donnera le meilleur résultat peu importe ce que les autres joueurs décident de faire. Si tous les joueurs ont une stratégie dominante, l'équilibre de Nash est simple à trouver : chaque joueur choisira sa stratégie dominante. Cependant, dans de nombreux jeux plus complexes, les joueurs n'ont pas de stratégies dominantes et doivent tenir compte de manière plus nuancée des stratégies potentielles des autres joueurs pour déterminer leur meilleure réponse.
L'équilibre de Nash a été une avancée importante car il fournit un moyen de prédire les résultats dans des situations où les individus prennent des décisions qui sont interdépendantes, ce qui est un aspect commun à de nombreuses situations économiques, sociales et biologiques. La reconnaissance de l'importance de ce concept par le Comité Nobel souligne son influence étendue et sa pertinence pour les sciences sociales.
Le dilemme du prisonnier[modifier | modifier le wikicode]
Le dilemme du prisonnier est un exemple classique en théorie des jeux qui démontre le conflit entre les intérêts individuels et le bien-être collectif. C'est un jeu non coopératif où, malgré l'existence d'un résultat coopératif qui serait meilleur pour les deux parties, l'équilibre de Nash prédit un résultat non coopératif où chaque joueur opte pour sa stratégie dominante, conduisant à un résultat sous-optimal pour les deux.
Le jeu se déroule habituellement comme suit : deux criminels présumés sont arrêtés et interrogés séparément. Chacun a la possibilité de trahir l'autre en avouant, ou de coopérer avec l'autre en restant silencieux. Si l'un trahit et l'autre reste silencieux, le traître est libéré tandis que l'autre reçoit la peine maximale. Si tous deux trahissent, ils reçoivent tous les deux une peine sévère, mais moins que la peine maximale. Si tous deux restent silencieux, ils reçoivent tous les deux une peine plus légère.
Le dilemme réside dans le fait que, bien que la coopération (tous les deux restent silencieux) conduirait à un meilleur résultat global, la stratégie dominante pour chaque joueur est de trahir l'autre. En effet, peu importe ce que fait l'autre joueur, chaque joueur a une meilleure issue en trahissant : soit il est libéré (si l'autre coopère), soit il reçoit une peine moins lourde (si l'autre trahit également). Par conséquent, l'équilibre de Nash est que les deux joueurs trahissent, résultant en une peine plus lourde pour les deux, ce qui est un résultat pire que si les deux avaient coopéré.
Dans le contexte des marchés oligopolistiques, le dilemme du prisonnier illustre pourquoi les firmes ont du mal à maintenir la coopération, comme dans le cas d'un cartel où les firmes pourraient bénéficier de profits plus élevés en limitant la production pour maintenir les prix élevés. Malgré ces avantages potentiels, la tentation de trahir le cartel en produisant plus pour augmenter sa propre part de marché rend la coopération instable. Chaque firme sait que si elle ne trahit pas et que l'autre le fait, elle se retrouvera avec le pire résultat possible. Ainsi, le manque de confiance et l'incitation à agir dans son propre intérêt poussent les firmes vers la non-coopération, souvent au détriment du bien-être collectif.
Le dilemme du prisonnier est un exemple emblématique de la théorie des jeux qui montre comment les intérêts individuels peuvent entrer en conflit avec l'intérêt collectif, même quand la coopération serait bénéfique pour tous les participants.
Dans ce scénario, les deux prisonniers sont confrontés à un choix sans la possibilité de coordonner leurs actions. Le tableau des payoffs pour ce jeu peut être décrit comme suit :
- Si aucun des deux prisonniers n'avoue (coopération mutuelle), ils écopent tous les deux d'une peine mineure d'un an.
- Si l'un avoue (trahit) et l'autre non, le traître est relâché tandis que celui qui reste silencieux est sévèrement puni avec vingt ans de prison.
- Si les deux avouent (défaut mutuel), ils reçoivent tous les deux une peine de huit ans de prison.
La difficulté vient du fait que chaque prisonnier doit prendre une décision sans savoir ce que l'autre va faire. La stratégie dominante (la meilleure action à prendre quelle que soit l'action de l'autre joueur) pour chacun est d'avouer, car cela maximise l'utilité individuelle quel que soit le choix de l'autre prisonnier. Ainsi, l'équilibre de Nash dans ce jeu est pour les deux prisonniers d'avouer, car en faisant ce choix, aucun des deux ne peut améliorer sa situation en changeant unilatéralement sa décision.
Cependant, l'équilibre de Nash n'est pas l'optimum de Pareto dans ce cas. L'optimum de Pareto est une situation où il n'est pas possible d'améliorer la situation de quelqu'un sans détériorer celle d'un autre. Si les deux prisonniers pouvaient s'entendre pour ne pas avouer, ils seraient tous les deux mieux lotis avec seulement un an de prison chacun. Mais, en raison de l'impossibilité de communiquer et de l'incertitude concernant les actions de l'autre, ils finissent par choisir une stratégie qui les conduit à un résultat mutuellement défavorable.
Le dilemme du prisonnier illustre bien le défi de la coopération dans de nombreuses situations économiques, politiques et sociales, où la confiance et la communication sont essentielles pour atteindre des résultats mutuellement avantageux. Il démontre également la complexité des interactions humaines et la difficulté de prendre des décisions rationnelles dans des situations d'incertitude.

La matrice des payoffs fournie représente les résultats possibles du dilemme du prisonnier pour deux suspects, "Brute" et "Truand". Chaque suspect a deux options : avouer ou se taire. Les payoffs sont exprimés en termes d'années de prison que chaque suspect encourt en fonction de la décision prise, à la fois par lui-même et par l'autre.
Analysons les payoffs :
- Si les deux avouent, chacun reçoit une peine de 8 ans de prison.
- Si Brute avoue mais que Truand se tait, Brute est libéré et Truand reçoit la peine maximale de 20 ans de prison.
- Si Brute se tait mais que Truand avoue, Brute reçoit la peine maximale de 20 ans de prison et Truand est libéré.
- Si les deux se taisent, chacun reçoit une peine mineure d'1 an de prison.
Le dilemme se situe dans le fait que bien que le meilleur résultat collectif soit atteint lorsque les deux se taisent (1 an de prison chacun), la décision rationnelle pour chaque individu, lorsque l'on considère les actions de l'autre comme données, est d'avouer. Ainsi, si Truand pense que Brute va se taire, il devrait avouer pour être libéré. De même, si Truand pense que Brute va avouer, il devrait aussi avouer pour éviter la peine de 20 ans. La même logique s'applique à Brute. Par conséquent, l'équilibre de Nash de ce jeu est que les deux avouent, puisque avouer est la meilleure réponse pour chaque suspect quel que soit le choix de l'autre.
Cet équilibre de Nash est unique et il est non-optimal car il mène à un résultat où les deux joueurs obtiennent un payoff pire que s'ils avaient choisi de se taire. Cela illustre la difficulté de maintenir la coopération, car bien que coopérer soit mutuellement avantageux, elle n'est pas un choix rationnel au niveau individuel sans une communication et une confiance entre les joueurs.
La symétrie de ce jeu signifie que les payoffs sont identiques pour les stratégies miroirs des deux joueurs. Cependant, la théorie des jeux s'applique également à des jeux non symétriques où les stratégies et les payoffs peuvent varier d'un joueur à l'autre, ce qui peut complexifier davantage l'analyse et la détermination des équilibres.
Un jeu de course à l'armement[modifier | modifier le wikicode]
Un jeu de course à l'armement est un exemple classique de dilemme de sécurité qui se produit souvent dans les relations internationales et peut être analysé à l'aide de la théorie des jeux. Dans ce scénario, deux pays (ou plus) doivent décider s'ils doivent augmenter leur arsenal militaire. Bien que chaque pays puisse bénéficier individuellement d'une position plus forte en s'armant davantage, si tous les pays choisissent de s'armer, cela pourrait conduire à une augmentation des tensions, à une instabilité régionale et, dans le pire des cas, à un conflit armé.
Voici comment un jeu de course à l'armement pourrait être structuré en termes de théorie des jeux :
- Les Joueurs : Deux pays, Pays A et Pays B.
- Les Stratégies : Chaque pays a deux options - s'armer ou ne pas s'armer.
- Les Payoffs : Les gains sont déterminés non seulement par la décision d'un pays de s'armer ou non, mais aussi par la décision prise par l'autre pays.
Les résultats possibles sont les suivants :
- Désarmement Mutuel : Si les deux pays choisissent de ne pas s'armer, ils évitent les coûts liés à une course aux armements et peuvent bénéficier d'une plus grande stabilité et de relations pacifiques. Cependant, ils peuvent se sentir vulnérables à des menaces extérieures.
- Course aux Armements : Si les deux pays choisissent de s'armer, cela augmente les dépenses militaires et la tension, réduisant potentiellement la sécurité globale.
- Déséquilibre : Si un pays s'arme et que l'autre ne le fait pas, le pays armé pourrait se sentir plus en sécurité avec un avantage militaire, tandis que le pays désarmé pourrait se sentir vulnérable et désavantagé.
- Stabilité de Nash : L'équilibre de Nash dans ce jeu est souvent la situation où les deux pays s'arment, car chaque pays a la stratégie dominante de s'armer pour garantir sa sécurité quelles que soient les actions de l'autre.
L'ironie de la course à l'armement est que, bien que chaque pays cherche à augmenter sa propre sécurité en s'armant, l'armement mutuel peut en fait réduire la sécurité globale, un concept connu sous le nom de paradoxe de la sécurité. Ce paradoxe est semblable au dilemme du prisonnier en ce que les résultats individuellement rationnels conduisent à un résultat collectivement irrationnel ou sous-optimal.
Dans la réalité, ces jeux sont souvent répétés ou dynamiques, avec une histoire de mouvements précédents qui peuvent influencer les stratégies actuelles. En outre, les éléments tels que les alliances, les traités et les organismes internationaux peuvent jouer un rôle dans la modification des payoffs et des choix stratégiques disponibles pour les pays.
L'image montre une matrice de payoff pour un jeu de course à l'armement entre deux superpuissances historiques, l'URSS et les États-Unis. La matrice représente les conséquences de deux stratégies disponibles pour chacun des acteurs : "s'armer" ou "se désarmer". Les résultats sont basés sur la combinaison des choix des deux pays.
Analysons les payoffs dans chaque scénario :
- Si l'URSS et les États-Unis choisissent tous les deux de "s'armer", ils sont tous deux "soumis au risque", ce qui implique une augmentation des tensions et une sécurité réduite en raison de la probabilité accrue de confrontation militaire.
- Si l'URSS décide de "s'armer" tandis que les États-Unis choisissent de "se désarmer", l'URSS est "en sécurité et puissante" tandis que les États-Unis sont "soumis au risque et affaiblis". Cela donne un avantage stratégique à l'URSS, laissant les États-Unis vulnérables.
- Si l'URSS choisit de "se désarmer" tandis que les États-Unis décident de "s'armer", les rôles sont inversés avec les États-Unis en position de sécurité et de puissance, et l'URSS soumise au risque et affaiblie.
- Si les deux décident de "se désarmer", ils sont tous les deux "en sécurité", ce qui serait l'issue la plus pacifique et la plus stable, réduisant le risque d'un conflit armé.
La stratégie dominante pour les deux joueurs dans ce jeu, similaire à la stratégie "avoue" dans le dilemme du prisonnier classique, est de "s'armer". Indépendamment de la décision prise par l'autre partie, chaque pays a un meilleur résultat (en termes de sécurité et de pouvoir) lorsqu'il choisit de s'armer. Par conséquent, l'équilibre de Nash de ce jeu est que les deux pays finissent par s'armer, car aucune des parties n'a un incitatif unilatéral à se désarmer. Cependant, tout comme dans le dilemme du prisonnier, cet équilibre n'est pas socialement optimal ; les deux pays seraient mieux si tous les deux choisissaient de se désarmer, réduisant ainsi les risques de conflit tout en économisant des ressources dépensées dans l'armement.
Cet exemple illustre clairement le paradoxe de la sécurité : en cherchant à augmenter leur sécurité par des moyens militaires, les pays peuvent en fait diminuer leur sécurité globale en raison de la réaction réciproque et de la méfiance qu'elle génère. Cela démontre la complexité de la coopération internationale et les défis associés à la prise de décisions dans un environnement international souvent incertain et basé sur la perception des actions des autres.
Le duopole comme dilemme du prisonnier[modifier | modifier le wikicode]
Le duopole peut être conceptualisé comme un dilemme du prisonnier, où deux entreprises (ou duopolistes) sont confrontées à la décision de coopérer pour maximiser leurs profits collectifs ou de concurrencer agressivement pour maximiser leurs profits individuels. Si les deux entreprises coopèrent, elles peuvent agir de concert pour fixer des prix élevés et limiter leur production, se comportant essentiellement comme un monopole et se partageant les profits maximaux possibles. Cependant, la tentation d'augmenter la part de marché individuelle en produisant plus et en vendant à un prix inférieur peut mener à un résultat non coopératif, qui est moins avantageux pour les deux.
Dans la structure d'un duopole, chaque entreprise doit prendre en compte les actions potentielles de son concurrent lorsqu'elle prend ses décisions stratégiques. La théorie des jeux prédit que si chaque entreprise poursuit son intérêt individuel sans accord contraignant de coopération, elles finiront toutes les deux par produire plus, baisser les prix, et voir leurs profits diminuer par rapport à ce qu'ils auraient été sous coopération. Cela est dû au fait que chaque entreprise vise à maximiser son propre profit sans tenir compte de l'impact de ses actions sur le profit global du marché, ce qui peut conduire à une surproduction et à une diminution des prix.
L'équilibre de Nash dans un tel duopole est similaire au dilemme du prisonnier, où chaque entreprise choisit de ne pas coopérer (c'est-à-dire produire plus et baisser les prix) car cette stratégie maximise son profit étant donné la stratégie de l'autre entreprise. C'est l'équilibre stable car si une entreprise dévie et réduit sa production dans l'espoir d'augmenter les prix, elle risque de perdre des parts de marché si l'autre entreprise ne suit pas. Ainsi, même si les deux entreprises seraient mieux loties en coopérant, la nature non contraignante de leur interaction et le manque de communication et de confiance mutuelle les mènent à un équilibre non coopératif.
Cependant, il est important de noter que dans le monde réel, les entreprises en oligopole peuvent trouver des moyens de surmonter ce dilemme par divers moyens, tels que la formation de cartels, l'établissement de règles de concurrence tacites ou l'adoption de stratégies de différenciation de produits, qui peuvent les aider à maintenir des prix élevés et à se rapprocher de la profitabilité du monopole. Ces méthodes, cependant, peuvent être limitées par des lois antitrust et d'autres régulations visant à maintenir la concurrence sur les marchés.
L'image représente une matrice de payoff qui illustre un jeu de duopole entre l'Iran et l'Arabie saoudite, centré sur leur décision de production pétrolière. Chaque pays a la possibilité de choisir entre une production élevée ou faible. Les payoffs sont exprimés en milliards de dollars, reflétant probablement le profit ou le revenu que chaque pays s'attend à gagner en fonction de la combinaison de leurs décisions de production.
Lorsque les deux pays choisissent une production élevée, l'Arabie saoudite et l'Iran gagnent chacun 40 milliards de dollars. Cette situation peut être interprétée comme une surproduction qui entraîne une baisse des prix du pétrole sur le marché mondial, réduisant ainsi les revenus pour les deux producteurs.
Si l'Iran augmente sa production tandis que l'Arabie saoudite réduit la sienne, l'Iran gagne plus (60 milliards de dollars) tandis que l'Arabie saoudite voit ses revenus diminuer à 30 milliards de dollars. L'inverse est également vrai : si l'Iran réduit sa production et que l'Arabie saoudite augmente la sienne, l'Iran obtient 30 milliards de dollars et l'Arabie saoudite 60 milliards de dollars.
Dans le cas où les deux pays décident de réduire leur production, l'Arabie saoudite gagne 50 milliards de dollars et l'Iran 30 milliards de dollars. Cela peut refléter des prix plus élevés en raison d'une offre réduite, mais avec une part de marché plus grande pour l'Arabie saoudite, expliquant pourquoi ses revenus sont plus élevés que ceux de l'Iran.
L'équilibre de Nash dans ce jeu, en supposant que chaque joueur agit rationnellement et en connaissant les stratégies de l'autre, serait pour les deux pays de choisir une production élevée. C'est parce que, quelle que soit la décision de l'autre pays, chaque pays a un meilleur payoff en choisissant une production élevée (passant de 30 à 40 milliards si l'autre se désarme, et de 50 à 60 milliards si l'autre augmente également sa production).
Cependant, cet équilibre de Nash n'est pas l'optimum de Pareto. Les deux pays seraient collectivement mieux lotis si tous deux choisissaient de limiter leur production, car ils pourraient potentiellement augmenter leurs profits globaux grâce à des prix plus élevés pour leur pétrole. Cependant, sans un accord de coopération qui serait contraignant pour les deux parties, l'intérêt individuel incite chaque pays à augmenter sa production, menant à un équilibre moins avantageux pour tous les deux, similaire à la dynamique observée dans le dilemme du prisonnier.
Un jeu de publicité[modifier | modifier le wikicode]
Cette matrice de payoff décrit un jeu de stratégie de publicité entre deux entreprises concurrentes, Camel et Marlboro. Chacune de ces entreprises doit décider si elle doit faire de la publicité ou non. Les profits résultants pour chaque entreprise dépendent de leur choix de stratégie combiné avec le choix de l'autre entreprise.
Les profits sont les suivants selon les décisions prises par Camel et Marlboro :
- Si Camel et Marlboro choisissent tous deux de faire de la publicité, ils gagnent chacun 3 milliards de dollars. Cela pourrait signifier que les coûts de la publicité érodent une partie des profits additionnels qu'ils pourraient obtenir grâce à l'augmentation des ventes.
- Si Camel fait de la publicité tandis que Marlboro ne le fait pas, Camel gagne 5 milliards de dollars et Marlboro seulement 2 milliards de dollars. Cela suggère que Camel tire un avantage significatif de la publicité en capturant une part de marché plus importante, tandis que Marlboro souffre d'une baisse de visibilité et de ventes.
- Si Camel choisit de ne pas faire de publicité mais que Marlboro fait de la publicité, Camel gagne 2 milliards de dollars et Marlboro 5 milliards de dollars. Dans ce cas, Marlboro bénéficie de l'avantage de la publicité.
- Si ni Camel ni Marlboro ne font de la publicité, Camel gagne 4 milliards de dollars et Marlboro 4 milliards de dollars également. Cela peut refléter une situation où les deux entreprises bénéficient de coûts inférieurs en n'engageant pas de dépenses publicitaires, tout en maintenant une certaine parité dans la part de marché.
L'analyse de cette matrice de payoff montre que la publicité est une stratégie dominante pour les deux entreprises. Peu importe ce que fait l'autre entreprise, chaque entreprise a un meilleur profit en faisant de la publicité. Par conséquent, l'équilibre de Nash dans ce jeu est pour les deux entreprises de choisir de faire de la publicité, car c'est la meilleure stratégie pour chacune d'elles indépendamment de la stratégie de l'autre.
Cependant, ce n'est pas l'optimum de Pareto car les deux entreprises pourraient potentiellement gagner plus (4 milliards chacune) si aucune des deux ne faisait de publicité. Cet exemple illustre comment, même si une certaine stratégie (comme ne pas faire de publicité) pourrait être meilleure collectivement, les incitations individuelles à agir autrement conduisent à un résultat sous-optimal. Cela reflète la nature compétitive de la publicité où les entreprises sont souvent contraintes d'engager des dépenses importantes pour rester pertinentes et compétitives, même si cela réduit leurs profits globaux.
Un jeu de ressources communes[modifier | modifier le wikicode]
L'image ci-dessous représente une matrice de payoff pour un jeu de ressources communes entre deux compagnies pétrolières, BP et Shell. Chaque compagnie doit décider entre creuser un ou deux puits pétroliers. Les profits résultant de chaque combinaison de décisions sont exprimés en millions d'euros.
Si BP et Shell décident tous les deux de creuser deux puits, ils gagnent chacun 4 millions d'euros. Cette situation peut refléter une sur-exploitation de la ressource partagée, où l'augmentation de la production entraîne une baisse des prix du pétrole ou une épuisement plus rapide de la ressource, ce qui réduit les profits pour les deux compagnies.
Lorsque BP choisit de creuser deux puits tandis que Shell n'en creuse qu'un, BP gagne moins (3 millions d'euros) par rapport à Shell qui en gagne 6. Cette asymétrie peut survenir parce que Shell, en limitant sa production, bénéficie de prix plus élevés ou conserve ses ressources pour l'avenir, tandis que BP, en augmentant sa production, pourrait subir une baisse des prix due à une offre excédentaire.
Inversement, si BP décide de creuser un seul puits et que Shell en creuse deux, BP gagne 5 millions d'euros et Shell seulement 6 millions d'euros. Dans ce cas, Shell ne tire pas un avantage proportionnel à son investissement accru par rapport à BP, ce qui peut refléter une saturation du marché ou des coûts d'extraction croissants.
Si les deux compagnies choisissent de creuser un seul puits, Shell gagne 5 millions d'euros et BP gagne 6 millions d'euros. Cette situation peut indiquer que la modération dans l'exploitation des ressources conduit à de meilleurs prix du pétrole ou à une gestion plus durable des ressources, augmentant ainsi les profits.
Dans ce jeu, il n'y a pas de stratégie dominante pour les deux joueurs. Le choix de la meilleure stratégie dépend de la décision de l'autre compagnie. Si BP suppose que Shell va creuser deux puits, BP maximise ses profits en creusant seulement un puits. Si BP pense que Shell va creuser un seul puit, BP aurait intérêt à creuser deux puits. La même logique s'applique à Shell.
L'équilibre de Nash de ce jeu est moins évident. Si les deux compagnies raisonnent strictement selon les payoffs, elles pourraient finir par creuser un seul puit chacune, ce qui n'est pas le résultat le moins profitable pour aucune des deux parties. Cependant, si l'une des entreprises s'attend à ce que l'autre se modère, elle pourrait être tentée de creuser deux puits pour maximiser ses profits immédiats, ce qui pourrait conduire à une sur-exploitation. Cette situation reflète un "dilemme des communs", où les acteurs individuels profitent de la sur-utilisation d'une ressource partagée, ce qui peut mener à une épuisement à long terme de cette ressource au détriment de tous.
Le jeu oligopolistique UN et DEUX[modifier | modifier le wikicode]
L'image ci-dessous représente une matrice de payoff pour un jeu oligopolistique entre deux producteurs, UN et DEUX, qui doivent décider de la quantité de produit à vendre, soit 30 litres ou 40 litres. Les gains associés à chaque décision dépendent de l'action prise par l'autre producteur.
Si UN et DEUX choisissent tous deux de vendre 40 litres, ils gagnent chacun 1 600 euros. Cela peut indiquer une situation de concurrence où l'augmentation de l'offre a entraîné une baisse des prix, ce qui diminue les profits des deux producteurs.
Lorsque UN choisit de vendre 40 litres tandis que DEUX vend 30 litres, UN gagne 1 600 euros et DEUX gagne 2 000 euros. Inversement, si UN vend 30 litres et DEUX vend 40 litres, UN gagne 2 000 euros tandis que DEUX gagne 1 500 euros. Ces scénarios montrent qu'un producteur peut bénéficier de gains plus élevés en vendant moins si son concurrent inonde le marché avec une quantité plus importante, probablement à cause d'une meilleure tarification due à une offre plus limitée.
Si les deux producteurs décident de vendre 30 litres chacun, UN gagne 1 800 euros et DEUX gagne 1 800 euros également. Cette décision reflète probablement une entente tacite ou une coopération où les deux producteurs réduisent leur offre pour maintenir des prix plus élevés et maximiser leurs profits.
L'équilibre de non-coopération, basé sur la matrice de payoff, est atteint lorsque les deux producteurs choisissent de vendre 40 litres, car vendre 40 litres est une stratégie dominante pour chacun d'eux. C'est le résultat naturel en l'absence de coopération, car chaque producteur réagit aux actions de l'autre en maximisant son propre profit sans considération pour le profit collectif.
L'optimum pour les producteurs, qui maximiserait leur profit total, serait de coopérer et de choisir de vendre 30 litres chacun. Cela nécessiterait une certaine forme de communication ou d'accord pour limiter la production, ce qui pourrait ne pas être légal dans certains marchés réglementés en raison des lois antitrust et de concurrence.
Ce jeu illustre le défi central des oligopoles : trouver un équilibre entre les incitations individuelles à augmenter la production pour maximiser les profits individuels et les avantages potentiels d'une action collective qui pourrait conduire à de meilleurs résultats pour tous les producteurs. Sans coopération, les producteurs se retrouvent dans un équilibre de Nash non coopératif, qui n'est pas l'optimum de Pareto car ils pourraient tous deux être mieux lotis s'ils limitaient leur production. Cet équilibre reflète également le dilemme du prisonnier, où les joueurs ne parviennent pas à atteindre un accord mutuellement avantageux en raison des incitations à agir de manière indépendante.
La coopération dans un cadre dynamique[modifier | modifier le wikicode]
Dans un contexte dynamique où les jeux se répètent sur une longue période, la coopération entre les duopolistes peut devenir une stratégie plus stable et potentiellement plus profitable que la compétition agressive. Ce phénomène est souvent analysé dans le cadre des jeux répétés, aussi connus sous le nom de jeux itératifs ou supergames.
Lorsque les firmes prennent en compte les profits futurs et non pas seulement les gains immédiats, elles peuvent reconnaître qu'une stratégie de coopération à long terme maximisera leurs profits globaux. Dans cette perspective, même si une entreprise peut obtenir un gain ponctuel en trichant et en rompant l'accord de coopération, elle pourrait perdre beaucoup plus en profits futurs si l'autre entreprise répond en revenant à un comportement non coopératif.
La menace d'une punition crédible joue un rôle clé dans la stabilité de la coopération. Si UN décide de tricher, DEUX peut "punir" UN en cessant la coopération et en revenant à la compétition, ce qui réduit les profits pour les deux firmes. Pour que cette punition soit crédible, DEUX doit être prête et capable de renoncer à ses gains à court terme pour maintenir la discipline à long terme. Si cette punition est crédible et si les entreprises anticipent correctement les conséquences à long terme de leurs actions, alors la coopération peut se maintenir.
La répétition du jeu sans une date de fin connue ou dans un contexte d'incertitude quant à la durée de l'interaction peut renforcer la coopération. Si les entreprises ne savent pas quand le jeu se terminera, elles ont moins d'incitations à tricher, car elles ne peuvent pas être sûres que le gain à court terme vaudra le coût des profits perdus à l'avenir.
La théorie des jeux répétés suggère que les stratégies de coopération peuvent être soutenues par le "shadow of the future" ou l'ombre du futur. Plus le futur influence les décisions présentes, plus il est probable que les entreprises adopteront des stratégies qui favorisent la coopération. Les entreprises peuvent donc développer des mécanismes de coopération tels que des accords tacites, des stratégies de réciprocité ou des contrats à long terme pour stabiliser cette coopération et maximiser leurs profits collectifs sur le long terme.
L'oligopole et le rôle de l'État[modifier | modifier le wikicode]
L'oligopole et le rôle de l'État[modifier | modifier le wikicode]
Dans le contexte économique d'un oligopole, la coopération entre les entreprises pour fixer les prix ou limiter la production peut être bénéfique pour ces entreprises, car elle leur permet d'augmenter leurs profits en exerçant un pouvoir de marché similaire à celui d'un monopole. Cependant, cette coopération peut être préjudiciable aux consommateurs et à la société dans son ensemble, car elle peut entraîner des prix artificiellement élevés et une production inférieure à celle qui serait réalisée dans un marché plus concurrentiel. Cela peut conduire à une allocation inefficace des ressources, à une innovation moindre et à des choix réduits pour les consommateurs.
Pour cette raison, de nombreux gouvernements ont mis en place des lois antitrust ou de la concurrence pour réguler les comportements des entreprises dans les marchés oligopolistiques. Ces lois visent à prévenir les pratiques anticoncurrentielles telles que les cartels, les ententes sur les prix, les pratiques monopolistiques et les abus de position dominante. Le but est de protéger les intérêts des consommateurs, de promouvoir l'innovation et d'assurer une concurrence équitable sur le marché.
Cependant, l'approche réglementaire peut varier d'un pays à l'autre. Certains pays ont des lois antitrust très strictes et des organismes de réglementation actifs qui surveillent de près les marchés et sanctionnent les comportements anticoncurrentiels. D'autres pays peuvent avoir une approche plus souple, soit en raison de différences dans la philosophie économique, soit en raison de capacités de réglementation et de mise en œuvre plus faibles.
Les économistes ne s'accordent pas toujours sur le degré et la forme de la régulation qui devraient être appliqués. Certains plaident pour des marchés plus libres, arguant que la réglementation peut être lourde et entraver l'efficacité du marché. D'autres soutiennent que sans réglementation, les consommateurs peuvent être exploités par des entreprises puissantes. Les économistes peuvent également être en désaccord sur les effets des oligopoles sur l'innovation - certains suggèrent que les profits élevés dans les oligopoles peuvent financer la recherche et le développement, tandis que d'autres pensent que la concurrence est un meilleur stimulant pour l'innovation.
Le rôle de l'État dans la régulation des oligopoles est donc crucial et complexe. Il doit équilibrer la protection des consommateurs et la promotion de la concurrence avec la reconnaissance des réalités économiques des industries où les économies d'échelle ou les exigences de capital rendent le nombre d'acteurs naturellement limité. Cela implique souvent un ajustement constant des politiques et des réglementations pour s'adapter aux changements du marché et aux nouvelles informations.
États-Unis : le Sherman Antitrust Act[modifier | modifier le wikicode]
Le Sherman Antitrust Act est une législation fondamentale aux États-Unis qui a établi les bases de la réglementation antitrust moderne. Adoptée en 1890, cette loi visait à lutter contre les pratiques anticoncurrentielles et à démanteler les monopoles, ce qui était un problème croissant à l'époque de l'ère industrielle, notamment avec l'ascension de compagnies comme la Standard Oil de John D. Rockefeller.
Le Sherman Act est particulièrement remarquable pour deux de ses dispositions principales :
- Section 1 : Cette section interdit les accords anticoncurrentiels entre entreprises, y compris les cartels, les ententes sur les prix et d'autres formes de collusion qui restreignent le commerce.
- Section 2 : Elle cible les comportements monopolistiques, interdisant les situations où une entreprise monopolise ou tente de monopoliser un marché.
Le passage cité indique clairement que toute forme d'accord ou de complot visant à restreindre le commerce est illégal et que les individus ou entreprises coupables de tels actes seront considérés comme des criminels, passibles de lourdes amendes et/ou de peines de prison.
Le Clayton Act, qui a été adopté en 1914, a complété le Sherman Act en abordant des questions plus spécifiques et en ciblant certaines pratiques qui n'étaient pas explicitement interdites par le Sherman Act. Par exemple, le Clayton Act a mis l'accent sur des problèmes tels que la discrimination par les prix, les accords d'exclusivité et les acquisitions d'actions qui pourraient réduire la concurrence.
Ces lois sont des éléments clés de la politique de concurrence américaine et continuent d'influencer la manière dont les affaires sont menées non seulement aux États-Unis mais aussi dans les interactions commerciales internationales. L'application de ces lois est assurée par le Department of Justice des États-Unis ainsi que par la Federal Trade Commission (FTC), qui ont le pouvoir de poursuivre les entreprises pour pratiques anticoncurrentielles et de demander aux tribunaux de prendre des mesures telles que la dissolution de trusts, l'imposition d'amendes ou l'interdiction de certaines transactions commerciales. Ces lois ont joué un rôle déterminant dans la préservation de la concurrence sur les marchés américains et sont considérées comme un modèle pour les réglementations antitrust dans d'autres juridictions.
Europe : le Traité de Rome (art. 82)[modifier | modifier le wikicode]
Le Traité de Rome, signé en 1957, a établi la Communauté économique européenne (CEE), qui est maintenant intégrée dans l'Union européenne (UE). L'article 82 correspond aujourd'hui à l'article 102 du Traité sur le fonctionnement de l'Union européenne (TFUE), traite de l'abus de position dominante et est un pilier de la politique de concurrence de l'UE.
Cet article vise à empêcher les entreprises qui détiennent une position dominante sur le marché unique européen de s'engager dans des pratiques qui pourraient nuire à la concurrence et aux consommateurs. La position dominante en elle-même n'est pas interdite par le droit de l'UE, mais l'exploitation abusive de cette position l'est. Les pratiques abusives peuvent inclure :
- Imposer des prix ou des conditions de transaction non équitables : Cela peut inclure des prix excessivement élevés ou des conditions commerciales qui placent les partenaires commerciaux ou les consommateurs dans une position désavantageuse.
- Limiter la production ou le développement technique : Cela peut viser à réduire l'offre sur le marché pour maintenir les prix élevés ou à freiner l'innovation qui pourrait être bénéfique pour les consommateurs.
- Appliquer des conditions inégales à des prestations équivalentes : Cela peut entraîner une discrimination entre les partenaires commerciaux, faussant la concurrence.
- Subordonner la conclusion de contrats : Cela peut impliquer d'obliger un partenaire commercial à accepter des obligations supplémentaires qui ne sont pas liées au contrat principal, une pratique connue sous le nom de vente liée.
L'article 102 du TFUE est appliqué par la Commission européenne, qui a le pouvoir d'enquêter et de sanctionner les entreprises pour de telles pratiques. Les sanctions peuvent inclure des amendes substantielles et des ordonnances qui exigent des changements dans les pratiques commerciales des entreprises.
La politique de concurrence de l'UE, y compris l'article 102, est cruciale pour assurer un marché équitable et efficace, encourager l'innovation et protéger les consommateurs. Elle reflète l'engagement de l'UE envers une économie de marché ouverte où la concurrence est libre mais réglementée pour empêcher les abus.
Suisse : la nouvelle LCart[modifier | modifier le wikicode]
La loi fédérale sur les cartels et autres restrictions à la concurrence de la Suisse, connue sous le nom de LCart (Loi sur les Cartels), constitue le cadre juridique qui régit la concurrence dans le pays. Contrairement à l'approche de l'Union européenne qui se fonde principalement sur l'interdiction des accords anti-concurrentiels, la LCart suisse se concentre sur la notion d'abus de position dominante. Cela signifie que les accords qui pourraient limiter la concurrence ne sont pas automatiquement illicites en Suisse, à moins qu'il soit démontré qu'ils ont un effet abusif sur le marché.
La révision de 2004 a renforcé l'efficacité de la loi en permettant à la Commission de la Concurrence (Comco) d'imposer des sanctions dès la première infraction. Avant cette révision, des sanctions pouvaient seulement être infligées en cas de récidive. Ce changement montre une volonté d'appliquer la loi de manière plus stricte et de décourager les pratiques anti-concurrentielles dès la première infraction.
La LCart prévoit également un programme de clémence, aligné sur les pratiques dans d'autres juridictions comme l'UE et les États-Unis, qui vise à encourager les entreprises à collaborer avec les autorités. Ce programme permet aux entreprises qui divulguent volontairement leur participation à un cartel et qui coopèrent avec la Comco dans son enquête de bénéficier d'une réduction des amendes qui leur sont imposées. Ce mécanisme incitatif est conçu pour démanteler les cartels en incitant les membres à divulguer des informations, ce qui peut souvent être difficile à obtenir autrement pour les autorités de régulation.
Les sanctions prévues par la LCart sont significatives, avec des amendes pouvant atteindre jusqu'à 10% du chiffre d'affaires réalisé en Suisse pendant les trois dernières années. Cela donne à la loi un poids considérable et assure que les entreprises opérant en Suisse prennent sérieusement leurs obligations de conformité en matière de concurrence.
La LCart et la Comco jouent un rôle clé dans la promotion d'une concurrence équitable en Suisse, en cherchant à prévenir les pratiques qui pourraient nuire aux consommateurs et à l'économie suisse dans son ensemble. La loi est un élément essentiel pour maintenir un marché dynamique et compétitif, en assurant que les entreprises agissent de manière équitable et en prévenant les distorsions de marché.
LCart: l'abus de position dominante[modifier | modifier le wikicode]
La section de la Loi sur les Cartels (LCart) sur l'abus de position dominante spécifie les pratiques qui sont considérées comme un abus de position dominante sur le marché suisse. Ces pratiques sont interdites car elles peuvent fausser la concurrence et nuire aux consommateurs en limitant le choix ou en augmentant les prix. Voici une explication de chaque pratique illicite :
- Refus d'entretenir des relations commerciales : Cela peut inclure le refus de vendre à ou d'acheter de certains partenaires commerciaux sans justification objective. C'est souvent appelé un "refus de traiter" et peut être utilisé pour exclure des concurrents du marché ou pour punir des partenaires commerciaux pour avoir traité avec des concurrents.
- Discrimination de partenaires commerciaux : Traiter différemment les partenaires commerciaux dans des situations similaires, en particulier en matière de prix ou de conditions commerciales, peut être considéré comme discriminatoire et anticoncurrentiel.
- Imposer des prix ou conditions commerciales inéquitables : Ceci peut se référer à des prix excessivement élevés, des conditions de paiement onéreuses, ou d'autres termes qui mettent une partie à un désavantage injuste.
- Sous-enchère ciblée : Vendre à un prix inférieur au coût dans le but de saper un concurrent spécifique, avec l'intention de l'éliminer du marché, est une pratique anticoncurrentielle connue sous le nom de prédation.
- Limitation de la production, des débouchés ou du développement technique : Cela inclut les actions qui limitent artificiellement l'offre, réduisent les opportunités de vente pour les concurrents ou entravent l'innovation et le progrès technique, souvent pour maintenir des prix élevés.
- Vente liée ou conditionnement : Forcer les partenaires commerciaux à accepter des biens ou services supplémentaires qui ne sont pas liés à l'accord principal peut restreindre la concurrence et créer des barrières à l'entrée.
La LCart, en spécifiant ces pratiques comme illicites, cherche à créer un environnement de marché où la concurrence est basée sur le mérite et la performance, plutôt que sur des stratégies anticoncurrentielles. Les entreprises en position dominante doivent donc agir de manière responsable pour ne pas abuser de leur position et fausser le marché à leur avantage. Cela est crucial pour assurer une concurrence loyale et pour protéger les consommateurs ainsi que les petites et moyennes entreprises qui pourraient autrement être évincées du marché.
Résumé[modifier | modifier le wikicode]
Les marchés oligopolistiques sont caractérisés par un petit nombre d'acteurs économiques, chacun possédant une part significative du marché, ce qui leur confère un pouvoir de marché considérable. Dans un tel contexte, ces firmes ont la capacité de maximiser leurs profits collectifs en agissant conjointement à la manière d'un monopole, c'est-à-dire en formant un cartel. Cependant, l'alignement des stratégies de production individuelles sur l'objectif commun de maximisation du profit est souvent instable, comme le révèle le modèle du dilemme du prisonnier. Ce dernier met en lumière le paradoxe où les entreprises, bien que bénéficiant d'une coopération pour maintenir des prix élevés et des productions limitées, sont individuellement incitées à produire davantage pour accroître leurs parts de marché, ce qui conduit à une baisse des prix et à une augmentation de la production globale, réduisant ainsi les profits du cartel.
Par exemple, dans le cas des accords sur les quotas de production pétrolière entre les pays membres de l'OPEP, chaque pays pourrait augmenter unilatéralement sa production pour gagner plus de revenus à court terme, mais si tous les pays faisaient de même, cela entraînerait une surproduction et une chute des prix du pétrole, nuisant à tous les membres à long terme.
Lorsque le nombre de firmes dans un oligopole augmente, le marché se rapproche du modèle de la concurrence parfaite, où aucun acteur n'a suffisamment de pouvoir pour influencer les prix, résultant en des prix plus bas et des quantités produites qui tendent vers l'optimum social.
Pour prévenir les conséquences négatives des oligopoles et protéger les intérêts des consommateurs, les gouvernements ont établi des réglementations antitrust. Aux États-Unis, le Sherman Antitrust Act de 1890 a été un pas décisif pour contrer les monopoles, comme l'illustre le démantèlement de la Standard Oil de Rockefeller. De manière similaire, le Traité de Rome a posé les fondements de la politique de concurrence en Europe en interdisant l'exploitation abusive d'une position dominante sur le marché, une position qui a été renforcée par des lois telles que l'article 102 du TFUE. En Suisse, la Loi sur les Cartels met l'accent sur l'interdiction des abus de position dominante plutôt que sur l'interdiction des cartels en eux-mêmes, avec des mécanismes comme le programme de clémence pour encourager la collaboration des entreprises en cas d'enquête antitrust.
Ces lois et réglementations ne sont pas statiques ; elles évoluent avec le temps pour s'adapter aux nouvelles dynamiques économiques et aux défis posés par les pratiques commerciales en constante évolution. L'objectif reste cependant le même : maintenir des marchés justes et compétitifs, encourager l'innovation et assurer que les consommateurs bénéficient de prix équitables et de choix diversifiés.
La table fournie présente un comparatif des caractéristiques principales de quatre types de structures de marché : monopole, oligopole, concurrence monopolistique et concurrence pure et parfaite. Chacune de ces structures est définie par des critères spécifiques concernant la maximisation des profits, le pouvoir de fixation des prix, la puissance sur le marché, les conditions d'entrée, le nombre de firmes, les profits à long terme, la dépendance stratégique, la différenciation des produits et des exemples concrets.
Dans un monopole, une seule entreprise (le monopoleur) est présente sur le marché. Cette entreprise est le seul producteur d'un bien ou d'un service, lui donnant un contrôle total sur les prix – elle est un « price setter ». Le pouvoir de marché, c'est-à-dire la capacité de fixer les prix au-dessus du coût marginal (MC), est maximal dans un monopole. Les conditions d'entrée sont telles qu'aucune autre entreprise ne peut entrer sur le marché, souvent à cause de barrières légales ou naturelles. Un monopole peut faire des profits à long terme (≥ 0), car il n'y a pas de pression concurrentielle qui forcerait les prix à baisser jusqu'au niveau du coût marginal. Les produits peuvent être différenciés, comme dans le cas d'une compagnie de gaz naturel locale, qui pourrait être l'unique fournisseur pour une région donnée.
En contraste, un oligopole se compose de quelques entreprises qui dominent un marché. Chacune possède une part significative du marché, ce qui leur confère un pouvoir de marché et leur permet de fixer des prix au-dessus du coût marginal. L'entrée sur le marché est limitée, mais pas impossible, ce qui signifie que les barrières à l'entrée sont significatives mais pas insurmontables. Les firmes oligopolistiques peuvent maintenir des profits à long terme grâce à leur puissance sur le marché. Les stratégies sont interdépendantes : les décisions d'une entreprise affectent et sont affectées par les décisions des concurrents. Les produits en oligopole peuvent être différenciés, comme dans le cas des fabricants d'automobiles, où les marques se concurrencent sur des bases telles que la qualité, le style et la réputation.
La concurrence monopolistique est un terme moyen entre l'oligopole et la concurrence parfaite. Les marchés présentent un grand nombre de firmes, et l'entrée est libre, ce qui signifie que les barrières à l'entrée sont faibles ou inexistantes. Les entreprises peuvent fixer des prix, mais leur pouvoir de marché est limité en raison de la présence de nombreux concurrents proches. Elles peuvent obtenir des profits à court terme, mais à long terme, la concurrence entraîne une érosion des profits (tendant vers zéro). La différenciation des produits est une caractéristique clé de la concurrence monopolistique, permettant aux entreprises de gagner des clients fidèles malgré la présence de nombreux substituts proches. Un exemple classique pourrait être celui des plombiers dans une petite ville, où chacun offre un service légèrement différent.
Enfin, la concurrence pure et parfaite représente un idéal théorique où de nombreuses firmes produisent des biens homogènes. Les entreprises sont des « price takers », ce qui signifie qu'elles n'ont aucun pouvoir de fixation des prix et doivent accepter le prix du marché déterminé par l'offre et la demande globales. L'entrée sur le marché est libre, il y a beaucoup d'entreprises, et les profits à long terme sont nuls en raison de la concurrence intense. Les produits sont indifférenciés, ou "commodités", comme dans le cas des agriculteurs produisant des pommes, où les pommes d'un producteur sont considérées comme équivalentes à celles d'un autre.
Chacune de ces structures de marché a des implications distinctes pour les consommateurs, les entreprises et la politique économique. Par exemple, les monopoles peuvent nécessiter une réglementation pour empêcher l'abus de pouvoir de marché, tandis que les marchés concurrentiels peuvent fonctionner avec peu d'intervention étatique.
Annexes[modifier | modifier le wikicode]
- Universalis, Encyclopædia. “ÉQUILIBRE ÉCONOMIQUE.” Encyclopædia Universalis, www.universalis.fr/encyclopedie/equilibre-economique/10-l-equilibre-de-nash/.