« Costi di produzione » : différence entre les versions
(→Résumé) |
|||
| (8 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 85 : | Ligne 85 : | ||
Questi costi impliciti sono spesso difficili da quantificare con precisione, in quanto implicano stime su quale potrebbe essere un'alternativa "migliore". Tuttavia, sono fondamentali per le decisioni economiche perché forniscono una misura più realistica della performance economica di un'azienda. Ignorare i costi impliciti potrebbe portare a una valutazione eccessiva della salute e del successo finanziario dell'azienda, in quanto il profitto contabile potrebbe apparire più alto del profitto economico effettivo dopo aver tenuto conto di questi costi. In breve, i costi impliciti svolgono un ruolo fondamentale nel prendere decisioni economiche consapevoli. Aiutano a valutare se le risorse dell'azienda sono utilizzate nel modo più vantaggioso possibile e se l'azienda sta generando un rendimento sufficiente a giustificare questi costi opportunità. | Questi costi impliciti sono spesso difficili da quantificare con precisione, in quanto implicano stime su quale potrebbe essere un'alternativa "migliore". Tuttavia, sono fondamentali per le decisioni economiche perché forniscono una misura più realistica della performance economica di un'azienda. Ignorare i costi impliciti potrebbe portare a una valutazione eccessiva della salute e del successo finanziario dell'azienda, in quanto il profitto contabile potrebbe apparire più alto del profitto economico effettivo dopo aver tenuto conto di questi costi. In breve, i costi impliciti svolgono un ruolo fondamentale nel prendere decisioni economiche consapevoli. Aiutano a valutare se le risorse dell'azienda sono utilizzate nel modo più vantaggioso possibile e se l'azienda sta generando un rendimento sufficiente a giustificare questi costi opportunità. | ||
=== Analisi del commercialista e dell'economista nella valutazione dei costi e dei profitti di un'azienda == | === Analisi del commercialista e dell'economista nella valutazione dei costi e dei profitti di un'azienda === | ||
Il ruolo del commercialista e dell'economista nella valutazione dei costi e dei profitti di un'azienda differisce in modo significativo a causa dei rispettivi approcci ai costi impliciti. | Il ruolo del commercialista e dell'economista nella valutazione dei costi e dei profitti di un'azienda differisce in modo significativo a causa dei rispettivi approcci ai costi impliciti. | ||
| Ligne 95 : | Ligne 95 : | ||
Questa distinzione è fondamentale perché può portare a interpretazioni molto diverse della performance finanziaria di un'azienda. Un utile contabile positivo non significa necessariamente che l'azienda sia economicamente sostenibile se, una volta presi in considerazione i costi impliciti, l'utile economico risulta essere pari a zero o negativo. Di conseguenza, le decisioni basate esclusivamente sui dati contabili possono talvolta essere fuorvianti se non si tiene conto anche dei costi opportunità delle risorse impiegate. | Questa distinzione è fondamentale perché può portare a interpretazioni molto diverse della performance finanziaria di un'azienda. Un utile contabile positivo non significa necessariamente che l'azienda sia economicamente sostenibile se, una volta presi in considerazione i costi impliciti, l'utile economico risulta essere pari a zero o negativo. Di conseguenza, le decisioni basate esclusivamente sui dati contabili possono talvolta essere fuorvianti se non si tiene conto anche dei costi opportunità delle risorse impiegate. | ||
== Utile economico e utile contabile | == Utile economico e utile contabile == | ||
La distinzione tra utile economico e utile contabile è fondamentale per l'analisi della performance di un'azienda. | La distinzione tra utile economico e utile contabile è fondamentale per l'analisi della performance di un'azienda. | ||
| Ligne 141 : | Ligne 141 : | ||
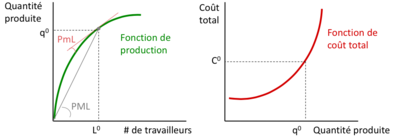
L'analisi di questi grafici è fondamentale per la gestione aziendale. La funzione di produzione mostra come l'efficienza del lavoro influenzi la quantità di beni o servizi che possono essere prodotti, mentre la funzione di costo totale mostra come questi livelli di produzione si traducano in costi. La comprensione di queste relazioni aiuta le aziende a ottimizzare i livelli di produzione per massimizzare i profitti. Ad esempio, un'azienda potrebbe cercare di produrre a un livello in cui la produttività marginale sia elevata prima che i rendimenti decrescenti inizino a manifestarsi, monitorando al contempo i costi totali per garantire che i costi variabili non inizino a crescere in modo sproporzionato rispetto alla produzione. | L'analisi di questi grafici è fondamentale per la gestione aziendale. La funzione di produzione mostra come l'efficienza del lavoro influenzi la quantità di beni o servizi che possono essere prodotti, mentre la funzione di costo totale mostra come questi livelli di produzione si traducano in costi. La comprensione di queste relazioni aiuta le aziende a ottimizzare i livelli di produzione per massimizzare i profitti. Ad esempio, un'azienda potrebbe cercare di produrre a un livello in cui la produttività marginale sia elevata prima che i rendimenti decrescenti inizino a manifestarsi, monitorando al contempo i costi totali per garantire che i costi variabili non inizino a crescere in modo sproporzionato rispetto alla produzione. | ||
== | == Prodotto marginale e medio del lavoro == | ||
Il prodotto marginale del lavoro (MPL) è un concetto fondamentale in economia che descrive l'impatto aggiuntivo sulla produzione totale dell'aggiunta di un lavoratore in più, assumendo che tutti gli altri fattori di produzione rimangano costanti. È una misura dell'efficienza marginale del lavoro nel processo produttivo. | |||
Matematicamente, per piccoli incrementi, il prodotto marginale del lavoro può essere espresso come il rapporto tra la variazione della quantità prodotta (<math>Delta q</math>) e la variazione della manodopera (<math>Delta L</math>), ottenendo la formula: | |||
<math>PmL = \frac{\Delta q}{\Delta L}</math> | <math>PmL = \frac{\Delta q}{\Delta L}</math> | ||
Questa formula rappresenta il tasso di variazione della produzione rispetto alla variazione della quantità di lavoro utilizzata, ovvero la pendenza della funzione di produzione sul grafico. In un'analisi più dettagliata e precisa, soprattutto quando siamo interessati a variazioni infinitesimali, il prodotto marginale del lavoro è rappresentato dalla derivata parziale della quantità prodotta rispetto al lavoro, nota come : | |||
<math>PmL = \frac{\partial q}{\partial L}</math> | <math>PmL = \frac{\partial q}{\partial L}</math> | ||
Questa derivata parziale fornisce l'esatta pendenza della funzione di produzione in un determinato punto e riflette l'aumento della produzione derivante dall'aggiunta di un'unità infinitesimale di lavoro. | |||
Il concetto di prodotto marginale è fondamentale per capire come le aziende decidono la quantità di lavoro da impiegare. In teoria, un'impresa aumenta la quantità di lavoro fino al punto in cui il prodotto marginale del lavoro è uguale al salario reale, cioè al costo di questa unità di lavoro aggiuntiva. A questo punto, l'impresa massimizza il proprio profitto, perché l'assunzione di un lavoratore in più non produrrebbe una produzione aggiuntiva sufficiente a coprire il costo del suo salario. | |||
In pratica, l'impresa cerca il livello di produzione in cui il costo marginale di produzione (che include il prodotto marginale del lavoro) è uguale al ricavo marginale, al fine di massimizzare i profitti. Tuttavia, vari fattori come i cambiamenti tecnologici, gli aggiustamenti del mercato del lavoro e le normative possono influenzare il prodotto marginale del lavoro e, di conseguenza, la strategia ottimale dell'impresa in materia di lavoro. | |||
La | La funzione di produzione illustrata suggerisce che il prodotto marginale del lavoro (MPL) è decrescente, il che implica che l'aggiunta di lavoratori supplementari aumenta la produzione, ma in proporzioni sempre minori. Si tratta di una manifestazione del principio dei rendimenti decrescenti, secondo il quale l'efficienza di ogni lavoratore aggiuntivo diminuisce all'aumentare della quantità di lavoro, mantenendo costanti gli altri fattori di produzione. | ||
In termini matematici, ciò significa che la derivata prima della funzione di produzione rispetto al lavoro, <math>frac {parziale q}{parziale L}</math>, diminuisce all'aumentare di L. Graficamente, la pendenza della curva di produzione, che rappresenta l'AMP, diminuisce man mano che ci si sposta lungo la curva verso destra, indicando che ogni lavoratore aggiuntivo contribuisce meno alla produzione totale rispetto al lavoratore precedente. | |||
Il prodotto medio del lavoro (ALP), invece, è una misura diversa che indica la produzione media per lavoratore. Si calcola dividendo la produzione totale (q) per il numero totale di lavoratori (L), dato dalla formula <math>frac {q}{L}</math>. Su un grafico della funzione di produzione, il PML è rappresentato dalla pendenza di una semiretta che parte dall'origine e arriva a un punto specifico della curva di produzione. Questo raggio indica la produzione media per tutti i livelli di manodopera impiegati fino a quel punto. | |||
Quando il numero di lavoratori è basso, il LMP può aumentare con l'assunzione di altri lavoratori, che contribuiscono in modo significativo all'aumento della produzione. Tuttavia, in presenza di rendimenti decrescenti, si arriverà a un punto in cui l'aggiunta di nuovi lavoratori inizierà a far diminuire il LMP, perché l'aumento totale della produzione sarà inferiore all'aumento del numero di lavoratori. Questo accade quando il PML è inferiore al PML. | |||
La | La comprensione di questi indicatori è fondamentale per le aziende quando decidono di assumere nuovi lavoratori. Le aziende cercheranno di bilanciare il costo dell'aggiunta di lavoratori con i benefici della produzione aggiuntiva per massimizzare l'efficienza e la redditività. | ||
== | == Rendimenti decrescenti == | ||
La | La legge dei rendimenti marginali decrescenti è un principio fondamentale dell'economia che descrive come, dopo un certo punto, ogni unità aggiuntiva di un fattore di produzione (in questo caso, il lavoro) contribuisca meno alla produzione totale rispetto alla precedente, quando tutti gli altri fattori di produzione sono mantenuti costanti. Si tratta di una legge che ha importanti implicazioni per la produttività e le decisioni sulla produzione. | ||
L' | L'intuizione alla base di questa legge può essere compresa con un semplice esempio: immaginate una cucina con un unico forno e diversi cuochi. Inizialmente, l'aggiunta di altri cuochi può aumentare la produzione di pasti perché c'è abbastanza lavoro per tutti e il forno viene utilizzato in modo ottimale. Tuttavia, una volta raggiunto il numero ottimale di cuochi in cucina, l'aggiunta di altro personale non renderà più veloce la cottura dei pasti perché il forno diventa un collo di bottiglia. I cuochi in più potrebbero addirittura ostacolarsi a vicenda, con una conseguente riduzione dell'efficienza complessiva. | ||
Applicato al contesto più ampio della produzione economica, ciò significa che se un'azienda continua ad aggiungere manodopera a una quantità fissa di altre risorse (come macchinari, edifici o tecnologia), il contributo aggiuntivo di ogni nuovo lavoratore diminuirà. I primi lavoratori possono utilizzare in modo efficiente le macchine e lo spazio a disposizione, ma i lavoratori successivi avranno meno macchine da utilizzare e meno spazio in cui lavorare, riducendo la loro produttività marginale. | |||
Questa legge spiega perché le aziende non possono semplicemente aumentare la produzione all'infinito aggiungendo altri lavoratori. Devono invece trovare un equilibrio tra il numero di lavoratori e la quantità di altre risorse a loro disposizione. Per aumentare la produzione oltre un certo punto, un'azienda dovrà investire in altri fattori produttivi, come l'acquisto di macchinari aggiuntivi o l'ampliamento delle strutture, piuttosto che affidarsi esclusivamente all'aggiunta di manodopera. | |||
Quando i lavoratori si trovano a dover condividere risorse limitate come computer o fotocopiatrici, l'efficienza individuale inizia a diminuire. Questo calo si manifesta inizialmente con piccole inefficienze, come l'attesa per l'utilizzo delle attrezzature, ma può rapidamente degenerare in problemi più significativi di coordinamento e comunicazione quando si aggiungono altri lavoratori. I ritardi si accumulano, i lavoratori passano più tempo ad aspettare che a produrre e la frustrazione può portare a un morale basso, incidendo ulteriormente sulla produttività. | |||
Graficamente, questo si traduce in una funzione di produzione che, dopo un certo punto, si appiattisce all'aumentare della quantità di lavoro, riflettendo una diminuzione della produttività marginale. Ogni lavoratore aggiuntivo aggiunge meno alla produzione totale rispetto al lavoratore che lo ha preceduto. Il grafico della funzione di costo totale rivela l'impatto finanziario di questa legge: all'aumentare della produzione, iniziano a crescere anche i costi marginali, ossia il costo di produzione di un'unità aggiuntiva. Questo perché, se la produzione richiede più manodopera per ogni unità aggiuntiva a causa della congestione delle risorse, il costo di produzione di quell'unità aggiuntiva aumenterà inevitabilmente. | |||
In realtà, le aziende possono incontrare questo problema quando le loro dimensioni raggiungono un punto in cui le risorse iniziano a scarseggiare rispetto al numero di dipendenti. La soluzione per evitare questa trappola non è sempre quella di aggiungere altre risorse, ma può anche comportare una migliore gestione delle risorse esistenti, il miglioramento dei processi di lavoro o l'investimento in tecnologie che migliorino l'efficienza. | |||
L' | L'intuizione alla base della legge dei rendimenti marginali decrescenti e del suo impatto sui costi è che l'efficienza e la redditività possono risentirne se un'azienda non riesce a bilanciare correttamente l'uso del lavoro con le altre risorse a sua disposizione. Ciò sottolinea l'importanza della gestione strategica delle risorse per ottimizzare la produzione e controllare i costi in un determinato ambiente produttivo. | ||
== | == Caso di studio: funzione di produzione e costo totale == | ||
L' | L'esempio seguente mostra la funzione di produzione e la struttura dei costi di un produttore di pizza in funzione del numero di lavoratori impiegati. Quando la pizzeria non impiega lavoratori, naturalmente non c'è produzione e il costo totale è costituito esclusivamente dai costi fissi del negozio, che ammontano a 30. Questa somma è probabilmente rappresentativa di costi quali l'affitto, le utenze e l'ammortamento delle attrezzature. Questa somma è probabilmente rappresentativa di costi quali l'affitto, le utenze e l'ammortamento delle attrezzature, che sono invariabili indipendentemente dal livello di attività. | ||
[[Fichier:Exemple fonction de production et coût total 1.png|450px|vignette|centré| | [[Fichier:Exemple fonction de production et coût total 1.png|450px|vignette|centré|Funzione di produzione e costo totale di un produttore di pizza.]] | ||
Con l'introduzione del primo lavoratore, la produzione inizia a 50 pizze, il che indica un contributo significativo all'attività da parte di questo singolo lavoratore. Il costo totale sale modestamente a 40, incorporando il costo fisso del laboratorio più un costo variabile aggiuntivo di 10 per la manodopera. Questo costo aggiuntivo rappresenta il salario o lo stipendio del lavoratore. | |||
Con l'aggiunta di ogni altro lavoratore, la produzione di pizze aumenta, ma è interessante notare che l'aumento della produzione diminuisce ogni volta, passando da 40 pizze in più con il primo lavoratore a solo 10 pizze in più con il quarto lavoratore. Ciò illustra la legge dei rendimenti marginali decrescenti, per cui ogni lavoratore aggiuntivo contribuisce sempre meno alla produzione complessiva, probabilmente a causa della limitazione delle risorse condivise, come lo spazio di lavoro o le attrezzature della cucina. | |||
Allo stesso tempo, sebbene il costo fisso dell'officina rimanga costante, il costo totale del lavoro aumenta linearmente con l'aggiunta di ogni nuovo lavoratore. Questo aumento lineare è il risultato dell'aggiunta del costo del lavoro per ogni nuovo lavoratore, ipotizzando che ogni lavoratore costi lo stesso importo, indipendentemente dalla produzione realizzata. | |||
Infine, il costo totale di produzione, che è la somma dei costi fissi e variabili, aumenta con ogni aggiunta di lavoratori, riflettendo l'aumento dei costi di produzione. Tuttavia, dato il calo della produttività marginale, aumenta anche il costo di produzione di un'unità aggiuntiva, il che significa che l'azienda deve spendere di più per ogni pizza aggiuntiva prodotta oltre un certo punto. Ciò suggerisce che, sebbene l'aggiunta di manodopera possa aumentare la produzione, lo fa a un costo marginale crescente, un fattore che le imprese devono gestire con attenzione per mantenere la redditività. | |||
Questa analisi evidenzia l'importanza di ottimizzare il numero di lavoratori nella produzione. Un produttore di pizza, o qualsiasi azienda, deve individuare il numero ottimale di lavoratori per massimizzare la produzione senza incorrere in costi sproporzionati dovuti alla diminuzione dei rendimenti marginali. Ciò richiede un'attenta comprensione dei costi fissi e variabili e del loro impatto sul costo totale e sulla redditività dell'azienda. | |||
[[Fichier:Exemple fonction de production et coût total 2.png|450px|vignette|centré| | [[Fichier:Exemple fonction de production et coût total 2.png|450px|vignette|centré|Funzione di produzione.]] | ||
Questo grafico rappresenta la funzione di produzione che mostra la relazione tra il numero di lavoratori assunti e la quantità di pizze prodotte all'ora da un produttore di pizza. Il grafico mostra una tipica curva di produzione che inizialmente aumenta rapidamente con l'aggiunta di lavoratori, ma inizia ad appiattirsi dopo un certo numero di lavoratori assunti, indicando una diminuzione della produttività marginale. | |||
Inizialmente, con l'aggiunta dei primi lavoratori, l'aumento della produzione è sostanziale per ogni lavoratore aggiuntivo, a dimostrazione di un'elevata produttività marginale. Ciò può essere dovuto a un uso più efficiente delle attrezzature e a una specializzazione del lavoro che consente un aumento significativo della produzione. | |||
Tuttavia, il grafico mostra anche che, dopo l'aggiunta di alcuni lavoratori, la produzione continua a crescere ma a un ritmo più lento. Questo accade perché ogni lavoratore aggiuntivo contribuisce alla produzione complessiva in misura minore rispetto al precedente, un fenomeno che riflette la legge dei rendimenti marginali decrescenti. Questa legge suggerisce che esiste un punto ottimale di lavoro oltre il quale l'efficienza di ogni lavoratore aggiuntivo inizia a diminuire, spesso a causa della condivisione di risorse limitate o della congestione. | |||
Il grafico mostra che l'assunzione del quarto e del quinto lavoratore, ad esempio, aumenta la produzione ma a un tasso decrescente rispetto ai primi lavoratori. Questo può essere interpretato come un segno che lo spazio di lavoro, i forni per la pizza o altre attrezzature stanno diventando un vincolo e che l'aggiunta di altri lavoratori non può essere sfruttata appieno. | |||
Per il produttore di pizza, questo grafico è essenziale per determinare il numero ottimale di lavoratori da assumere per massimizzare la produzione senza incorrere in costi inutili per guadagni marginali di produzione. Analizzando il punto in cui la curva inizia ad appiattirsi, il produttore può identificare il punto di diminuzione dei rendimenti e prendere decisioni informate sulle dimensioni della forza lavoro da mantenere per ottenere un'efficienza ottimale. | |||
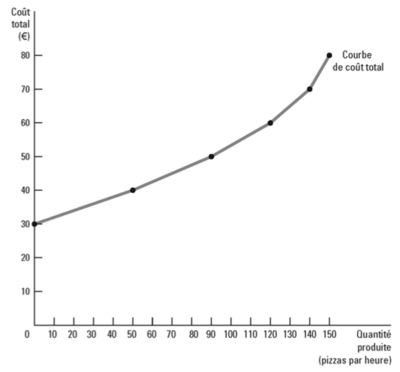
[[Fichier:Exemple fonction de production et coût total 3.png|450px|vignette|centré| | [[Fichier:Exemple fonction de production et coût total 3.png|450px|vignette|centré|Curva dei costi totali.]] | ||
La | La curva del costo totale mostrata nell'immagine rappresenta la relazione tra la quantità prodotta (pizze all'ora) e il costo totale in euro. La curva mostra una progressione verso l'alto che si intensifica all'aumentare della produzione, tipica delle funzioni di costo totale in cui i costi variano con la produzione. | ||
La | La parte iniziale della curva sale relativamente lentamente, suggerendo che i costi fissi dominano quando la produzione è bassa. I costi fissi sono spese che non cambiano con il livello di produzione, come l'affitto del negozio, il costo delle attrezzature e forse lo stipendio base dei dipendenti. Pertanto, quando il numero di pizze prodotte è basso, l'aumento del costo totale è moderato perché i costi variabili (come gli ingredienti della pizza e il costo marginale del lavoro) sono ancora minimi. | ||
Con l'aumento della produzione, la curva sale più ripidamente. Ciò indica che i costi variabili iniziano ad avere un impatto significativo sui costi totali. I costi variabili possono includere la spesa extra per gli ingredienti, l'energia utilizzata per cuocere più pizze e i salari extra per i lavoratori assunti per aumentare la produzione. Questo aspetto della curva è coerente con la legge dei rendimenti marginali decrescenti: con l'aumento della produzione, i costi marginali della produzione di ogni pizza aggiuntiva aumentano a causa dell'uso meno efficiente delle risorse, man mano che il negozio si avvicina o supera la sua capacità produttiva ottimale. | |||
La | La forma della curva suggerisce che ogni pizza aggiuntiva costa di più rispetto alla precedente, indicando rendimenti di scala decrescenti in questa fascia di produzione. Questa è una considerazione importante per il produttore di pizza quando pianifica l'espansione della produzione. Se continua ad aumentare la produzione, il costo per unità continuerà a crescere, riducendo i profitti. | ||
Per massimizzare la redditività, il produttore deve trovare il livello di produzione in cui il costo totale per unità prodotta è più basso. Ciò implica il raggiungimento di un equilibrio tra costi fissi e variabili, evitando di produrre oltre il punto in cui i costi marginali iniziano a superare i ricavi marginali. La curva dei costi totali è uno strumento essenziale per identificare questo punto e prendere decisioni consapevoli sulla quantità di produzione. | |||
= | = Diverse misure di costo = | ||
== | == Diverse misure di costo == | ||
=== | === Costi fissi === | ||
I costi fissi (FC) rappresentano le spese che un'azienda deve coprire indipendentemente dalla sua produzione. Questi costi rimangono costanti in un determinato periodo anche se la quantità di beni o servizi prodotti varia. I costi fissi sono spesso associati agli investimenti in capitale fisico, come l'acquisto o il noleggio di attrezzature ed edifici, che non cambiano in base alla produzione o alle vendite dell'azienda. | |||
Nel caso di un produttore di pizza, i costi fissi potrebbero includere l'affitto di uno spazio commerciale, l'acquisto o l'ammortamento dei forni per la pizza e delle attrezzature da cucina, gli stipendi dei dipendenti garantiti indipendentemente dal numero di pizze vendute, l'assicurazione e forse alcuni servizi di pubblica utilità come l'acqua o l'abbonamento a Internet. Ad esempio, sia che il produttore di pizza faccia 10 pizze o 100 pizze, l'affitto del locale rimarrà lo stesso per il periodo in questione. Allo stesso modo, l'acquisto di un forno per pizza è un costo iniziale che non cambia, sia che il forno venga utilizzato per cuocere una sola pizza, sia che venga utilizzato in modo continuativo. | |||
È fondamentale per le imprese comprendere e gestire i costi fissi, in quanto costituiscono una parte importante della struttura dei costi totali e possono influenzare le decisioni sui prezzi, sulla strategia di produzione e sulla redditività a lungo termine. Un livello elevato di costi fissi può anche aumentare il rischio finanziario di un'azienda, poiché questi costi devono essere coperti indipendentemente dai ricavi. Le aziende devono quindi generare entrate sufficienti a coprire non solo i costi variabili, ma anche i costi fissi, per evitare perdite. | |||
=== | === Costi variabili === | ||
I costi variabili (VC) nel contesto della produzione di un'azienda sono quelli che fluttuano in base al volume dell'attività o della produzione. A differenza dei costi fissi, che rimangono costanti indipendentemente dal livello di produzione, i costi variabili cambiano direttamente con la quantità di beni o servizi prodotti. | |||
Nell'esempio di un produttore di pizza, i costi variabili comprendono gli ingredienti necessari per la preparazione delle pizze, come la farina, la salsa di pomodoro, il formaggio e i condimenti, nonché il costo dell'energia consumata per far funzionare i forni e le altre attrezzature della cucina. Inoltre, se i lavoratori sono pagati all'ora o al pezzo, anche i loro salari sono costi variabili, poiché la manodopera totale richiesta varia in base al numero di pizze prodotte. | |||
Se il produttore produce più pizze, avrà bisogno di più ingredienti e possibilmente di più ore di lavoro, il che aumenterà i suoi costi variabili. Al contrario, se decide di ridurre la produzione, i suoi costi variabili diminuiranno perché utilizzerà meno ingredienti e meno manodopera. | |||
I costi variabili sono essenziali per la gestione aziendale perché influenzano direttamente il margine di profitto per unità venduta. Una chiara comprensione dei costi variabili è necessaria per stabilire strategie di prezzo efficaci e per prendere decisioni sui livelli di produzione ottimali. Controllando e riducendo i costi variabili, un'azienda può aumentare il proprio margine su ogni prodotto venduto, il che è fondamentale per la redditività complessiva. Allo stesso modo, quando si valuta la redditività di un nuovo prodotto o servizio, un'analisi approfondita dei costi variabili associati è fondamentale per garantire che il prezzo di vendita copra tali costi e contribuisca positivamente al profitto complessivo. | |||
=== | === Costo totale === | ||
Il costo totale (TC) è la somma del costo fisso (FC) e del costo variabile (VC). Questa relazione è fondamentale per comprendere la struttura dei costi di un'azienda ed è espressa matematicamente come segue: | |||
TC = FC + VC | |||
Questa equazione illustra che per ogni livello di produzione, il costo totale è composto da una parte che non cambia, rappresentata dai costi fissi, e da una parte che fluttua con il livello di produzione, rappresentata dai costi variabili. I costi fissi sono spese che devono essere pagate indipendentemente dal volume di produzione, come l'affitto, gli stipendi dei dipendenti fissi, il pagamento dei prestiti e l'ammortamento delle attrezzature. I costi variabili variano in base alla produzione, come le materie prime, le forniture e le ore di lavoro pagate per la produzione. | |||
Ad esempio, se un produttore di pizze ha costi fissi mensili di 2.000 euro per l'affitto, le attrezzature e i salari fissi, e costi variabili di 2 euro per pizza per gli ingredienti e l'energia, il costo totale della produzione di 1.000 pizze sarà calcolato sommando il costo fisso al costo variabile totale per quella produzione: | |||
TC = CF + (CV per pizza × numero di pizze) | |||
CT = 2000 + (2 × 1000) | CT = 2000 + (2 × 1000) | ||
CT= 2000 + 2000 | CT= 2000 + 2000 | ||
TC =4000 euro | |||
La | La comprensione del costo totale è fondamentale per prendere decisioni sui prezzi e sui livelli di produzione. Conoscendo il costo totale, un'azienda può determinare il prezzo di vendita minimo necessario per coprire tutti i costi e generare un profitto. Inoltre, analizzando come varia il costo totale al variare del livello di produzione, le aziende possono identificare il punto di produzione più efficiente e massimizzare la loro redditività. | ||
=== | === Costo medio === | ||
Il costo medio (CA), noto anche come costo unitario, è una misura utilizzata per comprendere il costo di produzione per unità di bene o servizio prodotto. Si ottiene dividendo il costo totale (TC) per la quantità totale prodotta (q). Questa relazione è rappresentata dalla seguente formula: | |||
<math> CM = \frac{CT}{q} </math> | <math> CM = \frac{CT}{q} </math> | ||
Poiché il costo totale è la somma dei costi fissi e variabili, il costo medio può anche essere espresso come la somma del costo fisso medio (AFC) e del costo variabile medio (AVC), dove il costo fisso medio è il costo fisso per unità prodotta e il costo variabile medio è il costo variabile per unità prodotta. Pertanto, il costo medio è rappresentato anche dalla formula: | |||
<math> CM = \frac{CF}{q} + \frac{CV}{q} </math> | <math> CM = \frac{CF}{q} + \frac{CV}{q} </math> | ||
Ciò significa che per ogni unità prodotta viene allocata una parte del costo fisso e una parte del costo variabile. Il costo medio consente alle aziende di determinare il costo di produzione di ogni unità di prodotto, che è fondamentale per stabilire prezzi di vendita adeguati e valutare l'efficienza della produzione. | |||
Ad esempio, se un produttore di pizza ha un costo fisso di 2.000 euro e produce 1.000 pizze, il costo fisso medio per pizza è di 2 euro (2.000 euro / 1.000 pizze). Se il totale dei costi variabili per queste 1.000 pizze è di 2.000 euro, anche il costo variabile medio per pizza è di 2 euro (2.000 euro / 1.000 pizze). Il costo medio per pizza sarebbe quindi di 4 euro (2 euro MVC + 2 euro MVC), prima di prendere in considerazione il margine di profitto. | |||
La comprensione del costo medio è particolarmente importante per la strategia dei prezzi. Se il costo medio è inferiore al prezzo di vendita per unità, l'azienda realizza un profitto su ogni unità venduta. Se il costo medio è superiore al prezzo di vendita, l'azienda subisce una perdita per ogni unità. L'obiettivo è quindi spesso quello di ridurre il costo medio, tagliando i costi o aumentando la produzione per distribuire i costi fissi su un maggior numero di unità, riducendo così il costo fisso medio. | |||
=== | === Costo marginale ===== | ||
Il costo marginale (MC) svolge un ruolo cruciale nell'analisi economica della produzione, in quanto misura l'impatto sul costo totale di un'azienda della produzione di un'unità aggiuntiva di un bene o servizio. È essenzialmente la pendenza della funzione di costo totale in un determinato punto, che rappresenta l'aumento del costo totale per ogni incremento unitario della produzione. | |||
Matematicamente, il costo marginale è definito come il rapporto tra la variazione del costo totale (<math>Delta CT</math>) e la variazione della quantità prodotta (<math>Delta q</math>). La formula è la seguente: | |||
<math>Cm = \frac{\Delta CT}{\Delta q}</math> | <math>Cm = \frac{\Delta CT}{\Delta q}</math> | ||
Quando si considerano variazioni molto piccole della quantità prodotta, il costo marginale può essere espresso come la derivata del costo totale rispetto alla quantità. Per variazioni infinitesimali, la formula è : | |||
<math>Cm = \frac{\partial CT}{\partial q}</math> | <math>Cm = \frac{\partial CT}{\partial q}</math> | ||
Le | Il costo marginale è particolarmente importante nelle decisioni di produzione e di prezzo. Le aziende cercheranno di produrre fino al punto in cui il costo marginale è uguale al ricavo marginale, che è il ricavo aggiuntivo ottenuto dalla vendita di un'unità supplementare. Questo punto è fondamentale perché corrisponde al livello di produzione in cui i profitti sono massimizzati. Se il costo marginale è inferiore al prezzo di vendita dell'unità aggiuntiva, è vantaggioso per l'azienda aumentare la produzione. Al contrario, se il costo marginale supera il prezzo di vendita, produrre di più ridurrebbe il profitto dell'azienda. | ||
In pratica, l'analisi del costo marginale aiuta le aziende ad adeguare il proprio livello di produzione in risposta ai cambiamenti della domanda di mercato, alle variazioni dei costi dei fattori produttivi o all'introduzione di nuove tecnologie, con l'obiettivo di massimizzare l'efficienza e la redditività. | |||
== | == Esempio == | ||
Questa tabella illustra i costi di produzione di un produttore di limonata. Mostra la relazione tra il numero di bicchieri di limonata prodotti all'ora e i diversi tipi di costo: costo totale, costo fisso, costo variabile, nonché i relativi costi medi e marginali. | |||
[[Fichier:Exemple mesures de couts 1.png|400px|vignette|centré| | [[Fichier:Exemple mesures de couts 1.png|400px|vignette|centré|Costi di produzione per un produttore di limonata]] | ||
Il costo fisso rimane costante a 3,00 euro, suggerendo che si tratta di costi che non dipendono dal volume di produzione, come l'affitto o l'ammortamento delle attrezzature. Il costo totale parte da 3,00 euro quando non viene prodotto vetro e aumenta con la produzione. La differenza tra il costo totale in ogni fase e il costo fisso dà il costo variabile, che aumenta con il numero di bicchieri prodotti. | |||
I costi fissi medi (AFC) sono calcolati dividendo il costo fisso per il numero di lenti prodotte. Poiché il costo fisso è costante, l'AFC diminuisce all'aumentare del volume di produzione. Al contrario, il costo variabile medio (AVC) si ottiene dividendo il costo variabile totale per il numero di lenti prodotte. Il costo medio totale (TC) rappresenta la somma del MFC e dell'AVC e inizialmente diminuisce prima di aumentare leggermente, suggerendo che potrebbe esistere un intervallo di produzione ottimale in cui i costi medi sono minimizzati. | |||
Il costo marginale (MC) rappresenta il costo di un bicchiere aggiuntivo e si ottiene osservando la variazione del costo totale diviso per la variazione della quantità prodotta. Parte da 0,30 euro e aumenta progressivamente, indicando che ogni bicchiere aggiuntivo costa di più alla produzione rispetto al precedente. Ciò riflette i rendimenti marginali decrescenti, in cui il costo aggiuntivo della produzione aumenta dopo un certo punto perché, ad esempio, le attrezzature vengono utilizzate in modo eccessivo o è necessario assumere più manodopera a un tasso più elevato per mantenere la produzione. | |||
Questa serie di dati consente al produttore di limonata di comprendere la propria struttura dei costi e di prendere decisioni informate sui prezzi e sui livelli di produzione. Ad esempio, identificando il punto in cui il costo totale medio inizia ad aumentare, il produttore può determinare la quantità di produzione più efficiente per massimizzare i profitti. Inoltre, comprendendo il costo marginale, il produttore può decidere quanto sia redditizio continuare ad aumentare la produzione. | |||
== | == Esempio: costo totale == | ||
Questo grafico mostra una curva di costo totale tracciata rispetto alla quantità di pizze prodotte all'ora. La curva mostra una relazione positiva tra il costo totale e il numero di pizze prodotte, indicando che il costo totale aumenta con la produzione. | |||
[[Fichier:Exemple cout total 1.png|400px|vignette|centré]] | [[Fichier:Exemple cout total 1.png|400px|vignette|centré]] | ||
Inizialmente, la curva sembra aumentare a un tasso relativamente costante, il che potrebbe indicare che i costi variabili dominano i costi totali dopo la copertura dei costi fissi. Questo è coerente con il comportamento tipico dei costi variabili, che aumentano in proporzione alla quantità prodotta. All'aumentare della produzione, si nota che la pendenza della curva diventa più ripida. Ciò suggerisce che il costo di produzione di ogni pizza aggiuntiva aumenta, il che può essere dovuto a diversi fattori, come la diminuzione dei rendimenti marginali, in cui l'aggiunta di più manodopera o di altre risorse non comporta un aumento proporzionale della produzione. | |||
La | La pendenza crescente della curva dei costi totali può anche riflettere il fatto che l'azienda ha raggiunto la sua capacità produttiva ottimale e la produzione di ulteriori pizze richiede investimenti sproporzionati in fattori produttivi. Ad esempio, se la capacità del forno è massima, la produzione di pizze aggiuntive potrebbe richiedere l'uso di un forno supplementare o di straordinari per il personale, con un conseguente aumento del costo unitario. | ||
L' | L'analisi di questa curva è essenziale per le decisioni di gestione della produzione. Può aiutare il produttore a identificare il livello di produzione più redditizio e a valutare se i costi attuali sono sostenibili nel lungo periodo. Se l'andamento della curva continua, il produttore potrebbe dover riconsiderare il proprio processo produttivo, investire in attrezzature più efficienti o riadattare la propria strategia di prezzo per garantire che l'aumento dei costi non intacchi i profitti. | ||
== | == Esempio: costo marginale == | ||
Il costo marginale riflette l'aumento del costo totale dovuto alla produzione di un'unità aggiuntiva di un bene o servizio. In un contesto di produttività decrescente, caratteristica della legge dei rendimenti marginali decrescenti, il costo marginale tende ad aumentare all'aumentare della quantità prodotta. Questo accade perché ogni unità aggiuntiva richiede maggiori input o sforzi per essere prodotta, a causa di vincoli di capacità o della maggiore inefficienza dei fattori di produzione aggiuntivi. | |||
Poiché il costo fisso (FC) rimane costante indipendentemente dal livello di produzione, qualsiasi aumento del costo totale quando viene prodotta un'unità aggiuntiva è dovuto a un aumento del costo variabile (VC). Il costo marginale è quindi una misura diretta della variazione del costo variabile. Matematicamente, può essere espresso come segue: | |||
<math> Cm = \frac{\Delta CV}{\Delta q} </math> | <math> Cm = \frac{\Delta CV}{\Delta q} </math> | ||
Ciò implica che il costo marginale è uguale alla pendenza della curva dei costi variabili rispetto alla quantità prodotta. In pratica, ciò significa che se il costo di produzione della prossima pizza (ad esempio) è più alto di quello della pizza precedente, ciò è dovuto all'aumento dei costi variabili, come la manodopera extra richiesta o i costi dei materiali extra sostenuti per mantenere la produzione. | |||
Per le imprese, la comprensione del costo marginale è essenziale per prendere decisioni ottimali in materia di produzione e di prezzi. Produrre oltre il punto in cui il costo marginale inizia a superare il prezzo di vendita può ridurre la redditività. Per questo motivo, le aziende in genere mirano a regolare il proprio livello di produzione per mantenere il costo marginale il più basso possibile, soddisfacendo al contempo la domanda del mercato. | |||
[[Fichier:Exemple de cout marginal 1.png|400px|vignette|centré]] | [[Fichier:Exemple de cout marginal 1.png|400px|vignette|centré]] | ||
Il grafico mostra una curva lineare ascendente che rappresenta il costo marginale (MC) in funzione della quantità prodotta. L'asse verticale rappresenta i costi in CHF (franchi svizzeri), mentre l'asse orizzontale rappresenta la quantità di beni prodotti. | |||
La | La linea retta indica che il costo marginale rimane costante per ogni unità aggiuntiva prodotta. Ciò suggerisce che per ogni unità aggiuntiva prodotta, il costo aggiuntivo sostenuto dall'azienda rimane lo stesso. Questo tipo di relazione lineare è tipica di una situazione in cui i costi variabili non aumentano con la produzione, come potrebbe accadere se l'azienda opera in un'area di produzione con rendimenti costanti. | ||
Tuttavia, questa situazione è abbastanza ideale e non è spesso osservata nella realtà su lunghi periodi di produzione o su larga scala, poiché la maggior parte delle aziende si troverà ad affrontare rendimenti marginali decrescenti ad un certo punto. In parole povere, ciò significa che la curva del costo marginale è generalmente a forma di U, inizia con una pendenza negativa, raggiunge un minimo e poi diventa positiva con l'aumento della produzione. | |||
La | La situazione rappresentata da questo grafico potrebbe verificarsi in un contesto in cui l'azienda dispone di una capacità produttiva sufficiente e di risorse, come materie prime e manodopera, che possono essere facilmente e uniformemente aumentate per incrementare la produzione senza incorrere in significativi costi aggiuntivi. | ||
Per l'azienda, un costo marginale costante significa che la pianificazione della produzione può essere effettuata con un certo grado di prevedibilità in termini di costi. Ciò facilita le decisioni in materia di prezzi e di espansione, poiché la struttura dei costi non varia con l'aumento o la diminuzione della produzione. Tuttavia, l'azienda deve sempre monitorare la situazione per individuare eventuali segnali di cambiamento nell'andamento del costo marginale, poiché gli aumenti potrebbero indicare crescenti inefficienze o imminenti vincoli di capacità. | |||
== | == Esempio: costo medio == | ||
Il comportamento del costo medio è caratteristico di molte strutture produttive ed è un concetto essenziale in economia. La curva a U del costo medio riflette le diverse fasi della produzione e l'efficienza dei costi. | |||
Nella fase iniziale della produzione, i costi medi tendono a diminuire all'aumentare della quantità prodotta. Ciò è dovuto alla distribuzione dei costi fissi su un numero crescente di unità prodotte. Quando la produzione è bassa, ogni unità prodotta deve sostenere gran parte dei costi fissi, rendendo il costo medio per unità relativamente alto. Tuttavia, quando la produzione aumenta, i costi fissi vengono distribuiti su un numero maggiore di unità, riducendo il costo medio per unità. Questa riduzione continua fino a quando l'azienda non raggiunge le cosiddette economie di scala. | |||
Quando la produzione continua ad aumentare oltre questo punto, l'azienda può incontrare rendimenti di scala decrescenti. Ciò significa che i costi variabili iniziano ad avere un impatto più significativo sui costi totali. I costi variabili medi possono aumentare a causa della diminuzione della produttività marginale dei fattori produttivi aggiuntivi. Ad esempio, l'azienda può essere costretta a pagare gli straordinari ai lavoratori o ad affrontare costi di input più elevati a causa dell'aumento della domanda. Di conseguenza, il costo medio inizia ad aumentare, dando alla curva del costo medio la sua caratteristica forma a U. | |||
Questa forma a U implica che esiste un livello ottimale di produzione in cui il costo medio è ridotto al minimo. Per un'azienda, l'identificazione di questo livello è fondamentale perché massimizza l'efficienza e la redditività. Produrre meno di questo livello significa che l'azienda non sta sfruttando appieno la sua capacità produttiva e le sue economie di scala, mentre produrre di più significa che l'azienda sta affrontando inefficienze crescenti e costi marginali in aumento. Pertanto, capire dove si colloca la propria produzione rispetto a questa curva a U è essenziale per le aziende quando prendono decisioni strategiche sui livelli di produzione e di prezzo. | |||
[[Fichier:Exemple de cout moyen 1.png|400px|vignette|centré]] | [[Fichier:Exemple de cout moyen 1.png|400px|vignette|centré]] | ||
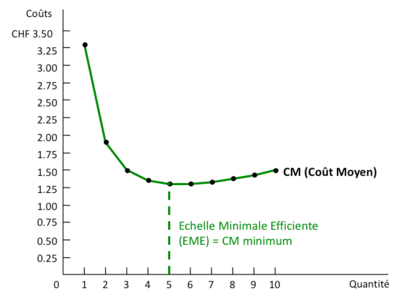
Il grafico mostra la curva del costo medio (CA) in funzione della quantità prodotta, in franchi svizzeri (CHF). Come previsto, la curva ha una forma a U, che indica che il costo medio per unità inizialmente diminuisce con l'aumento della produzione, raggiunge un punto di minimo e poi inizia a crescere con l'aumento della produzione. | |||
Inizialmente, quando la produzione è molto bassa, il costo medio è elevato a causa della distribuzione dei costi fissi su un numero ridotto di unità. Con l'aumento della produzione, i costi fissi vengono distribuiti su un numero maggiore di unità, facendo diminuire il costo medio per unità. La parte discendente della curva rappresenta le economie di scala ottenute con l'aumento della produzione. È in questa fase che l'azienda diventa più efficiente, riducendo i costi medi. | |||
Il punto più basso della curva corrisponde alla Scala Minima Efficiente (MES), ovvero il livello di produzione in cui il costo medio è minimo. A questo punto, l'azienda opera in modo ottimale, non potendo produrre un'unità aggiuntiva a un costo medio inferiore. Questo è il livello di produzione più efficiente per l'azienda. | |||
Al di là dell'MSE, il costo medio inizia ad aumentare, suggerendo che l'azienda sta affrontando rendimenti marginali decrescenti. Quando la produzione aumenta oltre questo punto, ogni unità aggiuntiva costa di più, in parte a causa dell'aumento del costo medio variabile che potrebbe essere causato dall'esaurimento della capacità produttiva, dalla necessità di investire in attrezzature aggiuntive o più costose, o dall'assunzione di manodopera aggiuntiva a tariffe più elevate. | |||
È fondamentale per un'azienda riconoscere dove si trova la sua EME e cercare di massimizzare la produzione intorno a quel punto per minimizzare i costi medi e massimizzare i profitti. Se un'azienda produce meno della sua EME, non è efficiente come potrebbe. Se produce di più, rischia di aumentare inutilmente i costi, il che potrebbe danneggiare la sua competitività sul mercato. | |||
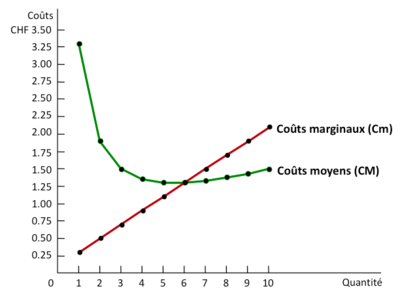
== | == Costo marginale e costo medio == | ||
La | La relazione tra costo marginale (MC) e costo medio (AC) è un aspetto fondamentale della teoria economica della produzione. Il costo marginale è il costo di produzione di un'unità aggiuntiva, mentre il costo medio è il costo totale diviso per il numero di unità prodotte. La loro interazione determina la dinamica della produzione e dei costi di un'azienda. | ||
Il costo marginale svolge un ruolo decisivo nel comportamento del costo medio: | |||
* | * Quando il costo marginale è inferiore al costo medio, ogni unità aggiuntiva prodotta costa meno del costo medio corrente, con l'effetto di far scendere il costo medio. Questo si verifica tipicamente quando l'azienda aumenta la produzione partendo da un basso livello di output, beneficiando delle economie di scala e dell'ammortamento dei costi fissi su un numero maggiore di unità; * quando il costo marginale è superiore al costo medio, significa che il costo di produzione di ogni unità aggiuntiva è superiore al costo medio attuale, con conseguente aumento del costo medio. Questo può accadere quando l'azienda ha superato il punto di massima efficienza e si trova di fronte a rendimenti marginali decrescenti, in cui l'aumento della produzione comporta un aumento proporzionale dei costi. | ||
* | |||
Il punto in cui il costo marginale interseca il costo medio è particolarmente significativo. Questo si verifica al minimo del costo medio, che è anche la scala minima di efficienza (MES). Al MERS, l'azienda produce a un livello in cui il costo medio per unità è il più basso possibile. Se la produzione aumenta oltre questo punto, il costo marginale, essendo più alto del costo medio, farà aumentare il costo medio. | |||
In pratica, un'azienda cercherà di produrre a un livello in cui il costo marginale è uguale al costo medio, cioè all'EME, perché è qui che la produzione è più efficiente in termini di costi. Produrre meno dell'EME significa che l'azienda non è efficiente come potrebbe, mentre produrre di più significa che l'azienda sta incontrando inefficienze e aumentando i costi. | |||
[[Fichier:Coût marginal et coût moyen 1.png|400px|vignette|centré]] | [[Fichier:Coût marginal et coût moyen 1.png|400px|vignette|centré]] | ||
Il grafico mostra due curve distinte: la curva del costo marginale (Cm) in rosso e la curva del costo medio (CM) in verde, tracciate rispetto alla quantità prodotta, con il costo espresso in franchi svizzeri (CHF). | |||
La | La curva del costo medio ha la caratteristica forma a U di cui abbiamo parlato: diminuisce rapidamente all'inizio, riflettendo le economie di scala e l'ammortamento dei costi fissi su un numero crescente di unità. Il punto più basso della curva del costo medio rappresenta la Scala Minima Efficiente (MES), dove il costo medio per unità è al minimo. Dopo questo punto, la curva inizia a salire, suggerendo che i costi medi aumentano all'aumentare della quantità prodotta, probabilmente a causa della diminuzione dei rendimenti marginali e dell'aumento dei costi variabili medi. | ||
La | La curva dei costi marginali inizia al di sopra della curva dei costi medi e la incrocia proprio in corrispondenza dell'EME. Prima di questo punto di incrocio, il costo marginale è inferiore al costo medio, il che significa che l'aggiunta di ulteriori unità di produzione riduce il costo medio. Dopo il punto di incrocio, il costo marginale diventa più alto del costo medio, indicando che ogni unità aggiuntiva costa più del costo medio, con conseguente aumento del costo medio. | ||
Questo grafico illustra l'importante principio economico secondo cui il costo marginale interseca il costo medio nel suo punto minimo. Ciò significa che l'azienda sta producendo all'EME, il livello di produzione più efficiente in termini di costi. Se la produzione dovesse aumentare oltre questo punto, diventerebbe meno efficiente, come dimostra l'aumento del costo medio. | |||
Per un'azienda, comprendere la relazione tra costo marginale e costo medio è fondamentale per ottimizzare la produzione e massimizzare i profitti. Gestire la produzione in modo da mantenere i costi il più possibile vicini al livello EME può aiutare a garantire che l'azienda operi in modo efficiente e redditizio. | |||
== | == Costo medio (fisso e variabile) == | ||
Il costo fisso medio (AFC) e il costo variabile medio (AVC) sono due componenti del costo totale medio (ATC). Ciascuna misura una parte diversa dei costi totali per unità prodotta. | |||
Costo fisso medio (AFC): Il costo fisso medio è calcolato dividendo il costo fisso totale (FC) per la quantità di beni prodotti (q). I costi fissi sono costi che non cambiano con la quantità prodotta, come l'affitto, gli stipendi dei dipendenti non direttamente coinvolti nella produzione, l'ammortamento dei macchinari e le assicurazioni. La formula del costo fisso medio è la seguente: <math> AFC = \frac{CF}{q} </math> | |||
<math> | |||
All'aumentare della produzione, l'AMC diminuisce perché i costi fissi sono distribuiti su un numero maggiore di unità. Ad esempio, se l'affitto di un'officina è di 1.000 euro al mese e l'officina produce 100 unità, l'AMC è di 10 euro per unità. Se la produzione raddoppia a 200 unità, il CMF scende a 5 euro per unità. | |||
Costo variabile medio (AVC): il costo variabile medio si ottiene dividendo il costo variabile totale (CV) per la quantità prodotta. I costi variabili variano direttamente con la quantità prodotta e comprendono voci come le materie prime, l'energia consumata nella produzione e i salari dei lavoratori pagati a ore. La formula per il costo variabile medio è: <math> AVC = \frac{CV}{q} </math> | |||
<math> | |||
L'AVC può rimanere costante se i costi per unità di input rimangono invariati all'aumentare della produzione, ma può anche variare in base a diversi fattori, come i risparmi sugli acquisti in blocco o l'esaurimento delle risorse che richiedono input più costosi. | |||
In breve, il costo medio totale, che è la somma dell'FPC e del GPC, fornisce una panoramica del costo unitario per l'intera produzione. La comprensione di questi costi medi consente alle aziende di determinare il prezzo di vendita dei loro prodotti, di pianificare i livelli di produzione e di effettuare analisi di redditività. | |||
[[Fichier:Coût moyens (fixe et variable).png|400px|vignette|centré]] | [[Fichier:Coût moyens (fixe et variable).png|400px|vignette|centré]] | ||
== | == Più in generale == | ||
La | La produttività marginale è inizialmente crescente (specializzazione dei lavoratori nelle loro mansioni) e poi decrescente (perché i fattori fissi devono essere condivisi da un numero crescente di lavoratori). | ||
[[Fichier:Couts moyen (fixe et variable)2.png|400px|vignette|centré]] | [[Fichier:Couts moyen (fixe et variable)2.png|400px|vignette|centré]] | ||
Il grafico mostra quattro curve che illustrano la relazione tra i costi di produzione e la quantità prodotta in unità. | |||
# | # Costi fissi medi (AFC): questa curva grigia mostra che il costo fisso medio diminuisce costantemente all'aumentare della quantità prodotta. Ciò è dovuto al fatto che i costi fissi (come l'affitto, gli stipendi dei dipendenti fissi, ecc.) vengono distribuiti su un numero maggiore di unità, diminuendo così il costo attribuito a ogni unità aggiuntiva. | ||
# | # Costi variabili medi (AVC): la curva marrone rappresenta i costi variabili medi che, in questo caso, sembrano inizialmente diminuire con l'aumentare della produzione, raggiungendo un punto di minimo e poi aumentando nuovamente. Il punto più basso rappresenta il punto in cui l'azienda beneficia pienamente delle economie di scala sui costi variabili. L'inclinazione verso l'alto della curva suggerisce che, dopo un certo punto, l'azienda inizia a sperimentare rendimenti marginali decrescenti, portando a un aumento dei costi variabili per unità. | ||
# | # Costo medio (CA): la curva verde indica il costo medio totale, che è la somma del CA e del CA. Segue la classica forma a U, scendendo inizialmente con le economie di scala e poi risalendo a causa dei rendimenti marginali decrescenti. Il punto più basso di questa curva indica l'efficienza produttiva ottimale dell'azienda, dove il costo totale medio per unità è il più basso. | ||
# | # Costi marginali (MC): La curva rossa traccia il costo marginale, ovvero il costo di produzione di un'unità aggiuntiva. Questa curva inizia al di sotto della curva del costo medio, la incrocia nel punto più basso della curva del costo medio (che è anche la Scala Minima Efficiente o MES) e poi continua a salire. Ciò conferma la regola secondo cui quando il costo marginale è inferiore al costo medio, il costo medio diminuisce, mentre quando il costo marginale è superiore al costo medio, il costo medio aumenta. | ||
Le osservazioni fatte nel grafico supportano i principi economici standard, secondo i quali il costo medio raggiunge un minimo quando il costo marginale è uguale al costo medio. Il grafico mostra anche chiaramente che il costo medio variabile è sempre inferiore al costo marginale dopo il punto in cui i costi medi iniziano a crescere, il che è coerente con l'idea che il costo di produzione di un'unità aggiuntiva sia più alto all'aumentare della produzione. Il grafico indica inoltre che il costo marginale incontra il costo medio in corrispondenza dell'EME, dove il costo medio è più basso, un punto di riferimento importante per le decisioni di produzione e di prezzo. | |||
== | == Proprietà == | ||
Le tre proprietà seguenti sono principi fondamentali nella teoria economica delle funzioni di costo e hanno implicazioni dirette per la gestione della produzione e la strategia dei prezzi aziendali. | |||
# | # Costo marginale crescente: la proprietà secondo cui il costo marginale aumenterà con la quantità prodotta è legata alla legge dei rendimenti marginali decrescenti. Ciò significa che, nella maggior parte dei processi produttivi, l'aggiunta di ulteriori unità di input (come il lavoro o il capitale) a un certo punto si tradurrà in un aumento meno che proporzionale della produzione. Ciò può essere dovuto a vincoli di capacità, a inefficienze crescenti o a costi aggiuntivi delle risorse. L'aumento del costo marginale riflette il costo aggiuntivo della produzione di un'unità supplementare, che aumenta all'aumentare della quantità di prodotto. | ||
# | # Forma a U del costo medio : La forma a U del costo medio deriva dal modo in cui i costi fissi e variabili si comportano al variare della produzione. All'inizio della produzione, i costi medi diminuiscono perché i costi fissi sono distribuiti su un numero crescente di unità. Tuttavia, una volta che la produzione raggiunge e supera l'EME, i costi variabili medi iniziano a pesare di più sul costo totale, portando a un aumento del costo medio. Se il costo marginale fosse sempre decrescente, ciò significherebbe che l'azienda continuerebbe indefinitamente a guadagnare in efficienza con ogni unità aggiuntiva prodotta, il che non è realistico nella maggior parte dei casi a causa di vincoli fisici e pratici. | ||
# | # Intersezione del costo marginale e medio : Il punto in cui il costo marginale interseca il costo medio è fondamentale perché rappresenta il livello di produzione in cui il costo medio è al minimo - la Scala Minima Efficiente (MES). A questo punto, l'aggiunta di altre unità inizia ad aumentare il costo medio, il che significa che l'azienda perde efficienza oltre questo punto. Questo incrocio è quindi un indicatore per l'azienda che ha raggiunto la sua capacità produttiva più efficiente. | ||
Queste proprietà hanno conseguenze pratiche per le aziende. Per massimizzare la redditività, un'azienda dovrebbe cercare di operare al livello EME, dove può minimizzare i costi medi e quindi massimizzare i profitti. Ciò richiede una comprensione approfondita della struttura dei costi e della capacità produttiva. Inoltre, le aziende devono prestare molta attenzione alla gestione della produzione, in modo da non superare il punto in cui i costi marginali iniziano ad aumentare, il che potrebbe portare a una produzione inefficiente e a perdite. | |||
== | == Riassunto grafico == | ||
L' | L'immagine seguente è una sintesi grafica che rappresenta le relazioni tra costo marginale (MC), costo medio variabile (AVC), costo medio totale (ATC) e costo variabile (VC(q)), in due contesti diversi: quando i costi fissi (FC) sono nulli e quando i costi fissi sono positivi. | ||
[[Fichier:Propriétés_des_couts.png|400px|vignette|centré]] | [[Fichier:Propriétés_des_couts.png|400px|vignette|centré]] | ||
L' | L'immagine visualizzata è una sintesi grafica che rappresenta le relazioni tra costo marginale (MC), costo medio variabile (AVC), costo medio totale (ATC) e costo variabile (VC(q)), in due diversi contesti: quando i costi fissi (FC) sono nulli e quando i costi fissi sono positivi. | ||
In entrambi i grafici, le curve del costo marginale (linea arancione tratteggiata), del costo variabile medio (linea marrone) e del costo totale medio (linea verde) presentano caratteristiche tipiche: | |||
# | # Quando CF=0: | ||
#* La | #* La curva del costo medio variabile (AVC) e quella del costo medio totale (ATC) partono dallo stesso punto sull'asse delle ordinate perché non ci sono costi fissi da ammortizzare sulle unità prodotte. | ||
#* | #* Le curve AVC e ATC inizialmente diminuiscono, raggiungono un punto di minimo e poi iniziano a crescere, formando la classica curva a U che rappresenta economie e poi diseconomie di scala. | ||
#* | #* Il costo marginale (MC) interseca le curve MVC e MTC nel loro punto minimo, che è il punto di inflessione in cui il costo marginale inizia a superare il costo medio variabile e il costo totale, indicando che produrre un'unità aggiuntiva diventa più costoso della media. | ||
# | # Quando CF>0: | ||
#* La | #* La curva CVM parte dall'origine perché i costi variabili sono pari a zero quando la produzione è pari a zero. | ||
#* La | #* La curva CTM parte sopra l'origine al livello di costi fissi positivi, perché anche senza produzione l'azienda deve coprire i costi fissi. | ||
#* | #* Come in precedenza, le curve CVM e CTM mostrano una diminuzione dei costi medi con l'aumento iniziale della produzione, seguita da un aumento dopo aver raggiunto un minimo. | ||
#* | #* Il costo marginale segue la stessa traiettoria del primo grafico, ma è importante notare che il punto in cui il Cm interseca il CTM è più alto sull'asse dei costi a causa della presenza dei costi fissi. | ||
In entrambi i casi, la posizione in cui il Cm interseca il CVM e il CTM è cruciale per le decisioni sulla produzione. È a questo punto che l'azienda non beneficia più delle economie di scala e deve rivalutare l'aumento della produzione per evitare costosi aumenti dei costi medi. | |||
I grafici illustrano chiaramente l'importanza dei costi fissi nel determinare il costo medio totale e mostrano che le aziende devono prendere in considerazione sia i costi fissi che quelli variabili quando analizzano le loro strutture di costo. Dovrebbero cercare di massimizzare la produzione laddove il costo medio è ridotto al minimo, pur riconoscendo che l'aumento della capacità produttiva può portare a costi più elevati nel lungo periodo se si verificano rendimenti marginali decrescenti. | |||
== | == Esempio numerico == | ||
L' | L'azienda manifatturiera ha una funzione di costo totale complessa che incorpora termini lineari, quadratici e cubici, oltre a un costo fisso. Per questa azienda, le diverse categorie di costo possono essere riassunte come segue: | ||
# | #Costo totale (TC(q)): Si tratta della funzione che rappresenta la somma totale dei costi fissi e variabili in funzione della quantità prodotta q. Per l'azienda, il costo totale è dato dalla formula: <math> CT(q) = 100q - 4q^2 + 0,2q^3 + 450 </math> #Costo fisso (CF): è un costo che non varia con la quantità prodotta ed è qui rappresentato da un valore di 450. #Costo variabile (CV(q)): È la parte del costo totale che varia con la quantità prodotta. La funzione del costo variabile è: <math> CV(q) = 100q - 4q^2 + 0,2q^3 </math> #Costo marginale (Cm(q)): È il costo aggiuntivo della produzione di un'unità supplementare. Si ricava prendendo la derivata prima della funzione di costo totale rispetto a q : <math> Cm(q) = \frac{\partial CT}{\partial q} = 100 - 8q + 0.6q^2 </math> | ||
# | #Costo fisso medio (CFM(q)): È il costo fisso ripartito su ogni unità prodotta. Diminuisce all'aumentare della quantità prodotta: <math> CFM(q) = \frac{CF}{q} = \frac{450}{q} </math> | ||
# | #Costo medio variabile (AVC(q)): È il costo variabile per unità prodotta : <math> CVM(q) = \frac{CV(q)}{q} = 100 - 4q + 0.2q^2 </math> | ||
# | #Costo medio (CM(q)): È il costo totale per unità prodotta, pari alla somma del costo fisso medio e del costo variabile medio: <math> CM(q) = \frac{CT(q)}{q} = 100 - 4q + 0.2q^2 + \frac{450}{q} </math> | ||
# | |||
# | |||
# | |||
Queste formule forniscono una panoramica completa della struttura dei costi dell'azienda e sono essenziali per valutare le prestazioni economiche e prendere decisioni strategiche sulla produzione e sui prezzi. | |||
== | == Legame tra la funzione di produzione e i costi == | ||
La | La funzione di costo totale può essere vista come un riflesso della funzione di produzione, con un'attenzione particolare agli input e ai costi piuttosto che agli output. | ||
In questa interpretazione : | |||
# | # Funzione di produzione inversa: per una data quantità di output q e con uno stock fisso di capitale fisico K, la funzione di produzione inversa indica il numero di ore di lavoro L necessarie per produrre q. Ciò si basa sull'ipotesi che la tecnologia di produzione e l'efficienza siano già stabilite. | ||
# | # Costo salariale e costo variabile (VC): moltiplicando queste ore di lavoro per il salario orario w si ottiene il costo salariale, che in questo caso sarebbe il costo variabile totale, assumendo che il lavoro sia l'unico input variabile. La massa salariale è quindi funzione della quantità prodotta q e dello stock di capitale K: Massa salariale = w ⋅ L (K, q) | ||
# | # Costo totale (TC): Infine, per ottenere il costo totale, aggiungiamo al costo variabile (massa salariale) il costo fisso, che è il costo generato dal capitale fisico (ad es. ammortamento, affitto, manutenzione): TC (K, q) = w ⋅ L (K, q) + Costo fisso. | ||
Questo modo di concepire le funzioni di costo totale come inversione delle funzioni di produzione è particolarmente utile quando si considera la teoria dell'impresa in un contesto produttivo in cui le decisioni di produzione sono prese sulla base dei costi dei fattori produttivi e dell'efficienza del loro utilizzo. Questo metodo sottolinea l'importanza della gestione delle risorse e la necessità di ottimizzare i fattori produttivi per minimizzare i costi e massimizzare i profitti. | |||
[[Fichier:Lien entre fonction de production et coûts 1.png|500px|vignette|centré]] | [[Fichier:Lien entre fonction de production et coûts 1.png|500px|vignette|centré]] | ||
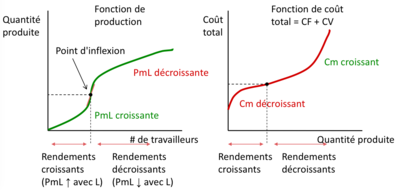
Questi due grafici illustrano la relazione tra la quantità di lavoro richiesta e i costi variabili per produrre diverse quantità di un bene in una funzione di produzione di breve periodo con uno stock di capitale fisso (K). | |||
# | # Grafico della funzione lavoro: nel primo grafico (a sinistra), l'asse verticale (L) rappresenta la quantità di lavoro richiesta e l'asse orizzontale (q) rappresenta la quantità di bene prodotto. La curva mostra le fasi di rendimento crescente e decrescente del lavoro. Inizialmente, all'aumentare della quantità prodotta, è necessaria meno manodopera per ogni unità aggiuntiva prodotta, il che è caratteristico dei rendimenti crescenti. Tuttavia, dopo aver raggiunto un certo livello di produzione (punto di inflessione), la quantità di lavoro richiesta per produrre ogni unità aggiuntiva inizia ad aumentare, indicando rendimenti decrescenti. | ||
# | # Grafico della funzione di costo variabile: nel secondo grafico (a destra), l'asse verticale rappresenta il costo variabile totale (VC) e l'asse orizzontale rappresenta anche la quantità del bene prodotto. La curva mostra il costo variabile di produzione associato a ciascun livello di produzione. Il costo variabile è calcolato moltiplicando la quantità di manodopera (L) per il salario orario (w), che dà il costo del lavoro. Questa curva riflette la forma della curva del lavoro, dove i costi variabili per unità inizialmente diminuiscono a causa dei rendimenti crescenti, ma poi aumentano a causa dei rendimenti decrescenti del lavoro. | ||
I due grafici illustrano come la funzione di produzione possa essere "invertita" per determinare i costi variabili associati alla produzione di diversi livelli di output. Il concetto di rendimenti decrescenti è fondamentale per capire perché, dopo un certo punto, produrre di più diventa sempre più costoso per l'azienda. Questa informazione è fondamentale per la pianificazione della produzione e per la definizione delle strategie di prezzo, in quanto aiuta a identificare il punto di produzione più efficiente e redditizio. | |||
In pratica, questa analisi può aiutare le aziende a decidere quanti lavoratori assumere e quanto produrre per minimizzare i costi e massimizzare i profitti. Le aziende devono fare attenzione a non produrre oltre il punto in cui i costi marginali superano i costi medi, poiché ciò potrebbe ridurre i profitti complessivi. | |||
[[Fichier:Lien entre fonction de production et coûts 2.png|500px|vignette|centré]] | [[Fichier:Lien entre fonction de production et coûts 2.png|500px|vignette|centré]] | ||
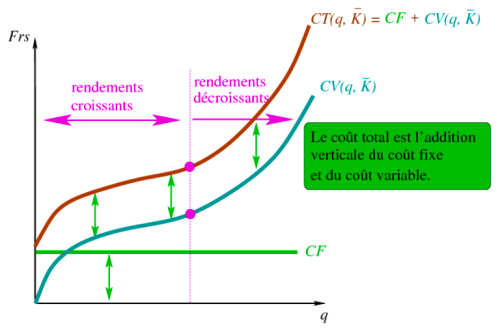
Questo grafico illustra la struttura dei costi di un'azienda, evidenziando come si compongono i costi totali e come si evolvono con la quantità prodotta. | |||
Il grafico presenta due curve principali: | |||
# La | # La curva dei costi variabili (CV(q, K)): Questa curva mostra come i costi variabili cambiano con la quantità prodotta (q). La curva inizia nell'origine, indicando che non ci sono costi variabili se la produzione è pari a zero. La curva dapprima sale meno ripidamente, poi diventa più ripida, indicando prima un aumento e poi una diminuzione dei rendimenti del lavoro. Ciò significa che per ogni unità aggiuntiva prodotta, il costo variabile aumenta inizialmente a un tasso decrescente (efficienza crescente), poi a un tasso crescente (efficienza decrescente) a causa della legge dei rendimenti marginali decrescenti. | ||
# La | # La curva del costo totale (CT(q, K)) : Il costo totale è rappresentato dalla somma verticale dei costi fissi (FC) e dei costi variabili (VC). La curva di costo totale inizia dai costi fissi, perché anche senza produzione l'azienda deve sostenere questi costi. La curva TC ha la stessa forma della curva CV, ma è spostata verso l'alto dal valore dei costi fissi. | ||
I costi fissi (FC) sono rappresentati da una linea orizzontale, il che è logico in quanto i costi fissi non cambiano indipendentemente dalla quantità prodotta. Il punto in cui la curva dei costi variabili cambia pendenza (il punto di decrescita) è anche il punto in cui la curva dei costi totali cambia pendenza. Questo punto è cruciale perché indica la quantità di produzione in cui l'efficienza inizia a diminuire. | |||
Il grafico illustra anche che il costo totale per ogni livello di produzione è sempre superiore ai costi variabili a causa dell'aggiunta dei costi fissi. Ciò sottolinea l'importanza per le aziende di coprire non solo i costi variabili, ma anche i costi fissi, al fine di raggiungere la redditività. In sintesi, il grafico è uno strumento utile per visualizzare i costi di produzione e capire come cambia l'efficienza produttiva all'aumentare della quantità prodotta. Per le aziende, la comprensione di queste relazioni è fondamentale per ottimizzare la produzione, stabilire i prezzi e massimizzare i profitti. | |||
= | = Breve e lungo termine = | ||
== | == La funzione di produzione a breve e a lungo termine == | ||
In economia è necessario distinguere tra la nozione di produzione a breve e a lungo termine. Nel quadro di breve termine, almeno uno dei fattori di produzione è fisso, spesso il capitale (K), mentre gli altri fattori, come il lavoro (L), possono variare. Ciò riflette situazioni in cui l'azienda può modificare rapidamente la quantità di manodopera impiegata, ma non può cambiare altrettanto facilmente la propria capacità di capitale a causa di impegni a lungo termine, tempi di consegna di nuovi macchinari o semplicemente perché gli adeguamenti del capitale richiedono importanti investimenti e decisioni strategiche. | |||
In un quadro di lungo periodo, il presupposto cambia: tutti i fattori di produzione, compreso il capitale, sono considerati variabili. Ciò consente all'azienda di adattare tutte le sue risorse per trovare la combinazione più redditizia che massimizzi il profitto. La differenza fondamentale tra l'analisi a breve e a lungo termine è la flessibilità con cui l'azienda può regolare tutti i suoi fattori produttivi. | |||
Analisi a lungo termine: | |||
# | # Scelta della produzione: nel lungo periodo, l'impresa ha la flessibilità di regolare la quantità di capitale fisico (K) e la quantità di lavoro (L) per produrre un determinato livello di output (q). Ciò significa che l'impresa può scegliere tra un insieme più ampio di combinazioni produttive per minimizzare i costi o massimizzare la produzione. | ||
# | # Isoquanti : L'impresa può utilizzare i grafici degli isoquanti per illustrare le diverse combinazioni di capitale e lavoro che producono lo stesso livello di output. Ogni isoquanto corrisponde a un diverso livello di produzione e la pendenza dell'isoquanto (tasso marginale di sostituzione tecnica) indica il tasso al quale il lavoro può sostituire il capitale mantenendo costante la produzione. | ||
# | # Massimizzazione del profitto : La massimizzazione del profitto implica la scelta del punto dell'isoquanto in cui il costo di produzione è più basso o, in altre parole, in cui l'isoquanto è tangente alla retta di isocosto. La linea di isocosto mostra tutte le combinazioni di capitale e lavoro che l'azienda può permettersi per un determinato costo totale. L'azienda modificherà la propria combinazione di capitale e lavoro fino a quando il tasso marginale di sostituzione tecnica tra lavoro e capitale sarà uguale al rapporto tra i prezzi di questi fattori. | ||
# | # Cambiamento di scala: nel lungo periodo, l'azienda può anche effettuare cambiamenti di scala aumentando proporzionalmente tutti i suoi input. Se la produzione aumenta in modo più che proporzionale rispetto agli input, si parla di rendimenti di scala crescenti. Se la produzione aumenta in modo meno che proporzionale, si parla di rendimenti di scala decrescenti. Se aumenta nella stessa proporzione, si parla di rendimenti di scala costanti. | ||
L' | L'analisi a lungo termine è essenziale per la pianificazione strategica e gli investimenti, in quanto consente all'azienda di posizionarsi in modo ottimale per la crescita futura e la competitività sul mercato. Considera l'intero processo produttivo, tenendo conto di come le decisioni di investimento e gli aggiustamenti di capacità influiscono su costi e profitti. | ||
La distinzione tra orizzonti temporali a breve e a lungo termine nella teoria economica è fondamentale per comprendere le decisioni di produzione delle imprese. | |||
La | Breve termine: nel contesto di breve termine, le imprese considerano fisse alcune risorse, in particolare il capitale fisico. Queste risorse comprendono edifici, macchinari e altre attrezzature che non possono essere modificate rapidamente o senza costi significativi. La funzione di produzione di breve periodo, denominata <math>q = f(\bar{K}, L)</math>, riflette questo vincolo: il capitale <math>bar{K}</math> è una quantità data, mentre il lavoro L può variare. I costi fissi in questo periodo includono le spese legate al capitale, come il pagamento di affitti o prestiti, che non cambiano indipendentemente dal livello di produzione. I costi variabili, invece, comprendono voci come la manodopera e le materie prime, che possono essere modificate in base alla quantità prodotta. | ||
Lungo termine: nel lungo termine, l'azienda può regolare tutti i suoi input, compreso il capitale. Questo le dà la flessibilità di ridimensionare o ristrutturare completamente le sue attività in risposta ai cambiamenti della domanda, alle innovazioni tecnologiche o ad altri fattori esterni. La funzione di produzione di lungo periodo, espressa come <math>q = f(K, L)</math>, mostra che l'impresa può scegliere la quantità di capitale K e di lavoro L da utilizzare per la produzione. A questo punto, la distinzione tra costi fissi e variabili diventa meno rilevante, poiché tutti i costi sono considerati variabili nel lungo periodo. | |||
La capacità di un'azienda di passare dalla produzione a breve termine alla pianificazione a lungo termine è fondamentale per la sua redditività e crescita a lungo termine. Le decisioni a lungo termine possono comprendere l'investimento in nuove attrezzature, l'espansione o il ridimensionamento degli impianti, o la modifica del modello aziendale per esplorare nuovi mercati o prodotti. Comprendendo e pianificando entrambi gli orizzonti, le aziende possono navigare meglio nelle condizioni di mercato e mantenere la loro competitività nel lungo periodo. | |||
== Costi di produzione nel breve e nel lungo termine == | |||
La distinzione tra costi fissi e variabili è essenziale per comprendere il processo decisionale di un'azienda in termini di produzione e di investimenti su diversi orizzonti temporali. | |||
Breve termine: nel breve termine, alcune spese non possono essere modificate rapidamente o senza costi significativi. Queste spese, come i canoni di leasing o i prestiti per le attrezzature, sono considerate costi fissi perché non cambiano con il livello di produzione. Il capitale fisico, in questo contesto, è spesso un costo fisso perché l'azienda non può facilmente acquisire o cedere i principali beni strumentali per adeguare la produzione nel breve periodo. I costi variabili, invece, possono essere modificati più facilmente e comprendono voci come le materie prime e le ore di manodopera diretta, che variano direttamente con la quantità prodotta. | |||
A lungo termine: nel lungo periodo, l'azienda ha la flessibilità di modificare tutte le sue capacità produttive, compreso il capitale fisico. Ciò significa che i costi che erano fissi nel breve periodo diventano variabili nel lungo periodo. Se si dispone di tempo sufficiente, le aziende possono effettuare investimenti strategici o disinvestimenti per aumentare o diminuire la propria capacità produttiva. Ciò include l'acquisto di nuove attrezzature, l'espansione degli impianti o addirittura la chiusura di parti dell'azienda. Queste decisioni sono guidate da considerazioni sui costi a lungo termine, con l'obiettivo di allineare la capacità produttiva alla domanda prevista e alla strategia complessiva dell'azienda. | |||
La capacità di rendere variabili i costi fissi è fondamentale per la pianificazione strategica e la competitività a lungo termine. Consente alle aziende di adattarsi ai cambiamenti dell'ambiente in cui operano, come le fluttuazioni della domanda, i progressi tecnologici e le modifiche normative. Comprendendo questi concetti, le aziende possono prevedere meglio i loro costi e benefici potenziali e adattare di conseguenza le loro strategie per mantenere una crescita e una redditività sostenibili. | |||
La natura delle funzioni di costo delle aziende varia notevolmente tra il breve e il lungo periodo, a causa della flessibilità di adattamento dei fattori di produzione. | |||
La | Nel breve periodo, l'azienda opera con fattori fissi, il che significa che deve ottimizzare la produzione regolando solo i fattori variabili. La funzione di costo di breve periodo è vincolata da questi fattori fissi (come attrezzature e impianti) che non possono essere modificati rapidamente o facilmente. Di conseguenza, l'azienda potrebbe non essere in grado di raggiungere il livello di produzione economicamente più efficiente se la domanda cambia rapidamente. | ||
Nel lungo periodo, invece, tutti i fattori diventano variabili. L'azienda può investire in nuove tecnologie, aumentare o ridurre le dimensioni dei suoi impianti e adattare la forza lavoro in modo da soddisfare esattamente le sue esigenze di produzione. Questa flessibilità permette all'azienda di raggiungere livelli di efficienza che il quadro di breve termine non consente. La funzione di costo a lungo termine offre quindi una visione più fluida e dinamica, che riflette la capacità dell'azienda di adattarsi ai cambiamenti del mercato e di ottimizzare i costi di produzione. | |||
Ciò implica che, in teoria, i costi di produzione dovrebbero essere più bassi nel lungo periodo perché l'azienda può realizzare economie di scala e beneficiare di migliori tecnologie o metodi di produzione. Tuttavia, ciò dipende anche dalla capacità dell'azienda di gestire efficacemente questi cambiamenti e di investire saggiamente in modo da ridurre i costi a lungo termine. Inoltre, gli investimenti a lungo termine sono spesso accompagnati da rischi e incertezze che possono influenzare i costi. | |||
L'analisi dei costi a lungo termine è quindi un elemento chiave della strategia aziendale, che richiede un'attenta pianificazione e valutazione delle opportunità di investimento, nonché delle condizioni di mercato che possono influenzare la domanda dei prodotti dell'azienda. | |||
== Costi medi nel breve e nel lungo periodo == | |||
I costi medi, sia a breve che a lungo termine, svolgono un ruolo fondamentale nella pianificazione finanziaria e nella strategia di un'azienda. Tuttavia, essi variano a seconda del periodo considerato, a causa della natura dei costi fissi e variabili. | |||
Costi medi a breve termine: nel breve termine, alcuni costi sono considerati fissi. Ciò significa che, indipendentemente dal livello di produzione, questi costi non cambiano. Ne sono un esempio l'affitto, gli stipendi dei dipendenti fissi e i pagamenti delle attrezzature. I costi medi di breve periodo (SRA) sono quindi influenzati dalla quantità di produzione: | |||
* Se la produzione è bassa, i costi fissi medi (CFA) sono alti perché sono distribuiti su un numero ridotto di unità; con l'aumento della produzione, i CFA per unità diminuiscono perché sono distribuiti su un numero maggiore di unità; i costi variabili medi (CVA) cambiano con la produzione, ma in misura minore rispetto ai costi fissi; i costi totali medi di breve periodo (SRAC) inizialmente diminuiscono con l'aumento della produzione (sfruttando le economie di scala), ma possono aumentare dopo aver raggiunto il punto di diminuzione dei rendimenti marginali. | |||
Costo medio di lungo periodo: nel lungo periodo, tutti i costi sono considerati variabili. Un'azienda può adattare la propria capacità produttiva modificando la quantità di capitale fisico e di lavoro utilizzati. I costi medi di lungo periodo (LRAAC) offrono una prospettiva più flessibile: | |||
* Le economie di scala possono essere ottenute aumentando la produzione, il che riduce il costo medio di lungo periodo fino a un certo punto. | |||
* I rendimenti di scala costanti si verificano quando l'aumento dei fattori produttivi porta a un aumento proporzionale della produzione, mantenendo così costante il costo medio. | |||
* I rendimenti di scala decrescenti si verificano quando l'aumento dei fattori produttivi porta a un aumento meno che proporzionale della produzione, aumentando così il costo medio. | |||
La curva del costo medio di lungo periodo (LRAEC) è spesso rappresentata come l'inviluppo delle varie curve del costo medio di breve periodo (SRAEC) per vari livelli di capacità produttiva. Essa mostra il costo medio minimo possibile per ogni livello di produzione se l'azienda ottimizza completamente tutti i suoi input. | |||
In pratica, le aziende cercano di produrre dove il costo medio di lungo periodo è più basso, in quanto indica il punto di produzione più efficiente e redditizio. È qui che un'azienda può massimizzare i profitti, in quanto produce al costo medio più basso possibile, pur avendo la flessibilità di adattarsi alle variazioni della domanda nel lungo periodo. | |||
[[Fichier:Coûts moyens dans le court et long terme 1.png|400px|vignette|centré]] | [[Fichier:Coûts moyens dans le court et long terme 1.png|400px|vignette|centré]] | ||
Il grafico mostra un'analisi comparativa dei costi medi a breve e lungo termine di un'azienda in funzione della quantità di produzione. Nel breve periodo, si osservano tre curve distinte che rappresentano i costi medi per impianti di dimensioni diverse: piccoli, medi e grandi. Ogni curva mostra un costo medio che diminuisce con l'aumentare della produzione fino a un certo punto, riflettendo le economie di scala ottenute quando i costi fissi sono distribuiti su un numero crescente di unità prodotte. Tuttavia, dopo aver raggiunto il punto più basso, i costi medi iniziano a salire di nuovo, illustrando i rendimenti marginali decrescenti in cui si sostengono costi aggiuntivi per ogni unità prodotta in più, spesso a causa del sovrautilizzo della capacità esistente o di una maggiore inefficienza. | |||
La | La curva dei costi medi di breve periodo per l'impianto piccolo raggiunge il suo minimo a un livello di produzione relativamente basso, indicando che piccole quantità di produzione sono ottimali per questa configurazione. L'impianto medio, con una capacità maggiore, raggiunge il punto di costo medio più basso a un livello di produzione più elevato, suggerendo che può produrre in modo più efficiente una quantità maggiore prima di incontrare rendimenti marginali decrescenti. Il grande impianto, con la maggiore capacità, ha il costo medio più basso a un livello di produzione ancora più alto, indicando che è meglio equipaggiato per sfruttare le economie di scala su larga scala. | ||
Al contrario, la curva in rosso, che rappresenta i costi medi a lungo termine, è una curva di inviluppo che si trova al di sotto di tutte le curve dei costi medi a breve termine. Questa curva di inviluppo riflette la flessibilità dell'azienda nell'adattare le dimensioni dell'impianto e nell'ottimizzare altri fattori di produzione su un periodo più lungo. Mostra il costo medio più basso raggiungibile a ciascun livello di produzione se l'azienda adegua perfettamente la propria capacità produttiva alle quantità desiderate. Anche questa curva raggiunge un minimo, indicando il punto di produzione più efficiente nel lungo periodo, ma a differenza delle curve a breve termine, offre una prospettiva più ampia delle opzioni di ottimizzazione disponibili per l'azienda, compresa la possibilità di scegliere tra diverse dimensioni di impianto. | |||
L' | L'analisi rappresentata in questo grafico evidenzia che le aziende tendono ad avere una maggiore flessibilità e costi potenzialmente più bassi nel lungo periodo, in quanto possono regolare tutti i fattori di produzione, compreso il capitale. Le decisioni prese oggi con impegni a lungo termine possono definire la traiettoria futura dei costi di produzione e, di conseguenza, influenzare la competitività e la redditività di un'azienda. Le aziende devono quindi valutare attentamente le loro decisioni in materia di investimenti e capacità produttiva, tenendo conto delle previsioni della domanda e degli sviluppi tecnologici, per garantire che possano produrre al livello più efficiente e redditizio possibile. | ||
== | == Economie di scala == | ||
Le economie di scala si riferiscono alla riduzione dei costi medi di lungo periodo quando un'azienda aumenta la propria produzione. La pendenza della funzione del costo medio di lungo periodo (LRAC) è un indicatore chiave della presenza di economie di scala. | |||
Se la pendenza della funzione LRAC è negativa, significa che i costi medi diminuiscono all'aumentare della quantità prodotta. Questo è il classico segnale di economie di scala: produrre di più diventa meno costoso per unità grazie a una maggiore efficienza, all'ammortamento dei costi fissi su una maggiore produzione o all'acquisizione di fattori produttivi a costi inferiori attraverso acquisti in quantità. | |||
Quando la pendenza della funzione CMLT diventa positiva, indica diseconomie di scala. Ciò può verificarsi quando l'aumento della produzione porta a un aumento dei costi medi, forse a causa di una maggiore complessità gestionale, dell'esaurimento dei benefici dell'efficienza o di vincoli operativi. | |||
Infine, se la pendenza della funzione CMLT è pari a zero, significa che l'azienda sta sperimentando rendimenti di scala costanti. In questo caso, i costi medi non cambiano all'aumentare della produzione. Ogni unità aggiuntiva ha lo stesso costo di produzione, il che indica una proporzionalità diretta tra costi e produzione. | |||
Per i responsabili delle decisioni è fondamentale capire in che posizione si trova l'azienda rispetto a queste diverse fasi delle economie di scala. Ciò consente loro di pianificare espansioni o adeguamenti della capacità produttiva con la consapevolezza di come tali cambiamenti influiranno sui costi e sulla competitività sul mercato. Le economie di scala sono spesso una forza trainante delle strategie di crescita delle aziende, in quanto possono portare a un significativo vantaggio competitivo. | |||
[[Fichier:Fonction cm Economies d’échelle.png|400px|vignette|centré]] | [[Fichier:Fonction cm Economies d’échelle.png|400px|vignette|centré]] | ||
Questo grafico illustra i concetti di economie di scala, rendimenti costanti di scala e diseconomie di scala attraverso la relazione tra costi medi e quantità di produzione. | |||
Nel grafico si possono individuare tre fasi: | |||
# | # Economie di scala: sul lato sinistro del grafico, la curva del costo medio (AC) è decrescente, a indicare che l'aumento della produzione porta a una diminuzione dei costi medi per unità. Ciò è generalmente dovuto alla distribuzione più efficiente dei costi fissi su un numero crescente di unità prodotte e a una maggiore efficienza nell'uso delle risorse. Le aziende spesso beneficiano delle economie di scala quando sono in fase di crescita o quando possono acquistare i fattori di produzione a prezzi ridotti attraverso ordini in blocco. | ||
# | # Rendimenti di scala costanti: Al centro del grafico, la curva CM si stabilizza e il costo medio per unità rimane costante nonostante l'aumento della produzione. Ciò suggerisce che l'azienda ha raggiunto un livello di produzione in cui i benefici delle economie di scala sono stati pienamente realizzati e qualsiasi ulteriore aumento della produzione non modifica il costo medio. Questo può verificarsi in situazioni in cui l'azienda opera alla sua capacità ottimale. | ||
# | # Diseconomie di scala: sul lato destro del grafico, la curva CM inizia a salire, indicando che i costi medi per unità aumentano con l'aumento della produzione. Questo può essere il risultato di un sovraccarico della capacità produttiva, di costi di gestione aggiuntivi o di una maggiore complessità operativa che rende la produzione meno efficiente all'aumentare della scala. | ||
I punti neri sulle curve indicano probabilmente i punti minimi dei costi medi per impianti di dimensioni diverse, suggerendo che ogni tipo di impianto ha una quantità ottimale di produzione. Lo spostamento da una curva all'altra riflette le variazioni della capacità produttiva che potrebbero essere ottenute con investimenti a lungo termine, consentendo all'azienda di passare a un livello più elevato di produzione efficiente con un costo medio inferiore. | |||
Questo grafico è uno strumento prezioso per prendere decisioni sugli investimenti e sulla capacità produttiva. Evidenzia l'importanza per le aziende di capire non solo dove si trovano attualmente sulla curva dei costi medi, ma anche di prevedere come le variazioni della capacità produttiva possano influire sui loro costi in futuro. Le aziende dovrebbero puntare a operare dove possono ridurre al minimo i costi medi per massimizzare i profitti, pur rimanendo attente ai rischi delle diseconomie di scala. | |||
== | == Rendimenti marginali vs. rendimenti di scala == | ||
=== | === Rendimenti marginali e rendimenti di scala === | ||
È fondamentale non confondere il rendimento marginale con i rendimenti di scala, poiché si applicano a contesti diversi e hanno implicazioni distinte per le decisioni sulla produzione. | |||
Il rendimento marginale, spesso associato alla legge dei rendimenti marginali decrescenti, si riferisce all'impatto dell'aggiunta di un'unità in più di un singolo fattore di produzione, mantenendo costanti tutti gli altri fattori. Si tratta di un'osservazione a breve termine perché esamina l'effetto immediato e diretto dell'aumento di un singolo fattore di produzione sulla produzione totale. In pratica, ciò può essere illustrato aggiungendo un lavoratore in più a una fabbrica in cui le attrezzature e lo spazio sono vincoli fissi. Inizialmente, l'aggiunta di lavoratori può aumentare significativamente la produzione, ma man mano che se ne aggiungono altri, ognuno di essi contribuirà sempre meno alla produzione totale a causa dei vincoli di spazio e di attrezzature. | |||
I rendimenti di scala, invece, esaminano come la variazione proporzionale di tutti i fattori produttivi influisca sulla produzione. Questo riflette una prospettiva a lungo termine in cui l'azienda ha la possibilità di modificare la propria struttura produttiva, comprese le dimensioni degli impianti, la quantità di macchinari e il numero di dipendenti. Le economie di scala si verificano quando il raddoppio di tutti gli input aumenta la produzione di oltre il doppio. I rendimenti di scala costanti significano che la produzione aumenta nella stessa proporzione dei fattori produttivi, mentre i rendimenti di scala decrescenti si verificano quando la produzione aumenta in misura inferiore alla proporzione in cui aumentano i fattori produttivi. | |||
La comprensione di queste differenze è fondamentale per le aziende quando prendono decisioni strategiche. Nel breve termine, l'ottimizzazione dei costi può comportare la regolazione fine degli input variabili per ottenere il miglior rendimento marginale. A lungo termine, l'azienda deve prendere in considerazione gli investimenti che possono modificare la struttura complessiva dei costi e la capacità produttiva, influenzando così i rendimenti di scala. Queste decisioni strategiche a lungo termine sono essenziali per una crescita sostenibile e per la competitività del mercato. | |||
=== | === rendimenti di scala crescenti ===== | ||
Le economie di scala, spesso associate ai rendimenti crescenti di scala, sono un fenomeno che si osserva quando le aziende aumentano la loro produzione e di conseguenza vedono diminuire i loro costi medi. Questo concetto è radicato in diversi aspetti operativi e organizzativi di un'azienda che si espande. In una grande fabbrica, ad esempio, è possibile combinare diversi compiti che, in strutture più piccole, sarebbero dispersi e gestiti in modo meno efficiente. Questo consolidamento dei compiti può portare a significativi guadagni di efficienza. | |||
Inoltre, un impianto di grandi dimensioni offre l'opportunità di una maggiore specializzazione della manodopera e del capitale. I lavoratori possono concentrarsi su compiti specifici, affinando le loro abilità e competenze attraverso la ripetizione e la concentrazione su un particolare aspetto del processo produttivo. Questa specializzazione può portare a un aumento della produttività per lavoratore. Allo stesso tempo, anche il capitale può diventare più specializzato. Le attrezzature e i macchinari progettati per funzioni specifiche possono essere utilizzati al meglio, aumentando la produttività del capitale. | |||
Un | Un altro vantaggio della produzione su larga scala è la possibilità per un'azienda di investire in manodopera altamente qualificata e in tecnologie avanzate. Mentre questi investimenti possono essere costosi e non giustificati per un'attività di piccole dimensioni, un'azienda che opera su larga scala può distribuire questi costi su una produzione più ampia, riducendo così i costi medi. Inoltre, le aziende più grandi possono spesso ottenere prezzi migliori per i loro acquisti grazie agli ordini in blocco e hanno una maggiore capacità di investire in ricerca e sviluppo, che può portare a innovazioni che riducono ulteriormente i costi nel lungo periodo. | ||
Tuttavia, è fondamentale tenere presente che questi vantaggi non sono illimitati. Quando le aziende diventano troppo grandi, possono andare incontro a diseconomie di scala, come difficoltà di gestione, problemi di comunicazione e un coordinamento meno efficace, che in ultima analisi possono portare a costi medi più elevati. Pertanto, sebbene le economie di scala possano offrire notevoli vantaggi, le aziende devono valutare attentamente fino a che punto possono crescere prima che i costi operativi e di gestione aggiuntivi inizino a superare i benefici di una produzione su larga scala. | |||
=== | === rendimenti decrescenti di scala ==== | ||
Le diseconomie di scala si verificano quando, a differenza delle economie di scala, i costi medi di un'azienda aumentano all'aumentare della quantità di produzione. Questo fenomeno è generalmente associato alla diminuzione dei rendimenti di scala e può essere attribuito a diversi fattori legati alla crescita dell'azienda. | |||
Quando un impianto raggiunge e supera una certa dimensione, l'integrazione e il coordinamento delle attività possono diventare sempre più complessi. Gestire efficacemente una grande forza lavoro e armonizzare numerose linee di produzione può rivelarsi problematico. Queste difficoltà operative possono portare a un aumento delle inefficienze, poiché la comunicazione diventa più complicata e i processi più soggetti a errori. Di conseguenza, i vantaggi derivanti dall'aumento delle dimensioni possono essere superati, se non addirittura annullati, da queste nuove sfide. | |||
Anche la motivazione e l'impegno dei dipendenti possono essere influenzati da una grande azienda. In strutture più piccole, i dipendenti possono sentirsi più coinvolti e avere una chiara comprensione dell'impatto del loro lavoro sui risultati dell'azienda. Tuttavia, in un ambiente di grandi dimensioni, il senso del contributo personale può diminuire, con conseguente riduzione della produttività e dell'efficacia complessiva. | |||
Inoltre, i sistemi di gestione possono non evolvere allo stesso ritmo delle dimensioni dell'azienda. Le strutture di gestione che funzionavano bene in una piccola o media impresa possono diventare "fattori fissi" in una grande azienda, limitando la sua capacità di adattarsi e rispondere efficacemente alle crescenti esigenze operative. Come il capitale fisico, anche il management può dover essere ridimensionato o ristrutturato per gestire efficacemente un'organizzazione più grande. | |||
Le diseconomie di scala dimostrano che esiste una dimensione ottimale per le aziende, oltre la quale l'aumento della produzione può effettivamente ridurre l'efficienza e aumentare i costi. Per questo motivo le aziende devono valutare costantemente le loro prestazioni operative e rimanere agili, anche quando crescono, per evitare le insidie delle diseconomie di scala. | |||
= | = Sintesi = | ||
L' | L'obiettivo fondamentale di un'azienda è quello di massimizzare il proprio profitto, ovvero la differenza tra i ricavi totali e i costi totali. Per raggiungere questo obiettivo, un'azienda deve non solo coprire i costi espliciti, come le spese per le materie prime, i salari e gli affitti, ma anche tenere conto dei costi impliciti. Questi ultimi rappresentano i costi opportunità associati alla produzione, come i potenziali ritorni da investimenti alternativi o il salario che l'imprenditore potrebbe guadagnare altrove. | ||
Il costo totale di un'impresa è direttamente correlato alla sua funzione di produzione, che descrive la relazione tra le quantità di input utilizzati e la quantità di output prodotto. In genere, la funzione di produzione mostra una fase di produttività marginale decrescente, il che significa che oltre un certo punto, ogni aggiunta di un fattore di produzione produce meno output aggiuntivo di quello precedente. Ciò è spesso dovuto a vincoli di capacità o a un uso meno efficiente delle risorse all'aumentare della scala di produzione. | |||
I costi aziendali si dividono in costi fissi, che rimangono costanti indipendentemente dalla quantità prodotta, e costi variabili, che variano con la produzione. I costi fissi possono includere spese come l'affitto e i salari dei dipendenti fissi, mentre i costi variabili possono includere i costi relativi alle materie prime e alla manodopera direttamente assegnata alla produzione. | |||
Il costo medio, che è il costo totale diviso per il numero di unità prodotte, fornisce una misura del costo per unità. Il costo marginale, invece, indica quanto costa produrre un'unità aggiuntiva. In molti casi, il costo marginale aumenta con la quantità prodotta, soprattutto dopo aver raggiunto un certo livello di produzione. Questo aumento è generalmente attribuito alla diminuzione della produttività marginale. | |||
Il comportamento del costo medio e del costo marginale è tale che il costo medio segue una curva a forma di U. Inizialmente diminuisce all'aumentare della produzione, a causa dell'aumento della produttività marginale. Inizialmente diminuisce all'aumentare della produzione, a causa delle economie di scala e della ripartizione dei costi fissi su un numero maggiore di unità, ma poi inizia a salire quando si affermano le diseconomie di scala. La curva del costo marginale interseca la curva del costo medio nel punto in cui il costo medio è più basso, noto come punto di minima scala efficiente. | |||
Per quanto riguarda l'orizzonte temporale, la struttura dei costi di un'azienda varia tra il breve e il lungo periodo. Molti costi considerati fissi nel breve periodo, come gli impianti e le attrezzature, possono diventare variabili nel lungo periodo, in quanto l'azienda ha la possibilità di regolare questi fattori in base alle sue decisioni di produzione. Ciò conferisce all'azienda una maggiore flessibilità per ottimizzare la struttura dei costi e quindi il potenziale di profitto a lungo termine. La capacità di un'azienda di adattare e rivedere i propri fattori produttivi nel lungo periodo è fondamentale per la sua capacità di mantenere una crescita sostenibile e di rispondere efficacemente ai cambiamenti del mercato. | |||
= Annexes = | = Annexes = | ||
Version actuelle datée du 12 janvier 2024 à 16:42
Basato su un corso di Federica Sbergami[1][2][3]
Principi e concetti di microeconomia ● Approcci metodologici al corso introduttivo di microeconomia ● Forze di mercato: domanda e offerta ● Elasticità e loro applicazioni ● Domanda, offerta e politiche governative ● Surplus del consumatore e del produttore ● Esternalità e ruolo del governo ● Principi e dilemmi dei beni pubblici nell'economia di mercato ● Costi di produzione ● Imprese in concorrenza perfetta ● Imprese in concorrenza monopolistica ● Concorrenza monopolistica ● Oligopolio ● Vincoli e preferenze dei consumatori ● Scelta del consumatore ● Problemi di informazione e scelta pubblica
L'analisi dei costi di produzione è un aspetto fondamentale dell'organizzazione industriale in microeconomia. Questa analisi è cruciale perché l'obiettivo principale di qualsiasi agente economico, in particolare delle imprese, è la massimizzazione dei profitti. Lo studio dei costi di produzione aiuta a comprendere il comportamento delle imprese in diversi contesti di mercato, tra cui la concorrenza perfetta e varie forme di concorrenza imperfetta.
I costi di produzione sono fattori chiave che influenzano le decisioni di produzione e i prezzi. In altre parole, le strategie e i programmi di un'azienda dipendono fortemente dalle sue scelte in materia di fattori produttivi. L'obiettivo finale delle aziende è quello di massimizzare i profitti e i costi di produzione, che influenzano direttamente la funzione di offerta, svolgono un ruolo significativo nel determinare i profitti.
Questa analisi consente alle aziende di prendere decisioni informate su quanto produrre, quali tecnologie utilizzare e quali prezzi praticare per rimanere competitive e massimizzare i profitti. I costi possono includere voci quali materie prime, manodopera, energia e ammortamento delle attrezzature. Comprendendo questi costi e gestendoli in modo efficace, le aziende possono ottimizzare la loro produzione e rafforzare la loro posizione sul mercato.
Analisi dei costi di produzione[modifier | modifier le wikicode]
La formula per il profitto aziendale è abbastanza semplice in teoria. L'utile (π) si calcola sottraendo i costi totali (TC) dai ricavi totali (TR). In termini matematici, si scrive :
π = RT - CT
Qui, π rappresenta il profitto, RT il ricavo totale e TC il costo totale.
Il ricavo totale (RT) si calcola moltiplicando il prezzo unitario di un bene o servizio per la quantità venduta. In altre parole :
RT= Prezzo × Quantità venduta
Questa formula evidenzia l'importanza del prezzo e del volume delle vendite nel generare ricavi per un'azienda. Un prezzo elevato o una grande quantità venduta possono entrambi aumentare i ricavi totali, mentre una gestione efficace dei costi può ridurre i costi totali, aumentando così il profitto. Tuttavia, è importante notare che questa formula semplificata non tiene conto di altri fattori che possono influenzare il profitto, come i costi fissi e variabili, le economie di scala, le condizioni di mercato e la strategia dei prezzi. In pratica, la massimizzazione del profitto è spesso più complessa e richiede un'analisi dettagliata di tutti questi fattori.
L'analisi dei costi di produzione è fondamentale per comprendere la funzione di offerta del mercato in microeconomia. Questa funzione di offerta è tradizionalmente vista come una relazione crescente tra prezzo e quantità offerta. Questa relazione si spiega con il fatto che, quando i prezzi aumentano, le aziende sono incentivate a produrre di più per ottenere maggiori profitti. I costi di produzione svolgono un ruolo fondamentale in questa dinamica. Essi comprendono sia i costi variabili, che cambiano con il livello di produzione, sia i costi fissi, che rimangono costanti indipendentemente dalla quantità prodotta. La comprensione di questi costi consente alle aziende di determinare la quantità di produzione che massimizza i loro profitti a diversi livelli di prezzo.
Parallelamente, la teoria del consumatore esamina i fattori che influenzano la funzione di domanda, che indica la quantità di un bene o servizio che i consumatori sono disposti ad acquistare a prezzi diversi. La domanda è influenzata da fattori quali il reddito dei consumatori, le loro preferenze, i prezzi dei beni sostitutivi e complementari e le loro aspettative future. L'analisi di questi fattori è essenziale per comprendere come le scelte dei consumatori influenzino la domanda complessiva del mercato.
Pertanto, l'analisi dei costi di produzione e la teoria del consumo sono due pilastri della microeconomia che si completano a vicenda per spiegare le dinamiche del mercato. Da un lato, le aziende valutano i propri costi di produzione per definire l'offerta, dall'altro i consumatori prendono le loro decisioni di acquisto in base a diversi fattori che influenzano la loro domanda. L'incontro tra domanda e offerta determina l'equilibrio del mercato, influenzando la formazione dei prezzi e la quantità di beni scambiati. Questa comprensione integrata della domanda e dell'offerta è fondamentale per analizzare l'economia del mercato, le tendenze dei consumatori e le strategie aziendali.
Questo grafico fornisce una rappresentazione visiva della struttura di base della produzione e dell'economia di un'azienda. In questo modello, gli input o i fattori di produzione, come il lavoro e il capitale, vengono acquistati sui mercati rilevanti e costituiscono la base di qualsiasi processo produttivo. Questi input vengono poi trasformati in prodotti o servizi finiti (output) utilizzando la tecnologia, che può includere metodi di produzione, attrezzature e conoscenze specialistiche.
Una volta utilizzata la tecnologia per trasformare gli input in output, questi ultimi vengono venduti sul mercato, generando ricavi per l'azienda. Tali ricavi sono funzione del prezzo di vendita dei beni o dei servizi e della quantità acquistata dai consumatori. Il diagramma suggerisce che i ricavi e i costi sono intrinsecamente legati: i costi sono una conseguenza necessaria della produzione. Questi costi includono tutto ciò che è necessario per produrre l'output, compresi, ma non solo, i salari, i costi dei materiali e l'ammortamento del capitale.
I profitti sono rappresentati per illustrare la loro natura derivata, essendo il risultato residuo una volta che i costi sono stati sottratti dai ricavi. Questo è il dato a cui le aziende sono più interessate, poiché misura l'efficienza con cui hanno trasformato i loro input in output redditizi. I profitti sono essenziali non solo per la sopravvivenza e la crescita dell'azienda, ma anche per le decisioni strategiche di investimento in nuove tecnologie o di espansione in nuovi mercati.
Questo modello schematico evidenzia anche l'importanza dei mercati dei fattori di produzione, che sono elementi chiave dell'ambiente esterno di un'azienda. Questi mercati determinano la disponibilità e il costo dei fattori di produzione essenziali, influenzando così i costi di produzione. Le aziende devono quindi monitorare attentamente questi mercati per ottimizzare le loro decisioni sui costi.
Tuttavia, è importante notare che questo diagramma è una semplificazione del processo economico reale. In realtà, le aziende si trovano ad affrontare decisioni molto più complesse, che coinvolgono una serie di fattori esterni come i cambiamenti normativi, le fluttuazioni della domanda di mercato e la rapida evoluzione della tecnologia. Inoltre, le aziende devono gestire costi fissi e variabili, economie di scala e strategie di prezzo differenziate per rimanere competitive. In sintesi, sebbene il diagramma catturi l'essenza del processo aziendale, non coglie tutte le sfumature e le complessità del mondo aziendale reale.
Funzione di produzione e costi totali[modifier | modifier le wikicode]
Che cos'è il costo di produzione?[modifier | modifier le wikicode]
Costo di opportunità[modifier | modifier le wikicode]
Il secondo principio economico riguarda un concetto fondamentale della microeconomia: il costo opportunità. Questo principio evidenzia il fatto che il costo reale di un'azione, di un investimento o di un'acquisizione non è misurato solo dalla quantità di denaro spesa per ottenerla. Al di là delle transazioni finanziarie, il costo opportunità comprende anche il valore della migliore alternativa a cui si è rinunciato per effettuare la scelta. A titolo esemplificativo, consideriamo un individuo che decide di dedicare un'ora allo studio invece che al lavoro, dove potrebbe guadagnare 20 euro. Il costo opportunità di quest'ora di studio non è solo lo sforzo o l'energia spesi per imparare, ma anche i 20 euro che non ha guadagnato lavorando. In questo modo, il costo opportunità fornisce una visione più completa e accurata delle scelte economiche.
In economia, questo concetto è fondamentale perché evidenzia il fatto che ogni scelta comporta un potenziale costo nascosto associato alla mancata selezione di un'alternativa. Le aziende e gli individui utilizzano il concetto di costo opportunità per prendere decisioni informate e razionali, confrontando i benefici attesi di un'opzione con quelli della migliore alternativa non scelta. La considerazione del costo opportunità è quindi essenziale per comprendere gli incentivi e il comportamento in economia. Costringe i decisori a considerare non solo i benefici immediati, ma anche quelli potenziali che devono essere abbandonati. Ciò garantisce che le risorse scarse siano allocate nel modo più efficiente possibile per massimizzare il valore e il benessere.
Costi espliciti vs. costi impliciti[modifier | modifier le wikicode]
Nel contesto della produzione di un bene da parte di un'azienda, i costi sono spesso classificati in due categorie: espliciti e impliciti, che riflettono i diversi aspetti dei sacrifici economici coinvolti nel processo produttivo.
I costi espliciti sono i pagamenti monetari diretti che l'impresa deve effettuare per acquisire i fattori di produzione necessari. Questi pagamenti possono includere gli stipendi pagati ai dipendenti, i prezzi di acquisto delle materie prime, gli affitti di impianti o attrezzature, gli interessi sui prestiti e qualsiasi altra spesa in contanti che possa essere registrata e contabilizzata. Spesso sono facilmente quantificabili e vengono registrati nei libri contabili dell'azienda, svolgendo un ruolo fondamentale nel calcolo dell'utile netto del bilancio.
I costi impliciti, invece, rappresentano il valore delle risorse che l'azienda ha scelto di non utilizzare per un'altra opportunità potenzialmente redditizia. Questi costi sono spesso non monetari e possono non essere evidenti nel bilancio tradizionale di un'azienda. Ad esempio, se un imprenditore utilizza un edificio di sua proprietà per la propria attività anziché affittarlo a terzi, il costo implicito è rappresentato dal potenziale affitto perso o dal reddito che avrebbe potuto generare. Allo stesso modo, se il titolare dedica il proprio tempo all'attività, il costo implicito può essere lo stipendio che avrebbe potuto guadagnare lavorando altrove.
L'approccio economico riconosce che i costi impliciti, come quelli espliciti, sono reali e incidono sul profitto economico dell'azienda. Tenendo conto dei costi impliciti, è possibile calcolare l'utile economico, che spesso è inferiore all'utile contabile a causa dell'inclusione di questi costi non monetari. Il profitto economico è una misura più completa della redditività, poiché riflette il costo totale delle opportunità sacrificate per produrre un bene o un servizio.
Per massimizzare il proprio profitto economico, un'azienda deve quindi considerare sia i costi espliciti che quelli impliciti, assicurandosi di utilizzare le proprie risorse nel modo più efficiente in relazione a tutte le opzioni disponibili. È questa analisi complessiva che informa le decisioni strategiche e contribuisce a una gestione oculata delle risorse aziendali.
Illustrazione di esempi di costi impliciti[modifier | modifier le wikicode]
I costi impliciti, spesso definiti costi non registrati o costi di opportunità, sono elementi essenziali per valutare la reale redditività di un'azienda. I seguenti esempi illustrano perfettamente la natura dei costi impliciti:
- Il costo del capitale proprio investito nell'azienda: quando un imprenditore investe capitale proprio nella sua azienda, rinuncia all'interesse o al rendimento che avrebbe potuto ottenere investendo questo denaro altrove, ad esempio in un conto di risparmio, in obbligazioni, in azioni o in qualsiasi altra opportunità di investimento. Il costo implicito è il mancato rendimento finanziario. Per un'analisi economica completa, questo costo opportunità deve essere considerato come una spesa reale, perché rappresenta il costo reale del capitale che non è disponibile per altri usi.
- Il salario che l'imprenditore riceverebbe come dipendente in un'altra attività: se l'imprenditore dedica il suo tempo e i suoi sforzi alla sua attività, non può destinarli a un lavoro retribuito altrove. Il costo implicito è quindi il salario che l'imprenditore avrebbe potuto guadagnare lavorando per qualcun altro o impegnandosi in un'altra attività professionale. Questo costo deve essere preso in considerazione quando si valuta la redditività dell'impresa, in quanto rappresenta un reddito potenziale che non è stato realizzato.
Questi costi impliciti sono spesso difficili da quantificare con precisione, in quanto implicano stime su quale potrebbe essere un'alternativa "migliore". Tuttavia, sono fondamentali per le decisioni economiche perché forniscono una misura più realistica della performance economica di un'azienda. Ignorare i costi impliciti potrebbe portare a una valutazione eccessiva della salute e del successo finanziario dell'azienda, in quanto il profitto contabile potrebbe apparire più alto del profitto economico effettivo dopo aver tenuto conto di questi costi. In breve, i costi impliciti svolgono un ruolo fondamentale nel prendere decisioni economiche consapevoli. Aiutano a valutare se le risorse dell'azienda sono utilizzate nel modo più vantaggioso possibile e se l'azienda sta generando un rendimento sufficiente a giustificare questi costi opportunità.
Analisi del commercialista e dell'economista nella valutazione dei costi e dei profitti di un'azienda[modifier | modifier le wikicode]
Il ruolo del commercialista e dell'economista nella valutazione dei costi e dei profitti di un'azienda differisce in modo significativo a causa dei rispettivi approcci ai costi impliciti.
Il contabile si concentra sulle transazioni finanziarie concrete e sui flussi di cassa. Calcola il profitto contabile sottraendo i costi espliciti, che sono i pagamenti monetari effettuati per le operazioni dell'azienda, dal reddito generato dalla vendita di beni o servizi. I costi espliciti sono quindi tutti i costi che provengono direttamente dal flusso di cassa dell'azienda e sono registrati nei libri contabili: stipendi pagati, affitti, costo delle materie prime, interessi sui prestiti, ecc. I costi impliciti, non essendo monetari e non rappresentando un vero e proprio flusso di cassa, non vengono presi in considerazione nei bilanci tradizionali.
Gli economisti, invece, includono nei loro calcoli sia i costi espliciti che quelli impliciti per ottenere il cosiddetto profitto economico. Questo approccio è più ampio perché riconosce che le risorse hanno un valore che va oltre il loro costo monetario diretto. Incorporando i costi di opportunità, l'economista misura il costo reale della produzione e il successo finanziario dell'azienda in termini di massimizzazione del valore piuttosto che di semplice massimizzazione del flusso di cassa. Il profitto economico è quindi definito come ricavi meno la somma dei costi espliciti e dei costi impliciti.
Questa distinzione è fondamentale perché può portare a interpretazioni molto diverse della performance finanziaria di un'azienda. Un utile contabile positivo non significa necessariamente che l'azienda sia economicamente sostenibile se, una volta presi in considerazione i costi impliciti, l'utile economico risulta essere pari a zero o negativo. Di conseguenza, le decisioni basate esclusivamente sui dati contabili possono talvolta essere fuorvianti se non si tiene conto anche dei costi opportunità delle risorse impiegate.
Utile economico e utile contabile[modifier | modifier le wikicode]
La distinzione tra utile economico e utile contabile è fondamentale per l'analisi della performance di un'azienda.
L'utile contabile è il risultato finanziario che rimane dopo aver sottratto i costi espliciti dai ricavi totali. È il dato che di solito viene riportato nei bilanci di un'azienda e quello su cui spesso si basano le decisioni aziendali. È un indicatore della redditività operativa immediata dell'azienda.
L'utile economico, invece, tiene conto dei costi espliciti e impliciti. Il profitto economico si calcola sottraendo dai ricavi totali non solo i costi espliciti, ma anche il valore dei costi opportunità delle risorse utilizzate nel processo produttivo. Questo include elementi come il costo del capitale proprio e il salario alternativo che l'imprenditore potrebbe guadagnare altrove. Il profitto economico è quindi una misura della redditività che riflette l'efficienza complessiva con cui un'azienda utilizza tutte le sue risorse, comprese quelle per cui non riceve un pagamento monetario diretto.
Dato che il profitto economico include costi aggiuntivi che il profitto contabile non include (costi di opportunità), è logico che il profitto economico non possa mai superare il profitto contabile. Se tutti i costi opportunità fossero pari a zero, il profitto economico e quello contabile sarebbero uguali. Tuttavia, nella realtà, ci sono quasi sempre dei costi opportunità, quindi l'utile economico è spesso inferiore all'utile contabile.
È possibile che un'azienda mostri un utile contabile positivo pur avendo un utile economico pari a zero. Ciò può accadere quando i costi opportunità consumati dall'azienda sono esattamente equivalenti all'utile contabile. In questa situazione, sebbene l'azienda appaia redditizia dal punto di vista contabile, dal punto di vista economico sta semplicemente coprendo tutti i suoi costi, compresi i costi di opportunità, senza generare un reale ritorno sulle sue risorse. Si tratta di uno stato di "profitto normale", in cui l'azienda si limita a coprire i suoi costi impliciti ed espliciti, ma non ottiene alcun surplus o guadagno economico reale.
Questo confronto visivo contrappone due metodi di valutazione della performance finanziaria di un'azienda: uno dal punto di vista economico e l'altro dal punto di vista contabile.
Da un lato, il punto di vista economico tiene conto di una visione più ampia della redditività. Questo modello suddivide i ricavi totali in tre segmenti. Partendo dalla base, i costi espliciti sono i pagamenti diretti per risorse quali manodopera, materiali e affitto. A questi si aggiungono i costi impliciti, che rappresentano il valore di ciò a cui l'azienda ha rinunciato utilizzando le proprie risorse nel modo attuale piuttosto che nella migliore alternativa disponibile. Tra questi, ad esempio, il reddito potenziale di un investimento che il capitale dell'azienda avrebbe potuto ottenere altrove, o lo stipendio che un proprietario avrebbe potuto guadagnare lavorando in un'altra azienda. La sezione superiore, colorata di verde, mostra il profitto economico, noto anche come "sovraprofitto". Si tratta dell'importo che rimane dopo che tutti i costi, espliciti e impliciti, sono stati sottratti dai ricavi totali. Questo profitto economico è spesso molto più piccolo di quello contabile, perché tiene conto di una gamma più ampia di costi.
La visione contabile, invece, si concentra esclusivamente sulle transazioni tangibili e sui flussi di cassa. I costi espliciti vengono sottratti dai ricavi totali per determinare il profitto contabile, rappresentato nella parte superiore del grafico. Questo profitto ignora i costi di opportunità e tende quindi a presentare un quadro più ottimistico della salute finanziaria dell'azienda.
Il grafico evidenzia un concetto importante: un utile contabile positivo non significa necessariamente che l'azienda sia economicamente redditizia. È possibile che, anche se un'azienda presenta un utile contabile, abbia un utile economico pari a zero o addirittura negativo una volta presi in considerazione i costi di opportunità. Questo può portare a un fraintendimento della reale performance dell'azienda, perché l'utile contabile sovrastima la redditività dell'azienda ignorando i costi di opportunità.
Questa immagine illustra la necessità per le aziende di prendere in considerazione non solo i costi e i ricavi immediati, ma anche i costi opportunità associati alle loro decisioni economiche. Ciò consente una valutazione più accurata della performance finanziaria e aiuta a garantire che le risorse siano allocate nel modo più efficiente. Per i decisori e gli analisti, questa distinzione è essenziale per fare scelte informate che tengano conto del valore totale che l'azienda crea o potrebbe creare.
La funzione di produzione e i costi totali[modifier | modifier le wikicode]
La funzione di produzione e la funzione dei costi totali sono due concetti strettamente correlati nell'analisi economica della produzione di un'azienda. La funzione di produzione stabilisce un legame tecnico tra le quantità di input utilizzati e la quantità di output prodotti. Essa riflette l'efficienza con cui un'azienda trasforma gli input, come il lavoro, le materie prime e il capitale, in prodotti o servizi finiti. Questa relazione è spesso rappresentata graficamente e può assumere forme diverse a seconda delle tecnologie e dei processi produttivi utilizzati dall'azienda.
La funzione di costo totale, invece, mette in relazione la quantità prodotta con i corrispondenti costi di produzione. I costi di produzione comprendono tutti i costi espliciti e impliciti associati alla produzione di beni o servizi. I costi totali generalmente aumentano con la quantità prodotta, ma non sempre in modo lineare a causa dell'esistenza di costi fissi che non variano con la produzione e di costi variabili che invece variano.
L'interazione tra la funzione di produzione e la funzione di costo totale è fondamentale. I vincoli tecnici della funzione di produzione, come le leggi dei rendimenti decrescenti, hanno un'influenza diretta sui costi totali. Ad esempio, se un'azienda aumenta la quantità di un input, la produzione può inizialmente aumentare a un tasso crescente. Tuttavia, dopo un certo punto, l'aggiunta di altri input può portare a un aumento meno che proporzionale della produzione a causa della saturazione dell'efficienza degli input aggiuntivi.
Gli economisti utilizzano la funzione di costo totale per capire come variano i costi al variare del livello di produzione e per identificare il livello di produzione in cui i costi medi sono minimizzati. Questo è fondamentale per le decisioni sui prezzi e sulla produzione. Identificando il costo marginale di produzione - il costo di produzione di un'unità aggiuntiva - le aziende possono determinare il prezzo di vendita e la quantità di prodotto ottimali per massimizzare i profitti.
Le funzioni di produzione e di costo totale forniscono quindi una panoramica dell'efficienza produttiva e della struttura dei costi di un'azienda. La comprensione della loro interdipendenza è essenziale per l'analisi economica e per la pianificazione strategica di un'azienda.
Questi due grafici distinti rappresentano un concetto diverso dell'economia della produzione.
Il grafico a sinistra descrive una funzione di produzione con la quantità prodotta sull'asse verticale e il numero di lavoratori (che è un input di produzione) sull'asse orizzontale. La curva verde rappresenta la funzione di produzione e mostra come la quantità prodotta aumenti con il numero di lavoratori. La pendenza della curva in un punto specifico è rappresentata dalla PmL, che sta per produttività marginale del lavoro. Si tratta del contributo aggiuntivo alla produzione derivante dall'aggiunta di un'unità di lavoro in più. Inizialmente, la curva mostra che la produttività marginale è in aumento, come indica l'inclinazione verso l'alto della curva di produzione. Tuttavia, quando il numero di lavoratori continua ad aumentare, la curva si appiattisce, indicando una diminuzione della produttività marginale del lavoro. Ciò può essere dovuto alla diminuzione dei rendimenti, in cui l'aggiunta di altri lavoratori porta a un aumento meno che proporzionale della produzione, poiché altri fattori (come i macchinari o il capitale) diventano limitanti.
Il grafico a destra rappresenta la funzione di costo totale con il costo totale sull'asse verticale e la quantità prodotta sull'asse orizzontale. La curva rossa indica che i costi totali aumentano con la quantità prodotta. Inizialmente, la curva sale lentamente, riflettendo i costi fissi che non cambiano con la produzione. Con l'aumento della produzione, la curva diventa più ripida, riflettendo l'aumento dei costi variabili. Il costo totale comprende i costi fissi più i costi variabili moltiplicati per la quantità prodotta. Poiché la curva ha la forma di una J rovesciata, ciò suggerisce che l'azienda sta sperimentando rendimenti di scala crescenti fino a un certo punto, dopodiché sperimenta rendimenti di scala decrescenti.
L'analisi di questi grafici è fondamentale per la gestione aziendale. La funzione di produzione mostra come l'efficienza del lavoro influenzi la quantità di beni o servizi che possono essere prodotti, mentre la funzione di costo totale mostra come questi livelli di produzione si traducano in costi. La comprensione di queste relazioni aiuta le aziende a ottimizzare i livelli di produzione per massimizzare i profitti. Ad esempio, un'azienda potrebbe cercare di produrre a un livello in cui la produttività marginale sia elevata prima che i rendimenti decrescenti inizino a manifestarsi, monitorando al contempo i costi totali per garantire che i costi variabili non inizino a crescere in modo sproporzionato rispetto alla produzione.
Prodotto marginale e medio del lavoro[modifier | modifier le wikicode]
Il prodotto marginale del lavoro (MPL) è un concetto fondamentale in economia che descrive l'impatto aggiuntivo sulla produzione totale dell'aggiunta di un lavoratore in più, assumendo che tutti gli altri fattori di produzione rimangano costanti. È una misura dell'efficienza marginale del lavoro nel processo produttivo.
Matematicamente, per piccoli incrementi, il prodotto marginale del lavoro può essere espresso come il rapporto tra la variazione della quantità prodotta () e la variazione della manodopera (), ottenendo la formula:
Questa formula rappresenta il tasso di variazione della produzione rispetto alla variazione della quantità di lavoro utilizzata, ovvero la pendenza della funzione di produzione sul grafico. In un'analisi più dettagliata e precisa, soprattutto quando siamo interessati a variazioni infinitesimali, il prodotto marginale del lavoro è rappresentato dalla derivata parziale della quantità prodotta rispetto al lavoro, nota come :
Questa derivata parziale fornisce l'esatta pendenza della funzione di produzione in un determinato punto e riflette l'aumento della produzione derivante dall'aggiunta di un'unità infinitesimale di lavoro.
Il concetto di prodotto marginale è fondamentale per capire come le aziende decidono la quantità di lavoro da impiegare. In teoria, un'impresa aumenta la quantità di lavoro fino al punto in cui il prodotto marginale del lavoro è uguale al salario reale, cioè al costo di questa unità di lavoro aggiuntiva. A questo punto, l'impresa massimizza il proprio profitto, perché l'assunzione di un lavoratore in più non produrrebbe una produzione aggiuntiva sufficiente a coprire il costo del suo salario.
In pratica, l'impresa cerca il livello di produzione in cui il costo marginale di produzione (che include il prodotto marginale del lavoro) è uguale al ricavo marginale, al fine di massimizzare i profitti. Tuttavia, vari fattori come i cambiamenti tecnologici, gli aggiustamenti del mercato del lavoro e le normative possono influenzare il prodotto marginale del lavoro e, di conseguenza, la strategia ottimale dell'impresa in materia di lavoro.
La funzione di produzione illustrata suggerisce che il prodotto marginale del lavoro (MPL) è decrescente, il che implica che l'aggiunta di lavoratori supplementari aumenta la produzione, ma in proporzioni sempre minori. Si tratta di una manifestazione del principio dei rendimenti decrescenti, secondo il quale l'efficienza di ogni lavoratore aggiuntivo diminuisce all'aumentare della quantità di lavoro, mantenendo costanti gli altri fattori di produzione.
In termini matematici, ciò significa che la derivata prima della funzione di produzione rispetto al lavoro, , diminuisce all'aumentare di L. Graficamente, la pendenza della curva di produzione, che rappresenta l'AMP, diminuisce man mano che ci si sposta lungo la curva verso destra, indicando che ogni lavoratore aggiuntivo contribuisce meno alla produzione totale rispetto al lavoratore precedente.
Il prodotto medio del lavoro (ALP), invece, è una misura diversa che indica la produzione media per lavoratore. Si calcola dividendo la produzione totale (q) per il numero totale di lavoratori (L), dato dalla formula . Su un grafico della funzione di produzione, il PML è rappresentato dalla pendenza di una semiretta che parte dall'origine e arriva a un punto specifico della curva di produzione. Questo raggio indica la produzione media per tutti i livelli di manodopera impiegati fino a quel punto.
Quando il numero di lavoratori è basso, il LMP può aumentare con l'assunzione di altri lavoratori, che contribuiscono in modo significativo all'aumento della produzione. Tuttavia, in presenza di rendimenti decrescenti, si arriverà a un punto in cui l'aggiunta di nuovi lavoratori inizierà a far diminuire il LMP, perché l'aumento totale della produzione sarà inferiore all'aumento del numero di lavoratori. Questo accade quando il PML è inferiore al PML.
La comprensione di questi indicatori è fondamentale per le aziende quando decidono di assumere nuovi lavoratori. Le aziende cercheranno di bilanciare il costo dell'aggiunta di lavoratori con i benefici della produzione aggiuntiva per massimizzare l'efficienza e la redditività.
Rendimenti decrescenti[modifier | modifier le wikicode]
La legge dei rendimenti marginali decrescenti è un principio fondamentale dell'economia che descrive come, dopo un certo punto, ogni unità aggiuntiva di un fattore di produzione (in questo caso, il lavoro) contribuisca meno alla produzione totale rispetto alla precedente, quando tutti gli altri fattori di produzione sono mantenuti costanti. Si tratta di una legge che ha importanti implicazioni per la produttività e le decisioni sulla produzione.
L'intuizione alla base di questa legge può essere compresa con un semplice esempio: immaginate una cucina con un unico forno e diversi cuochi. Inizialmente, l'aggiunta di altri cuochi può aumentare la produzione di pasti perché c'è abbastanza lavoro per tutti e il forno viene utilizzato in modo ottimale. Tuttavia, una volta raggiunto il numero ottimale di cuochi in cucina, l'aggiunta di altro personale non renderà più veloce la cottura dei pasti perché il forno diventa un collo di bottiglia. I cuochi in più potrebbero addirittura ostacolarsi a vicenda, con una conseguente riduzione dell'efficienza complessiva.
Applicato al contesto più ampio della produzione economica, ciò significa che se un'azienda continua ad aggiungere manodopera a una quantità fissa di altre risorse (come macchinari, edifici o tecnologia), il contributo aggiuntivo di ogni nuovo lavoratore diminuirà. I primi lavoratori possono utilizzare in modo efficiente le macchine e lo spazio a disposizione, ma i lavoratori successivi avranno meno macchine da utilizzare e meno spazio in cui lavorare, riducendo la loro produttività marginale.
Questa legge spiega perché le aziende non possono semplicemente aumentare la produzione all'infinito aggiungendo altri lavoratori. Devono invece trovare un equilibrio tra il numero di lavoratori e la quantità di altre risorse a loro disposizione. Per aumentare la produzione oltre un certo punto, un'azienda dovrà investire in altri fattori produttivi, come l'acquisto di macchinari aggiuntivi o l'ampliamento delle strutture, piuttosto che affidarsi esclusivamente all'aggiunta di manodopera.
Quando i lavoratori si trovano a dover condividere risorse limitate come computer o fotocopiatrici, l'efficienza individuale inizia a diminuire. Questo calo si manifesta inizialmente con piccole inefficienze, come l'attesa per l'utilizzo delle attrezzature, ma può rapidamente degenerare in problemi più significativi di coordinamento e comunicazione quando si aggiungono altri lavoratori. I ritardi si accumulano, i lavoratori passano più tempo ad aspettare che a produrre e la frustrazione può portare a un morale basso, incidendo ulteriormente sulla produttività.
Graficamente, questo si traduce in una funzione di produzione che, dopo un certo punto, si appiattisce all'aumentare della quantità di lavoro, riflettendo una diminuzione della produttività marginale. Ogni lavoratore aggiuntivo aggiunge meno alla produzione totale rispetto al lavoratore che lo ha preceduto. Il grafico della funzione di costo totale rivela l'impatto finanziario di questa legge: all'aumentare della produzione, iniziano a crescere anche i costi marginali, ossia il costo di produzione di un'unità aggiuntiva. Questo perché, se la produzione richiede più manodopera per ogni unità aggiuntiva a causa della congestione delle risorse, il costo di produzione di quell'unità aggiuntiva aumenterà inevitabilmente.
In realtà, le aziende possono incontrare questo problema quando le loro dimensioni raggiungono un punto in cui le risorse iniziano a scarseggiare rispetto al numero di dipendenti. La soluzione per evitare questa trappola non è sempre quella di aggiungere altre risorse, ma può anche comportare una migliore gestione delle risorse esistenti, il miglioramento dei processi di lavoro o l'investimento in tecnologie che migliorino l'efficienza.
L'intuizione alla base della legge dei rendimenti marginali decrescenti e del suo impatto sui costi è che l'efficienza e la redditività possono risentirne se un'azienda non riesce a bilanciare correttamente l'uso del lavoro con le altre risorse a sua disposizione. Ciò sottolinea l'importanza della gestione strategica delle risorse per ottimizzare la produzione e controllare i costi in un determinato ambiente produttivo.
Caso di studio: funzione di produzione e costo totale[modifier | modifier le wikicode]
L'esempio seguente mostra la funzione di produzione e la struttura dei costi di un produttore di pizza in funzione del numero di lavoratori impiegati. Quando la pizzeria non impiega lavoratori, naturalmente non c'è produzione e il costo totale è costituito esclusivamente dai costi fissi del negozio, che ammontano a 30. Questa somma è probabilmente rappresentativa di costi quali l'affitto, le utenze e l'ammortamento delle attrezzature. Questa somma è probabilmente rappresentativa di costi quali l'affitto, le utenze e l'ammortamento delle attrezzature, che sono invariabili indipendentemente dal livello di attività.
Con l'introduzione del primo lavoratore, la produzione inizia a 50 pizze, il che indica un contributo significativo all'attività da parte di questo singolo lavoratore. Il costo totale sale modestamente a 40, incorporando il costo fisso del laboratorio più un costo variabile aggiuntivo di 10 per la manodopera. Questo costo aggiuntivo rappresenta il salario o lo stipendio del lavoratore.
Con l'aggiunta di ogni altro lavoratore, la produzione di pizze aumenta, ma è interessante notare che l'aumento della produzione diminuisce ogni volta, passando da 40 pizze in più con il primo lavoratore a solo 10 pizze in più con il quarto lavoratore. Ciò illustra la legge dei rendimenti marginali decrescenti, per cui ogni lavoratore aggiuntivo contribuisce sempre meno alla produzione complessiva, probabilmente a causa della limitazione delle risorse condivise, come lo spazio di lavoro o le attrezzature della cucina.
Allo stesso tempo, sebbene il costo fisso dell'officina rimanga costante, il costo totale del lavoro aumenta linearmente con l'aggiunta di ogni nuovo lavoratore. Questo aumento lineare è il risultato dell'aggiunta del costo del lavoro per ogni nuovo lavoratore, ipotizzando che ogni lavoratore costi lo stesso importo, indipendentemente dalla produzione realizzata.
Infine, il costo totale di produzione, che è la somma dei costi fissi e variabili, aumenta con ogni aggiunta di lavoratori, riflettendo l'aumento dei costi di produzione. Tuttavia, dato il calo della produttività marginale, aumenta anche il costo di produzione di un'unità aggiuntiva, il che significa che l'azienda deve spendere di più per ogni pizza aggiuntiva prodotta oltre un certo punto. Ciò suggerisce che, sebbene l'aggiunta di manodopera possa aumentare la produzione, lo fa a un costo marginale crescente, un fattore che le imprese devono gestire con attenzione per mantenere la redditività.
Questa analisi evidenzia l'importanza di ottimizzare il numero di lavoratori nella produzione. Un produttore di pizza, o qualsiasi azienda, deve individuare il numero ottimale di lavoratori per massimizzare la produzione senza incorrere in costi sproporzionati dovuti alla diminuzione dei rendimenti marginali. Ciò richiede un'attenta comprensione dei costi fissi e variabili e del loro impatto sul costo totale e sulla redditività dell'azienda.
Questo grafico rappresenta la funzione di produzione che mostra la relazione tra il numero di lavoratori assunti e la quantità di pizze prodotte all'ora da un produttore di pizza. Il grafico mostra una tipica curva di produzione che inizialmente aumenta rapidamente con l'aggiunta di lavoratori, ma inizia ad appiattirsi dopo un certo numero di lavoratori assunti, indicando una diminuzione della produttività marginale.
Inizialmente, con l'aggiunta dei primi lavoratori, l'aumento della produzione è sostanziale per ogni lavoratore aggiuntivo, a dimostrazione di un'elevata produttività marginale. Ciò può essere dovuto a un uso più efficiente delle attrezzature e a una specializzazione del lavoro che consente un aumento significativo della produzione.
Tuttavia, il grafico mostra anche che, dopo l'aggiunta di alcuni lavoratori, la produzione continua a crescere ma a un ritmo più lento. Questo accade perché ogni lavoratore aggiuntivo contribuisce alla produzione complessiva in misura minore rispetto al precedente, un fenomeno che riflette la legge dei rendimenti marginali decrescenti. Questa legge suggerisce che esiste un punto ottimale di lavoro oltre il quale l'efficienza di ogni lavoratore aggiuntivo inizia a diminuire, spesso a causa della condivisione di risorse limitate o della congestione.
Il grafico mostra che l'assunzione del quarto e del quinto lavoratore, ad esempio, aumenta la produzione ma a un tasso decrescente rispetto ai primi lavoratori. Questo può essere interpretato come un segno che lo spazio di lavoro, i forni per la pizza o altre attrezzature stanno diventando un vincolo e che l'aggiunta di altri lavoratori non può essere sfruttata appieno.
Per il produttore di pizza, questo grafico è essenziale per determinare il numero ottimale di lavoratori da assumere per massimizzare la produzione senza incorrere in costi inutili per guadagni marginali di produzione. Analizzando il punto in cui la curva inizia ad appiattirsi, il produttore può identificare il punto di diminuzione dei rendimenti e prendere decisioni informate sulle dimensioni della forza lavoro da mantenere per ottenere un'efficienza ottimale.
La curva del costo totale mostrata nell'immagine rappresenta la relazione tra la quantità prodotta (pizze all'ora) e il costo totale in euro. La curva mostra una progressione verso l'alto che si intensifica all'aumentare della produzione, tipica delle funzioni di costo totale in cui i costi variano con la produzione.
La parte iniziale della curva sale relativamente lentamente, suggerendo che i costi fissi dominano quando la produzione è bassa. I costi fissi sono spese che non cambiano con il livello di produzione, come l'affitto del negozio, il costo delle attrezzature e forse lo stipendio base dei dipendenti. Pertanto, quando il numero di pizze prodotte è basso, l'aumento del costo totale è moderato perché i costi variabili (come gli ingredienti della pizza e il costo marginale del lavoro) sono ancora minimi.
Con l'aumento della produzione, la curva sale più ripidamente. Ciò indica che i costi variabili iniziano ad avere un impatto significativo sui costi totali. I costi variabili possono includere la spesa extra per gli ingredienti, l'energia utilizzata per cuocere più pizze e i salari extra per i lavoratori assunti per aumentare la produzione. Questo aspetto della curva è coerente con la legge dei rendimenti marginali decrescenti: con l'aumento della produzione, i costi marginali della produzione di ogni pizza aggiuntiva aumentano a causa dell'uso meno efficiente delle risorse, man mano che il negozio si avvicina o supera la sua capacità produttiva ottimale.
La forma della curva suggerisce che ogni pizza aggiuntiva costa di più rispetto alla precedente, indicando rendimenti di scala decrescenti in questa fascia di produzione. Questa è una considerazione importante per il produttore di pizza quando pianifica l'espansione della produzione. Se continua ad aumentare la produzione, il costo per unità continuerà a crescere, riducendo i profitti.
Per massimizzare la redditività, il produttore deve trovare il livello di produzione in cui il costo totale per unità prodotta è più basso. Ciò implica il raggiungimento di un equilibrio tra costi fissi e variabili, evitando di produrre oltre il punto in cui i costi marginali iniziano a superare i ricavi marginali. La curva dei costi totali è uno strumento essenziale per identificare questo punto e prendere decisioni consapevoli sulla quantità di produzione.
Diverse misure di costo[modifier | modifier le wikicode]
Diverse misure di costo[modifier | modifier le wikicode]
Costi fissi[modifier | modifier le wikicode]
I costi fissi (FC) rappresentano le spese che un'azienda deve coprire indipendentemente dalla sua produzione. Questi costi rimangono costanti in un determinato periodo anche se la quantità di beni o servizi prodotti varia. I costi fissi sono spesso associati agli investimenti in capitale fisico, come l'acquisto o il noleggio di attrezzature ed edifici, che non cambiano in base alla produzione o alle vendite dell'azienda.
Nel caso di un produttore di pizza, i costi fissi potrebbero includere l'affitto di uno spazio commerciale, l'acquisto o l'ammortamento dei forni per la pizza e delle attrezzature da cucina, gli stipendi dei dipendenti garantiti indipendentemente dal numero di pizze vendute, l'assicurazione e forse alcuni servizi di pubblica utilità come l'acqua o l'abbonamento a Internet. Ad esempio, sia che il produttore di pizza faccia 10 pizze o 100 pizze, l'affitto del locale rimarrà lo stesso per il periodo in questione. Allo stesso modo, l'acquisto di un forno per pizza è un costo iniziale che non cambia, sia che il forno venga utilizzato per cuocere una sola pizza, sia che venga utilizzato in modo continuativo.
È fondamentale per le imprese comprendere e gestire i costi fissi, in quanto costituiscono una parte importante della struttura dei costi totali e possono influenzare le decisioni sui prezzi, sulla strategia di produzione e sulla redditività a lungo termine. Un livello elevato di costi fissi può anche aumentare il rischio finanziario di un'azienda, poiché questi costi devono essere coperti indipendentemente dai ricavi. Le aziende devono quindi generare entrate sufficienti a coprire non solo i costi variabili, ma anche i costi fissi, per evitare perdite.
Costi variabili[modifier | modifier le wikicode]
I costi variabili (VC) nel contesto della produzione di un'azienda sono quelli che fluttuano in base al volume dell'attività o della produzione. A differenza dei costi fissi, che rimangono costanti indipendentemente dal livello di produzione, i costi variabili cambiano direttamente con la quantità di beni o servizi prodotti.
Nell'esempio di un produttore di pizza, i costi variabili comprendono gli ingredienti necessari per la preparazione delle pizze, come la farina, la salsa di pomodoro, il formaggio e i condimenti, nonché il costo dell'energia consumata per far funzionare i forni e le altre attrezzature della cucina. Inoltre, se i lavoratori sono pagati all'ora o al pezzo, anche i loro salari sono costi variabili, poiché la manodopera totale richiesta varia in base al numero di pizze prodotte.
Se il produttore produce più pizze, avrà bisogno di più ingredienti e possibilmente di più ore di lavoro, il che aumenterà i suoi costi variabili. Al contrario, se decide di ridurre la produzione, i suoi costi variabili diminuiranno perché utilizzerà meno ingredienti e meno manodopera.
I costi variabili sono essenziali per la gestione aziendale perché influenzano direttamente il margine di profitto per unità venduta. Una chiara comprensione dei costi variabili è necessaria per stabilire strategie di prezzo efficaci e per prendere decisioni sui livelli di produzione ottimali. Controllando e riducendo i costi variabili, un'azienda può aumentare il proprio margine su ogni prodotto venduto, il che è fondamentale per la redditività complessiva. Allo stesso modo, quando si valuta la redditività di un nuovo prodotto o servizio, un'analisi approfondita dei costi variabili associati è fondamentale per garantire che il prezzo di vendita copra tali costi e contribuisca positivamente al profitto complessivo.
Costo totale[modifier | modifier le wikicode]
Il costo totale (TC) è la somma del costo fisso (FC) e del costo variabile (VC). Questa relazione è fondamentale per comprendere la struttura dei costi di un'azienda ed è espressa matematicamente come segue:
TC = FC + VC
Questa equazione illustra che per ogni livello di produzione, il costo totale è composto da una parte che non cambia, rappresentata dai costi fissi, e da una parte che fluttua con il livello di produzione, rappresentata dai costi variabili. I costi fissi sono spese che devono essere pagate indipendentemente dal volume di produzione, come l'affitto, gli stipendi dei dipendenti fissi, il pagamento dei prestiti e l'ammortamento delle attrezzature. I costi variabili variano in base alla produzione, come le materie prime, le forniture e le ore di lavoro pagate per la produzione.
Ad esempio, se un produttore di pizze ha costi fissi mensili di 2.000 euro per l'affitto, le attrezzature e i salari fissi, e costi variabili di 2 euro per pizza per gli ingredienti e l'energia, il costo totale della produzione di 1.000 pizze sarà calcolato sommando il costo fisso al costo variabile totale per quella produzione:
TC = CF + (CV per pizza × numero di pizze)
CT = 2000 + (2 × 1000)
CT= 2000 + 2000
TC =4000 euro
La comprensione del costo totale è fondamentale per prendere decisioni sui prezzi e sui livelli di produzione. Conoscendo il costo totale, un'azienda può determinare il prezzo di vendita minimo necessario per coprire tutti i costi e generare un profitto. Inoltre, analizzando come varia il costo totale al variare del livello di produzione, le aziende possono identificare il punto di produzione più efficiente e massimizzare la loro redditività.
Costo medio[modifier | modifier le wikicode]
Il costo medio (CA), noto anche come costo unitario, è una misura utilizzata per comprendere il costo di produzione per unità di bene o servizio prodotto. Si ottiene dividendo il costo totale (TC) per la quantità totale prodotta (q). Questa relazione è rappresentata dalla seguente formula:
Poiché il costo totale è la somma dei costi fissi e variabili, il costo medio può anche essere espresso come la somma del costo fisso medio (AFC) e del costo variabile medio (AVC), dove il costo fisso medio è il costo fisso per unità prodotta e il costo variabile medio è il costo variabile per unità prodotta. Pertanto, il costo medio è rappresentato anche dalla formula:
Ciò significa che per ogni unità prodotta viene allocata una parte del costo fisso e una parte del costo variabile. Il costo medio consente alle aziende di determinare il costo di produzione di ogni unità di prodotto, che è fondamentale per stabilire prezzi di vendita adeguati e valutare l'efficienza della produzione.
Ad esempio, se un produttore di pizza ha un costo fisso di 2.000 euro e produce 1.000 pizze, il costo fisso medio per pizza è di 2 euro (2.000 euro / 1.000 pizze). Se il totale dei costi variabili per queste 1.000 pizze è di 2.000 euro, anche il costo variabile medio per pizza è di 2 euro (2.000 euro / 1.000 pizze). Il costo medio per pizza sarebbe quindi di 4 euro (2 euro MVC + 2 euro MVC), prima di prendere in considerazione il margine di profitto.
La comprensione del costo medio è particolarmente importante per la strategia dei prezzi. Se il costo medio è inferiore al prezzo di vendita per unità, l'azienda realizza un profitto su ogni unità venduta. Se il costo medio è superiore al prezzo di vendita, l'azienda subisce una perdita per ogni unità. L'obiettivo è quindi spesso quello di ridurre il costo medio, tagliando i costi o aumentando la produzione per distribuire i costi fissi su un maggior numero di unità, riducendo così il costo fisso medio.
Costo marginale ==[modifier | modifier le wikicode]
Il costo marginale (MC) svolge un ruolo cruciale nell'analisi economica della produzione, in quanto misura l'impatto sul costo totale di un'azienda della produzione di un'unità aggiuntiva di un bene o servizio. È essenzialmente la pendenza della funzione di costo totale in un determinato punto, che rappresenta l'aumento del costo totale per ogni incremento unitario della produzione.
Matematicamente, il costo marginale è definito come il rapporto tra la variazione del costo totale () e la variazione della quantità prodotta (). La formula è la seguente:
Quando si considerano variazioni molto piccole della quantità prodotta, il costo marginale può essere espresso come la derivata del costo totale rispetto alla quantità. Per variazioni infinitesimali, la formula è :
Il costo marginale è particolarmente importante nelle decisioni di produzione e di prezzo. Le aziende cercheranno di produrre fino al punto in cui il costo marginale è uguale al ricavo marginale, che è il ricavo aggiuntivo ottenuto dalla vendita di un'unità supplementare. Questo punto è fondamentale perché corrisponde al livello di produzione in cui i profitti sono massimizzati. Se il costo marginale è inferiore al prezzo di vendita dell'unità aggiuntiva, è vantaggioso per l'azienda aumentare la produzione. Al contrario, se il costo marginale supera il prezzo di vendita, produrre di più ridurrebbe il profitto dell'azienda.
In pratica, l'analisi del costo marginale aiuta le aziende ad adeguare il proprio livello di produzione in risposta ai cambiamenti della domanda di mercato, alle variazioni dei costi dei fattori produttivi o all'introduzione di nuove tecnologie, con l'obiettivo di massimizzare l'efficienza e la redditività.
Esempio[modifier | modifier le wikicode]
Questa tabella illustra i costi di produzione di un produttore di limonata. Mostra la relazione tra il numero di bicchieri di limonata prodotti all'ora e i diversi tipi di costo: costo totale, costo fisso, costo variabile, nonché i relativi costi medi e marginali.
Il costo fisso rimane costante a 3,00 euro, suggerendo che si tratta di costi che non dipendono dal volume di produzione, come l'affitto o l'ammortamento delle attrezzature. Il costo totale parte da 3,00 euro quando non viene prodotto vetro e aumenta con la produzione. La differenza tra il costo totale in ogni fase e il costo fisso dà il costo variabile, che aumenta con il numero di bicchieri prodotti.
I costi fissi medi (AFC) sono calcolati dividendo il costo fisso per il numero di lenti prodotte. Poiché il costo fisso è costante, l'AFC diminuisce all'aumentare del volume di produzione. Al contrario, il costo variabile medio (AVC) si ottiene dividendo il costo variabile totale per il numero di lenti prodotte. Il costo medio totale (TC) rappresenta la somma del MFC e dell'AVC e inizialmente diminuisce prima di aumentare leggermente, suggerendo che potrebbe esistere un intervallo di produzione ottimale in cui i costi medi sono minimizzati.
Il costo marginale (MC) rappresenta il costo di un bicchiere aggiuntivo e si ottiene osservando la variazione del costo totale diviso per la variazione della quantità prodotta. Parte da 0,30 euro e aumenta progressivamente, indicando che ogni bicchiere aggiuntivo costa di più alla produzione rispetto al precedente. Ciò riflette i rendimenti marginali decrescenti, in cui il costo aggiuntivo della produzione aumenta dopo un certo punto perché, ad esempio, le attrezzature vengono utilizzate in modo eccessivo o è necessario assumere più manodopera a un tasso più elevato per mantenere la produzione.
Questa serie di dati consente al produttore di limonata di comprendere la propria struttura dei costi e di prendere decisioni informate sui prezzi e sui livelli di produzione. Ad esempio, identificando il punto in cui il costo totale medio inizia ad aumentare, il produttore può determinare la quantità di produzione più efficiente per massimizzare i profitti. Inoltre, comprendendo il costo marginale, il produttore può decidere quanto sia redditizio continuare ad aumentare la produzione.
Esempio: costo totale[modifier | modifier le wikicode]
Questo grafico mostra una curva di costo totale tracciata rispetto alla quantità di pizze prodotte all'ora. La curva mostra una relazione positiva tra il costo totale e il numero di pizze prodotte, indicando che il costo totale aumenta con la produzione.
Inizialmente, la curva sembra aumentare a un tasso relativamente costante, il che potrebbe indicare che i costi variabili dominano i costi totali dopo la copertura dei costi fissi. Questo è coerente con il comportamento tipico dei costi variabili, che aumentano in proporzione alla quantità prodotta. All'aumentare della produzione, si nota che la pendenza della curva diventa più ripida. Ciò suggerisce che il costo di produzione di ogni pizza aggiuntiva aumenta, il che può essere dovuto a diversi fattori, come la diminuzione dei rendimenti marginali, in cui l'aggiunta di più manodopera o di altre risorse non comporta un aumento proporzionale della produzione.
La pendenza crescente della curva dei costi totali può anche riflettere il fatto che l'azienda ha raggiunto la sua capacità produttiva ottimale e la produzione di ulteriori pizze richiede investimenti sproporzionati in fattori produttivi. Ad esempio, se la capacità del forno è massima, la produzione di pizze aggiuntive potrebbe richiedere l'uso di un forno supplementare o di straordinari per il personale, con un conseguente aumento del costo unitario.
L'analisi di questa curva è essenziale per le decisioni di gestione della produzione. Può aiutare il produttore a identificare il livello di produzione più redditizio e a valutare se i costi attuali sono sostenibili nel lungo periodo. Se l'andamento della curva continua, il produttore potrebbe dover riconsiderare il proprio processo produttivo, investire in attrezzature più efficienti o riadattare la propria strategia di prezzo per garantire che l'aumento dei costi non intacchi i profitti.
Esempio: costo marginale[modifier | modifier le wikicode]
Il costo marginale riflette l'aumento del costo totale dovuto alla produzione di un'unità aggiuntiva di un bene o servizio. In un contesto di produttività decrescente, caratteristica della legge dei rendimenti marginali decrescenti, il costo marginale tende ad aumentare all'aumentare della quantità prodotta. Questo accade perché ogni unità aggiuntiva richiede maggiori input o sforzi per essere prodotta, a causa di vincoli di capacità o della maggiore inefficienza dei fattori di produzione aggiuntivi.
Poiché il costo fisso (FC) rimane costante indipendentemente dal livello di produzione, qualsiasi aumento del costo totale quando viene prodotta un'unità aggiuntiva è dovuto a un aumento del costo variabile (VC). Il costo marginale è quindi una misura diretta della variazione del costo variabile. Matematicamente, può essere espresso come segue:
Ciò implica che il costo marginale è uguale alla pendenza della curva dei costi variabili rispetto alla quantità prodotta. In pratica, ciò significa che se il costo di produzione della prossima pizza (ad esempio) è più alto di quello della pizza precedente, ciò è dovuto all'aumento dei costi variabili, come la manodopera extra richiesta o i costi dei materiali extra sostenuti per mantenere la produzione.
Per le imprese, la comprensione del costo marginale è essenziale per prendere decisioni ottimali in materia di produzione e di prezzi. Produrre oltre il punto in cui il costo marginale inizia a superare il prezzo di vendita può ridurre la redditività. Per questo motivo, le aziende in genere mirano a regolare il proprio livello di produzione per mantenere il costo marginale il più basso possibile, soddisfacendo al contempo la domanda del mercato.
Il grafico mostra una curva lineare ascendente che rappresenta il costo marginale (MC) in funzione della quantità prodotta. L'asse verticale rappresenta i costi in CHF (franchi svizzeri), mentre l'asse orizzontale rappresenta la quantità di beni prodotti.
La linea retta indica che il costo marginale rimane costante per ogni unità aggiuntiva prodotta. Ciò suggerisce che per ogni unità aggiuntiva prodotta, il costo aggiuntivo sostenuto dall'azienda rimane lo stesso. Questo tipo di relazione lineare è tipica di una situazione in cui i costi variabili non aumentano con la produzione, come potrebbe accadere se l'azienda opera in un'area di produzione con rendimenti costanti.
Tuttavia, questa situazione è abbastanza ideale e non è spesso osservata nella realtà su lunghi periodi di produzione o su larga scala, poiché la maggior parte delle aziende si troverà ad affrontare rendimenti marginali decrescenti ad un certo punto. In parole povere, ciò significa che la curva del costo marginale è generalmente a forma di U, inizia con una pendenza negativa, raggiunge un minimo e poi diventa positiva con l'aumento della produzione.
La situazione rappresentata da questo grafico potrebbe verificarsi in un contesto in cui l'azienda dispone di una capacità produttiva sufficiente e di risorse, come materie prime e manodopera, che possono essere facilmente e uniformemente aumentate per incrementare la produzione senza incorrere in significativi costi aggiuntivi.
Per l'azienda, un costo marginale costante significa che la pianificazione della produzione può essere effettuata con un certo grado di prevedibilità in termini di costi. Ciò facilita le decisioni in materia di prezzi e di espansione, poiché la struttura dei costi non varia con l'aumento o la diminuzione della produzione. Tuttavia, l'azienda deve sempre monitorare la situazione per individuare eventuali segnali di cambiamento nell'andamento del costo marginale, poiché gli aumenti potrebbero indicare crescenti inefficienze o imminenti vincoli di capacità.
Esempio: costo medio[modifier | modifier le wikicode]
Il comportamento del costo medio è caratteristico di molte strutture produttive ed è un concetto essenziale in economia. La curva a U del costo medio riflette le diverse fasi della produzione e l'efficienza dei costi.
Nella fase iniziale della produzione, i costi medi tendono a diminuire all'aumentare della quantità prodotta. Ciò è dovuto alla distribuzione dei costi fissi su un numero crescente di unità prodotte. Quando la produzione è bassa, ogni unità prodotta deve sostenere gran parte dei costi fissi, rendendo il costo medio per unità relativamente alto. Tuttavia, quando la produzione aumenta, i costi fissi vengono distribuiti su un numero maggiore di unità, riducendo il costo medio per unità. Questa riduzione continua fino a quando l'azienda non raggiunge le cosiddette economie di scala.
Quando la produzione continua ad aumentare oltre questo punto, l'azienda può incontrare rendimenti di scala decrescenti. Ciò significa che i costi variabili iniziano ad avere un impatto più significativo sui costi totali. I costi variabili medi possono aumentare a causa della diminuzione della produttività marginale dei fattori produttivi aggiuntivi. Ad esempio, l'azienda può essere costretta a pagare gli straordinari ai lavoratori o ad affrontare costi di input più elevati a causa dell'aumento della domanda. Di conseguenza, il costo medio inizia ad aumentare, dando alla curva del costo medio la sua caratteristica forma a U.
Questa forma a U implica che esiste un livello ottimale di produzione in cui il costo medio è ridotto al minimo. Per un'azienda, l'identificazione di questo livello è fondamentale perché massimizza l'efficienza e la redditività. Produrre meno di questo livello significa che l'azienda non sta sfruttando appieno la sua capacità produttiva e le sue economie di scala, mentre produrre di più significa che l'azienda sta affrontando inefficienze crescenti e costi marginali in aumento. Pertanto, capire dove si colloca la propria produzione rispetto a questa curva a U è essenziale per le aziende quando prendono decisioni strategiche sui livelli di produzione e di prezzo.
Il grafico mostra la curva del costo medio (CA) in funzione della quantità prodotta, in franchi svizzeri (CHF). Come previsto, la curva ha una forma a U, che indica che il costo medio per unità inizialmente diminuisce con l'aumento della produzione, raggiunge un punto di minimo e poi inizia a crescere con l'aumento della produzione.
Inizialmente, quando la produzione è molto bassa, il costo medio è elevato a causa della distribuzione dei costi fissi su un numero ridotto di unità. Con l'aumento della produzione, i costi fissi vengono distribuiti su un numero maggiore di unità, facendo diminuire il costo medio per unità. La parte discendente della curva rappresenta le economie di scala ottenute con l'aumento della produzione. È in questa fase che l'azienda diventa più efficiente, riducendo i costi medi.
Il punto più basso della curva corrisponde alla Scala Minima Efficiente (MES), ovvero il livello di produzione in cui il costo medio è minimo. A questo punto, l'azienda opera in modo ottimale, non potendo produrre un'unità aggiuntiva a un costo medio inferiore. Questo è il livello di produzione più efficiente per l'azienda.
Al di là dell'MSE, il costo medio inizia ad aumentare, suggerendo che l'azienda sta affrontando rendimenti marginali decrescenti. Quando la produzione aumenta oltre questo punto, ogni unità aggiuntiva costa di più, in parte a causa dell'aumento del costo medio variabile che potrebbe essere causato dall'esaurimento della capacità produttiva, dalla necessità di investire in attrezzature aggiuntive o più costose, o dall'assunzione di manodopera aggiuntiva a tariffe più elevate.
È fondamentale per un'azienda riconoscere dove si trova la sua EME e cercare di massimizzare la produzione intorno a quel punto per minimizzare i costi medi e massimizzare i profitti. Se un'azienda produce meno della sua EME, non è efficiente come potrebbe. Se produce di più, rischia di aumentare inutilmente i costi, il che potrebbe danneggiare la sua competitività sul mercato.
Costo marginale e costo medio[modifier | modifier le wikicode]
La relazione tra costo marginale (MC) e costo medio (AC) è un aspetto fondamentale della teoria economica della produzione. Il costo marginale è il costo di produzione di un'unità aggiuntiva, mentre il costo medio è il costo totale diviso per il numero di unità prodotte. La loro interazione determina la dinamica della produzione e dei costi di un'azienda.
Il costo marginale svolge un ruolo decisivo nel comportamento del costo medio:
- Quando il costo marginale è inferiore al costo medio, ogni unità aggiuntiva prodotta costa meno del costo medio corrente, con l'effetto di far scendere il costo medio. Questo si verifica tipicamente quando l'azienda aumenta la produzione partendo da un basso livello di output, beneficiando delle economie di scala e dell'ammortamento dei costi fissi su un numero maggiore di unità; * quando il costo marginale è superiore al costo medio, significa che il costo di produzione di ogni unità aggiuntiva è superiore al costo medio attuale, con conseguente aumento del costo medio. Questo può accadere quando l'azienda ha superato il punto di massima efficienza e si trova di fronte a rendimenti marginali decrescenti, in cui l'aumento della produzione comporta un aumento proporzionale dei costi.
Il punto in cui il costo marginale interseca il costo medio è particolarmente significativo. Questo si verifica al minimo del costo medio, che è anche la scala minima di efficienza (MES). Al MERS, l'azienda produce a un livello in cui il costo medio per unità è il più basso possibile. Se la produzione aumenta oltre questo punto, il costo marginale, essendo più alto del costo medio, farà aumentare il costo medio.
In pratica, un'azienda cercherà di produrre a un livello in cui il costo marginale è uguale al costo medio, cioè all'EME, perché è qui che la produzione è più efficiente in termini di costi. Produrre meno dell'EME significa che l'azienda non è efficiente come potrebbe, mentre produrre di più significa che l'azienda sta incontrando inefficienze e aumentando i costi.
Il grafico mostra due curve distinte: la curva del costo marginale (Cm) in rosso e la curva del costo medio (CM) in verde, tracciate rispetto alla quantità prodotta, con il costo espresso in franchi svizzeri (CHF).
La curva del costo medio ha la caratteristica forma a U di cui abbiamo parlato: diminuisce rapidamente all'inizio, riflettendo le economie di scala e l'ammortamento dei costi fissi su un numero crescente di unità. Il punto più basso della curva del costo medio rappresenta la Scala Minima Efficiente (MES), dove il costo medio per unità è al minimo. Dopo questo punto, la curva inizia a salire, suggerendo che i costi medi aumentano all'aumentare della quantità prodotta, probabilmente a causa della diminuzione dei rendimenti marginali e dell'aumento dei costi variabili medi.
La curva dei costi marginali inizia al di sopra della curva dei costi medi e la incrocia proprio in corrispondenza dell'EME. Prima di questo punto di incrocio, il costo marginale è inferiore al costo medio, il che significa che l'aggiunta di ulteriori unità di produzione riduce il costo medio. Dopo il punto di incrocio, il costo marginale diventa più alto del costo medio, indicando che ogni unità aggiuntiva costa più del costo medio, con conseguente aumento del costo medio.
Questo grafico illustra l'importante principio economico secondo cui il costo marginale interseca il costo medio nel suo punto minimo. Ciò significa che l'azienda sta producendo all'EME, il livello di produzione più efficiente in termini di costi. Se la produzione dovesse aumentare oltre questo punto, diventerebbe meno efficiente, come dimostra l'aumento del costo medio.
Per un'azienda, comprendere la relazione tra costo marginale e costo medio è fondamentale per ottimizzare la produzione e massimizzare i profitti. Gestire la produzione in modo da mantenere i costi il più possibile vicini al livello EME può aiutare a garantire che l'azienda operi in modo efficiente e redditizio.
Costo medio (fisso e variabile)[modifier | modifier le wikicode]
Il costo fisso medio (AFC) e il costo variabile medio (AVC) sono due componenti del costo totale medio (ATC). Ciascuna misura una parte diversa dei costi totali per unità prodotta.
Costo fisso medio (AFC): Il costo fisso medio è calcolato dividendo il costo fisso totale (FC) per la quantità di beni prodotti (q). I costi fissi sono costi che non cambiano con la quantità prodotta, come l'affitto, gli stipendi dei dipendenti non direttamente coinvolti nella produzione, l'ammortamento dei macchinari e le assicurazioni. La formula del costo fisso medio è la seguente:
All'aumentare della produzione, l'AMC diminuisce perché i costi fissi sono distribuiti su un numero maggiore di unità. Ad esempio, se l'affitto di un'officina è di 1.000 euro al mese e l'officina produce 100 unità, l'AMC è di 10 euro per unità. Se la produzione raddoppia a 200 unità, il CMF scende a 5 euro per unità.
Costo variabile medio (AVC): il costo variabile medio si ottiene dividendo il costo variabile totale (CV) per la quantità prodotta. I costi variabili variano direttamente con la quantità prodotta e comprendono voci come le materie prime, l'energia consumata nella produzione e i salari dei lavoratori pagati a ore. La formula per il costo variabile medio è:
L'AVC può rimanere costante se i costi per unità di input rimangono invariati all'aumentare della produzione, ma può anche variare in base a diversi fattori, come i risparmi sugli acquisti in blocco o l'esaurimento delle risorse che richiedono input più costosi.
In breve, il costo medio totale, che è la somma dell'FPC e del GPC, fornisce una panoramica del costo unitario per l'intera produzione. La comprensione di questi costi medi consente alle aziende di determinare il prezzo di vendita dei loro prodotti, di pianificare i livelli di produzione e di effettuare analisi di redditività.
Più in generale[modifier | modifier le wikicode]
La produttività marginale è inizialmente crescente (specializzazione dei lavoratori nelle loro mansioni) e poi decrescente (perché i fattori fissi devono essere condivisi da un numero crescente di lavoratori).
Il grafico mostra quattro curve che illustrano la relazione tra i costi di produzione e la quantità prodotta in unità.
- Costi fissi medi (AFC): questa curva grigia mostra che il costo fisso medio diminuisce costantemente all'aumentare della quantità prodotta. Ciò è dovuto al fatto che i costi fissi (come l'affitto, gli stipendi dei dipendenti fissi, ecc.) vengono distribuiti su un numero maggiore di unità, diminuendo così il costo attribuito a ogni unità aggiuntiva.
- Costi variabili medi (AVC): la curva marrone rappresenta i costi variabili medi che, in questo caso, sembrano inizialmente diminuire con l'aumentare della produzione, raggiungendo un punto di minimo e poi aumentando nuovamente. Il punto più basso rappresenta il punto in cui l'azienda beneficia pienamente delle economie di scala sui costi variabili. L'inclinazione verso l'alto della curva suggerisce che, dopo un certo punto, l'azienda inizia a sperimentare rendimenti marginali decrescenti, portando a un aumento dei costi variabili per unità.
- Costo medio (CA): la curva verde indica il costo medio totale, che è la somma del CA e del CA. Segue la classica forma a U, scendendo inizialmente con le economie di scala e poi risalendo a causa dei rendimenti marginali decrescenti. Il punto più basso di questa curva indica l'efficienza produttiva ottimale dell'azienda, dove il costo totale medio per unità è il più basso.
- Costi marginali (MC): La curva rossa traccia il costo marginale, ovvero il costo di produzione di un'unità aggiuntiva. Questa curva inizia al di sotto della curva del costo medio, la incrocia nel punto più basso della curva del costo medio (che è anche la Scala Minima Efficiente o MES) e poi continua a salire. Ciò conferma la regola secondo cui quando il costo marginale è inferiore al costo medio, il costo medio diminuisce, mentre quando il costo marginale è superiore al costo medio, il costo medio aumenta.
Le osservazioni fatte nel grafico supportano i principi economici standard, secondo i quali il costo medio raggiunge un minimo quando il costo marginale è uguale al costo medio. Il grafico mostra anche chiaramente che il costo medio variabile è sempre inferiore al costo marginale dopo il punto in cui i costi medi iniziano a crescere, il che è coerente con l'idea che il costo di produzione di un'unità aggiuntiva sia più alto all'aumentare della produzione. Il grafico indica inoltre che il costo marginale incontra il costo medio in corrispondenza dell'EME, dove il costo medio è più basso, un punto di riferimento importante per le decisioni di produzione e di prezzo.
Proprietà[modifier | modifier le wikicode]
Le tre proprietà seguenti sono principi fondamentali nella teoria economica delle funzioni di costo e hanno implicazioni dirette per la gestione della produzione e la strategia dei prezzi aziendali.
- Costo marginale crescente: la proprietà secondo cui il costo marginale aumenterà con la quantità prodotta è legata alla legge dei rendimenti marginali decrescenti. Ciò significa che, nella maggior parte dei processi produttivi, l'aggiunta di ulteriori unità di input (come il lavoro o il capitale) a un certo punto si tradurrà in un aumento meno che proporzionale della produzione. Ciò può essere dovuto a vincoli di capacità, a inefficienze crescenti o a costi aggiuntivi delle risorse. L'aumento del costo marginale riflette il costo aggiuntivo della produzione di un'unità supplementare, che aumenta all'aumentare della quantità di prodotto.
- Forma a U del costo medio : La forma a U del costo medio deriva dal modo in cui i costi fissi e variabili si comportano al variare della produzione. All'inizio della produzione, i costi medi diminuiscono perché i costi fissi sono distribuiti su un numero crescente di unità. Tuttavia, una volta che la produzione raggiunge e supera l'EME, i costi variabili medi iniziano a pesare di più sul costo totale, portando a un aumento del costo medio. Se il costo marginale fosse sempre decrescente, ciò significherebbe che l'azienda continuerebbe indefinitamente a guadagnare in efficienza con ogni unità aggiuntiva prodotta, il che non è realistico nella maggior parte dei casi a causa di vincoli fisici e pratici.
- Intersezione del costo marginale e medio : Il punto in cui il costo marginale interseca il costo medio è fondamentale perché rappresenta il livello di produzione in cui il costo medio è al minimo - la Scala Minima Efficiente (MES). A questo punto, l'aggiunta di altre unità inizia ad aumentare il costo medio, il che significa che l'azienda perde efficienza oltre questo punto. Questo incrocio è quindi un indicatore per l'azienda che ha raggiunto la sua capacità produttiva più efficiente.
Queste proprietà hanno conseguenze pratiche per le aziende. Per massimizzare la redditività, un'azienda dovrebbe cercare di operare al livello EME, dove può minimizzare i costi medi e quindi massimizzare i profitti. Ciò richiede una comprensione approfondita della struttura dei costi e della capacità produttiva. Inoltre, le aziende devono prestare molta attenzione alla gestione della produzione, in modo da non superare il punto in cui i costi marginali iniziano ad aumentare, il che potrebbe portare a una produzione inefficiente e a perdite.
Riassunto grafico[modifier | modifier le wikicode]
L'immagine seguente è una sintesi grafica che rappresenta le relazioni tra costo marginale (MC), costo medio variabile (AVC), costo medio totale (ATC) e costo variabile (VC(q)), in due contesti diversi: quando i costi fissi (FC) sono nulli e quando i costi fissi sono positivi.
L'immagine visualizzata è una sintesi grafica che rappresenta le relazioni tra costo marginale (MC), costo medio variabile (AVC), costo medio totale (ATC) e costo variabile (VC(q)), in due diversi contesti: quando i costi fissi (FC) sono nulli e quando i costi fissi sono positivi.
In entrambi i grafici, le curve del costo marginale (linea arancione tratteggiata), del costo variabile medio (linea marrone) e del costo totale medio (linea verde) presentano caratteristiche tipiche:
- Quando CF=0:
- La curva del costo medio variabile (AVC) e quella del costo medio totale (ATC) partono dallo stesso punto sull'asse delle ordinate perché non ci sono costi fissi da ammortizzare sulle unità prodotte.
- Le curve AVC e ATC inizialmente diminuiscono, raggiungono un punto di minimo e poi iniziano a crescere, formando la classica curva a U che rappresenta economie e poi diseconomie di scala.
- Il costo marginale (MC) interseca le curve MVC e MTC nel loro punto minimo, che è il punto di inflessione in cui il costo marginale inizia a superare il costo medio variabile e il costo totale, indicando che produrre un'unità aggiuntiva diventa più costoso della media.
- Quando CF>0:
- La curva CVM parte dall'origine perché i costi variabili sono pari a zero quando la produzione è pari a zero.
- La curva CTM parte sopra l'origine al livello di costi fissi positivi, perché anche senza produzione l'azienda deve coprire i costi fissi.
- Come in precedenza, le curve CVM e CTM mostrano una diminuzione dei costi medi con l'aumento iniziale della produzione, seguita da un aumento dopo aver raggiunto un minimo.
- Il costo marginale segue la stessa traiettoria del primo grafico, ma è importante notare che il punto in cui il Cm interseca il CTM è più alto sull'asse dei costi a causa della presenza dei costi fissi.
In entrambi i casi, la posizione in cui il Cm interseca il CVM e il CTM è cruciale per le decisioni sulla produzione. È a questo punto che l'azienda non beneficia più delle economie di scala e deve rivalutare l'aumento della produzione per evitare costosi aumenti dei costi medi.
I grafici illustrano chiaramente l'importanza dei costi fissi nel determinare il costo medio totale e mostrano che le aziende devono prendere in considerazione sia i costi fissi che quelli variabili quando analizzano le loro strutture di costo. Dovrebbero cercare di massimizzare la produzione laddove il costo medio è ridotto al minimo, pur riconoscendo che l'aumento della capacità produttiva può portare a costi più elevati nel lungo periodo se si verificano rendimenti marginali decrescenti.
Esempio numerico[modifier | modifier le wikicode]
L'azienda manifatturiera ha una funzione di costo totale complessa che incorpora termini lineari, quadratici e cubici, oltre a un costo fisso. Per questa azienda, le diverse categorie di costo possono essere riassunte come segue:
- Costo totale (TC(q)): Si tratta della funzione che rappresenta la somma totale dei costi fissi e variabili in funzione della quantità prodotta q. Per l'azienda, il costo totale è dato dalla formula: #Costo fisso (CF): è un costo che non varia con la quantità prodotta ed è qui rappresentato da un valore di 450. #Costo variabile (CV(q)): È la parte del costo totale che varia con la quantità prodotta. La funzione del costo variabile è: #Costo marginale (Cm(q)): È il costo aggiuntivo della produzione di un'unità supplementare. Si ricava prendendo la derivata prima della funzione di costo totale rispetto a q :
- Costo fisso medio (CFM(q)): È il costo fisso ripartito su ogni unità prodotta. Diminuisce all'aumentare della quantità prodotta:
- Costo medio variabile (AVC(q)): È il costo variabile per unità prodotta :
- Costo medio (CM(q)): È il costo totale per unità prodotta, pari alla somma del costo fisso medio e del costo variabile medio:
Queste formule forniscono una panoramica completa della struttura dei costi dell'azienda e sono essenziali per valutare le prestazioni economiche e prendere decisioni strategiche sulla produzione e sui prezzi.
Legame tra la funzione di produzione e i costi[modifier | modifier le wikicode]
La funzione di costo totale può essere vista come un riflesso della funzione di produzione, con un'attenzione particolare agli input e ai costi piuttosto che agli output.
In questa interpretazione :
- Funzione di produzione inversa: per una data quantità di output q e con uno stock fisso di capitale fisico K, la funzione di produzione inversa indica il numero di ore di lavoro L necessarie per produrre q. Ciò si basa sull'ipotesi che la tecnologia di produzione e l'efficienza siano già stabilite.
- Costo salariale e costo variabile (VC): moltiplicando queste ore di lavoro per il salario orario w si ottiene il costo salariale, che in questo caso sarebbe il costo variabile totale, assumendo che il lavoro sia l'unico input variabile. La massa salariale è quindi funzione della quantità prodotta q e dello stock di capitale K: Massa salariale = w ⋅ L (K, q)
- Costo totale (TC): Infine, per ottenere il costo totale, aggiungiamo al costo variabile (massa salariale) il costo fisso, che è il costo generato dal capitale fisico (ad es. ammortamento, affitto, manutenzione): TC (K, q) = w ⋅ L (K, q) + Costo fisso.
Questo modo di concepire le funzioni di costo totale come inversione delle funzioni di produzione è particolarmente utile quando si considera la teoria dell'impresa in un contesto produttivo in cui le decisioni di produzione sono prese sulla base dei costi dei fattori produttivi e dell'efficienza del loro utilizzo. Questo metodo sottolinea l'importanza della gestione delle risorse e la necessità di ottimizzare i fattori produttivi per minimizzare i costi e massimizzare i profitti.
Questi due grafici illustrano la relazione tra la quantità di lavoro richiesta e i costi variabili per produrre diverse quantità di un bene in una funzione di produzione di breve periodo con uno stock di capitale fisso (K).
- Grafico della funzione lavoro: nel primo grafico (a sinistra), l'asse verticale (L) rappresenta la quantità di lavoro richiesta e l'asse orizzontale (q) rappresenta la quantità di bene prodotto. La curva mostra le fasi di rendimento crescente e decrescente del lavoro. Inizialmente, all'aumentare della quantità prodotta, è necessaria meno manodopera per ogni unità aggiuntiva prodotta, il che è caratteristico dei rendimenti crescenti. Tuttavia, dopo aver raggiunto un certo livello di produzione (punto di inflessione), la quantità di lavoro richiesta per produrre ogni unità aggiuntiva inizia ad aumentare, indicando rendimenti decrescenti.
- Grafico della funzione di costo variabile: nel secondo grafico (a destra), l'asse verticale rappresenta il costo variabile totale (VC) e l'asse orizzontale rappresenta anche la quantità del bene prodotto. La curva mostra il costo variabile di produzione associato a ciascun livello di produzione. Il costo variabile è calcolato moltiplicando la quantità di manodopera (L) per il salario orario (w), che dà il costo del lavoro. Questa curva riflette la forma della curva del lavoro, dove i costi variabili per unità inizialmente diminuiscono a causa dei rendimenti crescenti, ma poi aumentano a causa dei rendimenti decrescenti del lavoro.
I due grafici illustrano come la funzione di produzione possa essere "invertita" per determinare i costi variabili associati alla produzione di diversi livelli di output. Il concetto di rendimenti decrescenti è fondamentale per capire perché, dopo un certo punto, produrre di più diventa sempre più costoso per l'azienda. Questa informazione è fondamentale per la pianificazione della produzione e per la definizione delle strategie di prezzo, in quanto aiuta a identificare il punto di produzione più efficiente e redditizio.
In pratica, questa analisi può aiutare le aziende a decidere quanti lavoratori assumere e quanto produrre per minimizzare i costi e massimizzare i profitti. Le aziende devono fare attenzione a non produrre oltre il punto in cui i costi marginali superano i costi medi, poiché ciò potrebbe ridurre i profitti complessivi.
Questo grafico illustra la struttura dei costi di un'azienda, evidenziando come si compongono i costi totali e come si evolvono con la quantità prodotta.
Il grafico presenta due curve principali:
- La curva dei costi variabili (CV(q, K)): Questa curva mostra come i costi variabili cambiano con la quantità prodotta (q). La curva inizia nell'origine, indicando che non ci sono costi variabili se la produzione è pari a zero. La curva dapprima sale meno ripidamente, poi diventa più ripida, indicando prima un aumento e poi una diminuzione dei rendimenti del lavoro. Ciò significa che per ogni unità aggiuntiva prodotta, il costo variabile aumenta inizialmente a un tasso decrescente (efficienza crescente), poi a un tasso crescente (efficienza decrescente) a causa della legge dei rendimenti marginali decrescenti.
- La curva del costo totale (CT(q, K)) : Il costo totale è rappresentato dalla somma verticale dei costi fissi (FC) e dei costi variabili (VC). La curva di costo totale inizia dai costi fissi, perché anche senza produzione l'azienda deve sostenere questi costi. La curva TC ha la stessa forma della curva CV, ma è spostata verso l'alto dal valore dei costi fissi.
I costi fissi (FC) sono rappresentati da una linea orizzontale, il che è logico in quanto i costi fissi non cambiano indipendentemente dalla quantità prodotta. Il punto in cui la curva dei costi variabili cambia pendenza (il punto di decrescita) è anche il punto in cui la curva dei costi totali cambia pendenza. Questo punto è cruciale perché indica la quantità di produzione in cui l'efficienza inizia a diminuire.
Il grafico illustra anche che il costo totale per ogni livello di produzione è sempre superiore ai costi variabili a causa dell'aggiunta dei costi fissi. Ciò sottolinea l'importanza per le aziende di coprire non solo i costi variabili, ma anche i costi fissi, al fine di raggiungere la redditività. In sintesi, il grafico è uno strumento utile per visualizzare i costi di produzione e capire come cambia l'efficienza produttiva all'aumentare della quantità prodotta. Per le aziende, la comprensione di queste relazioni è fondamentale per ottimizzare la produzione, stabilire i prezzi e massimizzare i profitti.
Breve e lungo termine[modifier | modifier le wikicode]
La funzione di produzione a breve e a lungo termine[modifier | modifier le wikicode]
In economia è necessario distinguere tra la nozione di produzione a breve e a lungo termine. Nel quadro di breve termine, almeno uno dei fattori di produzione è fisso, spesso il capitale (K), mentre gli altri fattori, come il lavoro (L), possono variare. Ciò riflette situazioni in cui l'azienda può modificare rapidamente la quantità di manodopera impiegata, ma non può cambiare altrettanto facilmente la propria capacità di capitale a causa di impegni a lungo termine, tempi di consegna di nuovi macchinari o semplicemente perché gli adeguamenti del capitale richiedono importanti investimenti e decisioni strategiche.
In un quadro di lungo periodo, il presupposto cambia: tutti i fattori di produzione, compreso il capitale, sono considerati variabili. Ciò consente all'azienda di adattare tutte le sue risorse per trovare la combinazione più redditizia che massimizzi il profitto. La differenza fondamentale tra l'analisi a breve e a lungo termine è la flessibilità con cui l'azienda può regolare tutti i suoi fattori produttivi.
Analisi a lungo termine:
- Scelta della produzione: nel lungo periodo, l'impresa ha la flessibilità di regolare la quantità di capitale fisico (K) e la quantità di lavoro (L) per produrre un determinato livello di output (q). Ciò significa che l'impresa può scegliere tra un insieme più ampio di combinazioni produttive per minimizzare i costi o massimizzare la produzione.
- Isoquanti : L'impresa può utilizzare i grafici degli isoquanti per illustrare le diverse combinazioni di capitale e lavoro che producono lo stesso livello di output. Ogni isoquanto corrisponde a un diverso livello di produzione e la pendenza dell'isoquanto (tasso marginale di sostituzione tecnica) indica il tasso al quale il lavoro può sostituire il capitale mantenendo costante la produzione.
- Massimizzazione del profitto : La massimizzazione del profitto implica la scelta del punto dell'isoquanto in cui il costo di produzione è più basso o, in altre parole, in cui l'isoquanto è tangente alla retta di isocosto. La linea di isocosto mostra tutte le combinazioni di capitale e lavoro che l'azienda può permettersi per un determinato costo totale. L'azienda modificherà la propria combinazione di capitale e lavoro fino a quando il tasso marginale di sostituzione tecnica tra lavoro e capitale sarà uguale al rapporto tra i prezzi di questi fattori.
- Cambiamento di scala: nel lungo periodo, l'azienda può anche effettuare cambiamenti di scala aumentando proporzionalmente tutti i suoi input. Se la produzione aumenta in modo più che proporzionale rispetto agli input, si parla di rendimenti di scala crescenti. Se la produzione aumenta in modo meno che proporzionale, si parla di rendimenti di scala decrescenti. Se aumenta nella stessa proporzione, si parla di rendimenti di scala costanti.
L'analisi a lungo termine è essenziale per la pianificazione strategica e gli investimenti, in quanto consente all'azienda di posizionarsi in modo ottimale per la crescita futura e la competitività sul mercato. Considera l'intero processo produttivo, tenendo conto di come le decisioni di investimento e gli aggiustamenti di capacità influiscono su costi e profitti.
La distinzione tra orizzonti temporali a breve e a lungo termine nella teoria economica è fondamentale per comprendere le decisioni di produzione delle imprese.
Breve termine: nel contesto di breve termine, le imprese considerano fisse alcune risorse, in particolare il capitale fisico. Queste risorse comprendono edifici, macchinari e altre attrezzature che non possono essere modificate rapidamente o senza costi significativi. La funzione di produzione di breve periodo, denominata , riflette questo vincolo: il capitale è una quantità data, mentre il lavoro L può variare. I costi fissi in questo periodo includono le spese legate al capitale, come il pagamento di affitti o prestiti, che non cambiano indipendentemente dal livello di produzione. I costi variabili, invece, comprendono voci come la manodopera e le materie prime, che possono essere modificate in base alla quantità prodotta.
Lungo termine: nel lungo termine, l'azienda può regolare tutti i suoi input, compreso il capitale. Questo le dà la flessibilità di ridimensionare o ristrutturare completamente le sue attività in risposta ai cambiamenti della domanda, alle innovazioni tecnologiche o ad altri fattori esterni. La funzione di produzione di lungo periodo, espressa come , mostra che l'impresa può scegliere la quantità di capitale K e di lavoro L da utilizzare per la produzione. A questo punto, la distinzione tra costi fissi e variabili diventa meno rilevante, poiché tutti i costi sono considerati variabili nel lungo periodo.
La capacità di un'azienda di passare dalla produzione a breve termine alla pianificazione a lungo termine è fondamentale per la sua redditività e crescita a lungo termine. Le decisioni a lungo termine possono comprendere l'investimento in nuove attrezzature, l'espansione o il ridimensionamento degli impianti, o la modifica del modello aziendale per esplorare nuovi mercati o prodotti. Comprendendo e pianificando entrambi gli orizzonti, le aziende possono navigare meglio nelle condizioni di mercato e mantenere la loro competitività nel lungo periodo.
Costi di produzione nel breve e nel lungo termine[modifier | modifier le wikicode]
La distinzione tra costi fissi e variabili è essenziale per comprendere il processo decisionale di un'azienda in termini di produzione e di investimenti su diversi orizzonti temporali.
Breve termine: nel breve termine, alcune spese non possono essere modificate rapidamente o senza costi significativi. Queste spese, come i canoni di leasing o i prestiti per le attrezzature, sono considerate costi fissi perché non cambiano con il livello di produzione. Il capitale fisico, in questo contesto, è spesso un costo fisso perché l'azienda non può facilmente acquisire o cedere i principali beni strumentali per adeguare la produzione nel breve periodo. I costi variabili, invece, possono essere modificati più facilmente e comprendono voci come le materie prime e le ore di manodopera diretta, che variano direttamente con la quantità prodotta.
A lungo termine: nel lungo periodo, l'azienda ha la flessibilità di modificare tutte le sue capacità produttive, compreso il capitale fisico. Ciò significa che i costi che erano fissi nel breve periodo diventano variabili nel lungo periodo. Se si dispone di tempo sufficiente, le aziende possono effettuare investimenti strategici o disinvestimenti per aumentare o diminuire la propria capacità produttiva. Ciò include l'acquisto di nuove attrezzature, l'espansione degli impianti o addirittura la chiusura di parti dell'azienda. Queste decisioni sono guidate da considerazioni sui costi a lungo termine, con l'obiettivo di allineare la capacità produttiva alla domanda prevista e alla strategia complessiva dell'azienda.
La capacità di rendere variabili i costi fissi è fondamentale per la pianificazione strategica e la competitività a lungo termine. Consente alle aziende di adattarsi ai cambiamenti dell'ambiente in cui operano, come le fluttuazioni della domanda, i progressi tecnologici e le modifiche normative. Comprendendo questi concetti, le aziende possono prevedere meglio i loro costi e benefici potenziali e adattare di conseguenza le loro strategie per mantenere una crescita e una redditività sostenibili.
La natura delle funzioni di costo delle aziende varia notevolmente tra il breve e il lungo periodo, a causa della flessibilità di adattamento dei fattori di produzione.
Nel breve periodo, l'azienda opera con fattori fissi, il che significa che deve ottimizzare la produzione regolando solo i fattori variabili. La funzione di costo di breve periodo è vincolata da questi fattori fissi (come attrezzature e impianti) che non possono essere modificati rapidamente o facilmente. Di conseguenza, l'azienda potrebbe non essere in grado di raggiungere il livello di produzione economicamente più efficiente se la domanda cambia rapidamente.
Nel lungo periodo, invece, tutti i fattori diventano variabili. L'azienda può investire in nuove tecnologie, aumentare o ridurre le dimensioni dei suoi impianti e adattare la forza lavoro in modo da soddisfare esattamente le sue esigenze di produzione. Questa flessibilità permette all'azienda di raggiungere livelli di efficienza che il quadro di breve termine non consente. La funzione di costo a lungo termine offre quindi una visione più fluida e dinamica, che riflette la capacità dell'azienda di adattarsi ai cambiamenti del mercato e di ottimizzare i costi di produzione.
Ciò implica che, in teoria, i costi di produzione dovrebbero essere più bassi nel lungo periodo perché l'azienda può realizzare economie di scala e beneficiare di migliori tecnologie o metodi di produzione. Tuttavia, ciò dipende anche dalla capacità dell'azienda di gestire efficacemente questi cambiamenti e di investire saggiamente in modo da ridurre i costi a lungo termine. Inoltre, gli investimenti a lungo termine sono spesso accompagnati da rischi e incertezze che possono influenzare i costi.
L'analisi dei costi a lungo termine è quindi un elemento chiave della strategia aziendale, che richiede un'attenta pianificazione e valutazione delle opportunità di investimento, nonché delle condizioni di mercato che possono influenzare la domanda dei prodotti dell'azienda.
Costi medi nel breve e nel lungo periodo[modifier | modifier le wikicode]
I costi medi, sia a breve che a lungo termine, svolgono un ruolo fondamentale nella pianificazione finanziaria e nella strategia di un'azienda. Tuttavia, essi variano a seconda del periodo considerato, a causa della natura dei costi fissi e variabili.
Costi medi a breve termine: nel breve termine, alcuni costi sono considerati fissi. Ciò significa che, indipendentemente dal livello di produzione, questi costi non cambiano. Ne sono un esempio l'affitto, gli stipendi dei dipendenti fissi e i pagamenti delle attrezzature. I costi medi di breve periodo (SRA) sono quindi influenzati dalla quantità di produzione:
- Se la produzione è bassa, i costi fissi medi (CFA) sono alti perché sono distribuiti su un numero ridotto di unità; con l'aumento della produzione, i CFA per unità diminuiscono perché sono distribuiti su un numero maggiore di unità; i costi variabili medi (CVA) cambiano con la produzione, ma in misura minore rispetto ai costi fissi; i costi totali medi di breve periodo (SRAC) inizialmente diminuiscono con l'aumento della produzione (sfruttando le economie di scala), ma possono aumentare dopo aver raggiunto il punto di diminuzione dei rendimenti marginali.
Costo medio di lungo periodo: nel lungo periodo, tutti i costi sono considerati variabili. Un'azienda può adattare la propria capacità produttiva modificando la quantità di capitale fisico e di lavoro utilizzati. I costi medi di lungo periodo (LRAAC) offrono una prospettiva più flessibile:
- Le economie di scala possono essere ottenute aumentando la produzione, il che riduce il costo medio di lungo periodo fino a un certo punto.
- I rendimenti di scala costanti si verificano quando l'aumento dei fattori produttivi porta a un aumento proporzionale della produzione, mantenendo così costante il costo medio.
- I rendimenti di scala decrescenti si verificano quando l'aumento dei fattori produttivi porta a un aumento meno che proporzionale della produzione, aumentando così il costo medio.
La curva del costo medio di lungo periodo (LRAEC) è spesso rappresentata come l'inviluppo delle varie curve del costo medio di breve periodo (SRAEC) per vari livelli di capacità produttiva. Essa mostra il costo medio minimo possibile per ogni livello di produzione se l'azienda ottimizza completamente tutti i suoi input.
In pratica, le aziende cercano di produrre dove il costo medio di lungo periodo è più basso, in quanto indica il punto di produzione più efficiente e redditizio. È qui che un'azienda può massimizzare i profitti, in quanto produce al costo medio più basso possibile, pur avendo la flessibilità di adattarsi alle variazioni della domanda nel lungo periodo.
Il grafico mostra un'analisi comparativa dei costi medi a breve e lungo termine di un'azienda in funzione della quantità di produzione. Nel breve periodo, si osservano tre curve distinte che rappresentano i costi medi per impianti di dimensioni diverse: piccoli, medi e grandi. Ogni curva mostra un costo medio che diminuisce con l'aumentare della produzione fino a un certo punto, riflettendo le economie di scala ottenute quando i costi fissi sono distribuiti su un numero crescente di unità prodotte. Tuttavia, dopo aver raggiunto il punto più basso, i costi medi iniziano a salire di nuovo, illustrando i rendimenti marginali decrescenti in cui si sostengono costi aggiuntivi per ogni unità prodotta in più, spesso a causa del sovrautilizzo della capacità esistente o di una maggiore inefficienza.
La curva dei costi medi di breve periodo per l'impianto piccolo raggiunge il suo minimo a un livello di produzione relativamente basso, indicando che piccole quantità di produzione sono ottimali per questa configurazione. L'impianto medio, con una capacità maggiore, raggiunge il punto di costo medio più basso a un livello di produzione più elevato, suggerendo che può produrre in modo più efficiente una quantità maggiore prima di incontrare rendimenti marginali decrescenti. Il grande impianto, con la maggiore capacità, ha il costo medio più basso a un livello di produzione ancora più alto, indicando che è meglio equipaggiato per sfruttare le economie di scala su larga scala.
Al contrario, la curva in rosso, che rappresenta i costi medi a lungo termine, è una curva di inviluppo che si trova al di sotto di tutte le curve dei costi medi a breve termine. Questa curva di inviluppo riflette la flessibilità dell'azienda nell'adattare le dimensioni dell'impianto e nell'ottimizzare altri fattori di produzione su un periodo più lungo. Mostra il costo medio più basso raggiungibile a ciascun livello di produzione se l'azienda adegua perfettamente la propria capacità produttiva alle quantità desiderate. Anche questa curva raggiunge un minimo, indicando il punto di produzione più efficiente nel lungo periodo, ma a differenza delle curve a breve termine, offre una prospettiva più ampia delle opzioni di ottimizzazione disponibili per l'azienda, compresa la possibilità di scegliere tra diverse dimensioni di impianto.
L'analisi rappresentata in questo grafico evidenzia che le aziende tendono ad avere una maggiore flessibilità e costi potenzialmente più bassi nel lungo periodo, in quanto possono regolare tutti i fattori di produzione, compreso il capitale. Le decisioni prese oggi con impegni a lungo termine possono definire la traiettoria futura dei costi di produzione e, di conseguenza, influenzare la competitività e la redditività di un'azienda. Le aziende devono quindi valutare attentamente le loro decisioni in materia di investimenti e capacità produttiva, tenendo conto delle previsioni della domanda e degli sviluppi tecnologici, per garantire che possano produrre al livello più efficiente e redditizio possibile.
Economie di scala[modifier | modifier le wikicode]
Le economie di scala si riferiscono alla riduzione dei costi medi di lungo periodo quando un'azienda aumenta la propria produzione. La pendenza della funzione del costo medio di lungo periodo (LRAC) è un indicatore chiave della presenza di economie di scala.
Se la pendenza della funzione LRAC è negativa, significa che i costi medi diminuiscono all'aumentare della quantità prodotta. Questo è il classico segnale di economie di scala: produrre di più diventa meno costoso per unità grazie a una maggiore efficienza, all'ammortamento dei costi fissi su una maggiore produzione o all'acquisizione di fattori produttivi a costi inferiori attraverso acquisti in quantità.
Quando la pendenza della funzione CMLT diventa positiva, indica diseconomie di scala. Ciò può verificarsi quando l'aumento della produzione porta a un aumento dei costi medi, forse a causa di una maggiore complessità gestionale, dell'esaurimento dei benefici dell'efficienza o di vincoli operativi.
Infine, se la pendenza della funzione CMLT è pari a zero, significa che l'azienda sta sperimentando rendimenti di scala costanti. In questo caso, i costi medi non cambiano all'aumentare della produzione. Ogni unità aggiuntiva ha lo stesso costo di produzione, il che indica una proporzionalità diretta tra costi e produzione.
Per i responsabili delle decisioni è fondamentale capire in che posizione si trova l'azienda rispetto a queste diverse fasi delle economie di scala. Ciò consente loro di pianificare espansioni o adeguamenti della capacità produttiva con la consapevolezza di come tali cambiamenti influiranno sui costi e sulla competitività sul mercato. Le economie di scala sono spesso una forza trainante delle strategie di crescita delle aziende, in quanto possono portare a un significativo vantaggio competitivo.
Questo grafico illustra i concetti di economie di scala, rendimenti costanti di scala e diseconomie di scala attraverso la relazione tra costi medi e quantità di produzione.
Nel grafico si possono individuare tre fasi:
- Economie di scala: sul lato sinistro del grafico, la curva del costo medio (AC) è decrescente, a indicare che l'aumento della produzione porta a una diminuzione dei costi medi per unità. Ciò è generalmente dovuto alla distribuzione più efficiente dei costi fissi su un numero crescente di unità prodotte e a una maggiore efficienza nell'uso delle risorse. Le aziende spesso beneficiano delle economie di scala quando sono in fase di crescita o quando possono acquistare i fattori di produzione a prezzi ridotti attraverso ordini in blocco.
- Rendimenti di scala costanti: Al centro del grafico, la curva CM si stabilizza e il costo medio per unità rimane costante nonostante l'aumento della produzione. Ciò suggerisce che l'azienda ha raggiunto un livello di produzione in cui i benefici delle economie di scala sono stati pienamente realizzati e qualsiasi ulteriore aumento della produzione non modifica il costo medio. Questo può verificarsi in situazioni in cui l'azienda opera alla sua capacità ottimale.
- Diseconomie di scala: sul lato destro del grafico, la curva CM inizia a salire, indicando che i costi medi per unità aumentano con l'aumento della produzione. Questo può essere il risultato di un sovraccarico della capacità produttiva, di costi di gestione aggiuntivi o di una maggiore complessità operativa che rende la produzione meno efficiente all'aumentare della scala.
I punti neri sulle curve indicano probabilmente i punti minimi dei costi medi per impianti di dimensioni diverse, suggerendo che ogni tipo di impianto ha una quantità ottimale di produzione. Lo spostamento da una curva all'altra riflette le variazioni della capacità produttiva che potrebbero essere ottenute con investimenti a lungo termine, consentendo all'azienda di passare a un livello più elevato di produzione efficiente con un costo medio inferiore.
Questo grafico è uno strumento prezioso per prendere decisioni sugli investimenti e sulla capacità produttiva. Evidenzia l'importanza per le aziende di capire non solo dove si trovano attualmente sulla curva dei costi medi, ma anche di prevedere come le variazioni della capacità produttiva possano influire sui loro costi in futuro. Le aziende dovrebbero puntare a operare dove possono ridurre al minimo i costi medi per massimizzare i profitti, pur rimanendo attente ai rischi delle diseconomie di scala.
Rendimenti marginali vs. rendimenti di scala[modifier | modifier le wikicode]
Rendimenti marginali e rendimenti di scala[modifier | modifier le wikicode]
È fondamentale non confondere il rendimento marginale con i rendimenti di scala, poiché si applicano a contesti diversi e hanno implicazioni distinte per le decisioni sulla produzione.
Il rendimento marginale, spesso associato alla legge dei rendimenti marginali decrescenti, si riferisce all'impatto dell'aggiunta di un'unità in più di un singolo fattore di produzione, mantenendo costanti tutti gli altri fattori. Si tratta di un'osservazione a breve termine perché esamina l'effetto immediato e diretto dell'aumento di un singolo fattore di produzione sulla produzione totale. In pratica, ciò può essere illustrato aggiungendo un lavoratore in più a una fabbrica in cui le attrezzature e lo spazio sono vincoli fissi. Inizialmente, l'aggiunta di lavoratori può aumentare significativamente la produzione, ma man mano che se ne aggiungono altri, ognuno di essi contribuirà sempre meno alla produzione totale a causa dei vincoli di spazio e di attrezzature.
I rendimenti di scala, invece, esaminano come la variazione proporzionale di tutti i fattori produttivi influisca sulla produzione. Questo riflette una prospettiva a lungo termine in cui l'azienda ha la possibilità di modificare la propria struttura produttiva, comprese le dimensioni degli impianti, la quantità di macchinari e il numero di dipendenti. Le economie di scala si verificano quando il raddoppio di tutti gli input aumenta la produzione di oltre il doppio. I rendimenti di scala costanti significano che la produzione aumenta nella stessa proporzione dei fattori produttivi, mentre i rendimenti di scala decrescenti si verificano quando la produzione aumenta in misura inferiore alla proporzione in cui aumentano i fattori produttivi.
La comprensione di queste differenze è fondamentale per le aziende quando prendono decisioni strategiche. Nel breve termine, l'ottimizzazione dei costi può comportare la regolazione fine degli input variabili per ottenere il miglior rendimento marginale. A lungo termine, l'azienda deve prendere in considerazione gli investimenti che possono modificare la struttura complessiva dei costi e la capacità produttiva, influenzando così i rendimenti di scala. Queste decisioni strategiche a lungo termine sono essenziali per una crescita sostenibile e per la competitività del mercato.
rendimenti di scala crescenti ==[modifier | modifier le wikicode]
Le economie di scala, spesso associate ai rendimenti crescenti di scala, sono un fenomeno che si osserva quando le aziende aumentano la loro produzione e di conseguenza vedono diminuire i loro costi medi. Questo concetto è radicato in diversi aspetti operativi e organizzativi di un'azienda che si espande. In una grande fabbrica, ad esempio, è possibile combinare diversi compiti che, in strutture più piccole, sarebbero dispersi e gestiti in modo meno efficiente. Questo consolidamento dei compiti può portare a significativi guadagni di efficienza.
Inoltre, un impianto di grandi dimensioni offre l'opportunità di una maggiore specializzazione della manodopera e del capitale. I lavoratori possono concentrarsi su compiti specifici, affinando le loro abilità e competenze attraverso la ripetizione e la concentrazione su un particolare aspetto del processo produttivo. Questa specializzazione può portare a un aumento della produttività per lavoratore. Allo stesso tempo, anche il capitale può diventare più specializzato. Le attrezzature e i macchinari progettati per funzioni specifiche possono essere utilizzati al meglio, aumentando la produttività del capitale.
Un altro vantaggio della produzione su larga scala è la possibilità per un'azienda di investire in manodopera altamente qualificata e in tecnologie avanzate. Mentre questi investimenti possono essere costosi e non giustificati per un'attività di piccole dimensioni, un'azienda che opera su larga scala può distribuire questi costi su una produzione più ampia, riducendo così i costi medi. Inoltre, le aziende più grandi possono spesso ottenere prezzi migliori per i loro acquisti grazie agli ordini in blocco e hanno una maggiore capacità di investire in ricerca e sviluppo, che può portare a innovazioni che riducono ulteriormente i costi nel lungo periodo.
Tuttavia, è fondamentale tenere presente che questi vantaggi non sono illimitati. Quando le aziende diventano troppo grandi, possono andare incontro a diseconomie di scala, come difficoltà di gestione, problemi di comunicazione e un coordinamento meno efficace, che in ultima analisi possono portare a costi medi più elevati. Pertanto, sebbene le economie di scala possano offrire notevoli vantaggi, le aziende devono valutare attentamente fino a che punto possono crescere prima che i costi operativi e di gestione aggiuntivi inizino a superare i benefici di una produzione su larga scala.
rendimenti decrescenti di scala =[modifier | modifier le wikicode]
Le diseconomie di scala si verificano quando, a differenza delle economie di scala, i costi medi di un'azienda aumentano all'aumentare della quantità di produzione. Questo fenomeno è generalmente associato alla diminuzione dei rendimenti di scala e può essere attribuito a diversi fattori legati alla crescita dell'azienda.
Quando un impianto raggiunge e supera una certa dimensione, l'integrazione e il coordinamento delle attività possono diventare sempre più complessi. Gestire efficacemente una grande forza lavoro e armonizzare numerose linee di produzione può rivelarsi problematico. Queste difficoltà operative possono portare a un aumento delle inefficienze, poiché la comunicazione diventa più complicata e i processi più soggetti a errori. Di conseguenza, i vantaggi derivanti dall'aumento delle dimensioni possono essere superati, se non addirittura annullati, da queste nuove sfide.
Anche la motivazione e l'impegno dei dipendenti possono essere influenzati da una grande azienda. In strutture più piccole, i dipendenti possono sentirsi più coinvolti e avere una chiara comprensione dell'impatto del loro lavoro sui risultati dell'azienda. Tuttavia, in un ambiente di grandi dimensioni, il senso del contributo personale può diminuire, con conseguente riduzione della produttività e dell'efficacia complessiva.
Inoltre, i sistemi di gestione possono non evolvere allo stesso ritmo delle dimensioni dell'azienda. Le strutture di gestione che funzionavano bene in una piccola o media impresa possono diventare "fattori fissi" in una grande azienda, limitando la sua capacità di adattarsi e rispondere efficacemente alle crescenti esigenze operative. Come il capitale fisico, anche il management può dover essere ridimensionato o ristrutturato per gestire efficacemente un'organizzazione più grande.
Le diseconomie di scala dimostrano che esiste una dimensione ottimale per le aziende, oltre la quale l'aumento della produzione può effettivamente ridurre l'efficienza e aumentare i costi. Per questo motivo le aziende devono valutare costantemente le loro prestazioni operative e rimanere agili, anche quando crescono, per evitare le insidie delle diseconomie di scala.
Sintesi[modifier | modifier le wikicode]
L'obiettivo fondamentale di un'azienda è quello di massimizzare il proprio profitto, ovvero la differenza tra i ricavi totali e i costi totali. Per raggiungere questo obiettivo, un'azienda deve non solo coprire i costi espliciti, come le spese per le materie prime, i salari e gli affitti, ma anche tenere conto dei costi impliciti. Questi ultimi rappresentano i costi opportunità associati alla produzione, come i potenziali ritorni da investimenti alternativi o il salario che l'imprenditore potrebbe guadagnare altrove.
Il costo totale di un'impresa è direttamente correlato alla sua funzione di produzione, che descrive la relazione tra le quantità di input utilizzati e la quantità di output prodotto. In genere, la funzione di produzione mostra una fase di produttività marginale decrescente, il che significa che oltre un certo punto, ogni aggiunta di un fattore di produzione produce meno output aggiuntivo di quello precedente. Ciò è spesso dovuto a vincoli di capacità o a un uso meno efficiente delle risorse all'aumentare della scala di produzione.
I costi aziendali si dividono in costi fissi, che rimangono costanti indipendentemente dalla quantità prodotta, e costi variabili, che variano con la produzione. I costi fissi possono includere spese come l'affitto e i salari dei dipendenti fissi, mentre i costi variabili possono includere i costi relativi alle materie prime e alla manodopera direttamente assegnata alla produzione.
Il costo medio, che è il costo totale diviso per il numero di unità prodotte, fornisce una misura del costo per unità. Il costo marginale, invece, indica quanto costa produrre un'unità aggiuntiva. In molti casi, il costo marginale aumenta con la quantità prodotta, soprattutto dopo aver raggiunto un certo livello di produzione. Questo aumento è generalmente attribuito alla diminuzione della produttività marginale.
Il comportamento del costo medio e del costo marginale è tale che il costo medio segue una curva a forma di U. Inizialmente diminuisce all'aumentare della produzione, a causa dell'aumento della produttività marginale. Inizialmente diminuisce all'aumentare della produzione, a causa delle economie di scala e della ripartizione dei costi fissi su un numero maggiore di unità, ma poi inizia a salire quando si affermano le diseconomie di scala. La curva del costo marginale interseca la curva del costo medio nel punto in cui il costo medio è più basso, noto come punto di minima scala efficiente.
Per quanto riguarda l'orizzonte temporale, la struttura dei costi di un'azienda varia tra il breve e il lungo periodo. Molti costi considerati fissi nel breve periodo, come gli impianti e le attrezzature, possono diventare variabili nel lungo periodo, in quanto l'azienda ha la possibilità di regolare questi fattori in base alle sue decisioni di produzione. Ciò conferisce all'azienda una maggiore flessibilità per ottimizzare la struttura dei costi e quindi il potenziale di profitto a lungo termine. La capacità di un'azienda di adattare e rivedere i propri fattori produttivi nel lungo periodo è fondamentale per la sua capacità di mantenere una crescita sostenibile e di rispondere efficacemente ai cambiamenti del mercato.