Oligopole

Oligopole

Données clés

Professeur(s)	Milet, Emmanuel Sbergami, Federica Ferro-Luzzi , Giovanni
Cours	Introduction à la microéconomie

Lectures

• Introduction au cours d'introduction à la microéconomie
• Approche méthodologiques au cours d'introduction à la microéconomie
• Les forces du marché : l'offre et la demande
• Les élasticités et ses applications
• Offre, demande et politiques gouvernementales
• Surplus du consommateur et du producteur
• Les externalités et le rôle de l'État
• Les biens publics
• Les coûts de production
• Les entreprises en concurrence parfaite
• Les entreprises en monopole
• Concurrence monopolistique
• Oligopole
• Contrainte et préférences du consommateur
• Choix du consommateur
• Les problèmes d'information et les choix publics

Ce type de concurrence imparfaite caractérise les secteurs où les entreprises font face à des concurrents mais où l’intensité de la concurrence n’est pas suffisante pour qu’elles soient “preneuses de prix”. En fait, l epetit nombre d’entreprises a pour conséquence d’engager une compétition stratégique et minutieuse.

Marchés avec un faible nombre de participants.

• Duopole : deux entreprises
• Oligopole : quelques offreurs

Un marché dominé par un nombre relativement petit de vendeurs est appelé un marché concentré. Cela leur procure un pouvoir de marché car elles peuvent choisir les prix et pratiquer des prix à un coût supérieur au coût de production.

Caractéristiques: Un des points clef de l’oligopole est qu’il existe une tension entre la volonté de coopérer et la volonté d’agir en fonction de leurs propres intérêts.

• Pouvoir sur les prix, mais ce pouvoir est réduit par rapport au monopole.
• Aussi : interdépendance des décisions des offreurs (décisions stratégiques).
• La collusion est possible : souvent il est dans l’intérêt des firmes de coopérer en agissant comme si elles étaient en situation de monopole.

La théorie des jeux est l’étude du comportement des individus placés dans des situations stratégiques. Elle se prête bien à analyser le comportement d'entreprises qui se trouvent en situation d'oligopole → éléments de théorie des jeux

Languages

Español

Maximisation du profit avec et sans coopération

Hypothèses

Dans un marché spécifique où les conditions suivantes sont réunies :

• Atomicité du côté de la demande : Cela signifie qu'il y a de nombreux petits consommateurs sur le marché et qu'aucun d'entre eux n'a suffisamment d'influence individuelle pour affecter le prix ou les conditions du marché. Chaque consommateur prend le prix comme donné et agit en fonction de ses préférences individuelles.
• Bien homogène : Le bien ou le service proposé sur le marché est identique quel que soit le producteur. Il n'y a pas de différenciation entre les produits des différents offreurs. Cela signifie que les consommateurs ne préfèrent pas un produit spécifique d'un producteur particulier, mais choisissent simplement en fonction du prix.
• Pas de libre-entrée : Il existe des barrières à l'entrée sur le marché, ce qui signifie qu'un nombre fixe d'entreprises opèrent dans l'industrie. Cela peut être dû à des coûts élevés de démarrage, à des réglementations restrictives ou à d'autres facteurs qui empêchent de nouvelles entreprises d'entrer facilement sur le marché.
• Offreurs peu nombreux avec un pouvoir de marché : Bien qu'il y ait un petit nombre d'offreurs sur le marché, ils ont un certain pouvoir de marché, ce qui signifie qu'ils peuvent influencer le prix du bien ou du service. Les offreurs peuvent charger un prix supérieur au coût marginal, ce qui leur permet de réaliser des profits supplémentaires.
• Choix du volume de production : Étant donné que le bien est homogène, les entreprises en concurrence dans ce marché spécifique ne peuvent pas se différencier par le prix, la publicité ou la qualité. Par conséquent, leur principal choix stratégique est de déterminer le volume de production pour maximiser leurs profits.

Dans ce type de marché, nous pouvons nous attendre à ce que les entreprises fixent des prix supérieurs à leur coût marginal et à ce qu'il y ait une certaine interdépendance entre les offreurs. Ils peuvent chercher à coordonner leurs décisions de production afin de maintenir des niveaux de prix plus élevés et d'éviter une concurrence acharnée.

La demande d'eau potable

Dans le cas de la concurrence parfaite, il y aurait de nombreux offreurs sur le marché, ce qui signifierait qu'il n'y aurait pas d'oligopole mais plutôt une structure de marché concurrentielle. Cependant, étant donné que vous mentionnez que seuls UN et DEUX sont les deux offreurs sur le marché, nous devons supposer que l'offre d'eau potable dans ce village est un oligopole.

Dans un oligopole, les offreurs sont peu nombreux et ont un certain pouvoir de marché. Dans ce cas, UN et DEUX sont les seuls offreurs et ils exercent donc une influence sur le prix et les conditions du marché de l'eau potable.

Pour analyser la situation plus en détail, nous devons prendre en compte les hypothèses spécifiques mentionnées :

La demande d'eau potable est représentée par l'équation : $q^{D}=120-p$ ou $p=120-q$, où $q^{D}$ représente la quantité demandée et $p$ le prix. Cette équation suggère une relation inverse entre le prix et la quantité demandée. Plus le prix est élevé, moins la quantité demandée sera élevée et vice versa.

Le coût marginal est nul ($CT=CF$). Cela signifie que les coûts de production pour UN et DEUX sont constants et n'augmentent pas avec la quantité produite. Dans ce cas, les offreurs peuvent offrir l'eau potable à n'importe quel prix supérieur à zéro sans subir de coûts supplémentaires.

Maintenant, examinons les deux cas extrêmes : la concurrence parfaite et le monopole.

Concurrence parfaite : Dans une situation de concurrence parfaite, il y aurait de nombreux offreurs sur le marché. Chaque offreur serait un "price taker" et ne pourrait pas influencer le prix. Le prix serait déterminé par l'interaction de l'offre totale et de la demande totale sur le marché. Étant donné que UN et DEUX sont les seuls offreurs dans ce cas, la concurrence parfaite n'est pas applicable.

Monopole : Dans un monopole, il y aurait un seul offreur sur le marché. Le monopoleur aurait un pouvoir de marché significatif et pourrait fixer le prix en fonction de sa volonté. Cependant, étant donné que UN et DEUX sont tous deux des offreurs sur le marché de l'eau potable du village, il n'y a pas de monopole.

Il semble donc que la situation décrite dans ce village ne correspond pas aux cas extrêmes de concurrence parfaite ou de monopole. Au lieu de cela, elle correspondrait à un oligopole où UN et DEUX sont les deux seuls offreurs sur le marché de l'eau potable. Dans un oligopole, les offreurs peuvent coordonner leurs décisions de production et influencer le prix en fonction de leur pouvoir de marché.

Solution en concurrence parfaite

Dans un marché parfaitement concurrentiel, le prix serait poussé au niveau du coût marginal, qui est nul dans ce cas (Cm = 0), conformément à la loi de l'offre et de la demande.

La quantité totale consommée serait de Q = 120, ce qui correspond à la quantité maximale demandée par les consommateurs selon l'équation de demande.

Dans cet équilibre de concurrence parfaite, le prix est égal au coût marginal, ce qui signifie qu'il n'y a pas de profit économique pour les offreurs d'eau potable. Les offreurs ne réaliseraient pas de revenus positifs, mais ils pourraient encore couvrir leurs coûts de production et maintenir leur activité.

Cet équilibre est considéré comme efficient, car il permet d'allouer les ressources de manière optimale. Le prix correspond au coût marginal, ce qui garantit que la valeur marginale pour les consommateurs est égale au coût marginal de production.

Dans le cas spécifique où il n'y a que deux offreurs sur le marché de l'eau potable du village, le modèle de concurrence parfaite ne serait pas adéquat pour décrire l'équilibre du marché.

Dans le modèle de concurrence parfaite, il est supposé qu'il y a un grand nombre d'offreurs sur le marché, ce qui crée une concurrence intense et pousse les prix vers le coût marginal. Cela permettrait aux offreurs de couvrir leurs coûts et de générer des revenus.

Cependant, dans le cas où seulement deux offreurs sont présents, les conditions de la concurrence parfaite ne sont pas remplies. Les offreurs peuvent exercer un certain pouvoir de marché et influencer les prix, ce qui les empêche de se limiter au coût marginal et de ne générer aucun revenu.

Il est en effet difficile d'imaginer une activité économique viable où les offreurs ne génèrent aucun revenu. Dans ce cas, une analyse plus approfondie de la dynamique de ce marché spécifique, en tenant compte des caractéristiques de l'oligopole, serait nécessaire pour comprendre l'équilibre et les résultats économiques réels.

Solution en monopole

Dans le cas d'un monopole où UN et DEUX coopèrent, le profit serait maximisé lorsque la recette totale du marché est maximisée, étant donné qu'il n'y a pas de coût variable selon l'hypothèse donnée. Pour maximiser la recette totale, les offreurs peuvent collaborer et fixer un prix plus élevé que dans un marché concurrentiel.

Dans un monopole, UN et DEUX peuvent coordonner leurs décisions de production et fixer un prix plus élevé que dans un scénario de concurrence parfaite. Cela leur permettrait de réaliser des profits plus importants.

Le niveau de production et le prix spécifiques dépendraient des négociations entre UN et DEUX. Ils chercheraient à maximiser leur profit en trouvant un équilibre entre la demande du marché et le niveau de prix établi.

Dans le cas d'un monopole avec UN et DEUX coopérant, la maximisation du profit peut être réalisée en trouvant la quantité optimale à produire.

La fonction de profit peut être exprimée comme suit :

$\pi =RT-CT=(120-q)q-CF$

Pour maximiser le profit, nous devons déterminer la quantité optimale de production. Cela peut être fait en calculant la dérivée partielle du profit par rapport à la quantité (${\frac {\partial \pi }{\partial q}}$) et en l'égalant à zéro.

${\frac {\partial \pi }{\partial q}}=(120-2q)=0$

En résolvant cette équation, nous trouvons que la quantité optimale ($q^{*}$) est de 60. Cela signifie que les offreurs devraient produire 60 unités d'eau potable.

Le prix correspondant peut être déterminé en substituant cette valeur de $q^{*}$ dans l'équation de demande :

$p=120-q^{*}=120-60=60$

Par conséquent, le prix optimal serait de 60 unités monétaires par unité d'eau potable.

Le profit maximum ($\pi _{max}$) peut être calculé en substituant la quantité optimale ($q^{*}$) dans la fonction de profit :

$\pi _{max}=(120-q^{)}q^{-}CF=(120-60)\times 60-CF=3600-CF$

Il est important de noter que dans cette analyse, nous ne disposons pas d'informations sur les coûts fixes (CF). Par conséquent, nous ne pouvons pas déterminer la valeur exacte du profit maximum sans connaître ces informations.

Dans le cas d'un monopole où UN et DEUX coopèrent, ils pourraient en effet s'entendre pour écouler une quantité totale de 60 unités d'eau potable au prix de 60 unités monétaires par unité.

Dans ce scénario, chaque offreur vendrait la moitié de la quantité totale, soit 30 unités d'eau potable. Par conséquent, UN et DEUX réaliseraient chacun une recette de 30 unités monétaires par unité multipliée par la quantité qu'ils vendent, soit 30 x 60 = 1800 unités monétaires.

Dans le contexte économique, on parle de collusion lorsque des entreprises s'entendent pour coordonner leurs actions et fixer les quantités à produire ou les prix à appliquer sur le marché. Cette pratique anticoncurrentielle vise à limiter la concurrence et à obtenir des bénéfices supérieurs en éliminant la concurrence directe entre les entreprises. D'autre part, un cartel est une forme plus organisée de collusion. Il se produit lorsque des offreurs se regroupent formellement ou informellement pour agir ensemble et contrôler le marché. Les membres du cartel peuvent s'entendre sur les prix, les quantités, les parts de marché, les stratégies de production, etc. Le but est de maximiser les bénéfices collectifs en limitant la concurrence entre eux. Les cartels sont généralement considérés comme des pratiques anticoncurrentielles et sont souvent illégaux en raison de leurs effets négatifs sur la concurrence et le bien-être des consommateurs. Les autorités de réglementation et les organismes antitrust cherchent à détecter et à sanctionner les cartels afin de préserver un marché concurrentiel et de protéger les intérêts des consommateurs. Il est important de souligner que la coopération entre les offreurs n'est pas toujours anticoncurrentielle ou illégale. Dans certains cas, la coopération peut être bénéfique, par exemple, dans des accords de recherche et développement conjoints ou dans des partenariats pour partager les coûts d'infrastructure. Cependant, il est essentiel de respecter les lois antitrust et les réglementations pour éviter les pratiques anticoncurrentielles préjudiciables à la concurrence et aux consommateurs.

Dans de nombreux pays, les lois antitrust interdisent explicitement les accords entre les producteurs en oligopole, y compris la formation de cartels. Ces lois visent à préserver la concurrence sur le marché et à empêcher les pratiques anticoncurrentielles qui pourraient nuire aux consommateurs et à l'économie dans son ensemble. Les cartels en oligopole sont considérés comme particulièrement préjudiciables car ils permettent aux offreurs de limiter la concurrence et de fixer des prix supérieurs au niveau concurrentiel. Cela entraîne des conséquences négatives telles qu'une allocation inefficace des ressources, des prix élevés pour les consommateurs et des barrières à l'entrée pour les nouveaux entrants sur le marché. Les autorités de réglementation et les organismes antitrust surveillent de près les comportements anticoncurrentiels et cherchent à détecter et à punir les tentatives de collusion ou de formation de cartels. Les entreprises qui se livrent à de telles pratiques peuvent faire face à des sanctions financières importantes, à des poursuites judiciaires et à d'autres mesures coercitives. L'objectif des lois antitrust est de promouvoir une concurrence saine et équitable, qui encourage l'innovation, stimule l'efficacité économique et offre des choix et des prix compétitifs aux consommateurs.

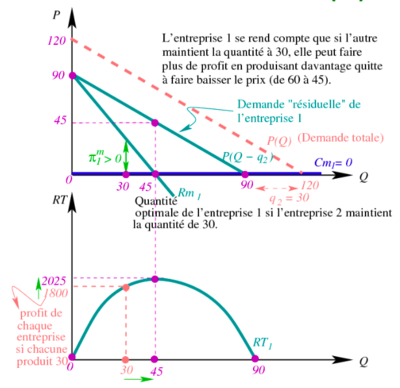
Incitation à tricher

Dans une situation dans laquelle UN, l'un des offreurs dans l'oligopole, peut chercher à accroître ses profits en augmentant sa production d'eau potable tout en comptant sur DEUX pour maintenir sa production constante. Dans cette situation, si UN décide d'augmenter sa production au-delà de 30 unités d'eau potable, cela pourrait conduire à une offre totale supérieure à la demande du marché. Cela pourrait entraîner une baisse des prix sur le marché, car l'offre excède la demande. Si UN parvient à accroître sa production tout en maintenant DEUX à une production constante de 30 unités, il pourrait bénéficier d'une part de marché plus importante et potentiellement accroître ses profits. Cependant, cela dépendra de la réaction de DEUX et de la dynamique concurrentielle entre les deux offreurs.

En soustrayant la quantité de 30 de la demande totale pour UN, cela donne une demande résiduelle pour UN de $p_{1}=90-q_{1}$.

En utilisant cette demande résiduelle, vous avez calculé la recette totale et marginale de UN, qui sont respectivement $RT_{1}=(90-q_{1})q_{1}$ et $Rm_{1}=(90-q_{1})$.

En maximisant le profit de UN, vous avez trouvé que la quantité optimale à produire pour UN serait de 45 unités ($q_{1}^{\ast }=45$) lorsque la recette marginale est égale au coût marginal ($Rm_{1}=Cm$).

Cela entraînerait une diminution du prix sur le marché, car la quantité totale sur le marché serait de 30 + 45 = 75, ce qui donnerait un prix de $p=120-75=45$. Cependant, cela permettrait à UN de générer un revenu de $45^{2}=2025$, qui est supérieur aux 1800 unités monétaires du monopole (cartel).

Équilibre sans coopération

Dans le cas où UN augmente sa production d'eau potable sans coopération, DEUX est susceptible de réagir pour préserver ses propres profits et rétablir l'équilibre sur le marché.

Si UN augmente sa production d'eau potable, cela entraînera une augmentation de l'offre totale sur le marché, ce qui pourrait faire baisser le prix. En conséquence, DEUX constatera une diminution de ses profits, car le prix de vente par unité d'eau potable sera inférieur à $45\times 30=1350$ plutôt que les 1800 du monopole (cartel)

Dans cette situation, DEUX pourrait choisir d'augmenter également sa production d'eau potable pour compenser la baisse de prix et maintenir sa part de marché. En augmentant sa production, DEUX pourrait essayer de récupérer une partie de ses profits perdus.

Dans un duopole, les offreurs UN et DEUX peuvent réagir et contre-réagir en ajustant leur production en réponse aux actions de l'autre offreur. Ce processus de réaction et contre-réaction se poursuit jusqu'à ce qu'un équilibre du duopole soit atteint.

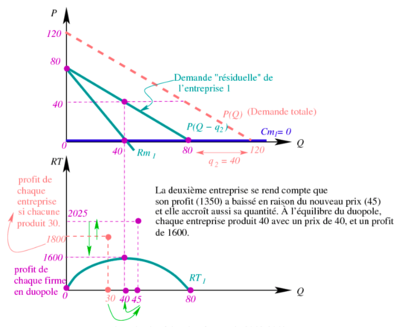
Dans ce cas spécifique, pour déterminer l'équilibre du duopole, nous pouvons égaliser les recettes marginales des offreurs à zéro, puisque le coût marginal est nul (Cm = 0). Cela peut être exprimé comme suit :

$Rm_{1}=120-q_{2}-2q_{1}=Rm_{2}=120-q_{1}-2q_{2}=0$

En résolvant ces équations simultanées, nous trouvons que la quantité optimale de production pour UN et DEUX serait de 40 unités chacun ($q_{1}^{}=q_{2}^{}=40$). Le prix correspondant serait également de 40 unités monétaires par unité d'eau potable.

À cet équilibre, les offreurs UN et DEUX réaliseraient chacun une recette totale de 40 unités monétaires par unité multipliée par la quantité produite, soit une recette totale de 1600 unités monétaires pour chaque offreur.

Dans un équilibre de duopole, aucun des deux offreurs ne souhaite modifier sa quantité de production, car les profits marginaux sont nuls pour les deux. Dans le cas spécifique où UN et DEUX produisent chacun 40 unités d'eau potable dans le duopole, cela signifie que les offreurs ont atteint un point d'équilibre où leurs profits marginaux sont nuls. Cela signifie que tout ajustement de la quantité de production par l'un des offreurs ne conduirait pas à une augmentation de ses profits. L'équilibre de duopole est atteint lorsque les offreurs ont ajusté leur production de manière à ce que leurs recettes marginales soient égales à leurs coûts marginaux, qui dans ce cas sont nuls (Cm = 0). À cet équilibre, les offreurs ne sont pas incités à modifier leur quantité de production, car cela n'apporterait aucun avantage supplémentaire en termes de profit.

Dans le cas de l'équilibre du duopole, où UN et DEUX produisent chacun 40 unités d'eau potable, le profit de chaque entreprise est de 1600 unités monétaires. Cela est inférieur au profit de 1800 unités monétaires que chaque entreprise aurait réalisé dans le cas de la solution de monopole. Dans le cas du monopole, où UN et DEUX coopèrent pour fixer la quantité totale à 60 unités, chaque entreprise bénéficie d'un pouvoir de marché et peut facturer un prix plus élevé, ce qui conduit à des profits plus élevés. En revanche, dans le duopole, chaque entreprise doit prendre en compte les réactions de l'autre entreprise et ne peut pas exercer un pouvoir de marché aussi fort. Cela conduit à une concurrence plus intense et à une pression sur les prix, ce qui réduit les profits des deux entreprises par rapport à la solution de monopole. Cela met en évidence le fait que, dans un oligopole ou un duopole, la concurrence entre les offreurs peut réduire les profits par rapport à une situation de monopole, où un seul offreur a un pouvoir de marché plus fort.

Maximisation du profit en duopole : cas général

Dans un duopole, la maximisation du profit pour chaque offreur peut être analysée en prenant en compte la réaction de l'autre offreur. Pour cela, nous devons tenir compte des fonctions de demande et de coût de chaque entreprise.

Supposons que UN et DEUX soient les deux offreurs dans le duopole, et que leurs fonctions de demande respectives soient représentées par $q_{1}^{D}$ et $q_{2}^{D}$. Le prix sur le marché serait déterminé par l'équilibre des quantités offertes par UN et DEUX.

La maximisation du profit pour UN peut être exprimée comme suit :

$\max _{q_{1}}\pi _{1}=(p-Cm_{1})\cdot q_{1}$

Sous contrainte de la demande totale :

$q^{D}=q_{1}+q_{2}$

De manière similaire, la maximisation du profit pour DEUX peut être exprimée comme suit :

$\max _{q_{2}}\pi _{2}=(p-Cm_{2})\cdot q_{2}$

Sous la même contrainte de la demande totale :

$q^{D}=q_{1}+q_{2}$

Pour trouver l'équilibre du duopole, nous devons résoudre ce système d'équations simultanées. Cela dépendra des fonctions de demande spécifiques, des coûts marginaux de chaque entreprise, ainsi que des contraintes et des paramètres du marché.

Maximisation du profit de l'entreprise 1 :

$\max _{q_{1}}\pi _{1}=p(Q)q_{1}-CT(q_{1})$

Sous contrainte de la demande totale :

$Q=q_{1}+q_{2}$

Condition de première ordre (Rm = Cm) pour l'entreprise 1 :

$Rm_{1}=p+{\frac {\partial p}{\partial Q}}q_{1}={\frac {\partial CT}{\partial q_{1}}}Cm_{1}$

Maximisation du profit de l'entreprise 2 :

$\max _{q_{2}}\pi _{2}=p(Q)q_{2}-CT(q_{2})$

Sous contrainte de la demande totale :

$Q=q_{1}+q_{2}$

Condition de première ordre (Rm = Cm) pour l'entreprise 2 :

$Rm_{2}=p+{\frac {\partial p}{\partial Q}}q_{2}={\frac {\partial CT}{\partial q_{2}}}Cm_{2}$

Ces équations représentent les conditions nécessaires pour maximiser le profit de chaque entreprise dans un duopole. L'objectif est de trouver les niveaux optimaux de production pour chaque entreprise qui maximisent leurs profits respectifs, tout en respectant la contrainte de la demande totale sur le marché.

Dans les conditions de première ordre pour chaque entreprise, les termes $p$ et ${\frac {\partial p}{\partial Q}}$ dépendent à la fois de $q_{1}$ et de $q_{2}$. Cela signifie que chaque entreprise prend en compte les décisions de l'autre entreprise lorsqu'elle prend ses propres décisions de production. Dans un duopole, les offreurs sont interdépendants et les choix de production de chaque entreprise ont un impact sur les conditions du marché, y compris le prix. Par conséquent, chaque entreprise tient compte des réactions possibles de l'autre entreprise lorsqu'elle détermine sa propre quantité de production. Lorsque l'entreprise 1 prend sa décision de production, elle anticipe l'effet que cela aura sur le prix et la demande totale, qui sont des facteurs déterminés à la fois par sa propre production et par celle de l'entreprise 2. De même, lorsque l'entreprise 2 prend sa décision de production, elle tient compte de l'impact sur le prix et la demande totale, qui dépendent à la fois de sa propre production et de celle de l'entreprise 1. Cette interdépendance des décisions de production crée une dynamique concurrentielle entre les offreurs dans un duopole. Chaque entreprise cherche à maximiser son propre profit en tenant compte de la réaction de l'autre entreprise. Cela peut conduire à des ajustements stratégiques et à des contre-réactions entre les offreurs. L'interaction des choix des deux entreprises est essentielle pour comprendre la dynamique concurrentielle dans un duopole. Les modèles d'équilibre du duopole prennent en compte cette interdépendance des décisions et cherchent à déterminer les niveaux optimaux de production pour chaque entreprise qui maximisent leurs profits respectifs, compte tenu des réactions mutuelles.

Équilibre de l'oligopole

Lorsque les firmes en oligopole choisissent individuellement leur production pour maximiser leur profit :

• La quantité totale produite dans l'oligopole est généralement supérieure à celle dans un monopole, mais inférieure à celle dans une situation de concurrence parfaite. Cela est dû au fait que chaque entreprise en oligopole a une certaine marge de pouvoir de marché et peut augmenter sa production par rapport à un monopole, mais il y a toujours une certaine concurrence qui limite la quantité totale produite.
• Le prix fixé par l'oligopole est généralement inférieur au prix d'un monopole, mais supérieur au prix concurrentiel qui équivaut au coût marginal (Cm). Les entreprises en oligopole ont une certaine marge de pouvoir de marché et peuvent fixer un prix légèrement supérieur au coût marginal pour maximiser leurs profits.
• Les profits réalisés par les entreprises en oligopole sont généralement inférieurs à ceux d'un monopole, car la concurrence entre les entreprises limite leur capacité à exercer un pouvoir de marché total. Cependant, les profits dans un oligopole sont généralement supérieurs à ceux de la concurrence parfaite, où la pression concurrentielle est plus forte et les prix sont égaux au coût marginal.

Ces résultats soulignent les caractéristiques spécifiques de l'oligopole, où les entreprises ont une certaine capacité de contrôle sur les prix et les quantités, mais sont toujours confrontées à la concurrence entre elles. Les entreprises en oligopole cherchent à maximiser leurs profits tout en tenant compte des réactions de leurs concurrents, ce qui peut conduire à des niveaux de production et des prix différents de ceux observés dans un monopole ou une situation de concurrence parfaite.

A l'équilibre de l'oligopole, le prix (p) est généralement supérieur au coût marginal (Cm), ce qui crée un mark-up ou un pouvoir de marché. Le mark-up représente la différence entre le prix fixé par les entreprises en oligopole et leur coût marginal. En d'autres termes, c'est l'écart entre le prix de vente et le coût réel d'une unité de production. Lorsque le mark-up est positif, cela indique que les entreprises en oligopole ont un certain pouvoir de marché et peuvent facturer un prix supérieur à leur coût marginal. Cela leur permet de réaliser des profits supplémentaires par rapport à la situation de concurrence parfaite où le prix est égal au coût marginal. Le pouvoir de marché dans un oligopole découle de plusieurs facteurs, notamment la concentration du marché, les barrières à l'entrée, la différenciation des produits et les interactions stratégiques entre les offreurs. Ces facteurs permettent aux entreprises en oligopole de limiter la concurrence et d'exercer une certaine influence sur le prix.

L'effet de la taille

L'augmentation du nombre de vendeurs sur un marché oligopolistique peut avoir un impact sur le prix et les quantités vendues. Voici les deux effets principaux à prendre en compte :

• L'effet quantité : L'augmentation du nombre de vendeurs entraîne une augmentation de la quantité totale offerte sur le marché. Cela peut avoir un effet à la fois positif et négatif sur les profits des vendeurs. D'une part, vendre une unité supplémentaire au prix courant permet d'augmenter les profits. Cela est dû au fait que le prix de vente est supérieur au coût marginal pour chaque unité vendue. Par conséquent, l'augmentation de la quantité vendue peut contribuer à augmenter les profits totaux des vendeurs. D'autre part, une augmentation de la production totale peut entraîner une diminution du prix sur le marché. Cela peut réduire le profit par unité pour chaque unité vendue, car le prix est plus bas. Ainsi, bien que l'augmentation de la quantité vendue puisse augmenter les profits totaux, elle peut également entraîner une diminution du profit par unité.
• L'effet prix : L'augmentation de la production totale due à l'entrée de nouveaux vendeurs peut exercer une pression à la baisse sur le prix du marché. Une plus grande offre peut conduire à une concurrence accrue entre les vendeurs et à une diminution du pouvoir de marché. Par conséquent, le prix peut diminuer en raison de la pression concurrentielle exercée par les nouveaux vendeurs. Cette baisse du prix peut réduire le profit par unité pour chaque vendeur, car le prix de vente est plus bas. Ainsi, l'effet prix peut contrebalancer l'effet quantité positif sur les profits.

En résumé, l'augmentation du nombre de vendeurs dans un marché oligopolistique peut avoir un impact complexe sur le prix et les quantités vendues. L'effet quantité peut augmenter les profits totaux, mais l'effet prix peut diminuer le profit par unité. Les résultats dépendront des caractéristiques spécifiques du marché, de la concurrence entre les vendeurs et de la réaction des consommateurs aux changements de prix.

au fur et à mesure que le nombre de vendeurs en situation d'oligopole augmente, le marché tend à se rapprocher d'un marché concurrentiel. Cela peut entraîner des ajustements dans le prix et les quantités produites, se rapprochant des niveaux observés dans un marché concurrentiel idéal. Voici les principaux mécanismes en jeu :

• Le prix converge vers le coût marginal : Dans un marché oligopolistique, les entreprises ont un certain pouvoir de marché et peuvent fixer des prix supérieurs à leurs coûts marginaux. Cependant, avec l'entrée de nouveaux vendeurs, la concurrence s'intensifie et le pouvoir de marché diminue. Les vendeurs ont moins de marge pour fixer des prix élevés et sont davantage incités à s'aligner sur le coût marginal pour rester compétitifs. Par conséquent, le prix tend à converger vers le coût marginal à mesure que le nombre de vendeurs augmente.
• La quantité produite se rapproche du niveau socialement efficace : Dans un marché concurrentiel idéal, la quantité produite serait telle que le coût marginal égalise la demande marginale, ce qui correspondrait à un niveau socialement efficace. Dans un oligopole, la quantité produite est généralement inférieure à ce niveau en raison du pouvoir de marché des vendeurs. Cependant, avec l'entrée de nouveaux vendeurs, la concurrence s'intensifie, ce qui conduit à une augmentation de la quantité produite. À mesure que le nombre de vendeurs augmente, la quantité totale produite se rapproche du niveau socialement efficace, car la concurrence entre les vendeurs stimule une augmentation de la production.

Cette convergence vers un marché concurrentiel dépendra de plusieurs facteurs, tels que la facilité d'entrée sur le marché, les barrières à l'entrée, la différenciation des produits et les stratégies des vendeurs. De plus, la dynamique concurrentielle peut prendre du temps pour se développer et atteindre cet équilibre concurrentiel. En résumé, à mesure que le nombre de vendeurs en situation d'oligopole augmente, le marché tend à se rapprocher d'un marché concurrentiel, avec une convergence du prix vers le coût marginal et une augmentation de la quantité produite se rapprochant du niveau socialement efficace. Cependant, la réalisation de cette convergence dépend des caractéristiques spécifiques du marché et des comportements des vendeurs.

La théorie des jeux et l'économie de la coopération

La théorie des jeux est un domaine de l'économie qui étudie les décisions prises par des agents économiques (joueurs) lorsqu'ils sont confrontés à des situations d'interaction stratégique. Elle s'intéresse notamment à la manière dont les choix des joueurs sont influencés par les choix des autres joueurs, et comment ces interactions stratégiques peuvent conduire à des résultats différents de ceux qui seraient obtenus dans des situations où les joueurs agiraient de manière isolée.

L'économie de la coopération est une branche de l'économie qui se concentre sur l'analyse des situations où les agents économiques ont la possibilité de coopérer pour atteindre des résultats mutuellement bénéfiques. Elle examine les incitations à la coopération, les mécanismes de coordination et les obstacles potentiels à la coopération.

La théorie des jeux est un outil puissant pour analyser les situations de coopération en économie. Elle permet de modéliser les interactions stratégiques entre les agents, d'identifier les stratégies optimales et de comprendre les résultats qui peuvent émerger des différentes configurations de jeu.

Dans le contexte de la coopération en économie, la théorie des jeux peut être utilisée pour étudier des situations telles que la formation de cartels, les accords de partage de bénéfices, les coalitions d'entreprises, les négociations contractuelles, etc. Elle permet d'analyser les incitations des acteurs à coopérer, les problèmes de confiance, les stratégies de répétition et de punition, ainsi que les mécanismes de résolution des conflits.

L'économie de la coopération cherche à comprendre comment les individus peuvent surmonter les incitations à agir de manière égoïste et à coopérer de manière bénéfique pour tous. Elle explore les conditions nécessaires à la coopération durable, les mécanismes de coordination et les politiques publiques qui peuvent favoriser la coopération.

En combinant la théorie des jeux et l'économie de la coopération, les économistes peuvent analyser les incitations à la coopération, les stratégies de négociation, les structures de gouvernance et les arrangements institutionnels qui peuvent encourager la coopération et améliorer les résultats économiques. Cela permet de mieux comprendre les dynamiques de coopération dans différents domaines, tels que les relations entre les entreprises, les négociations internationales, les interactions entre consommateurs et producteurs, etc.

Eléments de théorie des jeux

La théorie des jeux est l'étude du comportement des individus (ou des joueurs) placés dans des situations stratégiques où les choix d'un joueur dépendent des choix des autres joueurs. Elle examine comment les décisions individuelles interagissent pour déterminer les résultats collectifs.

Dans la théorie des jeux, une situation stratégique est caractérisée par un ensemble de joueurs, un ensemble d'actions possibles pour chaque joueur, et des paiements ou des résultats associés à chaque combinaison d'actions. Les joueurs cherchent à maximiser leurs gains ou leurs profits en choisissant la meilleure action en fonction de leurs propres préférences et des choix des autres joueurs. La théorie des jeux propose différents modèles mathématiques et concepts pour analyser ces situations stratégiques. Elle étudie des notions telles que les jeux à somme nulle (où les gains d'un joueur sont égaux aux pertes des autres joueurs), les jeux coopératifs (où les joueurs peuvent former des coalitions et négocier des accords), les jeux répétés (où les joueurs interagissent plusieurs fois) et bien d'autres.

La théorie des jeux permet de déterminer les équilibres de Nash, qui sont des combinaisons d'actions où aucun joueur n'a intérêt à dévier unilatéralement de sa stratégie compte tenu des choix des autres joueurs. Elle permet également d'étudier les stratégies dominantes (stratégies qui sont optimales quelles que soient les actions des autres joueurs), les stratégies mixtes (combinaisons probabilistes d'actions), et bien d'autres concepts. La théorie des jeux trouve des applications dans de nombreux domaines, tels que l'économie, la science politique, la biologie, la psychologie, etc. Elle est utilisée pour analyser des situations de négociation, des marchés concurrentiels, des conflits armés, des interactions sociales, des processus de prise de décision collective, et bien d'autres scénarios où les interactions stratégiques jouent un rôle clé.

Une stratégie dans la théorie des jeux représente un choix parmi différentes décisions possibles qu'un individu peut prendre, en tenant compte des réactions potentielles des autres individus par rapport à sa propre décision. Une stratégie détermine le comportement prévu d'un joueur dans une situation donnée. Un jeu, quant à lui, est la combinaison d'un ensemble de stratégies pour chaque joueur, ce qui conduit à des gains ou des pertes différents en fonction des réactions des autres joueurs. Dans un jeu, tous les joueurs sont supposés agir de manière rationnelle, c'est-à-dire qu'ils cherchent à maximiser leurs gains ou minimiser leurs pertes en choisissant la meilleure stratégie en fonction de leurs préférences et des choix des autres joueurs.

Un jeu peut être statique ou dynamique. Dans un jeu statique, les joueurs prennent leurs décisions simultanément, sans avoir d'information sur les choix des autres joueurs au moment de prendre leur décision. Dans un jeu dynamique, les joueurs prennent leurs décisions de manière séquentielle, en tenant compte des actions prises précédemment par les autres joueurs. Les jeux dynamiques peuvent être répétés, ce qui signifie que les joueurs interagissent plusieurs fois avec les mêmes adversaires, ou séquentiels, où les joueurs prennent des décisions dans un ordre déterminé. La théorie des jeux permet d'analyser les différentes combinaisons de stratégies possibles dans un jeu, de déterminer les équilibres de Nash (les combinaisons de stratégies où aucun joueur n'a intérêt à dévier unilatéralement), et d'étudier les dynamiques d'interaction et les résultats collectifs dans une variété de contextes.

L'incertitude peut être intégrée dans la théorie des jeux lorsqu'un joueur adopte une stratégie avec une probabilité donnée. Cela permet de modéliser les situations où les joueurs ne sont pas certains des choix des autres joueurs et prennent des décisions en tenant compte de cette incertitude. L'incorporation de l'incertitude dans les jeux peut se faire à travers l'utilisation de stratégies mixtes, qui sont des combinaisons probabilistes de différentes actions. Plutôt que de choisir une seule action de manière déterministe, un joueur peut décider de jouer différentes actions avec des probabilités spécifiques. Les stratégies mixtes permettent de modéliser le comportement des joueurs dans des situations où il y a une certaine incertitude quant aux choix des autres joueurs.

Dans une perspective dynamique, le choix de stratégies crédibles revêt une grande importance. Les stratégies crédibles sont des stratégies que les joueurs sont incités à suivre et qui sont soutenues par des incitations appropriées. Dans un jeu séquentiel ou répété, les joueurs doivent prendre en compte la façon dont leurs actions passées ou futures peuvent influencer les actions des autres joueurs et vice versa. Le choix de stratégies crédibles est crucial pour maintenir la cohérence des actions dans le temps et pour obtenir des résultats optimaux. Le concept de stratégies crédibles est souvent lié à la notion d'équilibre parfait en sous-jeux, qui est un concept utilisé dans les jeux séquentiels pour décrire les séquences d'actions cohérentes que les joueurs sont incités à suivre. Les équilibres parfaits en sous-jeux fournissent des prédictions sur les choix stratégiques que les joueurs sont susceptibles de faire dans des jeux où les décisions sont prises de manière séquentielle.

Théorie des jeux et oligopole

Dans un marché oligopolistique, chaque entreprise est consciente de l'impact des actions des autres entreprises sur son propre profit. La théorie des jeux offre un cadre d'analyse approprié pour étudier les interactions stratégiques entre ces entreprises.

Chaque entreprise dans un marché oligopolistique peut être considérée comme un joueur dans un jeu, où chaque joueur cherche à maximiser son propre profit. Les décisions prises par chaque entreprise, telles que la quantité produite, le prix fixé ou les stratégies de marketing, ont un impact direct sur son profit, mais également sur les profits des autres entreprises présentes sur le marché. En raison de l'interdépendance des décisions, chaque entreprise doit prendre en compte les actions et les réactions potentielles des autres entreprises. Elles doivent anticiper comment les autres entreprises réagiront à leurs propres choix et adapter leur stratégie en conséquence. Par exemple, si une entreprise décide d'augmenter sa production, elle doit tenir compte de la façon dont les autres entreprises réagiront et comment cela affectera le prix et la demande sur le marché.

La théorie des jeux fournit des outils pour modéliser ces interactions stratégiques et analyser les résultats possibles. Elle permet de définir des stratégies pour chaque entreprise, de déterminer les équilibres de Nash (les combinaisons de stratégies où aucun joueur n'a intérêt à dévier unilatéralement), et d'étudier les résultats collectifs qui émergent de ces interactions. Dans le contexte de l'oligopole, la théorie des jeux peut être utilisée pour analyser différentes situations stratégiques, telles que la fixation des prix, la collusion, la concurrence à la Cournot ou à la Bertrand, la publicité concurrentielle, et bien d'autres. Elle permet d'explorer les incitations à coopérer ou à se comporter de manière non coopérative, et d'analyser les conséquences sur le profit des entreprises et le bien-être des consommateurs.

La particularité absente de la concurrence parfaite, du monopole et en partie de la concurrence monopolistique dans le contexte de l'oligopole est l'interdépendance stratégique entre les entreprises. Dans ces autres structures de marché, les entreprises peuvent généralement prendre leurs décisions indépendamment des actions des autres entreprises et de leur impact sur le marché. En revanche, dans un marché oligopolistique, les décisions prises par une entreprise ont un impact direct sur les autres entreprises et vice versa. Les entreprises sont conscientes que leurs actions peuvent influencer le comportement et les performances des autres entreprises, et elles doivent en tenir compte lorsqu'elles prennent leurs propres décisions stratégiques.

L'interdépendance stratégique dans un oligopole peut se manifester de différentes manières. Par exemple, une entreprise peut prendre en compte les réactions potentielles des autres entreprises lorsqu'elle décide de fixer son prix, de modifier sa production ou de lancer de nouvelles stratégies de marketing. Elle peut anticiper comment les autres entreprises réagiront et ajuster ses propres choix en conséquence. Cette interdépendance stratégique rend l'analyse de l'oligopole plus complexe que celle des autres structures de marché. La théorie des jeux, en tant qu'outil analytique, est particulièrement utile pour modéliser et étudier ces interactions stratégiques dans un oligopole. Elle permet de comprendre comment les décisions prises par chaque entreprise sont influencées par les actions des autres entreprises et comment cela affecte les résultats sur le marché.

Dans de nombreux jeux oligopolistiques, les actions sont prises de manière simultanée, ce qui signifie que chaque joueur prend sa décision sans connaître les choix des autres joueurs au moment de prendre sa décision. Cela crée une situation d'information imparfaite, car chaque joueur ne dispose pas de toutes les informations sur les décisions prises par les autres joueurs. Dans ce contexte, chaque joueur doit prendre des décisions stratégiques en se basant sur son propre jugement et ses attentes quant aux actions des autres joueurs. Ils peuvent formuler des hypothèses sur les choix possibles des autres joueurs, mais ils ne peuvent pas connaître avec certitude les décisions réelles prises par leurs adversaires.

L'information imparfaite ajoute une dimension d'incertitude et de stratégie à la dynamique du jeu. Les joueurs doivent essayer d'anticiper les actions des autres joueurs en fonction de leurs propres objectifs, des caractéristiques du marché et de leur perception de la situation. Ils peuvent utiliser des modèles, des indices ou des signaux pour formuler leurs attentes et prendre leurs décisions. La prise de décision en situation d'information imparfaite dans un jeu oligopolistique peut être très complexe, car chaque joueur doit évaluer les différentes actions possibles et les réponses potentielles des autres joueurs. La théorie des jeux offre des outils pour analyser et modéliser cette situation, en utilisant des concepts tels que les équilibres de Nash, les stratégies mixtes et les stratégies dominantes.

L'équilibre de Nash

John F. Nash a apporté des contributions importantes à la théorie des jeux non coopératifs, ce qui lui a valu le prix Nobel d'économie en 1994. Son travail a permis de développer une notion fondamentale appelée "l'équilibre de Nash". L'équilibre de Nash, nommé d'après John Nash, est une situation dans laquelle aucun joueur n'a intérêt à dévier unilatéralement de sa stratégie, compte tenu des choix des autres joueurs. Autrement dit, chaque joueur atteint une situation où, étant donné les actions des autres joueurs, il n'a pas intérêt à changer sa propre action.

L'équilibre de Nash est un concept clé dans la théorie des jeux non coopératifs car il permet de prédire comment les joueurs vont se comporter dans une situation de jeu. Il représente un point d'équilibre stable où les joueurs sont incités à maintenir leur stratégie actuelle car tout changement unilatéral ne leur apporterait pas de gains supplémentaires. L'équilibre de Nash peut être atteint dans différents types de jeux, tels que les jeux à somme nulle, les jeux coopératifs, les jeux séquentiels ou les jeux simultanés. Il peut exister plusieurs équilibres de Nash dans un jeu, et certains équilibres peuvent être plus prévisibles ou plus favorables que d'autres en termes de résultats collectifs.

Les travaux de John Nash ont considérablement enrichi la théorie des jeux non coopératifs et ont permis de mieux comprendre les interactions stratégiques entre les joueurs. Son apport a ouvert la voie à de nombreuses extensions et applications de la théorie des jeux dans divers domaines, tels que l'économie, la politique, la biologie et les sciences sociales.

Le principe fondamental de l'équilibre non coopératif de Nash est que chaque joueur choisit sa meilleure stratégie en tenant compte des stratégies des autres joueurs comme données. Dans cette situation, aucun joueur n'a intérêt à dévier unilatéralement de sa stratégie, car cela ne lui apporterait pas de gains supplémentaires. En d'autres termes, l'équilibre de Nash est un point d'équilibre où chaque joueur prend la meilleure décision possible, en anticipant les choix des autres joueurs, et où aucun joueur n'a d'incitation à modifier sa propre stratégie. Si tous les joueurs sont au point d'équilibre de Nash, il n'y a pas de déviations unilatérales rentables.

Ce concept d'équilibre de Nash est basé sur le principe de rationalité des joueurs. Chaque joueur suppose que les autres joueurs sont également rationnels et choisissent leurs stratégies de manière optimale, compte tenu des informations disponibles. Par conséquent, lorsqu'ils prennent leurs décisions, les joueurs tiennent compte des réactions potentielles des autres joueurs et choisissent leur stratégie en conséquence. Il est important de noter que l'équilibre de Nash peut ne pas être unique dans certains jeux. Il peut y avoir plusieurs équilibres de Nash possibles, et certains peuvent être plus prévisibles ou plus favorables que d'autres. Dans ces cas, il est nécessaire de considérer des critères supplémentaires pour déterminer lequel des équilibres de Nash est le plus approprié, tels que la stabilité, l'efficacité économique ou les normes sociales.

En résumé, l'équilibre non coopératif de Nash est atteint lorsque chaque joueur choisit sa meilleure stratégie en considérant les stratégies des autres comme données, et aucun joueur n'a d'incitation à dévier unilatéralement. Cela repose sur le principe de rationalité des joueurs et est basé sur l'idée que les joueurs anticipent les réactions des autres joueurs.

Il est important de noter que l'équilibre non coopératif de Nash ne garantit pas nécessairement un résultat optimal pour tous les participants. Dans certains cas, l'équilibre de Nash peut conduire à des résultats sous-optimaux, où les gains des joueurs sont inférieurs à ce qu'ils pourraient obtenir dans d'autres situations. L'équilibre de Nash se produit lorsque chaque joueur choisit la meilleure stratégie en tenant compte des stratégies des autres joueurs comme données. Cependant, cela ne signifie pas que cette combinaison de stratégies aboutit à une situation globalement optimale. Dans certains jeux, il peut exister des situations où une coopération entre les joueurs pourrait conduire à des résultats meilleurs pour tous les participants. Cependant, en l'absence de mécanismes de coopération ou d'incitations appropriées, les joueurs peuvent ne pas parvenir à un équilibre coopératif et rester dans un équilibre non coopératif de Nash. Les situations d'équilibre non coopératif de Nash peuvent être caractérisées par des incitations à l'action individuelle, où les joueurs cherchent à maximiser leurs propres gains sans tenir compte des gains collectifs ou de l'efficacité globale. Cela peut conduire à des résultats sous-optimaux où les joueurs ne parviennent pas à coopérer efficacement et où les gains collectifs sont inférieurs à leur potentiel maximal. Dans certains cas, des mécanismes externes tels que la régulation, les incitations économiques ou les institutions peuvent être nécessaires pour encourager la coopération et atteindre des résultats plus optimaux. La théorie des jeux coopératifs, par exemple, étudie les situations où les joueurs peuvent s'engager dans des coalitions et négocier des solutions coopératives qui peuvent conduire à des résultats plus avantageux pour tous.

Lorsque chaque joueur dispose d'une stratégie dominante, l'équilibre de Nash dans un jeu est facilement déterminé. Une stratégie dominante est une stratégie qui est la meilleure pour un joueur, quelle que soit la stratégie jouée par les autres joueurs. Lorsqu'il y a des stratégies dominantes pour tous les joueurs dans un jeu, chaque joueur choisit sa stratégie dominante, car c'est celle qui maximise son propre gain, indépendamment des choix des autres joueurs. Dans cette situation, l'équilibre de Nash est atteint simplement en observant les stratégies dominantes de chaque joueur. Par exemple, dans le célèbre jeu du dilemme du prisonnier, où deux suspects sont interrogés séparément et doivent décider s'ils coopèrent (gardent le silence) ou trahissent (collaborent avec les autorités), il existe une stratégie dominante pour chaque joueur : trahir. Peu importe ce que l'autre joueur choisit, la trahison est la meilleure stratégie pour chaque joueur, car elle minimise la peine maximale encourue. Dans de tels cas, l'équilibre de Nash est atteint simplement en jouant les stratégies dominantes. Aucun joueur n'a d'incitation à dévier de sa stratégie dominante, car cela ne lui apporterait pas de gains supplémentaires.

Le dilemme du prisonnier

Le dilemme du prisonnier est un exemple classique qui met en évidence la difficulté de maintenir la coopération entre les individus, même lorsque la coopération serait mutuellement avantageuse.

Dans le dilemme du prisonnier, deux suspects sont interrogés séparément et doivent décider s'ils coopèrent (gardent le silence) ou trahissent (collaborent avec les autorités). Le tableau de gains montre que la meilleure issue pour les deux suspects serait de coopérer en gardant le silence, car cela conduirait à une peine moindre pour chacun. Cependant, étant donné l'incertitude quant à la décision de l'autre joueur, il y a une incitation à trahir afin d'obtenir une peine encore plus réduite si l'autre suspect choisit de coopérer. Ce dilemme illustre la difficulté de maintenir la coopération lorsque les individus sont confrontés à des incitations à court terme ou à l'incertitude quant aux choix des autres. Même si la coopération serait mutuellement avantageuse, il peut y avoir une tentation de trahir pour obtenir des gains personnels plus élevés, en supposant que l'autre partie choisira également de trahir.

Cela est également applicable dans de nombreux contextes économiques, y compris les situations d'oligopole. Les entreprises peuvent être confrontées à des incitations à agir de manière non coopérative, même si une coopération mutuellement avantageuse pourrait conduire à de meilleurs résultats pour toutes les parties. Les entreprises peuvent craindre que les autres ne respectent pas les accords, ou elles peuvent chercher à obtenir un avantage concurrentiel en trahissant les ententes de coopération. Cette problématique de maintenir la coopération dans des situations stratégiques est un défi majeur dans de nombreux domaines, et elle a été largement étudiée dans le cadre de la théorie des jeux. Les chercheurs ont exploré différentes stratégies et mécanismes pour encourager la coopération, tels que les incitations économiques, les sanctions, les normes sociales ou les mécanismes de réputation.

Dans le contexte du dilemme du prisonnier classique, les deux suspects sont arrêtés et mis dans des cellules séparées, ce qui rend la communication et la coopération directe entre eux impossible. Dans cette situation, chaque suspect est confronté à un choix individuel : coopérer (garder le silence) ou trahir (collaborer avec les autorités). Le paradoxe du dilemme du prisonnier réside dans le fait que même si la meilleure solution pour les deux suspects serait de coopérer en gardant le silence, il existe une incitation individuelle à trahir pour obtenir une peine réduite si l'autre suspect trahit également.

Dans de nombreux systèmes juridiques, un aveu d'un des suspects peut être considéré comme une preuve suffisante pour la condamnation, même si l'autre suspect persiste à nier. Cela reflète le fait que la coopération entre les suspects est difficile à maintenir en raison de l'incertitude quant à la décision de l'autre et des incitations individuelles à trahir pour réduire sa propre peine.

La dynamique du dilemme du prisonnier met en évidence le défi de la coopération en l'absence de communication et de confiance mutuelle. Chaque suspect est incité à prendre la décision qui maximise ses propres gains, même si cela peut conduire à un résultat global sous-optimal.

Equilibre de Nash unique: (Avoue, Avoue). Equilibre non-optimal: les deux joueurs pourraient améliorer leur situation en se taisant. La coopération est difficile à maintenir car elle n’est pas un choix rationnel au niveau individuel. NB: ici, le jeu est symétrique, mais ce n’est pas nécessairement le cas.

Dans le dilemme du prisonnier, il est crucial de prendre en compte les différents résultats possibles en fonction des choix de coopération ou de trahison des deux prisonniers. Dans ce cas précis, les peines associées aux différentes combinaisons de choix sont les suivantes :

• Si aucun des prisonniers n'avoue, ils écopent tous deux d'une peine mineure de 1 an de prison.
• Si les deux prisonniers avouent, ils subissent tous deux la peine prévue pour le délit, soit une peine plus sévère de 8 ans de prison.
• Si un prisonnier avoue et l'autre ne le fait pas, celui qui avoue bénéficie d'une mesure de clémence et est immédiatement libéré, tandis que l'autre subit une peine plus grave de 20 ans de prison pour obstruction à la justice.

Ces informations fournissent un cadre plus complet pour analyser les incitations et les choix des prisonniers. Chaque prisonnier doit évaluer les résultats potentiels en fonction de ses propres choix et de ceux de l'autre prisonnier.

Dans cette situation, les prisonniers sont confrontés à un dilemme difficile. Si chacun choisit de coopérer et de garder le silence, ils bénéficieraient tous deux de la peine mineure d'un an de prison. Cependant, chaque prisonnier a l'incitation individuelle à trahir, car cela peut lui permettre d'éviter une peine plus sévère ou même d'être immédiatement libéré en cas d'aveu de l'autre prisonnier.

Cette configuration met en évidence le conflit entre l'intérêt individuel et l'intérêt collectif. Bien que la coopération en gardant le silence soit mutuellement avantageuse, il y a une incitation individuelle à trahir pour éviter une peine plus sévère. Cette dynamique met en évidence les difficultés de maintenir la coopération dans des situations de jeu stratégique.

Un jeu de course à l'armement

Stratégie dominante dans le jeu du dilemme du prisonnier: "avoue" ici: "s'armer".

Le duopole comme dilemme du prisonnier

Tout comme la logique de l’intérêt individuel conduit les prisonniers à avouer, ce même intérêt individuel engendre des difficultés pour l’oligopole à maintenir une situation coopérative (qui serait la solution optimale pour les deux), caractérisée par une production faible, des prix élevés et des profits de monopole.

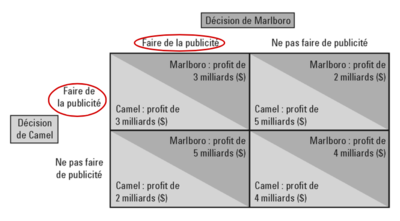
Un jeu de publicité

Un jeu de ressources communes

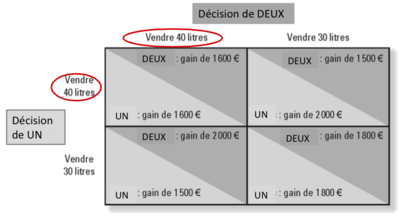
Le jeu oligopolistique UN et DEUX

Equilibre de non-coopération: (40L, 40L)

Optimum (pour les producteurs) → coopération: (30L, 30L)

La coopération dans un cadre dynamique

Avec le passage du temps et si on considère que le "jeu" entre les duopolistes se répète, on peut envisager la coopération comme plus stable, car les duopolistes se rendent compte des profits auxquels ils renoncent en trichant.

Tant que les firmes se soucient des profits futurs, elles décideront de renoncer au gain ponctuel résultant du non-respect de l’accord dans le cadre d’un jeu répété.

Lorsque UN triche, DEUX peut le “punir” par la cessation immédiate de la coopération et le retour à l’équilibre non-coopératif → punition CREDIBLE.

UN se rend compte qu’il a gagné un profit de triche de court terme mais perdu tous les profits de monopole futur....

La répétition du jeu sans date de fin, ou une incertitude, permet d’assurer un équilibre coopératif.

L'oligopole et le rôle de l'État

L'oligopole et le rôle de l'État

La coopération entre les membres de l’oligopole est désirable du point de vue des entreprises du secteur en question uniquement. Pour la société dans son ensemble, l’oligopole est indésirable car il conduit à une production trop basse et à des prix trop élevés.

La plupart des pays s’équipent d’un appareil législatif visant à empêcher les enfreintes à la concurrence par des cartels ou des ententes sur les prix.

Certaines lois sont plus souples que d’autres selon le pays.

Les économistes, de leur côté, ne sont pas toujours unanimes sur la manière de juger les restrictions à la concurrence et la nécessité de légiférer contre certaines pratiques.

États-Unis : le Sherman Antitrust Act

Loi votée déjà à la fin du XIXe siècle (1890) pour contrer le monopole de la

Standard Oil de la famille Rockfeller.

« Every contract, combination in the form of trust or otherwise, or conspiracy, in restraint of trade or commerce among the several States, or with foreign nations, is declared to be illegal.

Every person who shall make any contract or engage in any combination or conspiracy hereby declared to be illegal shall be deemed guilty of a felony, and, on conviction thereof, shall be punished by fine not exceeding $100,000,000 if a corporation, or, if any other person, $1,000,000, or by imprisonment not exceeding 10 years, or by both said punishments, in the discretion of the court. »

Le Sherman Act a été complété par le Clayton Act en 1914.

Europe : le Traité de Rome (art. 82)

Selon le Traité de Rome (1957), est incompatible avec le marché commun et interdit, dans la mesure où le commerce entre États membres est susceptible d’en être affecté, le fait pour une ou plusieurs entreprises d’exploiter de façon abusive une position dominante sur le marché commun ou dans une partie substantielle de celui-ci.

Ces pratiques abusives peuvent notamment consister à :

1. imposer de façon directe ou indirecte des prix d’achat ou de vente ou d’autres conditions de transaction non équitables ;
2. limiter la production, les débouchés ou le développement technique au préjudice des consommateurs ;
3. appliquer à l’égard de partenaires commerciaux des conditions inégales à des prestations équivalentes, en leur infligeant de ce fait un désavantage dans la concurrence ;
4. subordonner la conclusion de contrats à l’acceptation, par les partenaires, de prestations supplémentaires qui, par leur nature ou selon les usages commerciaux, n’ont pas de lien avec l’objet de ces contrats.

Suisse : la nouvelle LCart

La loi anti-trust en Suisse (de 1995, révisée en 2004) est fondée sur la notion d’abus (les accords anti-concurrentiels sont licites, seuls les abus sont illicites), alors qu’ailleurs (en Europe notamment) c’est le principe de l’interdiction qui prévaut.

Possibilité pour la Comco (Commission de la Concurrence) d’infliger des sanctions dès la première infraction (avant: seulement dans les cas de récidive).

La LCart prévoit un programme de clémence qui devrait inciter les entreprises à collaborer pour bénéficier d’une réduction de l’amende.

Des sanctions jusqu’à à 10% du chiffre d’affaire réalisé en Suisse au cours des trois dernières années.

LCart: l'abus de position dominante

« (...) Sont en particulier réputés illicites:

a) le refus d’entretenir des relations commerciales (p. ex. refus de livrer ou d’acheter des marchandises);

b) la discrimination de partenaires commerciaux en matière de prix ou d’autres conditions commerciales;

c) le fait d’imposer des prix ou d’autres conditions commerciales inéquitables;

d) la sous-enchère en matière de prix ou d’autres conditions commerciales, dirigée contre un concurrent déterminé;

e) la limitation de la production, des débouchés ou du développement technique;

f) le fait de subordonner la conclusion de contrats à la condition que les partenaires acceptent ou fournissent des prestations supplémentaires. »

Résumé

Les firmes en oligopole maximisent leur profit total en formant un cartel ou en agissant comme un monopole.

Si les membres du cartel prennent les décisions relatives à leur niveau de production de manière individuelle (pas de coopération), le résultat est une plus grande quantité et un prix plus bas comparé à la situation de monopole.

Plus il y a de firmes dans l’oligopole, plus les quantités et les prix se rapprochent des niveaux concurrentiels.

Le dilemme du prisonnier montre que la poursuite de l’intérêt individuel peut empêcher les individus de maintenir la coopération alors qu’elle est dans leur intérêt mutuel.

La logique du dilemme du prisonnier s’applique dans de nombreuses situations incluant la course à l’armement, la publicité, les ressources communes et les oligopoles.

Les décideurs politiques utilisent les lois sur la concurrence pour empêcher les oligopoles d’adopter des comportements qui réduisent la concurrence.

Source: Perloff, 2007

NB: MR = marginal revenu et MC = marginal cost

Annexes

• Universalis‎, Encyclopædia. “ÉQUILIBRE ÉCONOMIQUE.” Encyclopædia Universalis, www.universalis.fr/encyclopedie/equilibre-economique/10-l-equilibre-de-nash/.

Références