|
|
| Ligne 53 : |
Ligne 53 : |
| == La recette == | | == La recette == |
|
| |
|
| Le '''profit''' (<math>\pi</math>) d'une entreprise est calculé comme la différence entre la recette totale (<math>RT</math>) et le coût total (<math>CT</math>). Mathématiquement, cela s'exprime comme suit : | | Le profit (<math>\pi</math>) de l’entreprise est donné par la différence entre la recette totale (<math>RT</math>) et le coût total (<math>CT</math>). |
|
| |
|
| <math>\pi = RT - CT</math> | | Nous avons déjà analysé les fonctions de coût, mais pas encore les déterminants de la '''recette totale''' : <math>RT = Prix \times \text{Quantité}</math> |
|
| |
|
| La '''recette totale''' (<math>RT</math>) correspond au produit du prix (<math>P</math>) par la quantité (<math>q</math>) vendue, comme expliqué précédemment : | | La RT est proportionnelle à la quantité vendue (<math>q</math>) car, dans un marché compétitif, le prix est donné. |
|
| |
|
| <math>RT = P \times q</math> | | La '''recette moyenne''' (<math>RM</math>) nous dit quel est le revenu que l’entreprise fait en moyenne par unité vendue : <math>RM = \frac {RT}{\text{Quantité}} = \frac{Prix \times \text{Quantité}}{\text{Quantité}} = Prix</math> |
|
| |
|
| Le '''coût total''' (<math>CT</math>) représente la somme de tous les coûts engagés par l'entreprise pour produire et vendre ses biens ou services. Le coût total peut être divisé en deux composantes principales :
| | La '''recette marginale''' (<math>Rm</math>) nous dit quel est l’augmentation du revenu lorsque les quantités vendues (<math>q</math>) augmentent: |
|
| |
|
| <math>CT = \text{Coût fixe (CF)} + \text{Coût variable (CV)}</math>
| | <math>Rm = \frac {\Delta RT}{\Delta q}</math> (= <math>\frac {\partial RT}{\partial q}</math> pour des variations infinitésimales) |
| | | Pour les firmes concurrentielles, la recette marginale est égale au prix du bien : <math>Rm = \frac {\Delta RT}{\Delta q} = p</math> |
| Le '''coût fixe''' (<math>CF</math>) est indépendant de la quantité produite et vendue. Il inclut des éléments tels que les coûts de location des locaux, les salaires des employés administratifs, les dépenses en marketing, etc.
| |
| | |
| Le '''coût variable''' (<math>CV</math>) varie en fonction de la quantité produite et vendue. Il comprend des éléments tels que les coûts des matières premières, de la main-d'œuvre directe, de l'énergie, etc. En général, le coût variable est exprimé en fonction de la quantité produite (<math>q</math>), ce qui signifie que plus l'entreprise produit, plus le coût variable augmente.
| |
| | |
| En résumé, le profit (<math>\pi</math>) d'une entreprise est calculé en soustrayant le coût total (<math>CT</math>) de la recette totale (<math>RT</math>) :
| |
| | |
| <math>\pi = RT - CT</math>
| |
| | |
| avec <math>RT = P \times q</math>
| |
| | |
| et <math>CT = CF + CV</math>
| |
| | |
| Dans un marché compétitif, la '''recette totale''' (RT) est proportionnelle à la quantité vendue (q) car le prix est donné. La relation mathématique est exprimée par l'équation suivante :
| |
| | |
| <math>RT = Prix \times q</math>
| |
| | |
| Dans un marché en concurrence parfaite, chaque entreprise est un "price taker" (preneuse de prix) et ne peut pas influencer le prix de vente. Le prix est déterminé par les forces du marché, telles que l'offre et la demande, et est considéré comme donné pour chaque entreprise. Ainsi, lorsque l'entreprise vend une quantité donnée de produits, sa recette totale est simplement le produit du prix de vente par cette quantité.
| |
| | |
| Par exemple, si le prix d'un produit est de 10 euros et que l'entreprise vend 100 unités de ce produit, alors sa recette totale serait de :
| |
| | |
| <math>RT = 10 \times 100 = 1000</math>
| |
| | |
| Si l'entreprise vendait 200 unités du même produit au même prix, sa recette totale serait de :
| |
| | |
| <math>RT = 10 \times 200 = 2000</math>
| |
| | |
| Ainsi, dans un marché compétitif, l'entreprise peut augmenter sa recette totale en augmentant la quantité vendue, puisque le prix est donné et reste constant.
| |
| | |
| La '''recette moyenne''' (RM) représente le revenu moyen généré par l'entreprise par unité vendue. La recette moyenne est calculée en divisant la recette totale (RT) par la quantité vendue (q). Mathématiquement, cela s'exprime comme suit :
| |
| | |
| <math>RM = \frac{RT}{\text{Quantité}} = \frac{Prix \times \text{Quantité}}{\text{Quantité}} = Prix</math>
| |
| | |
| En simplifiant l'expression, nous obtenons que la recette moyenne (RM) est égale au prix (P). Dans un marché compétitif en concurrence parfaite, où le prix est donné et constant pour chaque unité vendue, la recette moyenne est égale au prix de vente. Cela signifie que le revenu moyen par unité vendue est égal au prix de vente. Il est important de noter que la recette moyenne (RM) peut varier d'une entreprise à une autre dans un marché en concurrence parfaite si différentes entreprises vendent à des prix différents. Cependant, pour une entreprise individuelle, la recette moyenne est égale au prix.
| |
| | |
| La recette marginale (Rm) représente l'augmentation de la recette totale (RT) lorsqu'il y a une augmentation d'une unité de la quantité vendue (q). La recette marginale est calculée en prenant le rapport de la variation de la recette totale (ΔRT) par la variation de la quantité vendue (Δq). Mathématiquement, cela s'exprime comme suit :
| |
| | |
| <math>Rm = \frac {\Delta RT}{\Delta q}</math> | |
| | |
| Dans le cas de variations infinitésimales, on peut utiliser la notation différentielle pour exprimer la recette marginale :
| |
| | |
| <math>Rm = \frac {\partial RT}{\partial q}</math> | |
| | |
| Pour les firmes en concurrence parfaite, où le prix (p) est donné et constant, la recette marginale est effectivement égale au prix du bien. Cela signifie que lorsque l'entreprise en concurrence parfaite augmente la quantité vendue d'une unité, la recette marginale est égale au prix de vente : | |
| | |
| <math>Rm = p</math> | |
| | |
| En d'autres termes, dans un marché en concurrence parfaite, chaque unité supplémentaire vendue rapporte à l'entreprise un montant égal au prix de vente. Cela découle de la condition d'atomicité du marché, où les entreprises sont de petites taille par rapport au marché et ne peuvent pas influencer le prix.
| |
|
| |
|
| == Le profit == | | == Le profit == |
|
| |
|
| Les deux composantes du profit dépendent de la quantité produite (q) : | | Les deux composantes du profit dépendent de la quantité produite : |
| | | :<math>\pi(q)=RT(q) - CT(q)</math> |
| Le '''profit''' (<math>\pi(q)</math>) à un niveau de production donné est calculé en soustrayant le coût total (<math>CT(q)</math>) de la recette totale (<math>RT(q)</math>) :
| | :<math>\pi(q) = p \times q - CF - CV(q)</math> (pour une entreprise concurrentielle) |
| <math>\pi(q) = RT(q) - CT(q)</math> | |
| | |
| Pour une entreprise en concurrence parfaite, la recette totale (<math>RT(q)</math>) est égale au produit du prix (<math>p</math>) par la quantité vendue (<math>q</math>) :
| |
| <math>RT(q) = p \times q</math>
| |
| | |
| Le '''coût total''' (<math>CT(q)</math>) comprend le coût fixe (<math>CF</math>) qui est indépendant de la quantité produite, ainsi que le coût variable (<math>CV(q)</math>) qui varie en fonction de la quantité produite :
| |
| <math>CT(q) = CF + CV(q)</math>
| |
| | |
| En résumé, pour une entreprise concurrentielle, le profit à un niveau de production donné est donné par :
| |
| | |
| <math>\pi(q) = p \times q - CF - CV(q)</math> | |
| | |
| où le prix (<math>p</math>) est donné par le marché, le coût fixe (<math>CF</math>) est indépendant de la quantité produite, et le coût variable (<math>CV(q)</math>) dépend de la quantité produite.
| |
| | |
| Le '''profit moyen''' (<math>\pi_M(q)</math>) à un niveau de production donné est calculé en soustrayant le coût moyen total (<math>CM(q)</math>) de la recette moyenne (<math>RM</math>). Mathématiquement, cela s'exprime comme suit :
| |
| | |
| <math>\pi_M(q) = RM - CM(q)</math>
| |
| | |
| Dans le cas d'une entreprise concurrentielle, la recette moyenne (<math>RM</math>) est égale au prix (<math>p</math>) et le coût moyen total (<math>CM(q)</math>) comprend le coût moyen fixe (<math>CFM</math>) qui est indépendant de la quantité produite, ainsi que le coût moyen variable (<math>CVM(q)</math>) qui dépend de la quantité produite. Donc, nous avons :
| |
| | |
| <math>\pi_M(q) = p - CFM - CVM(q)</math>
| |
| | |
| Cela signifie que le profit moyen par unité produite est égal à la différence entre le prix et les coûts moyens (fixes et variables) par unité produite.
| |
| | |
| Le '''profit margina'''l (<math>\pi_m(q)</math>) à un niveau de production donné est calculé en soustrayant le coût marginal (<math>Cm(q)</math>) de la recette marginale (<math>Rm</math>). Mathématiquement, cela s'exprime comme suit :
| |
| | |
| <math>\pi_m(q) = Rm - Cm(q)</math>
| |
| | |
| Dans le cas d'une entreprise concurrentielle, la recette marginale (<math>Rm</math>) est égale au prix (<math>p</math>) et le coût marginal (<math>Cm(q)</math>) représente l'augmentation du coût total lorsque la quantité produite augmente d'une unité. Ainsi, nous avons :
| |
| | |
| <math>\pi_m(q) = p - Cm(q)</math>
| |
| | |
| Cela signifie que le profit marginal par unité produite est égal à la différence entre le prix et le coût marginal par unité produite.
| |
| | |
| Pour maximiser le profit, il est nécessaire que le coût marginal (Cm) soit égal à la recette marginale (Rm). Cela se traduit mathématiquement par :
| |
| | |
| <math>\frac{\partial \pi}{\partial q} = \frac{\partial RT}{\partial q} - \frac{\partial CT}{\partial q} = Rm - Cm = p - Cm = 0</math>
| |
| | |
| Cette équation représente la condition de premier ordre (CPO) pour maximiser le profit. Elle indique que le profit est maximisé lorsque la recette marginale est égale au coût marginal.
| |
| | |
| En d'autres termes, à l'optimum, la recette marginale (Rm) est égale au prix (p), qui est également égal au coût marginal (Cm) :
| |
| | |
| <math>Rm = p = Cm</math>
| |
| | |
| Cette condition est essentielle dans le cadre de l'optimisation de la production et de la prise de décision de l'entreprise en termes de quantité produite. Elle permet d'identifier le niveau de production où l'entreprise maximise son profit, en équilibrant les revenus marginaux et les coûts marginaux.
| |
| | |
| == Maximisation du π : un exemple numérique ==
| |
| Prenons un exemple numérique pour illustrer la maximisation du profit avec une recette moyenne (RM) et une recette marginale (Rm) de 6 €. Supposons également que le prix (p) soit de 6 €.
| |
| | |
| Pour maximiser le profit, nous devons égaliser la recette marginale (Rm) au coût marginal (Cm). Dans cet exemple, puisque Rm = 6 €, nous devons trouver le niveau de production où le coût marginal est également de 6 €.
| |
|
| |
|
| Supposons que le coût marginal (Cm) soit de 4 € pour une certaine quantité produite. Dans ce cas, le profit est de :
| | Le profit moyen est : |
| | :<math>\pi_M(q) = RM - CM(q) = p - CFM - CVM(q)</math> |
|
| |
|
| <math>\pi = Rm - Cm = 6 , \text{€} - 4 , \text{€} = 2 , \text{€}</math> | | Le profit marginal est : |
| | :<math>\pi_m(q) = Rm - Cm(q) = p - Cm(q)</math> |
|
| |
|
| Cependant, si nous augmentons la quantité produite et que le coût marginal augmente à 6 €, le profit sera nul :
| | Le profit est maximisé quand le coût marginal est égal à la recette marginale : <math> max\pi(q) = RT(q) - CT(q)</math> |
|
| |
|
| <math>\pi = Rm - Cm = 6 , \text{€} - 6 , \text{€} = 0 , \text{€}</math> | | CPO (condition de premier ordre) : |
| | ::<math> \frac {\partial \pi}{\partial q} = \frac {\partial RT}{\partial q} - \frac {\partial CT}{\partial q} = Rm - Cm = p - Cm = 0</math> |
|
| |
|
| À partir de ce point, si nous continuons à augmenter la quantité produite, le coût marginal dépassera la recette marginale et le profit deviendra négatif. Par conséquent, le niveau de production qui maximise le profit est celui où Rm = p = Cm, c'est-à-dire lorsque la recette marginale, la recette moyenne et le prix sont tous de 6 €. | | À l’optimum <math>Rm = p = Cm</math> |
|
| |
|
| | == Maximisation du π : un exemple numérique == |
| [[Fichier:Maximisation du profit un exemple numérique 1.png|400px|vignette|centré|NB: P = 6 € => RM = Rm = 6 €]] | | [[Fichier:Maximisation du profit un exemple numérique 1.png|400px|vignette|centré|NB: P = 6 € => RM = Rm = 6 €]] |
|
| |
|
| == Maximisation du π : analyse graphique == | | == Maximisation du π : analyse graphique == |
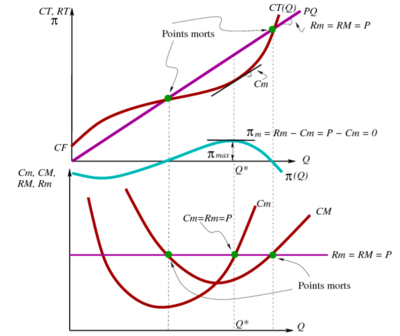
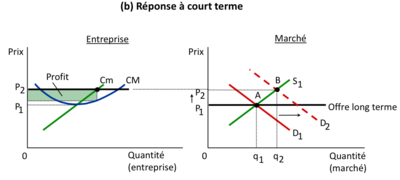
| L'analyse graphique de la maximisation du profit permet de visualiser le point où la différence entre la recette totale et le coût total est maximisée.
| | La firme décide de la quantité à produire de façon à maximiser ses profits et en raisonnant à la marge... |
| | |
| Sur un graphique, nous représentons généralement la quantité produite (<math>q</math>) sur l'axe des abscisses et la recette totale (<math>RT</math>) ainsi que le coût total (<math>CT</math>) sur l'axe des ordonnées.
| |
| | |
| La recette totale (<math>RT</math>) est représentée par une courbe croissante qui dépend de la quantité produite. Au fur et à mesure que la quantité produite augmente, la recette totale augmente également, mais à un taux décroissant. | |
| | |
| Le coût total (<math>CT</math>) est représenté par une courbe croissante qui dépend également de la quantité produite. À mesure que la quantité produite augmente, le coût total augmente, souvent à un taux croissant en raison des rendements marginaux décroissants.
| |
| | |
| Le profit (<math>\pi</math>) est représenté par la différence entre la recette totale (<math>RT</math>) et le coût total (<math>CT</math>), et il est donc représenté par la distance verticale entre les deux courbes.
| |
| | |
| Pour maximiser le profit, nous cherchons le point où la différence entre la recette totale et le coût total est maximale. Cela se produit lorsque la pente de la recette totale (<math>RT</math>) est égale à la pente du coût total (<math>CT</math>).
| |
| | |
| Géométriquement, cela correspond à trouver le point d'intersection ou de tangence entre les courbes de la recette totale (<math>RT</math>) et du coût total (<math>CT</math>).
| |
|
| |
|
| La quantité correspondante à ce point est notée <math>q^*</math> et représente le niveau de production qui maximise la différence entre la recette totale et le coût total, c'est-à-dire le profit.
| | <math>q^*</math> maximise la différence entre la recette totale et le coût total. |
|
| |
|
| [[Fichier:Maximisation du profit analyse graphique 1.png|400px|vignette|centré]] | | [[Fichier:Maximisation du profit analyse graphique 1.png|400px|vignette|centré]] |
| Ligne 202 : |
Ligne 97 : |
| == Cm versus CM == | | == Cm versus CM == |
|
| |
|
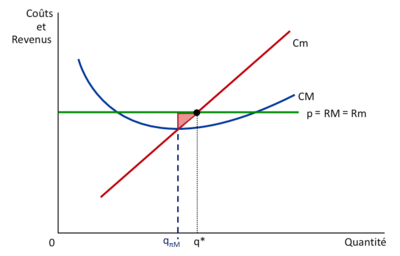
| si une entreprise se limite à produire la quantité <math>q_\pi M</math>, qui maximise le profit moyen, elle renonce à réaliser des bénéfices nets. Cela est dû au fait que le profit moyen est calculé en divisant le profit total par la quantité produite, ce qui peut masquer la réalité des bénéfices réels obtenus.
| | La firme décide de la quantité à produire de façon à maximiser ses profits en raisonnant à la marge... et non pas en moyenne. |
| | |
| Lorsque l'entreprise raisonne à la marge, elle cherche à maximiser son profit marginal (<math>Rm - Cm</math>) plutôt que son profit moyen. Le profit marginal est la différence entre la recette marginale (<math>Rm</math>) et le coût marginal (<math>Cm</math>). En maximisant le profit marginal, l'entreprise vise à trouver la quantité de production qui génère le plus grand bénéfice supplémentaire pour chaque unité supplémentaire produite.
| |
| | |
| Il est possible que la quantité qui maximise le profit moyen (<math>q_\pi M</math>) ne soit pas la même que celle qui maximise le profit net (total). La maximisation du profit net requiert l'égalité entre la recette marginale et le coût marginal (<math>Rm = Cm</math>), plutôt que l'égalité entre la recette moyenne et le coût moyen total (<math>RM = CM</math>) pour une quantité donnée.
| |
|
| |
|
| En conséquence, si l'entreprise se limite à produire la quantité qui maximise le profit moyen (<math>q_\pi M</math>), elle ne réalise pas de bénéfices nets supplémentaires au-delà de ce point. Pour obtenir des bénéfices nets, elle devrait augmenter la production jusqu'à ce que la recette marginale devienne inférieure au coût marginal.
| | Si l'entreprise se limite à produire <math>q_\pi M</math>, c’est-à-dire la quantité qui maximise le profit moyen, elle renonce à réaliser des bénéfices nets. |
|
| |
|
| [[Fichier:Cm versus CM analyse 1.png|400px|vignette|centré]] | | [[Fichier:Cm versus CM analyse 1.png|400px|vignette|centré]] |
|
| |
|
| == Maximisation du π : vue d'ensemble == | | == Maximisation du π : vue d'ensemble == |
|
| |
| Pour avoir une vue d'ensemble graphique de la maximisation du profit, nous pouvons représenter différentes courbes sur un graphique.
| |
|
| |
| Courbe de recette totale (<math>RT</math>) : Cette courbe montre comment la recette totale évolue en fonction de la quantité produite. Elle est généralement croissante, mais son taux d'augmentation peut diminuer à mesure que la quantité produite augmente en raison des effets de saturation du marché.
| |
|
| |
| Courbe de coût total (<math>CT</math>) : Cette courbe illustre comment le coût total varie en fonction de la quantité produite. Elle est également croissante, car le coût total augmente avec une augmentation de la production. Cependant, le taux d'augmentation peut varier en fonction de la technologie, des économies d'échelle, etc.
| |
|
| |
| Courbe de profit total (<math>\pi</math>) : Cette courbe montre comment le profit total évolue en fonction de la quantité produite. Elle est obtenue en soustrayant le coût total à la recette totale. Le profit total est généralement croissant jusqu'à un certain point, puis peut atteindre un maximum avant de diminuer si les coûts augmentent plus rapidement que les recettes à mesure que la production augmente.
| |
|
| |
| Courbe de profit marginal (<math>\pi_m</math>) : Cette courbe illustre comment le profit marginal varie en fonction de la quantité produite. Le profit marginal est la différence entre la recette marginale et le coût marginal. La courbe du profit marginal peut atteindre un maximum à un certain niveau de production, indiquant la quantité qui maximise le profit.
| |
|
| |
| En combinant ces courbes sur un graphique, nous pouvons identifier le niveau de production qui maximise le profit en trouvant le point où la courbe du profit total atteint son maximum ou en égalisant la recette marginale et le coût marginal. Cela nous donne une vue d'ensemble visuelle de la maximisation du profit dans le contexte de l'interaction entre la recette, les coûts et le niveau de production.
| |
|
| |
| [[Fichier:Maximisation du profit vue ensemble 1.png|400px|vignette|centré]] | | [[Fichier:Maximisation du profit vue ensemble 1.png|400px|vignette|centré]] |
|
| |
|
| == Profit == | | == Profit == |
|
| |
|
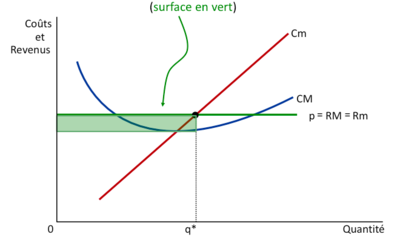
| Le profit maximum est donné par la différence entre la recette totale (RT) et le coût total (CT) au niveau de production correspondant à <math>q^*</math>. Mathématiquement, cela peut être exprimé comme suit : | | Le profit maximum est donné par la différence entre la RT et le CT au point <math>q^*</math>. |
| | | :<math>\pi = RT - CT = RM \times q - CM \times q = (RM - CM) \times q = (p - CM ) \times q</math> |
| <math>\pi = RT - CT = RM \times q - CM \times q = (RM - CM) \times q = (p - CM) \times q</math> | |
| | |
| où RM représente la recette moyenne, CM représente le coût moyen, p est le prix de vente et q est la quantité produite.
| |
| | |
| L'expression <math>(p - CM) \times q</math> montre que le profit est égal à la différence entre le prix de vente et le coût moyen, multipliée par la quantité produite. Cela signifie que le profit est déterminé par la différence entre le revenu généré par chaque unité vendue et le coût moyen associé à chaque unité produite.
| |
|
| |
|
| [[Fichier:Marché compétitif profit 1.png|400px|vignette|centré]] | | [[Fichier:Marché compétitif profit 1.png|400px|vignette|centré]] |
| Ligne 242 : |
Ligne 115 : |
| == Maximisation du π : un exemple analytique == | | == Maximisation du π : un exemple analytique == |
|
| |
|
| Pour déterminer la quantité qui maximise le profit de l'entreprise, nous allons utiliser la condition de premier ordre (CPO) en égalisant le coût marginal (Cm) au prix de marché (p).
| | Fonction de coût : <math> CT = 1 + 10q - q^2 + \frac {1}{3q^3}</math> |
| | |
| La fonction de coût est donnée par :
| |
| | |
| <math>CT = 1 + 10q - q^2 + \frac{1}{3q^3}</math> | |
| | |
| Le prix de marché est de 13, donc p = 13.
| |
| | |
| Pour trouver la quantité qui maximise le profit, nous égalisons Cm à p :
| |
| | |
| <math>Cm = 10 - 2q + q^2 = 13 = p</math>
| |
| | |
| Pour résoudre cette équation quadratique, nous pouvons utiliser la formule quadratique. En appliquant la formule, nous obtenons :
| |
|
| |
|
| <math>q = \frac{2 \pm \sqrt{4 - 4 \times 1 \times (-3)}}{2} = \frac{2 \pm \sqrt{16}}{2} = \frac{6}{2} = 3</math>
| | Déterminez quelle est la quantité qui maximise le profit de l’entreprise en sachant que le prix de marché p est égal à 13. |
|
| |
|
| Il y a deux solutions possibles pour q, mais nous choisissons la valeur positive, q = 3, car la quantité ne peut pas être négative.
| | CPO : <math>Cm = 10 - 2q + q^2 = 13 = p</math> |
|
| |
|
| Ainsi, la quantité qui maximise le profit de l'entreprise est de q = 3.
| | ::<math>q = \frac {2 \pm \sqrt {4 - 4 \times 1 \times (-3)}}{2} = \frac {2 \pm \sqrt {16}}{2} = {\frac {6}{2} > 0, ok \choose \frac {-2}{2} = -1 < 0, exclus}</math> |
|
| |
|
| = Offre de la firme de court et de long terme = | | = Offre de la firme de court et de long terme = |
| == La courbe d’offre de l’entreprise à court terme == | | == La courbe d’offre de l’entreprise à court terme == |
|
| |
|
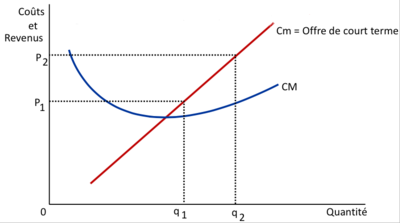
| A court terme, la courbe d'offre de l'entreprise est généralement représentée par la courbe du coût marginal (Cm). Cela signifie que l'entreprise offre des quantités de production correspondant aux niveaux où le coût marginal est égal ou inférieur au prix de marché.
| | La courbe d’offre de l’entreprise à court terme Coûts coïncide avec la fonction de coût marginal... |
| | |
| Le coût marginal représente le coût supplémentaire engendré par l'augmentation d'une unité de production. L'entreprise est incitée à augmenter sa production tant que le coût marginal est inférieur ou égal au prix de marché, car cela lui permet d'augmenter son profit. Une fois que le coût marginal dépasse le prix de marché, l'entreprise n'a plus d'incitation à augmenter sa production, car cela réduirait son profit.
| |
| | |
| Ainsi, la courbe d'offre de l'entreprise à court terme coïncide avec la courbe du coût marginal, représentant les quantités de production que l'entreprise est disposée à offrir à différents niveaux de prix, en fonction de ses coûts marginaux.
| |
|
| |
|
| [[Fichier:Courbe d’offre de l’entreprise à court terme 1.png|400px|vignette|centré]] | | [[Fichier:Courbe d’offre de l’entreprise à court terme 1.png|400px|vignette|centré]] |
|
| |
|
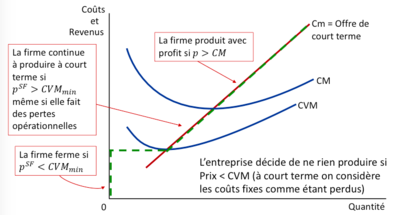
| == Décision de fermeture à court terme == | | == Décision de fermeture à court terme == |
| | | ... au dessus du CVM |
| La décision de fermeture à court terme pour une entreprise se produit lorsque le prix de marché descend en dessous du coût variable moyen (CVM). Le coût variable moyen représente le coût variable par unité produite. Lorsque le prix de marché est inférieur au CVM, cela signifie que l'entreprise ne peut pas couvrir ses coûts variables moyens avec les revenus générés par la vente de ses produits. Dans cette situation, l'entreprise subirait des pertes en continuant à produire et vendre. Dans de tels cas, l'entreprise peut prendre la décision de fermer temporairement ses activités à court terme. Cela signifie qu'elle cesse de produire et de vendre ses produits jusqu'à ce que les conditions du marché s'améliorent et que le prix de marché dépasse à nouveau le CVM. La décision de fermeture à court terme est une stratégie de gestion visant à minimiser les pertes en période de prix bas, où les coûts variables ne sont pas couverts. Cela permet à l'entreprise de réduire ses pertes et de se préparer à une reprise éventuelle du marché.
| |
|
| |
|
| [[Fichier:Décision de fermeture à court terme 1.png|400px|vignette|centré]] | | [[Fichier:Décision de fermeture à court terme 1.png|400px|vignette|centré]] |
| Ligne 281 : |
Ligne 137 : |
| L'entreprise pourrait décider de ne rien produire pendant une période donnée du fait des conditions courantes de marché. | | L'entreprise pourrait décider de ne rien produire pendant une période donnée du fait des conditions courantes de marché. |
|
| |
|
| La firme continue à produire si le profit qu'elle réalise en produisant une quantité non-nulle (<math>q^*</math>) est plus élevé que le profit (perte) qu'elle fait en arrêtant la production : | | La firme continue à produire si le profit qu'elle réalise en produisant une quantité non-nulle (q*) est plus élevé que le profit (perte) qu'elle fait en |
| | |
| <math>q = 0 \rightarrow \pi(0) = -CF</math>
| |
| | |
| <math>q = q^* \rightarrow \pi(q^) = pq^ - CV(q^*) - CF</math>
| |
| | |
| Cela signifie que lorsque la quantité produite est nulle (<math>q = 0</math>), le profit (<math>\pi</math>) est égal au coût fixe (<math>CF</math>) et donc l'entreprise subit une perte équivalente à son coût fixe.
| |
| | |
| Lorsque la quantité produite est égale à <math>q^*</math>, le profit est calculé comme suit :
| |
| | |
| <math>\pi(q^) = pq^ - CV(q^*) - CF</math>
| |
| | |
| Cela représente la recette totale <math>p \cdot q</math>) moins les coûts variables (<math>CV(q)</math>) et les coûts fixes (<math>CF</math>).
| |
| | |
| L'entreprise continue à produire tant que le profit réalisé en produisant une quantité non nulle (<math>q^*</math>) est supérieur à la perte subie en arrêtant complètement la production (<math>q = 0</math>). Cela signifie que si le profit réalisé en produisant est positif (supérieur à <math>CF</math>), l'entreprise a intérêt à continuer à produire. Sinon, elle peut envisager de suspendre temporairement sa production pour éviter de subir des pertes.
| |
| | |
| La décision de continuer ou d'arrêter la production dépendra donc de la comparaison entre les profits réalisés à différents niveaux de production et les pertes associées à l'arrêt de la production.
| |
| | |
| La firme décide de produire une quantité positive si le profit réalisé à cette quantité est supérieur à la perte subie en ne produisant rien. Cela peut être exprimé mathématiquement comme suit :
| |
| | |
| <math>\pi(q^\ast) > \pi(0)</math>
| |
| <math>pq^\ast > CV(q^\ast)</math>
| |
| <math>p > CVM(q^\ast)</math>
| |
| | |
| Ainsi, si le prix de marché (p) est supérieur au coût variable moyen (CVM) pour la quantité de production optimale (q*), l'entreprise a intérêt à produire une quantité positive.
| |
| | |
| Par contre, l'entreprise ferme lorsque la recette qu'elle aurait obtenue en produisant est inférieure au coût variable de production. Cela se produit lorsque le prix de marché (p) est inférieur au coût variable moyen (CVM), car cela signifie que l'entreprise ne peut pas couvrir ses coûts variables avec les revenus générés par la vente de ses produits.
| |
| | |
| En ce qui concerne la courbe d'offre de l'entreprise à court terme, elle correspond à la partie de la courbe du coût marginal qui se situe au-dessus du coût moyen variable (CMV). Cela signifie que l'entreprise est prête à offrir des quantités de production tant que le prix de marché couvre au moins les coûts variables associés à cette production. Au-dessus du coût moyen variable, l'entreprise peut générer un profit positif qui contribue à couvrir les coûts fixes et à générer un bénéfice net.
| |
|
| |
|
| En résumé, l'entreprise décide de produire une quantité positive lorsque le prix de marché dépasse le coût variable moyen (CVM), et elle ferme lorsque la recette potentielle de la production est inférieure au coût variable de production. La courbe d'offre de l'entreprise à court terme coïncide avec la partie de la courbe du coût marginal au-dessus du coût moyen variable.
| | arrêtant la production: |
|
| |
|
| Le seuil de fermeture peut être défini comme le niveau de prix (<math>p</math>) au-dessus duquel l'entreprise décide de continuer à produire, même si elle fait des pertes. Ce seuil de fermeture est déterminé par le coût variable moyen minimal (<math>CVM_{\min}</math>) nécessaire pour couvrir les coûts variables associés à la production.
| | :<math>q = 0</math> → <math>\pi(0) = -CF</math> |
| | :<math>q = q^\ast</math> → <math>\pi(q^\ast) = pq^\ast - CV(q^\ast) - CF</math> |
|
| |
|
| Lorsque le prix de marché (<math>p</math>) est supérieur au seuil de fermeture (<math>p^{(SF)}</math>), c'est-à-dire lorsque <math>p^{(SF)} > CVM_{\min}</math>, l'entreprise peut décider de continuer à produire même si elle subit des pertes. Cela peut être dû à divers facteurs tels que la volonté de maintenir la présence sur le marché, l'espoir d'une amélioration future des conditions ou d'autres considérations stratégiques.
| | La firme produit une quantité positive si <math>\pi(q^\ast) > \pi(0)</math> => si <math>pq^\ast > CV(q^\ast)</math> => si <math>p > CVM(q^\ast)</math> |
|
| |
|
| Dans ces situations, l'entreprise peut choisir de supporter temporairement des pertes afin de maintenir son activité et de préserver sa capacité de production. Elle peut espérer que les conditions du marché s'améliorent à l'avenir, ce qui lui permettra de générer des bénéfices une fois que le prix de marché sera à nouveau supérieur à son coût total moyen.
| | L'entreprise ferme si la recette qu’elle aurait obtenue en produisant est inférieure au coût variable de la production et la courbe d’offre de la firme à court terme est la partie de la courbe de coût marginal au-dessus du coût moyen variable. |
|
| |
|
| Cependant, il est important de noter que la décision de continuer à produire malgré les pertes dépend des circonstances spécifiques de chaque entreprise. Des facteurs tels que la situation financière, les capacités de gestion des risques et les perspectives du marché peuvent influencer la décision de continuer à produire même en situation de pertes.
| | On peut donc définir le seuil de fermeture comme le niveau de prix tel que : <math> p^{(SF)} > CVM_{min}</math> |
|
| |
|
| En résumé, le seuil de fermeture est déterminé par le niveau de prix (<math>p</math>) au-dessus duquel l'entreprise choisit de continuer à produire, même si elle subit des pertes. Cette décision peut être basée sur la volonté de maintenir une présence sur le marché et la perspective d'une amélioration future des conditions.
| | Tant que l’entreprise se trouve au-dessus du seuil de fermeture, elle a intérêt à continuer à produire, même si elle fait des pertes. |
|
| |
|
| [[Fichier:Décision de fermeture à court terme 2.png|400px|vignette|centré]] | | [[Fichier:Décision de fermeture à court terme 2.png|400px|vignette|centré]] |
| Ligne 327 : |
Ligne 156 : |
| == La courbe d’offre de l’entreprise à long terme == | | == La courbe d’offre de l’entreprise à long terme == |
|
| |
|
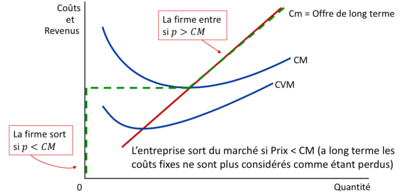
| La courbe d'offre de l'entreprise à long terme coïncide avec la portion de la fonction de coût marginal de long terme située au-dessus du coût moyen (CM). | | La courbe d’offre de l’entreprise à long terme coïncide avec la portion de la fonction de coût marginal de long terme au dessus du CM. |
| | |
| À long terme, les entreprises ont la possibilité d'ajuster leurs facteurs de production, y compris la taille de leurs installations et leur capacité de production. Elles peuvent entrer ou sortir du marché, ce qui leur permet de s'adapter aux conditions de demande et de concurrence.
| |
| | |
| La courbe d'offre de l'entreprise à long terme représente les quantités qu'une entreprise est prête à offrir à différents niveaux de prix une fois qu'elle a ajusté tous ses facteurs de production à long terme. Elle est généralement déterminée par la portion de la fonction de coût marginal de long terme qui se situe au-dessus du coût moyen.
| |
| | |
| Cette portion de la fonction de coût marginal de long terme au-dessus du coût moyen représente les niveaux de production où les coûts marginaux sont inférieurs aux coûts moyens. Cela signifie que l'entreprise peut produire à ces niveaux avec des coûts marginaux inférieurs à sa moyenne, ce qui lui permet de réaliser des bénéfices.
| |
| | |
| La courbe d'offre de l'entreprise à long terme est donc généralement positive et croissante, car l'entreprise est prête à offrir des quantités plus importantes à des prix plus élevés. Cependant, la forme précise de la courbe d'offre à long terme dépendra des caractéristiques spécifiques de l'industrie et des entreprises qui y opèrent.
| |
|
| |
|
| [[Fichier:Courbe d’offre de l’entreprise à long terme 1.png|400px|vignette|centré]] | | [[Fichier:Courbe d’offre de l’entreprise à long terme 1.png|400px|vignette|centré]] |
| Ligne 341 : |
Ligne 162 : |
| == Décision de sortir/entrer == | | == Décision de sortir/entrer == |
|
| |
|
| La fermeture et la sortie sont deux décisions distinctes prises par une entreprise en fonction de la durée et des implications financières. | | La fermeture renvoie à une décision de court terme de ne rien produire pendant une période donnée, tandis que la sortie fait référence à une décision de long terme de quitter le marché. |
| | |
| La fermeture est une décision de court terme dans laquelle l'entreprise cesse temporairement de produire pendant une période donnée. Cela peut être dû à des conditions défavorables du marché, une demande insuffisante ou d'autres facteurs temporaires. Lorsqu'une entreprise opte pour la fermeture temporaire, elle peut suspendre ses activités pour une période limitée dans l'espoir d'une amélioration future des conditions ou pour minimiser les pertes à court terme.
| |
| | |
| La sortie, en revanche, est une décision de long terme dans laquelle l'entreprise décide de quitter définitivement le marché. Cette décision est généralement prise lorsque l'entreprise est confrontée à des conditions économiques défavorables persistantes, une concurrence intense ou d'autres facteurs structurels qui rendent difficile la viabilité à long terme de l'entreprise sur ce marché. Lorsqu'une entreprise décide de sortir du marché, elle cesse de produire et se retire complètement de l'activité, liquidant souvent ses actifs et mettant fin à ses opérations dans cette industrie.
| |
| | |
| Lorsqu'une entreprise prend la décision de sortie, elle tient compte des coûts irrécouvrables (CF), qui sont tous les coûts déjà engagés et qui ne peuvent plus être récupérés. Ces coûts sont considérés comme des pertes permanentes et sont pris en compte dans l'évaluation de la décision de sortie. Cela peut inclure des investissements initiaux, des dépenses liées à l'infrastructure, des coûts de formation du personnel, etc. L'entreprise évalue si les bénéfices futurs potentiels sont suffisamment élevés pour compenser ces coûts irrécouvrables.
| |
|
| |
|
| En revanche, lors de la décision de fermeture temporaire, les coûts irrécouvrables ne sont généralement pas pris en compte car l'entreprise prévoit de reprendre ses activités à l'avenir et considère la fermeture comme une mesure temporaire pour faire face à des conditions difficiles à court terme.
| | La firme prend en compte les coûts irrécouvrables (= tout coût qui a déjà été engagé et qui ne peut plus être récupéré = CF) quand elle décide de sortir du marché, mais les ignore quand elle décide de fermer temporairement. |
|
| |
|
| '''A long terme, une firme prend la décision de quitter le marché si la recette totale qu'elle retirerait de la production est inférieure à ses coûts totaux'''. Mathématiquement, cela peut être exprimé comme suit :
| | À long terme, la firme quitte le marché si la recette qu’elle retirerait de la production est inférieure à ses coûts totaux : |
| | ::si <math>RT < CT</math> => si <math>\frac {RT}{q} < \frac {CT}{q}</math> => si <math>p < CM</math> |
|
| |
|
| Si <math>RT < CT</math>, alors <math>\frac{RT}{q} < \frac{CT}{q}</math>, où <math>q</math> représente la quantité produite.
| | À long terme, la firme entre sur le marché si la recette qu’elle retirerait de la production est supérieur à ses coûts totaux (= profits positifs): => si <math>RT > CT</math> => si <math> \frac {RT}{q} > \frac{CT}{q}</math> => si <math>p > CM</math>. |
|
| |
|
| Si nous divisons à la fois le numérateur et le dénominateur par <math>q</math>, nous obtenons :
| | La courbe d’offre de long terme est la portion de la courbe de coût marginal qui se situe au-dessus du coût moyen total. |
| | |
| <math>\frac{RT}{q} < \frac{CT}{q}</math>
| |
| | |
| Cela peut être simplifié en utilisant les notations de recette moyenne (<math>RM = \frac{RT}{q}</math>) et de coût moyen (<math>CM = \frac{CT}{q}</math>) :
| |
| | |
| <math>RM < CM</math>
| |
| | |
| En d'autres termes, si le prix de vente (p) est inférieur au coût moyen (CM), alors la recette moyenne (RM) est inférieure au coût moyen (CM). Cela signifie que l'entreprise ne peut pas couvrir ses coûts moyens par le prix de vente et réaliserait des pertes si elle continuait à produire. Ainsi, à long terme, une entreprise prend la décision de quitter le marché si le prix de vente est inférieur au coût moyen. Cette décision est basée sur la comparaison entre la recette moyenne et le coût moyen, ce qui indique si l'entreprise peut couvrir ses coûts et réaliser des bénéfices.
| |
| | |
| '''A long terme, une firme entre sur le marché si la recette totale qu'elle retirerait de la production est supérieure à ses coûts totaux''', ce qui se traduit par des profits positifs. La formulation correcte est la suivante :
| |
| | |
| Si <math>RT > CT</math>, alors <math>\frac{RT}{q} > \frac{CT}{q}</math>, où <math>q</math> représente la quantité produite.
| |
| | |
| Si nous divisons à la fois le numérateur et le dénominateur par <math>q</math>, nous obtenons :
| |
| | |
| <math>\frac{RT}{q} > \frac{CT}{q}</math>
| |
| | |
| Cela peut être simplifié en utilisant les notations de recette moyenne (<math>RM = \frac{RT}{q}</math>) et de coût moyen (<math>CM = \frac{CT}{q}</math>) :
| |
| | |
| <math>RM > CM</math>
| |
| | |
| En d'autres termes, si le prix de vente (p) est supérieur au coût moyen (CM), alors la recette moyenne (RM) est supérieure au coût moyen (CM). Cela signifie que l'entreprise peut couvrir ses coûts moyens par le prix de vente et réaliser des profits positifs si elle entre sur le marché. Ainsi, à long terme, une entreprise prend la décision d'entrer sur le marché si le prix de vente est supérieur au coût moyen. Cette décision est basée sur la comparaison entre la recette moyenne et le coût moyen, ce qui indique si l'entreprise peut couvrir ses coûts et réaliser des profits.
| |
| | |
| La courbe d'offre de long terme est généralement représentée par la portion de la courbe de coût marginal qui se situe au-dessus du coût moyen total (CMT). Le coût marginal (CM) représente le coût additionnel engendré par la production d'une unité supplémentaire. Le coût moyen total (CMT) quant à lui, correspond au coût total divisé par la quantité produite. Dans le long terme, les entreprises ont la flexibilité d'ajuster tous leurs facteurs de production, y compris la taille des installations et la capacité de production. Elles peuvent entrer ou sortir du marché, ajuster leur échelle de production et optimiser leurs coûts. La portion de la courbe de coût marginal située au-dessus du coût moyen total indique que les coûts marginaux sont inférieurs aux coûts moyens. Cela signifie que l'entreprise peut produire à ces niveaux de production avec des coûts marginaux inférieurs à sa moyenne, ce qui lui permet de réaliser des bénéfices. La courbe d'offre de long terme est donc généralement positive et croissante au-dessus du coût moyen total, car l'entreprise est prête à offrir des quantités plus importantes à des prix plus élevés, tout en restant rentable. Cependant, la forme exacte de la courbe d'offre de long terme dépendra des caractéristiques spécifiques de l'industrie et des entreprises qui y opèrent. | |
|
| |
|
| = Offre agrégée = | | = Offre agrégée = |
| == La courbe d’offre agrégée à court terme == | | == La courbe d’offre agrégée à court terme == |
|
| |
|
| A court terme, la courbe d'offre agrégée est donnée par la somme horizontale des courbes d'offre individuelles des entreprises. Cela signifie que la courbe d'offre agrégée représente la quantité totale offerte sur le marché à chaque niveau de prix, en prenant en compte toutes les entreprises présentes.
| | La courbe d’offre agrégée est donnée par la somme (horizontale) des courbes d’offre individuelles des entreprises. |
| | |
| À court terme, on suppose généralement un nombre fixe d'entreprises sur le marché, sans entrée ou sortie d'entreprises. Dans cette situation, la courbe d'offre agrégée peut être obtenue en additionnant les quantités offertes par chaque entreprise à chaque niveau de prix.
| |
| | |
| Mathématiquement, la courbe d'offre agrégée à court terme peut être représentée par :
| |
| | |
| <math>Q^s = Q_1^s + Q_2^s + Q_3^s + \ldots + Q_n^s</math>
| |
| | |
| où <math>Q^s</math> représente la quantité totale offerte, <math>Q_1^s</math>, <math>Q_2^s</math>, <math>Q_3^s</math>, ..., <math>Q_n^s</math> représentent les quantités offertes par chaque entreprise individuelle.
| |
|
| |
|
| Cette courbe d'offre agrégée à court terme illustre la quantité totale que toutes les entreprises sont prêtes à offrir sur le marché à chaque niveau de prix. Elle est influencée par des facteurs tels que les coûts de production, les prix des intrants, la technologie, les conditions du marché, etc.
| | Avec un nombre fixe d’entreprises (sans sortie ou entrée d’entreprises dans le marché), c’est-à-dire à court terme , on a que : |
|
| |
|
| [[Fichier:Courbe d’offre agrégée à court terme ECP1.png|400px|vignette|centré]] | | [[Fichier:Courbe d’offre agrégée à court terme ECP1.png|400px|vignette|centré]] |
| Ligne 400 : |
Ligne 184 : |
| == La courbe d’offre agrégée à long terme == | | == La courbe d’offre agrégée à long terme == |
|
| |
|
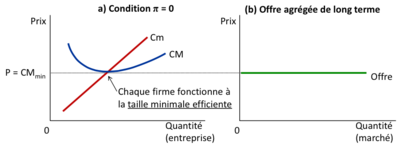
| A long terme, la courbe d'offre agrégée est déterminée par le comportement des entreprises sur le marché en fonction de la relation entre le prix (P) et le coût moyen (CM).
| | Comme on vient de voir à la fin de la section précédente, dans le long terme les entreprises décident d'entrer sur (quitter) le marché si le prix est plus grand (plus petit) que le coût moyen. |
|
| |
|
| Si le prix de marché (P) est supérieur au coût moyen (CM), cela signifie que les entreprises réalisent des profits économiques positifs. Dans cette situation, de nouvelles entreprises sont incitées à entrer sur le marché afin de profiter de ces profits. Cela se traduit par un déplacement de la courbe d'offre agrégée vers la droite, ce qui signifie que la quantité offerte sur le marché augmente. Parallèlement, le prix tend à baisser jusqu'à ce qu'un nouvel équilibre soit atteint où le prix (p) est égal au coût moyen (CM). Cela représente une situation d'équilibre à long terme sur le marché où les profits économiques sont nuls. | | :Si <math>P > CM</math>, des nouvelles entreprises rentrent sur le marché car elles font des profits économiques positifs, la courbe d’offre agrégée se déplace vers la droite, et le prix tombe, jusqu’à ce qu’on retrouve un équilibre où <math>p = CM</math>. |
| | :Si <math>P < CM</math>, des entreprises sortent du marché car elles font des profits économiques négatifs, la courbe d’offre agrégée se contracte, et le prix augmente, jusqu’à ce que <math>p = CM</math>. |
|
| |
|
| Inversement, si le prix de marché (P) est inférieur au coût moyen (CM), cela signifie que les entreprises subissent des pertes économiques. Dans cette situation, certaines entreprises peuvent décider de quitter le marché afin de réduire leurs pertes. Cela entraîne un retrait de l'offre sur le marché, ce qui fait augmenter le prix jusqu'à ce qu'un nouvel équilibre soit atteint où le prix (p) est égal au coût moyen (CM). Encore une fois, cela représente une situation d'équilibre à long terme où les profits économiques sont nuls.
| | Donc, à l’équilibre de long terme <math>p = CM</math>, les profits sont nuls et la courbe d'offre du marché est horizontale. |
|
| |
|
| Ainsi, à long terme, la courbe d'offre agrégée se déplace et s'ajuste en réponse aux conditions de marché, en fonction de la relation entre le prix et le coût moyen. L'entrée ou la sortie d'entreprises sur le marché permet d'atteindre un équilibre où le prix correspond au coût moyen, ce qui garantit l'absence de profits économiques à long terme.
| | Mais alors qu’est-ce qui se passe avec notre ‘fameux’ raisonnement à la marge qui nous dit que l’ équilibre de maximisation des profit se trouve où <math>p = Cm</math> ? |
|
| |
|
| A l'équilibre de long terme sur le marché, le prix (p) est égal au coût moyen (CM) des entreprises. Cela signifie que les profits économiques sont nuls, car les entreprises ne réalisent ni bénéfices ni pertes.
| | La courbe d’offre agrégée à long terme est horizontale (dans la plupart des cas). Le nombre de firmes présentes sur le marché s'ajuste de façon telle que chacune maximise ses profits de long terme au point où les profits économiques sont nuls. Des entreprises entrent et sortent du marché afin d’offrir n’importe quelle quantité demandée par le marché a un prix égal au minimum du CM (= EME). |
| | |
| À cet équilibre, la courbe d'offre du marché devient horizontale, ce qui indique que la quantité offerte reste constante à différents niveaux de prix. Cela est dû au fait que toutes les entreprises présentes sur le marché produisent au coût moyen et n'ont pas de motivation supplémentaire pour ajuster leur offre en réponse à des variations de prix.
| |
| | |
| Cette horizontalité de la courbe d'offre du marché à long terme est une caractéristique clé de la concurrence parfaite. Dans ce type de marché, toutes les entreprises sont des preneuses de prix, ce qui signifie qu'elles n'ont pas le pouvoir de fixer le prix, mais doivent accepter le prix déterminé par les forces du marché. Par conséquent, l'équilibre à long terme est caractérisé par des profits nuls et une courbe d'offre horizontale.
| |
| | |
| Dans la théorie de la concurrence parfaite, le raisonnement à la marge indique que les entreprises maximisent leurs profits en produisant à un niveau où le coût marginal (Cm) est égal au prix de marché (p). C'est en effet le point où les bénéfices sont maximisés. Cependant, il est important de distinguer entre l'équilibre de maximisation des profits à court terme et l'équilibre à long terme sur le marché. À court terme, les entreprises peuvent réaliser des profits économiques positifs ou négatifs en fonction de la différence entre le prix de marché et le coût moyen variable (CVM). Dans cet état, les entreprises peuvent entrer ou sortir du marché pour ajuster leur offre et maximiser leurs profits. La courbe d'offre agrégée à court terme peut avoir une pente positive en raison de ces ajustements. À long terme, cependant, les entreprises ont le temps d'ajuster tous leurs facteurs de production, y compris leur taille et leur capacité, afin de maximiser leurs profits. Cela implique l'entrée ou la sortie d'entreprises du marché jusqu'à ce que les profits économiques soient nuls. L'équilibre à long terme est atteint lorsque le prix de marché est égal au coût moyen (CM). À cet équilibre, la courbe d'offre agrégée devient horizontale, car toutes les entreprises produisent au coût moyen. Dans cet état d'équilibre à long terme, chaque entreprise maximise ses profits en produisant au point où le coût marginal est égal au coût moyen (Cm = CM), mais les profits économiques sont nuls. Les entreprises sont incitées à offrir n'importe quelle quantité demandée par le marché à un prix égal au minimum du coût moyen (EME). Ainsi, l'équilibre de maximisation des profits à court terme (Cm = p) et l'équilibre de long terme sans profits économiques (CM = p) sont deux concepts distincts, mais ils sont tous deux pertinents pour comprendre le fonctionnement du marché dans le cadre de la concurrence parfaite.
| |
|
| |
|
| [[Fichier:Coucourbe d’offre agrégée à long terme 1.png|400px|vignette|centré]] | | [[Fichier:Coucourbe d’offre agrégée à long terme 1.png|400px|vignette|centré]] |
| Ligne 420 : |
Ligne 199 : |
| == Profits économiques nuls : intuition == | | == Profits économiques nuls : intuition == |
|
| |
|
| Lorsqu'on parle de profits économiques nuls à long terme, cela signifie que les revenus obtenus par les propriétaires d'entreprise sont équivalents à leur coût d'opportunité. Les profits économiques tiennent compte du coût d'opportunité dans l'évaluation des rémunérations des facteurs de production, tandis que les profits comptables n'en tiennent pas compte.
| | Rappel : des profits nuls à long terme ne veulent pas dire que les propriétaires n’ont pas de revenu, mais simplement que leur revenu à long terme est identique à leur coût d’opportunité. |
| | |
| Il est important de faire la distinction entre les profits économiques et les profits comptables. Les profits économiques prennent en compte tous les coûts, y compris le coût d'opportunité des ressources utilisées dans l'entreprise. Le coût d'opportunité représente la valeur de la meilleure alternative abandonnée lorsqu'une ressource est utilisée dans une activité particulière.
| |
| | |
| D'autre part, les profits comptables ne tiennent généralement pas compte du coût d'opportunité. Ils sont basés sur les revenus et les dépenses comptables réels et ne prennent pas en compte les coûts implicites ou les revenus que les propriétaires pourraient obtenir s'ils utilisaient leurs ressources ailleurs.
| |
|
| |
|
| Ainsi, il est tout à fait possible d'avoir un profit comptable positif alors que les profits économiques sont nuls. Cela peut se produire lorsque les revenus générés par l'entreprise couvrent les coûts explicites (dépenses réelles) mais ne prennent pas en compte les coûts implicites, tels que le coût d'opportunité du capital investi par les propriétaires.
| | À l’équilibre de profit nul, la recette de la firme doit rémunérer les propriétaires pour le temps et l’argent qu’ils dépensent à faire fonctionner leur entreprise. |
|
| |
|
| En somme, les profits économiques nuls à long terme indiquent que les revenus des propriétaires d'entreprise sont équivalents à leur coût d'opportunité, tandis que les profits comptables peuvent être positifs en raison de la manière dont ils sont calculés et ne tiennent pas compte de tous les coûts implicites.
| | Un profit économique nul est tout à fait compatible avec un profit comptable positif car le profit économique tient compte du coût d’opportunité dans l’évaluation des rémunérations des facteurs et que le profit comptable n’en tient pas compte. |
|
| |
|
| == Courbe d’offre de long terme croissante == | | == Courbe d’offre de long terme croissante == |
|
| |
|
| La courbe d'offre à long terme peut avoir une pente positive en raison de certaines caractéristiques spécifiques des facteurs de production et de l'entrée de nouvelles entreprises sur le marché.
| | Pourquoi la courbe d’offre à long terme a aussi parfois une pente positive? |
| | |
| Une des raisons pour lesquelles la courbe d'offre à long terme peut avoir une pente positive est la disponibilité limitée de certaines ressources ou facteurs de production. Par exemple, dans le cas de terres agricoles, il peut y avoir une quantité limitée de terres fertiles disponibles. À long terme, lorsque de nouvelles entreprises agricoles entrent sur le marché, elles peuvent être contraintes d'utiliser des terres moins productives qui ont des coûts de production plus élevés. Cela peut se traduire par des fonctions de coûts croissantes pour ces entreprises, car elles ont besoin de dépenser plus pour obtenir une quantité donnée de production.
| |
|
| |
|
| En outre, l'entrée de nouvelles entreprises sur le marché peut également conduire à une diminution de la productivité marginale des facteurs de production. Au fur et à mesure que de plus en plus d'entreprises entrent sur le marché, les ressources peuvent être utilisées de manière moins efficace et moins productive. Cela peut entraîner des coûts de production plus élevés pour les entreprises supplémentaires, ce qui se traduit par une courbe d'offre à long terme avec une pente positive.
| | Certaines ressources (facteurs de production) sont disponibles seulement dans des quantités limitées même à long terme (exemple: terre agricole). |
|
| |
|
| Il est important de noter que la courbe d'offre à long terme sera toujours plus élastique que la courbe d'offre à court terme, c'est-à-dire qu'elle sera plus réactive aux variations de prix. Cela est dû au fait que la flexibilité des entreprises à long terme leur permet d'ajuster leurs facteurs de production de manière plus complète pour répondre à la demande du marché. En revanche, à court terme, les entreprises ont des contraintes plus limitées pour ajuster leur production et leurs coûts.
| | Au fur et à mesure que des nouvelles entreprises entrent dans le marché leur productivité peut être de moins en moins grande. Ces nouvelles entreprises ont des fonctions de coût de plus en plus élevées (la terre agricole est de moins en moins productive). La condition de profits nuls est établie sur l’entreprise marginale. |
|
| |
|
| En résumé, la courbe d'offre à long terme peut avoir une pente positive en raison de facteurs tels que la disponibilité limitée de certaines ressources et la diminution de la productivité marginale des facteurs de production. Cela reflète les conditions spécifiques du marché et montre que l'entrée de nouvelles entreprises peut entraîner des coûts de production plus élevés, ce qui se traduit par une courbe d'offre à long terme avec une pente positive.
| | La courbe d’offre à long terme aura une pente positive, mais toujours plus grande que la courbe d’offre à court terme (= au coût marginal sans libre entrée et sortie des entreprises). En d’autres termes, la courbe d’offre de longue période est toujours plus élastique de la courbe d’offre de courte période. |
|
| |
|
| == Mécanisme d’ajustement : court versus long terme == | | == Mécanisme d’ajustement : court versus long terme == |
| Le mécanisme d'ajustement diffère entre le court terme et le long terme dans le cadre de la théorie de la concurrence parfaite.
| |
|
| |
| * Au court terme, les entreprises sont souvent confrontées à des contraintes d'ajustement de leurs facteurs de production. Elles peuvent ajuster leur production en modifiant la quantité de travail et de capital utilisée, mais il peut y avoir des limitations en termes de flexibilité. Par exemple, l'ajustement des capacités de production ou des installations peut prendre du temps et être coûteux. Dans ce cas, les entreprises peuvent réagir aux changements de demande ou de prix en ajustant leur offre via la variation de la quantité produite à court terme. La courbe d'offre à court terme est généralement caractérisée par une pente positive, car les entreprises sont contraintes par leurs coûts fixes et ne peuvent pas ajuster complètement leur production en réponse à des variations de prix.
| |
| * Au long terme, les entreprises ont une plus grande flexibilité pour ajuster leurs facteurs de production. Elles peuvent entrer sur le marché en créant de nouvelles entreprises ou en augmentant leur capacité de production existante, ou elles peuvent sortir du marché en fermant leurs activités. À long terme, les entreprises peuvent ajuster pleinement leurs facteurs de production pour maximiser leurs profits. Si les profits économiques sont positifs, de nouvelles entreprises seront incitées à entrer sur le marché, augmentant ainsi l'offre. Si les profits économiques sont négatifs, certaines entreprises peuvent choisir de sortir du marché, réduisant ainsi l'offre. Ce processus d'entrée et de sortie d'entreprises conduit à un ajustement de l'offre à long terme. À l'équilibre à long terme, les profits économiques sont nuls et la courbe d'offre à long terme est horizontale.
| |
|
| |
| En résumé, au court terme, les entreprises ajustent leur offre en modifiant la quantité produite, tandis qu'au long terme, elles ajustent leur offre en entrant ou en sortant du marché et en ajustant pleinement leurs facteurs de production.
| |
|
| |
|
| [[Fichier:Mécanisme d’ajustement court versus long terme 1.png|400px|vignette|centré]] | | [[Fichier:Mécanisme d’ajustement court versus long terme 1.png|400px|vignette|centré]] |
|
| |
|
| lorsque le marché fait face à un choc exogène positif de la demande, cela se traduit par une augmentation de la demande pour le bien ou le service. Cette augmentation de la demande entraîne une hausse du prix sur le marché.
| | Choc exogène positif de demande → hausse du prix → <math>p > CM</math> → <math>\pi > 0</math>. |
| | |
| Lorsque le prix de marché (p) est supérieur au coût moyen (CM), les entreprises réalisent des profits économiques positifs. Cela signifie que les revenus obtenus par les entreprises dépassent leurs coûts moyens de production. Ces profits économiques positifs sont représentés par l'expression <math>\pi > 0</math>, où <math>\pi</math> représente le profit.
| |
| | |
| Le choc exogène positif de la demande crée une opportunité pour les entreprises de réaliser des bénéfices en répondant à la demande accrue. Les entreprises peuvent ajuster leur offre en augmentant leur quantité produite pour répondre à la demande supplémentaire à un prix plus élevé. Cela leur permet de générer des profits économiques positifs.
| |
| | |
| Il est important de noter que ces bénéfices ne sont généralement pas permanents et peuvent diminuer à mesure que d'autres entreprises entrent sur le marché en réponse aux profits économiques. Cette entrée d'entreprises supplémentaires augmente l'offre et peut exercer une pression à la baisse sur les prix, réduisant ainsi les profits économiques à long terme.
| |
| | |
| En résumé, un choc exogène positif de la demande qui entraîne une hausse du prix sur le marché peut conduire à des profits économiques positifs pour les entreprises. Cependant, ces profits peuvent être temporaire et s'atténuer à long terme avec l'entrée de nouvelles entreprises sur le marché.
| |
|
| |
|
| [[Fichier:Mécanisme d’ajustement court versus long terme 2.png|400px|vignette|centré]] | | [[Fichier:Mécanisme d’ajustement court versus long terme 2.png|400px|vignette|centré]] |
|
| |
|
| Lorsque les entreprises réalisent des profits économiques positifs à court terme, cela attire généralement l'entrée de nouvelles entreprises sur le marché. Les profits économiques positifs sont un signal pour les entrepreneurs et les investisseurs qu'il y a une opportunité de réaliser des bénéfices en produisant et en offrant le bien ou le service en question.
| | Le profit économique de court terme attire des nouvelles entreprises dans le marché. |
| | |
| Lorsque les profits économiques sont élevés, cela incite les entrepreneurs à entrer sur le marché afin de tirer parti de cette situation favorable. Les nouvelles entreprises espèrent également pouvoir bénéficier des mêmes conditions de profitabilité que les entreprises déjà présentes.
| |
| | |
| L'entrée de nouvelles entreprises augmente l'offre sur le marché, ce qui peut potentiellement exercer une pression à la baisse sur les prix. Cela peut réduire les profits économiques à court terme pour les entreprises existantes, car elles doivent partager le marché avec de nouveaux concurrents.
| |
| | |
| Cependant, il est important de noter que l'entrée de nouvelles entreprises n'est pas immédiate et peut prendre du temps en raison des contraintes liées à la création et à la croissance d'une entreprise. De plus, la dynamique de l'entrée de nouvelles entreprises dépend également des barrières à l'entrée spécifiques au marché en question.
| |
| | |
| En résumé, lorsque les entreprises réalisent des profits économiques positifs à court terme, cela crée une incitation pour de nouvelles entreprises à entrer sur le marché et à profiter de cette situation. Cela peut entraîner une augmentation de l'offre et une éventuelle diminution des profits économiques à court terme pour les entreprises existantes.
| |
|
| |
|
| [[Fichier:Mécanisme d’ajustement court versus long terme 3.png|400px|vignette|centré]] | | [[Fichier:Mécanisme d’ajustement court versus long terme 3.png|400px|vignette|centré]] |
Les entreprises en concurrence parfaite
Lectures
En analysant le comportement des entreprises et les déterminants de l’offre de celles-ci sur le marché on distingue entre deux types de structure de marché :
- Les marchés compétitifs où on trouve un grand nombre d’entreprises et chaque entreprise individuellement n’a pas d’impact sur le prix ;
- Les marchés non compétitifs où les entreprises ont du pouvoir de marché et en changeant leur niveau de production (ventes) elles affectent les prix sur les marchés.
Dans ce chapitre nous nous concentrons sur les marchés compétitifs en examinant le rôle joué par les fonctions de coût de production des entreprises dans les décisions de produire ou ne pas produire et, si oui, quelles quantités. Dans les chapitres suivants nous allons analyser les principales formes de marché non-concurrentiel.
Un marché compétitif est un marché où il y a une infinité de vendeurs et acheteurs et où chacun d’entre eux a donc une part de marché infiniment petite (la taille de chacun est toute petite par rapport à la dimension du marché). Aucun agent économique n'est donc en mesure d’influencer le prix du marché en modifiant les quantités achetées ou vendues.
On peut également définir un marché compétitif comme étant un marché où :
- le bien vendu est homogène (pas trop de différence entre les producteurs) ;
- il y a un grand nombre d’acheteurs et des vendeurs ;
- il y a libre entrée et sortie des acheteurs et vendeurs sur le marché.
Le résultant de ces trois conditions étant toujours qu'aucun acheteur ni vendeur pris individuellement ne peut influencer le prix sur le marché. Les actions d’un vendeur ou d’un acheteur isolé sur le marché ont un impact négligeable sur le prix et tous sont des ‘preneurs de prix’ (price takers).
Maximisation du profit
La recette
Le profit ( ) de l’entreprise est donné par la différence entre la recette totale (
) de l’entreprise est donné par la différence entre la recette totale ( ) et le coût total (
) et le coût total ( ).
).
Nous avons déjà analysé les fonctions de coût, mais pas encore les déterminants de la recette totale : 
La RT est proportionnelle à la quantité vendue ( ) car, dans un marché compétitif, le prix est donné.
) car, dans un marché compétitif, le prix est donné.
La recette moyenne ( ) nous dit quel est le revenu que l’entreprise fait en moyenne par unité vendue :
) nous dit quel est le revenu que l’entreprise fait en moyenne par unité vendue : 
La recette marginale ( ) nous dit quel est l’augmentation du revenu lorsque les quantités vendues (
) nous dit quel est l’augmentation du revenu lorsque les quantités vendues ( ) augmentent:
) augmentent:
 (=
(=  pour des variations infinitésimales)
Pour les firmes concurrentielles, la recette marginale est égale au prix du bien :
pour des variations infinitésimales)
Pour les firmes concurrentielles, la recette marginale est égale au prix du bien : 
Le profit
Les deux composantes du profit dépendent de la quantité produite :

 (pour une entreprise concurrentielle)
(pour une entreprise concurrentielle)
Le profit moyen est :

Le profit marginal est :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi_m(q) = Rm - Cm(q) = p - Cm(q)}
Le profit est maximisé quand le coût marginal est égal à la recette marginale : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle max\pi(q) = RT(q) - CT(q)}
CPO (condition de premier ordre) :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {\partial \pi}{\partial q} = \frac {\partial RT}{\partial q} - \frac {\partial CT}{\partial q} = Rm - Cm = p - Cm = 0}
À l’optimum Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Rm = p = Cm}
Maximisation du π : un exemple numérique

NB: P = 6 € => RM = Rm = 6 €
Maximisation du π : analyse graphique
La firme décide de la quantité à produire de façon à maximiser ses profits et en raisonnant à la marge...
Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*}
maximise la différence entre la recette totale et le coût total.
Cm versus CM
La firme décide de la quantité à produire de façon à maximiser ses profits en raisonnant à la marge... et non pas en moyenne.
Si l'entreprise se limite à produire Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q_\pi M}
, c’est-à-dire la quantité qui maximise le profit moyen, elle renonce à réaliser des bénéfices nets.
Maximisation du π : vue d'ensemble
Profit
Le profit maximum est donné par la différence entre la RT et le CT au point Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*}
.
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi = RT - CT = RM \times q - CM \times q = (RM - CM) \times q = (p - CM ) \times q}
Maximisation du π : un exemple analytique
Fonction de coût : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CT = 1 + 10q - q^2 + \frac {1}{3q^3}}
Déterminez quelle est la quantité qui maximise le profit de l’entreprise en sachant que le prix de marché p est égal à 13.
CPO : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Cm = 10 - 2q + q^2 = 13 = p}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q = \frac {2 \pm \sqrt {4 - 4 \times 1 \times (-3)}}{2} = \frac {2 \pm \sqrt {16}}{2} = {\frac {6}{2} > 0, ok \choose \frac {-2}{2} = -1 < 0, exclus}}
Offre de la firme de court et de long terme
La courbe d’offre de l’entreprise à court terme
La courbe d’offre de l’entreprise à court terme Coûts coïncide avec la fonction de coût marginal...
Décision de fermeture à court terme
... au dessus du CVM
L'entreprise pourrait décider de ne rien produire pendant une période donnée du fait des conditions courantes de marché.
La firme continue à produire si le profit qu'elle réalise en produisant une quantité non-nulle (q*) est plus élevé que le profit (perte) qu'elle fait en
arrêtant la production:
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q = 0}
→ Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi(0) = -CF}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q = q^\ast}
→ Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi(q^\ast) = pq^\ast - CV(q^\ast) - CF}
La firme produit une quantité positive si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi(q^\ast) > \pi(0)}
=> si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle pq^\ast > CV(q^\ast)}
=> si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p > CVM(q^\ast)}
L'entreprise ferme si la recette qu’elle aurait obtenue en produisant est inférieure au coût variable de la production et la courbe d’offre de la firme à court terme est la partie de la courbe de coût marginal au-dessus du coût moyen variable.
On peut donc définir le seuil de fermeture comme le niveau de prix tel que : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p^{(SF)} > CVM_{min}}
Tant que l’entreprise se trouve au-dessus du seuil de fermeture, elle a intérêt à continuer à produire, même si elle fait des pertes.
La courbe d’offre de l’entreprise à long terme
La courbe d’offre de l’entreprise à long terme coïncide avec la portion de la fonction de coût marginal de long terme au dessus du CM.
Décision de sortir/entrer
La fermeture renvoie à une décision de court terme de ne rien produire pendant une période donnée, tandis que la sortie fait référence à une décision de long terme de quitter le marché.
La firme prend en compte les coûts irrécouvrables (= tout coût qui a déjà été engagé et qui ne peut plus être récupéré = CF) quand elle décide de sortir du marché, mais les ignore quand elle décide de fermer temporairement.
À long terme, la firme quitte le marché si la recette qu’elle retirerait de la production est inférieure à ses coûts totaux :
- si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RT < CT}
=> si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {RT}{q} < \frac {CT}{q}}
=> si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p < CM}
À long terme, la firme entre sur le marché si la recette qu’elle retirerait de la production est supérieur à ses coûts totaux (= profits positifs): => si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RT > CT}
=> si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {RT}{q} > \frac{CT}{q}}
=> si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p > CM}
.
La courbe d’offre de long terme est la portion de la courbe de coût marginal qui se situe au-dessus du coût moyen total.
Offre agrégée
La courbe d’offre agrégée à court terme
La courbe d’offre agrégée est donnée par la somme (horizontale) des courbes d’offre individuelles des entreprises.
Avec un nombre fixe d’entreprises (sans sortie ou entrée d’entreprises dans le marché), c’est-à-dire à court terme , on a que :
La courbe d’offre agrégée à long terme
Comme on vient de voir à la fin de la section précédente, dans le long terme les entreprises décident d'entrer sur (quitter) le marché si le prix est plus grand (plus petit) que le coût moyen.
- Si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle P > CM}
, des nouvelles entreprises rentrent sur le marché car elles font des profits économiques positifs, la courbe d’offre agrégée se déplace vers la droite, et le prix tombe, jusqu’à ce qu’on retrouve un équilibre où Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p = CM}
.
- Si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle P < CM}
, des entreprises sortent du marché car elles font des profits économiques négatifs, la courbe d’offre agrégée se contracte, et le prix augmente, jusqu’à ce que
 .
.
Donc, à l’équilibre de long terme  , les profits sont nuls et la courbe d'offre du marché est horizontale.
, les profits sont nuls et la courbe d'offre du marché est horizontale.
Mais alors qu’est-ce qui se passe avec notre ‘fameux’ raisonnement à la marge qui nous dit que l’ équilibre de maximisation des profit se trouve où  ?
?
La courbe d’offre agrégée à long terme est horizontale (dans la plupart des cas). Le nombre de firmes présentes sur le marché s'ajuste de façon telle que chacune maximise ses profits de long terme au point où les profits économiques sont nuls. Des entreprises entrent et sortent du marché afin d’offrir n’importe quelle quantité demandée par le marché a un prix égal au minimum du CM (= EME).
Profits économiques nuls : intuition
Rappel : des profits nuls à long terme ne veulent pas dire que les propriétaires n’ont pas de revenu, mais simplement que leur revenu à long terme est identique à leur coût d’opportunité.
À l’équilibre de profit nul, la recette de la firme doit rémunérer les propriétaires pour le temps et l’argent qu’ils dépensent à faire fonctionner leur entreprise.
Un profit économique nul est tout à fait compatible avec un profit comptable positif car le profit économique tient compte du coût d’opportunité dans l’évaluation des rémunérations des facteurs et que le profit comptable n’en tient pas compte.
Courbe d’offre de long terme croissante
Pourquoi la courbe d’offre à long terme a aussi parfois une pente positive?
Certaines ressources (facteurs de production) sont disponibles seulement dans des quantités limitées même à long terme (exemple: terre agricole).
Au fur et à mesure que des nouvelles entreprises entrent dans le marché leur productivité peut être de moins en moins grande. Ces nouvelles entreprises ont des fonctions de coût de plus en plus élevées (la terre agricole est de moins en moins productive). La condition de profits nuls est établie sur l’entreprise marginale.
La courbe d’offre à long terme aura une pente positive, mais toujours plus grande que la courbe d’offre à court terme (= au coût marginal sans libre entrée et sortie des entreprises). En d’autres termes, la courbe d’offre de longue période est toujours plus élastique de la courbe d’offre de courte période.
Mécanisme d’ajustement : court versus long terme
Choc exogène positif de demande → hausse du prix →  →
→  .
.
Le profit économique de court terme attire des nouvelles entreprises dans le marché.
Résumé
Le revenu total d’une entreprise sur un marché compétitif est proportionnel aux quantités produites (car le prix est donné). Le prix du bien est identique à son revenu moyen et marginal.
Une entreprise maximise ses profits en choisissant la quantité produite telle que le coût marginal est identique au revenu marginal (= prix) et donc la courbe d’offre de l’entreprise est donné par son coût marginal.
Dans le court terme quand une entreprise ne peut pas récupérer ses coûts fixes, l’entreprises décide de fermer temporairement ses opérations si le prix est inférieur au coût variable moyen.
Dans le long terme, l’entreprise récupère les coûts fixes et variables (pas de coûts perdus), et donc elle sort du marché seulement si le prix est inférieur au coût moyen.
Dans le long terme, avec l’entrée et sortie des entreprises, les profits des entreprises sont égales à zéro et elles produisent à leur EME. Si il y a de l’ hétérogénéité dans les fonctions de coût des entreprises certaines pourraient faire des profits positifs.
Annexes
Références