« Les entreprises en concurrence parfaite » : différence entre les versions
Aucun résumé des modifications |
|||
| (46 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
Basé sur un cours de Federica Sbergami<ref>[https://www.unige.ch/gsem/en/research/faculty/all/federica-sbergami/ Page personnelle de Federica Sbergami sur le site de l'Université de Genève]</ref><ref>[https://www.unine.ch/irene/home/equipe/federica_sbergami.html Page personnelle de Federica Sbergami sur le site de l'Université de Neuchâtel]</ref><ref>[https://www.researchgate.net/scientific-contributions/14836393_Federica_Sbergami Page personnelle de Federica Sbergami sur Research Gate]</ref> | |||
{{Translations | {{Translations | ||
| en = | | en = Firms in competitive markets | ||
| es = Las empresas en perfecta competencia | | es = Las empresas en perfecta competencia | ||
| it = Imprese in concorrenza perfetta | |||
| pt = Firmas em concorrência perfeita | |||
| de = Unternehmen im vollkommenen Wettbewerb | |||
}} | }} | ||
= | {{hidden | ||
|[[Introduction à la microéconomie]] | |||
|[[Principes et concepts de la microéconomie]] ● [[Approche méthodologiques au cours d'introduction à la microéconomie]] ● [[Les forces du marché : l'offre et la demande]] ● [[Les élasticités et ses applications]] ● [[Offre, demande et politiques gouvernementales]] ● [[Surplus du consommateur et du producteur]] ● [[Les externalités et le rôle de l'État]] ● [[Principes et Dilemmes des Biens Publics dans l'Économie de Marché]] ● [[Les coûts de production]] ● [[Les entreprises en concurrence parfaite]] ● [[Les entreprises en monopole]] ● [[Concurrence monopolistique]] ● [[Oligopole]] ● [[Contrainte et préférences du consommateur]] ● [[Choix du consommateur]] ● [[Les problèmes d'information et les choix publics]] | |||
|headerstyle=background:#ffffff | |||
|style=text-align:center; | |||
}} | |||
L'analyse des structures de marché en économie révèle deux types principaux : les marchés compétitifs et les marchés non compétitifs. Dans les marchés compétitifs, on trouve un grand nombre d'entreprises, où chacune a peu ou pas d'influence sur le prix du marché. Ces entreprises sont considérées comme des "priseurs de prix", acceptant le prix déterminé par le marché. Le rôle des fonctions de coût de production est crucial dans ces marchés, influençant fortement les décisions des entreprises en matière de production et les quantités produites. Ces décisions sont basées sur la maximisation du profit, où les entreprises cherchent à équilibrer les coûts et les revenus. L'équilibre du marché est atteint lorsque l'offre globale rencontre la demande globale, déterminant ainsi le prix du marché. | |||
En contraste, les marchés non compétitifs sont caractérisés par la présence d'entreprises ayant un pouvoir de marché significatif. Cela leur permet d'influencer les prix en ajustant leur niveau de production. Ces marchés comprennent des structures telles que les monopoles, où un seul vendeur domine, les oligopoles, caractérisés par quelques entreprises influentes, et la concurrence monopolistique, où plusieurs entreprises vendent des produits différenciés. Dans ces marchés, les entreprises ont la capacité d'affecter les prix sur le marché, contrairement aux marchés compétitifs où le prix est un résultat de l'équilibre entre l'offre et la demande. | |||
La notion de marché compétitif en économie est centrée sur l'idée d'une concurrence parfaite, où la structure du marché se définit par plusieurs caractéristiques distinctes. Dans un tel marché, on trouve une infinité de vendeurs et d'acheteurs, chacun ayant une part de marché extrêmement réduite. Cette configuration implique que la taille de chaque acteur économique est insignifiante par rapport à la taille totale du marché. En conséquence, aucun vendeur ou acheteur n'est en mesure d'influencer le prix du marché par ses actions individuelles, que ce soit en modifiant les quantités achetées ou vendues. | |||
Un marché compétitif se caractérise également par trois conditions principales. Premièrement, le bien vendu sur ce marché est homogène, signifiant qu'il y a peu ou pas de différence entre les produits offerts par différents producteurs. Cette homogénéité garantit que les consommateurs ne privilégient pas un vendeur par rapport à un autre en raison de la qualité ou des caractéristiques du produit. | |||
Deuxièmement, la présence d'un grand nombre d'acheteurs et de vendeurs est cruciale. Cette multiplicité d'acteurs garantit que l'influence individuelle de chaque vendeur ou acheteur sur le prix du marché est minime, voire négligeable. | |||
Troisièmement, un marché compétitif se caractérise par une libre entrée et sortie des acteurs sur le marché. Cela signifie qu'il n'existe pas de barrières significatives empêchant de nouveaux vendeurs ou acheteurs de participer au marché ou les acteurs existants de le quitter. | |||
Le résultat de ces conditions est qu'aucun acteur, qu'il soit acheteur ou vendeur, ne peut influencer le prix du marché. Dans ce contexte, tous les participants sont des 'preneurs de prix' (price takers), acceptant le prix du marché tel qu'il est déterminé par les forces globales de l'offre et de la demande. Ce modèle de marché est souvent utilisé comme idéal théorique pour analyser et comparer d'autres structures de marché moins compétitives, où certains acteurs peuvent exercer une influence significative sur les prix. | |||
= Maximisation du profit = | |||
La maximisation du profit est un concept central en économie et en gestion d'entreprise, représentant l'objectif principal des entreprises dans une économie de marché. Cette notion se fonde sur l'effort des entreprises pour obtenir la plus grande différence positive possible entre leurs revenus et leurs coûts. | |||
Les revenus totaux d'une entreprise sont déterminés par le volume de ses ventes et le prix de ses produits ou services. Les entreprises s'efforcent d'accroître ces revenus en augmentant soit la quantité de produits vendus, soit le prix de ces produits, ou les deux. Parallèlement, elles doivent gérer leurs coûts totaux, qui incluent à la fois les coûts fixes, tels que le loyer et les salaires, qui ne changent pas quelle que soit la production, et les coûts variables, qui varient en fonction du niveau de production, comme les matières premières. | |||
Le profit est la différence entre les revenus totaux et les coûts totaux. Une entreprise maximise son profit en trouvant le point où cette différence est maximale. Cette recherche de maximisation du profit influence toutes les décisions clés de l'entreprise, y compris les stratégies de production, de tarification, d'investissement et de marketing. Les décisions sont souvent prises sur la base d'une analyse marginale, qui examine l'impact sur les revenus et les coûts d'une augmentation ou d'une diminution de l'unité de production ou de vente. L'objectif est de continuer la production jusqu'à ce que le coût de production d'une unité supplémentaire soit égal au revenu généré par cette unité. | |||
Le contexte du marché joue un rôle crucial dans la capacité d'une entreprise à maximiser ses profits. Dans un marché hautement concurrentiel, par exemple, les entreprises peuvent être limitées dans leur capacité à fixer des prix élevés, tandis que dans des marchés moins concurrentiels, comme les monopoles, elles peuvent avoir plus de liberté pour augmenter leurs profits. | |||
== La recette == | |||
Dans un marché compétitif, la | Le profit (<math>\pi</math>) d'une entreprise est la différence entre sa recette totale (<math>RT</math>) et son coût total (<math>CT</math>). La recette totale est calculée comme le produit du prix par la quantité vendue, c'est-à-dire <math>RT = \text{Prix} \times \text{Quantité}</math>. Dans un marché compétitif, où le prix est déterminé par le marché et est donc constant pour chaque entreprise, la recette totale est directement proportionnelle à la quantité vendue (<math>q</math>). | ||
<math>RT = Prix \times | La recette moyenne (<math>RM</math>) indique le revenu qu’une entreprise réalise en moyenne par unité vendue. Elle est calculée comme <math>RM = \frac{RT}{\text{Quantité}}</math>. Puisque <math>RT = \text{Prix} \times \text{Quantité}</math>, la recette moyenne se simplifie en <math>RM = \text{Prix}</math>. Cela signifie que, dans un marché compétitif, la recette moyenne est égale au prix du produit. | ||
La recette marginale (<math>Rm</math>) est un concept clé pour comprendre comment les variations dans les quantités vendues affectent la recette totale. Elle est définie comme l'augmentation de la recette totale résultant de la vente d'une unité supplémentaire. Mathématiquement, cela se traduit par <math>Rm = \frac{\Delta RT}{\Delta q}</math>, ou, pour des variations infiniment petites, <math>Rm = \frac{\partial RT}{\partial q}</math>. Dans un marché compétitif, où le prix est constant, la recette marginale est égale au prix du bien, donc <math>Rm = \frac{\Delta RT}{\Delta q} = p</math>. | |||
En somme, dans un marché compétitif, la structure de prix fixe et uniforme simplifie considérablement le calcul des recettes. L'égalité de la recette marginale et du prix est un élément crucial qui influence la décision de l’entreprise concernant la quantité à produire pour maximiser son profit. | |||
== Le profit == | == Le profit == | ||
Le profit (<math>\pi</math>) d'une entreprise dépend de la quantité (<math>q</math>) produite. Pour une entreprise opérant dans un marché concurrentiel, le profit peut être exprimé comme la différence entre la recette totale (RT) et le coût total (CT) en fonction de la quantité, soit : | |||
Le | |||
<math>\pi(q) = RT(q) - CT(q)</math> | <math>\pi(q) = RT(q) - CT(q)</math> | ||
<math>\pi(q) = p \times q - CF - CV(q)</math> | <math>\pi(q) = p \times q - CF - CV(q)</math> | ||
où <math>p</math> est le prix du bien, <math>CF</math> représente les coûts fixes et <math>CV(q)</math> les coûts variables en fonction de la quantité. | |||
Le profit moyen (<math>\pi_M</math>) est la différence entre la recette moyenne (RM) et le coût moyen (CM) en fonction de la quantité : | |||
<math>\pi_M(q) = RM - CM(q) = p - CFM - CVM(q)</math> | |||
Le | Le profit marginal (<math>\pi_m</math>) est la différence entre la recette marginale (Rm) et le coût marginal (Cm) en fonction de la quantité : | ||
<math>\pi_m(q) = Rm - Cm(q) = p - Cm(q)</math> | |||
<math>\ | Le profit est maximisé lorsque le coût marginal est égal à la recette marginale. Ceci est exprimé par la condition de maximisation du profit : | ||
<math>\text{max} \pi(q) = RT(q) - CT(q)</math> | |||
La condition de premier ordre (CPO) pour maximiser le profit est que la dérivée première du profit par rapport à la quantité doit être égale à zéro. Mathématiquement, cela s'exprime comme suit : | |||
<math>\frac {\partial \pi}{\partial q} = \frac {\partial RT}{\partial q} - \frac {\partial CT}{\partial q} = Rm - Cm = p - Cm = 0</math> | |||
<math> | À l'optimum, la recette marginale (<math>Rm</math>), qui est égale au prix (<math>p</math>), est égale au coût marginal (<math>Cm</math>). Cette égalité est fondamentale dans la théorie de la production et de la maximisation du profit dans un contexte de concurrence parfaite. | ||
== Maximisation du π : un exemple numérique == | |||
L'exemple numérique fourni dans le tableau démontre comment une entreprise détermine le niveau de production qui maximise son profit. Dans cet exemple, l'entreprise vend son produit à un prix fixe de 6 euros par litre, ce qui se reflète dans la recette totale qui augmente de 6 euros pour chaque litre supplémentaire vendu. La ligne du coût total indique que l'entreprise a des coûts initiaux même sans production, qui pourraient être des coûts fixes tels que le loyer ou les salaires, et que le coût de production de chaque litre supplémentaire augmente, probablement en raison de l'augmentation des coûts variables.[[Fichier:Maximisation du profit un exemple numérique 1.png|400px|vignette|centré|NB: P = 6 € => RM = Rm = 6 €]]En observant la progression du profit total, on constate qu'il augmente avec chaque litre produit jusqu'à la production de 4 ou 5 litres, après quoi le profit commence à diminuer. Ce phénomène suggère que, bien que l'entreprise continue à recevoir 6 euros pour chaque litre supplémentaire (comme l'indique la recette marginale constante), les coûts de production de chaque litre supplémentaire augmentent à un rythme plus rapide, ce qui est évident dans les chiffres croissants du coût marginal. | |||
Le profit marginal, qui est l'augmentation du profit total résultant de la vente d'une unité supplémentaire, commence à décliner après la production de 5 litres, devenant négatif au-delà de ce point. Cela signifie que la production de plus de 5 litres réduit le profit global de l'entreprise, car le coût de production de ces litres supplémentaires est supérieur au revenu qu'ils génèrent. | |||
La maximisation du profit se produit lorsque le profit marginal est égal à zéro, ce qui se produit à 5 litres dans cet exemple. À ce niveau, le coût marginal, l'augmentation du coût total due à la production d'un litre supplémentaire, est exactement égal à la recette marginale, ce qui indique que l'entreprise ne gagne ni ne perd de profit supplémentaire sur le dernier litre produit. Selon la condition de premier ordre pour la maximisation du profit, c'est à ce point que l'entreprise devrait arrêter d'augmenter sa production pour maximiser son profit. | |||
En résumé, cet exemple illustre clairement la relation entre la recette marginale, le coût marginal et la maximisation du profit. Il démontre également que pour maximiser son profit, une entreprise dans un marché compétitif doit produire jusqu'à ce que le coût marginal de production égale la recette marginale obtenue de la vente d'une unité supplémentaire, et c'est à ce point que le profit total est maximisé. | |||
== Maximisation du π : analyse graphique == | |||
La maximisation du profit (<math>\pi</math>) par une entreprise peut être illustrée de manière graphique, ce qui permet de visualiser comment les décisions de production sont prises en fonction de la logique marginale. | |||
Dans un graphique typique, la quantité produite est placée sur l'axe horizontal (l'axe des abscisses), tandis que la recette totale (RT), le coût total (CT), et le profit sont placés sur l'axe vertical (l'axe des ordonnées). La recette totale est généralement représentée par une ligne droite qui commence à l'origine (si le prix est constant), car la recette totale est simplement le prix multiplié par la quantité. Le coût total commence généralement au-dessus de l'origine, représentant les coûts fixes, et courbe vers le haut à mesure que la quantité augmente, reflétant l'augmentation des coûts variables. | |||
La quantité qui maximise le profit, notée <math>q^*</math>, est là où l'écart entre la recette totale et le coût total est le plus grand. Graphiquement, c'est le point où la pente de la recette totale (qui est la recette marginale, Rm) est égale à la pente du coût total (qui est le coût marginal, Cm). À ce point, toute augmentation supplémentaire de la quantité produite ne ferait qu'ajouter autant de coûts que de revenus, ne contribuant ainsi pas au profit. | |||
Sur le graphique, la ligne de recette marginale coupe la ligne de coût marginal exactement à ce point optimal <math>q^*</math>. Avant ce point, la recette marginale excède le coût marginal, ce qui signifie que la production d'une unité supplémentaire ajoute plus au revenu qu'elle n'ajoute aux coûts, et donc le profit augmente. Après ce point, le coût marginal excède la recette marginale, donc la production d'une unité supplémentaire coûte plus qu'elle ne rapporte en termes de revenu, et le profit diminue. | |||
<math> | La décision de la firme de produire la quantité <math>q^*</math> reflète donc la logique marginale : continuer à produire tant que le revenu supplémentaire (Rm) est supérieur au coût supplémentaire (Cm) et s'arrêter là où ils sont égaux. C'est la quintessence de la maximisation du profit dans la théorie économique classique, et elle est souvent représentée dans un graphique par la tangence de la courbe de recette totale avec la courbe de coût total. | ||
[[Fichier:Maximisation du profit analyse graphique 1.png|400px|vignette|centré]] | |||
Ce graphique illustre l'analyse graphique de la maximisation du profit pour une entreprise dans un marché compétitif. | |||
Le graphique montre deux lignes principales : une ligne horizontale verte représentant le prix (<math>p</math>), qui est également la recette moyenne (<math>RM</math>) et la recette marginale (<math>Rm</math>), et une ligne rouge ascendante représentant le coût marginal (<math>Cm</math>) en fonction de la quantité produite. | |||
Point de Maximisation du Profit (<math>q^*</math>) : Sur ce graphique, le point de maximisation du profit, noté <math>q^*</math>, est là où la ligne de coût marginal (<math>Cm</math>) croise la ligne de recette marginale (<math>Rm</math>). C'est le niveau de production où la recette supplémentaire générée par la vente d'une unité supplémentaire est exactement égale au coût supplémentaire de la production de cette unité. À ce point, l'entreprise maximise son profit, car toute production supplémentaire au-delà de <math>q^*</math> entraînerait des coûts marginaux supérieurs aux recettes marginales, réduisant ainsi le profit. | |||
Recette et Coût Marginal : Le fait que la ligne de recette marginale soit horizontale indique que le prix de vente du produit reste constant, indépendamment de la quantité vendue, ce qui est typique d'une entreprise en concurrence parfaite. Le coût marginal, cependant, augmente avec la quantité, indiquant que la production de chaque unité supplémentaire coûte plus cher que la précédente. | |||
Zones de Profit : La zone ombrée entre les quantités <math>q_1</math> et <math>q^*</math> représente le profit total réalisé par l'entreprise. C'est la différence entre la recette totale et le coût total pour cette plage de production. | |||
<math> | Le graphique démontre clairement l'importance du coût marginal et de la recette marginale dans la prise de décision pour une entreprise compétitive. La règle de maximisation du profit est suivie lorsque l'entreprise produit à un niveau où le coût marginal est égal à la recette marginale. Produire moins que <math>q^*</math> signifierait que l'entreprise ne profite pas pleinement de sa capacité à générer du profit, tandis que produire plus que <math>q^*</math> signifierait que l'entreprise subirait des coûts marginaux qui réduisent le profit global. | ||
Il est également important de noter que si le coût marginal était inférieur à la recette marginale au-delà de <math>q^*</math>, l'entreprise pourrait augmenter sa production pour augmenter son profit. Inversement, si le coût marginal augmente brusquement ou si le prix du marché diminue, cela pourrait conduire à une réduction de la quantité optimale de production. | |||
Cet exemple graphique sert de modèle de base pour comprendre la prise de décision dans les entreprises compétitives, en assumant que les conditions de marché sont constantes et que l'entreprise est un preneur de prix, sans pouvoir d'influence sur le prix du marché. | |||
== | == Cm versus CM == | ||
L'entreprise cherche à maximiser ses profits en se focalisant sur les coûts et recettes marginaux plutôt que sur les moyennes. Le raisonnement à la marge implique la considération des coûts et des bénéfices supplémentaires liés à la production et à la vente d'une unité supplémentaire. | |||
Le coût marginal (<math>Cm</math>) représente le coût de production d'une unité supplémentaire de bien ou de service. Il est crucial dans la prise de décision car si le revenu supplémentaire (recette marginale) généré par la vente de cette unité est supérieur au coût marginal de sa production, l'entreprise augmente son profit en produisant cette unité supplémentaire. | |||
En revanche, le coût moyen (<math>CM</math>) représente le coût total divisé par le nombre d'unités produites. Il donne une indication du coût par unité mais ne reflète pas nécessairement les coûts liés à la production d'une unité supplémentaire. | |||
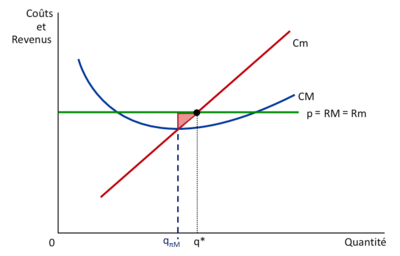
Si une entreprise se concentre uniquement sur la maximisation du profit moyen, noté <math>q_{\pi M}</math>, et s'arrête de produire à ce niveau, elle pourrait manquer l'opportunité de réaliser des bénéfices supplémentaires. La quantité qui maximise le profit moyen n'est pas nécessairement la même que celle qui maximise le profit total. En effet, tant que le coût marginal est inférieur à la recette marginale, l'entreprise peut augmenter son profit en augmentant sa production. | |||
L'objectif est donc de trouver le point où le coût marginal est égal à la recette marginale, ce qui est la condition pour maximiser le profit total. Arrêter la production au point où le profit moyen est maximisé pourrait signifier que l'entreprise ne produit pas suffisamment pour atteindre le point où le profit total est à son apogée. Cela peut être visualisé sur un graphique où le profit total continue d'augmenter jusqu'au point où le coût marginal croise la recette marginale, même si le profit moyen a déjà atteint son maximum à un niveau inférieur de production. | |||
[[Fichier:Cm versus CM analyse 1.png|400px|vignette|centré]] | |||
Ce graphique représente les courbes de coût et de revenu d'une entreprise, qui sont essentielles à la compréhension de la prise de décisions en matière de production pour maximiser le profit. On y voit trois courbes distinctes : la courbe de coût moyen (<math>CM</math>), la courbe de coût marginal (<math>Cm</math>) et une ligne horizontale qui représente à la fois le prix (<math>p</math>), la recette moyenne (<math>RM</math>) et la recette marginale (<math>Rm</math>), qui sont identiques dans un marché parfaitement concurrentiel où le prix est constant indépendamment de la quantité vendue. | |||
Le point où la courbe de coût marginal coupe la ligne de prix (et donc la recette marginale), noté <math>q^*</math>, est le niveau de production qui maximise le profit. À ce point, le coût supplémentaire de production d'une unité supplémentaire (<math>Cm</math>) est exactement égal au revenu supplémentaire que l'entreprise reçoit pour cette unité (<math>Rm</math>). Si l'entreprise produit plus ou moins que <math>q^*</math>, elle ne maximise pas ses profits : produire moins signifierait ne pas profiter de tous les revenus supplémentaires possibles, tandis que produire plus augmenterait les coûts plus rapidement que les revenus. | |||
La courbe de coût moyen (<math>CM</math>) atteint généralement son minimum avant d'augmenter à nouveau, ce qui est dû aux économies d'échelle et ensuite aux déséconomies d'échelle. Le point où le <math>CM</math> est le plus bas n'est pas le point qui maximise les profits, bien qu'il soit souvent interprété à tort comme tel. Ce point est noté <math>q_{\pi M}</math> sur le graphique et représente la quantité qui maximise le profit moyen, pas le profit total. Si une entreprise choisissait de produire à <math>q_{\pi M}</math>, elle produirait là où le coût moyen par unité est le plus bas, mais cela ne prend pas en compte les bénéfices marginaux de la production de quantités supplémentaires jusqu'à <math>q^*</math>. | |||
En conclusion, l'analyse graphique montre clairement pourquoi une entreprise devrait se concentrer sur les coûts et les revenus marginaux lors de la prise de décisions de production. L'objectif n'est pas de minimiser le coût moyen ou de maximiser le profit moyen, mais plutôt de trouver le point où le coût marginal de production d'une unité supplémentaire est égal au revenu supplémentaire généré par la vente de cette unité, ce qui se produit au niveau de production <math>q^*</math>. C'est à ce niveau que le profit total de l'entreprise est maximisé. | |||
== Maximisation du π : vue d'ensemble == | |||
Le graphique présenté offre une vue d'ensemble complexe et détaillée de la maximisation du profit (<math>\pi</math>) dans le cadre de la théorie économique de la firme. Plusieurs courbes clés sont représentées pour illustrer les différentes dimensions des coûts et des recettes d'une entreprise. | |||
[[Fichier:Maximisation du profit vue ensemble 1.png|400px|vignette|centré]] | |||
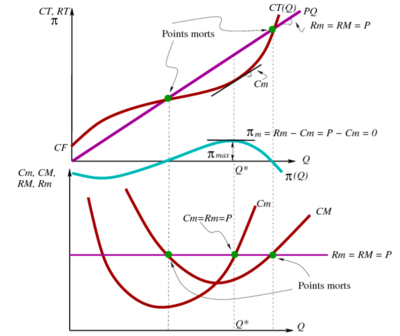
On observe tout d'abord les courbes de coût total (<math>CT</math>), de recette totale (<math>RT</math>), et de profit (<math>\pi</math>) en fonction de la quantité (<math>Q</math>). La courbe de coût total commence au-dessus de l'origine, au niveau des coûts fixes (<math>CF</math>), et augmente avec la quantité produite. La courbe de recette totale débute à l'origine et s'élève également, mais à un taux constant, reflétant un prix de vente (<math>P</math>) constant par unité vendue. | |||
La différence entre les recettes totales et les coûts totaux à chaque niveau de production génère la courbe de profit, qui atteint son maximum (<math>\pi_{max}</math>) au point où la quantité produite est <math>Q^*</math>. Ce point représente la quantité qui maximise le profit total de l'entreprise. La maximisation du profit se produit lorsque la pente de la courbe de recette totale (la recette marginale, <math>Rm</math>) est égale à la pente de la courbe de coût total (le coût marginal, <math>Cm</math>). Graphiquement, c'est là où les deux courbes se croisent. | |||
En dessous de cette intersection, le profit marginal est positif, ce qui signifie que produire une unité supplémentaire augmente le profit total. Au-delà de ce point, le profit marginal devient négatif, ce qui indique que produire des unités supplémentaires réduit le profit total. C'est également le point où le coût marginal devient supérieur au prix et donc à la recette marginale, ce qui explique pourquoi la production supplémentaire n'est pas profitable. | |||
Les "points morts" indiqués sur le graphique correspondent aux niveaux de production où le profit est nul. Ces points sont situés là où la courbe de coût total coupe la courbe de recette totale. Entre ces deux points, l'entreprise réalise un profit; en dehors de ces points, l'entreprise subit des pertes. | |||
La courbe de coût moyen (<math>CM</math>) atteint un minimum avant d'augmenter, ce qui reflète les économies d'échelle suivies des déséconomies d'échelle. Le point où la courbe de coût moyen coupe la ligne de prix est le point où le profit moyen est maximisé. Cependant, ce n'est pas le but principal de l'entreprise, qui cherche à maximiser le profit total, pas le profit moyen. | |||
Le graphique montre ainsi l'importance cruciale de la prise de décision basée sur les coûts et recettes marginaux plutôt que moyens. Il illustre la manière dont la prise en compte des coûts marginaux, en particulier, guide l'entreprise vers le niveau de production optimal qui maximise le profit total. Cela souligne également la nature dynamique des coûts dans la production et la manière dont l'analyse marginale permet d'optimiser la performance financière d'une entreprise. | |||
== Profit == | == Profit == | ||
Le profit maximum est | Le profit maximum d'une entreprise est atteint lorsque la différence entre la recette totale (RT) et le coût total (CT) est la plus grande. Ce point est identifié par la quantité <math>q^*</math>, où les décisions marginales de production rencontrent l'équilibre parfait entre coûts additionnels et revenus additionnels. | ||
<math>\pi = RT - CT = RM \times q | Le profit (<math>\pi</math>) peut être exprimé de différentes manières, mais fondamentalement, il est la différence entre la recette totale et le coût total à la quantité qui maximise le profit, soit <math>\pi = RT - CT</math>. La recette totale est le produit du prix de vente par unité (p), qui est également la recette moyenne (RM) dans un marché concurrentiel, et la quantité vendue (<math>q</math>), d'où <math>RT = RM \times q</math>. Le coût total peut être décomposé en coût moyen (CM) multiplié par la quantité, soit <math>CT = CM \times q</math>. | ||
En soustrayant le coût total de la recette totale, le profit peut aussi être formulé en termes de recette et de coût par unité, ce qui donne <math>\pi = (RM \times q) - (CM \times q)</math>. Comme le prix de vente par unité est égal à la recette moyenne dans un marché parfaitement concurrentiel, c'est-à-dire <math>RM = p</math>, et en factorisant par la quantité <math>q</math>, on obtient <math>\pi = (p - CM) \times q</math>. Cette expression montre que le profit est également la différence entre le prix et le coût moyen par unité, multipliée par le nombre d'unités vendues. | |||
Cela indique que pour maximiser les profits, l'entreprise doit non seulement considérer le coût et la recette par unité, mais aussi l'impact de la production sur ces coûts et recettes à la marge. En pratique, cela implique de continuer à produire jusqu'à ce que le coût de production d'une unité supplémentaire (coût marginal) soit égal au revenu généré par la vente de cette unité (recette marginale), ce qui est le fondement de la prise de décision en termes de maximisation du profit. | |||
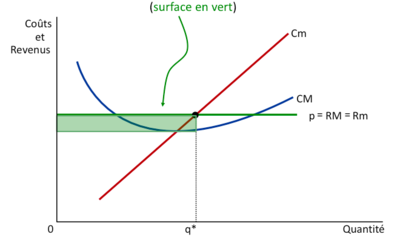
[[Fichier:Marché compétitif profit 1.png|400px|vignette|centré]] | [[Fichier:Marché compétitif profit 1.png|400px|vignette|centré]]Ce graphique illustre un modèle économique classique de maximisation du profit dans un marché concurrentiel. Il montre les relations entre le coût marginal (Cm), le coût moyen (CM), la recette moyenne (RM), qui est également égale à la recette marginale (Rm) et au prix de vente (p), en fonction de la quantité produite (Q). | ||
La ligne horizontale représente le prix de vente (p) par unité, qui, dans un marché parfaitement concurrentiel, est égal à la recette moyenne (RM) ainsi qu'à la recette marginale (Rm). Cette horizontalité indique que le prix est constant quel que soit le niveau de production ; il est déterminé par le marché et est le même pour toutes les unités vendues. | |||
La courbe de coût moyen (CM) descend, atteint un minimum, puis remonte, ce qui reflète généralement les économies d'échelle réalisées jusqu'à un certain point, après lequel les déséconomies d'échelle commencent à se manifester. La courbe de coût marginal (Cm) croise la courbe de coût moyen (CM) à son point le plus bas, ce qui est typique dans la théorie économique car le coût marginal coupe le coût moyen à son minimum. | |||
Le point où la courbe de coût marginal (Cm) croise la ligne du prix de vente (p), noté q*, est le niveau de production qui maximise le profit de l'entreprise. À cette quantité, le coût supplémentaire de production d'une unité supplémentaire est exactement égal au revenu supplémentaire généré par sa vente. Produire plus que q∗ entraînerait des coûts supplémentaires supérieurs aux revenus générés par la vente des unités supplémentaires, diminuant ainsi le profit total. | |||
La surface en vert représente le profit total, qui est la zone entre la courbe des recettes totales et la courbe des coûts totaux. Ce profit est maximisé à la quantité q*, où la différence entre les recettes totales et les coûts totaux est la plus grande. | |||
Ce graphique montre clairement l'importance de la prise de décision basée sur les coûts et recettes marginaux pour la maximisation du profit dans un marché concurrentiel. Il illustre comment les coûts moyens et marginaux évoluent avec la production et comment ces coûts doivent être pris en compte par les entreprises pour déterminer le niveau de production optimal. | |||
== Maximisation du π : un exemple analytique == | |||
<math>Cm = 10 - 2q + q^2 = 13 | Pour déterminer la quantité qui maximise le profit de l'entreprise lorsque le prix de marché est <math>p = 13</math>, nous devons nous référer à la condition de premier ordre (CPO) où le coût marginal (<math>Cm</math>) est égal au prix de marché. La fonction de coût est donnée par <math>CT = 1 + 10q - q^2 + \frac{1}{3}q^3</math>. La dérivée de cette fonction par rapport à <math>q</math> donnera le coût marginal (<math>Cm</math>), qui est égal à <math>10 - 2q + q^2</math>. En égalisant le coût marginal au prix, nous avons <math>10 - 2q + q^2 = 13</math>. | ||
Pour résoudre cette équation quadratique, nous | Pour résoudre cette équation quadratique, nous appliquons la formule quadratique : <math>q = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}</math>. Cela nous donne <math>q = \frac{2 \pm \sqrt{4 - 4(1)(-3)}}{2} = \frac{2 \pm \sqrt{16}}{2}</math>. Les solutions de cette équation sont <math>q = \frac{6}{2}</math> et <math>q = \frac{-2}{2}</math>. | ||
<math>q | Cependant, nous excluons la solution négative car une quantité produite ne peut pas être négative, laissant <math>q = 3</math> comme la quantité qui maximise le profit de l'entreprise. | ||
= Offre de la firme de court et de long terme = | |||
== La courbe d’offre de l’entreprise à court terme == | == La courbe d’offre de l’entreprise à court terme == | ||
La courbe d'offre à court terme d'une entreprise dans un marché compétitif coïncide avec sa courbe de coût marginal au-dessus du point de fermeture, c'est-à-dire là où le coût marginal est supérieur au coût moyen variable. La raison en est qu'à court terme, l'entreprise doit couvrir au moins ses coûts variables pour continuer à fonctionner. Si le prix de marché est inférieur au coût variable moyen, l'entreprise choisira de ne pas produire et de minimiser ses pertes en couvrant seulement ses coûts fixes, qui sont inévitables à court terme. | |||
La courbe de coût marginal est dérivée de la fonction de coût total et montre le coût additionnel de production d'une unité supplémentaire. À court terme, tant que le prix de marché est supérieur au coût marginal, l'entreprise continuera d'augmenter sa production car chaque unité supplémentaire vendue contribuera à couvrir les coûts fixes et à générer un profit. Lorsque le coût marginal est égal au prix de marché, l'entreprise maximise son profit car la production d'une unité supplémentaire n'apporterait ni profit ni perte supplémentaire. | |||
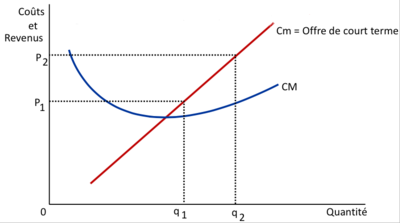
À plus long terme, la courbe d'offre peut différer de la courbe de coût marginal en raison de l'entrée de nouvelles entreprises sur le marché ou de la sortie d'entreprises existantes, ce qui affecte les coûts totaux et variables, ainsi que la capacité de production globale. De plus, à long terme, les coûts fixes peuvent devenir variables, permettant à l'entreprise d'ajuster tous ses coûts en réponse aux changements du marché.[[Fichier:Courbe d’offre de l’entreprise à court terme 1.png|400px|vignette|centré]]Le graphique montre les courbes de coût marginal (Cm) et de coût moyen (CM) d'une entreprise par rapport à la quantité produite. La courbe de coût marginal, qui est également étiquetée comme l'offre de court terme, est ascendante, indiquant que le coût de production d'une unité supplémentaire augmente avec la quantité produite. Ceci est conforme à la loi des rendements décroissants, où l'ajout de facteurs de production supplémentaires à un certain point entraîne une diminution du rendement marginal. | |||
La courbe de coût moyen a une forme en U, suggérant que l'entreprise expérimente initialement des économies d'échelle à mesure que la production augmente (le coût moyen diminue), mais après avoir atteint un certain niveau de production (pas nécessairement montré dans ce graphique), les déséconomies d'échelle entraîneront une augmentation du coût moyen. | |||
Deux prix de marché différents sont représentés, P1 et P2, avec P2 étant supérieur à P1. Ces prix coupent la courbe de coût marginal à deux points différents, définissant les quantités q1 et q2, respectivement, que l'entreprise est disposée à offrir à ces prix dans le cadre d'un marché compétitif. À P1, la quantité offerte est q1, tandis qu'à P2, la quantité offerte est q2. Cela démontre que l'offre de l'entreprise est directement liée au coût marginal de production. | |||
Il est important de noter que l'offre de court terme de l'entreprise est représentée par la portion de la courbe de coût marginal qui se situe au-dessus de la courbe de coût moyen. Cela indique que l'entreprise ne fournira pas de biens sur le marché à un prix qui ne couvre pas au moins le coût moyen, car cela signifierait opérer à perte. | |||
Le graphique illustre clairement que l'entreprise ajustera sa quantité offerte en réponse aux changements de prix du marché pour maximiser son profit. Lorsque le prix du marché augmente de P1 à P2, il devient rentable pour l'entreprise d'augmenter sa production de q1 à q2, car le prix de marché couvre le coût marginal de production des unités supplémentaires. | |||
== Décision de fermeture à court terme == | |||
La | La décision de fermeture à court terme pour une entreprise fait référence à la situation où l'entreprise doit décider si elle continue d'opérer ou si elle cesse ses activités en raison de pertes financières. À court terme, les coûts fixes (tels que le loyer, l'équipement et les salaires des employés permanents) ne peuvent pas être ajustés car ils sont engagés indépendamment de la production. Cela signifie que, même si l'entreprise cesse de produire, ces coûts fixes doivent toujours être payés. | ||
Le coût variable moyen (CVM) représente le coût moyen des variables de production par unité de bien ou de service produite. Dans un contexte de court terme, si le prix du marché est inférieur au coût variable moyen, l'entreprise subit une perte sur chaque unité produite. Dans ce cas, il serait plus judicieux pour l'entreprise de cesser la production, car la perte résultant de la production serait plus grande que les coûts fixes seuls. En d'autres termes, il est préférable pour l'entreprise de subir une perte égale aux coûts fixes plutôt que de subir des pertes encore plus importantes en couvrant également les coûts variables. | |||
La règle générale est que si le prix de marché est supérieur au coût variable moyen, l'entreprise devrait continuer à produire à court terme, même si elle subit des pertes totales, car en produisant, elle peut couvrir une partie de ses coûts fixes et réduire la perte globale. Si le prix est inférieur au coût variable moyen, l'entreprise devrait envisager de fermer temporairement car chaque unité produite augmente la perte totale. | |||
La décision de continuer à opérer ou de fermer temporairement est donc fortement influencée par la relation entre le prix de marché et le coût variable moyen à court terme. | |||
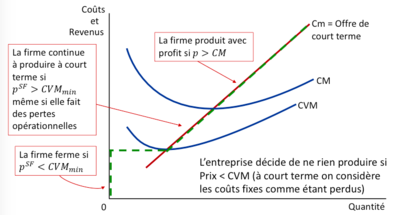
[[Fichier:Décision de fermeture à court terme 1.png|400px|vignette|centré]] | |||
<math> | Le graphique illustre la prise de décision d'une entreprise concernant la production à court terme en fonction des coûts et du prix de vente. Il montre trois courbes : la courbe de coût marginal (<math>Cm</math>), qui représente également l'offre de court terme de l'entreprise, la courbe de coût moyen (<math>CM</math>), et la courbe de coût variable moyen (<math>CVM</math>). | ||
Selon le graphique, il y a trois décisions possibles pour l'entreprise en fonction du prix de marché (noté ici comme <math>p^{SF}</math>, le prix de vente à court terme) : | |||
#Si <math>p^{SF}</math> est supérieur au coût moyen (<math>CM</math>) : L'entreprise produit et réalise un profit, car le prix de vente couvre à la fois les coûts variables et fixes par unité produite. | |||
#Si <math>p^{SF}</math> est inférieur au coût variable moyen minimum (<math>CVM_{\text{min}}</math>) : L'entreprise décide de ne rien produire et de fermer temporairement car le prix de vente ne couvre même pas les coûts variables. À court terme, les coûts fixes sont considérés comme perdus car ils ne dépendent pas de la décision de produire. | |||
#Si <math>p^{SF}</math> est supérieur au <math>CVM_{\text{min}}</math> mais inférieur au <math>CM</math> : L'entreprise continue à produire à court terme malgré des pertes opérationnelles, car le prix de vente couvre les coûts variables et contribue partiellement aux coûts fixes. Il s'agit d'une situation où la production permet de minimiser les pertes en comparaison avec une fermeture complète. | |||
La courbe de <math>CVM</math> montre la baisse des coûts variables unitaires avec l'augmentation de la production jusqu'à un certain point, après quoi les coûts variables par unité commencent à augmenter en raison des déséconomies d'échelle. | |||
L'intersection de la courbe de <math>Cm</math> avec la courbe de <math>CM</math> détermine le seuil de rentabilité à long terme, où l'entreprise couvre tous ses coûts et commence à réaliser des profits si le prix de marché est égal ou supérieur à ce niveau. En dessous de ce seuil, l'entreprise peut continuer à fonctionner à court terme tant que le prix de marché reste supérieur au <math>CVM</math>. | |||
Le graphique souligne l'importance de la distinction entre les décisions à court et à long terme. À court terme, les coûts fixes sont irrécupérables et l'entreprise vise à couvrir ses coûts variables tout en contribuant au maximum aux coûts fixes. À long terme, tous les coûts deviennent variables, et l'entreprise devra considérer la rentabilité globale pour sa survie et sa décision de rester sur le marché. | |||
L'entreprise fait face à un choix crucial en période de conditions de marché défavorables : continuer à produire ou arrêter la production. La décision dépend de la comparaison entre les profits (ou les pertes réduites) réalisés en produisant par rapport à ceux en cessant toute production. | |||
Si l'entreprise ne produit pas, la quantité produite est nulle (<math>q = 0</math>), et le profit (ou plutôt la perte, car les coûts fixes doivent toujours être payés même si rien n'est produit) est simplement le négatif des coûts fixes (<math>\pi(0) = -CF</math>). En revanche, si l'entreprise produit une quantité positive <math>q = q^*</math>, le profit est la différence entre la recette totale (le prix de marché multiplié par la quantité produite) et la somme des coûts variables et des coûts fixes (<math>\pi(q^*) = pq^* - CV(q^*) - CF</math>). | |||
L'entreprise choisira de produire une quantité positive si le profit de produire <math>q^*</math> est supérieur au profit de ne rien produire, c'est-à-dire si <math>\pi(q^*) > \pi(0)</math>. Cela se traduit par la condition où le revenu total de la production dépasse les coûts variables (<math>pq^* > CV(q^)</math>), ou, en d'autres termes, si le prix de marché est supérieur au coût variable moyen à la quantité <math>q^*</math> (<math>p > CVM(q^*)</math>). | |||
En | En période de difficultés, l'entreprise pourrait donc continuer à produire tant que le prix de marché est supérieur au coût variable moyen minimum (<math>CVM_{min}</math>), définissant ainsi le seuil de fermeture. Ce seuil est le niveau de prix minimum nécessaire pour que l'entreprise couvre ses coûts variables. Si le prix du marché est inférieur à ce seuil, il serait plus rationnel pour l'entreprise de cesser la production pour minimiser ses pertes, car même les coûts variables ne seraient pas couverts. | ||
En résumé, l'entreprise | En résumé, l'entreprise continue à produire au-dessus du seuil de fermeture pour réduire ses pertes, même si elle opère à perte, car elle contribue au moins partiellement à la couverture des coûts fixes, ce qui est préférable à ne pas produire du tout et à payer l'intégralité des coûts fixes sans aucun revenu pour compenser. | ||
[[Fichier:Décision de fermeture à court terme 2.png|400px|vignette|centré]] | |||
Le graphique présente la relation entre les coûts d'une entreprise et le prix de marché, illustrant la prise de décision en termes de production et de fermeture à court terme. Il montre les courbes de coût marginal (Cm), de coût moyen (CM) et de coût variable moyen (CVM), ainsi que le seuil de fermeture. | |||
La courbe de coût marginal (Cm) est ascendante, indiquant que le coût de production d'une unité supplémentaire augmente avec chaque unité produite. La courbe de coût moyen (CM) a une forme en U typique, indiquant des économies d'échelle jusqu'à un certain point (le minimum de la courbe CM), après quoi les coûts moyens commencent à augmenter à cause des déséconomies d'échelle. | |||
Trois prix de marché différents sont indiqués : P2, P1 et le seuil de fermeture (PsF). | |||
*À P2, le profit est positif (<math>\pi > 0</math>) car le prix de marché est supérieur au coût moyen et au coût marginal, ce qui signifie que l'entreprise couvre tous ses coûts et réalise un bénéfice. | |||
*À P1, l'entreprise subit des pertes d'exploitation (<math>-CF < \pi < 0</math>) car le prix de marché couvre les coûts variables mais pas la totalité des coûts fixes. Toutefois, tant que le prix est au-dessus du seuil de fermeture, il est plus avantageux pour l'entreprise de continuer à produire à court terme plutôt que de fermer complètement, car les recettes générées contribuent aux coûts fixes. | |||
*Le seuil de fermeture (PsF) est le prix de marché auquel le profit est égal à la perte totale des coûts fixes (<math>-CF = \pi < 0</math>). Si le prix du marché tombe en dessous de ce seuil, les recettes de l'entreprise ne couvrent même pas les coûts variables, et il est donc préférable pour l'entreprise de cesser la production pour minimiser les pertes. | |||
La "Courbe d’offre individuelle à court terme" est la partie de la courbe de coût marginal au-dessus de la courbe de coût variable moyen, indiquant la quantité que l'entreprise est disposée à fournir à différents prix. Si le prix tombe en dessous du seuil de fermeture, l'entreprise a intérêt à cesser son activité, car même les coûts variables ne seraient pas couverts, ce qui mènerait à des pertes supérieures aux coûts fixes seuls. | |||
En résumé, ce graphique démontre comment l'entreprise ajuste sa production en fonction du prix de marché et de ses coûts. Il souligne l'importance du seuil de fermeture comme point de décision critique pour continuer la production à court terme malgré les pertes opérationnelles, avec l'objectif de couvrir au moins les coûts variables et de contribuer aux coûts fixes. | |||
== La courbe d’offre de l’entreprise à long terme == | == La courbe d’offre de l’entreprise à long terme == | ||
En économie, l'offre d'une entreprise à long terme est représentée différemment de celle à court terme en raison de la flexibilité qu'a l'entreprise pour ajuster tous ses coûts. À long terme, il n'y a pas de coûts fixes; tous les coûts sont variables, car l'entreprise a suffisamment de temps pour ajuster sa taille et sa capacité de production. Cela signifie que l'entreprise peut entrer ou sortir du marché et ajuster son niveau de production sans être contrainte par des coûts irrécupérables. | |||
La courbe de coût marginal à long terme (CmLT) reflète le coût additionnel de production d'une unité supplémentaire en considérant que l'entreprise peut varier tous ses facteurs de production. La courbe de coût moyen à long terme (CMLT) représente le coût par unité si l'entreprise ajuste sa taille de manière optimale pour chaque niveau de production. | |||
La courbe d'offre de l'entreprise à long terme | La portion de la courbe de coût marginal de long terme qui se situe au-dessus de la courbe de coût moyen à long terme correspond à la courbe d'offre de l'entreprise à long terme. Cela est dû au fait que, pour maximiser le profit, l'entreprise ne produira et n'offrira des unités supplémentaires sur le marché que si le coût marginal de production de ces unités est inférieur ou égal au prix. Si le coût marginal est supérieur au coût moyen, cela signifie que produire une unité supplémentaire augmenterait le coût moyen, indiquant que l'entreprise n'est pas dans une situation optimale de production. | ||
Ainsi, si le prix de marché est supérieur au coût moyen à long terme, l'entreprise trouvera profitable d'augmenter sa production, car chaque unité supplémentaire vendue apportera un revenu supérieur au coût moyen de production. En revanche, si le prix est inférieur au coût moyen, l'entreprise réduira sa production ou quittera le marché, car elle ne pourrait pas couvrir ses coûts à long terme. | |||
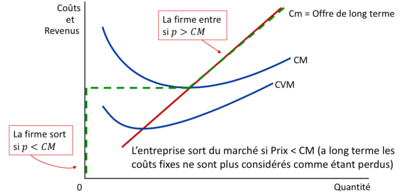
L'offre à long terme d'une entreprise dans un marché parfaitement concurrentiel est donc représentée par la partie ascendante de sa courbe de coût marginal de long terme, à partir du point où elle coupe la courbe de coût moyen de long terme. Cela reflète la capacité et la volonté de l'entreprise de fournir des quantités supplémentaires au marché à un prix qui couvre tous les coûts, incluant un retour sur l'investissement.[[Fichier:Courbe d’offre de l’entreprise à long terme 1.png|400px|vignette|centré]]Ce graphique dépeint un scénario économique qui décrit les conditions sous lesquelles une entreprise décide de rester active sur le marché ou de s'en retirer à long terme. Il représente les coûts moyens et marginaux de l'entreprise ainsi que les différents prix de marché et leurs implications pour les décisions de l'entreprise. | |||
Nous voyons trois courbes distinctes sur le graphique. La courbe de coût variable moyen (CVM) représente le coût moyen de production excluant les coûts fixes, et elle est la plus basse des trois. La courbe de coût moyen (CM) montre le coût moyen total par unité, y compris les coûts fixes et variables. Cette courbe a une forme en U, suggérant que l'entreprise bénéficie d'économies d'échelle jusqu'à un certain point avant que les déséconomies d'échelle ne prennent effet. La courbe de coût marginal (Cm) indique le coût supplémentaire de production d'une unité supplémentaire et, à long terme, cette courbe est synonyme de l'offre de l'entreprise, mais seulement pour la portion qui se situe au-dessus de la courbe de CM. | |||
La décision de l'entreprise d'entrer ou de sortir du marché dépend du prix de marché par rapport à ces coûts. Lorsque le prix de marché dépasse le coût moyen (comme indiqué par P2 sur le graphique), l'entreprise réalise un profit, car elle est en mesure de couvrir tous ses coûts par unité produite et de générer des revenus supplémentaires. Dans ce cas, l'entreprise a une incitation claire à rester sur le marché. | |||
Si le prix de marché est en dessous du coût moyen mais au-dessus du CVM, comme illustré par P1, l'entreprise opère à perte, car bien qu'elle couvre ses coûts variables, elle ne peut pas couvrir la totalité de ses coûts fixes. Toutefois, si elle anticipe une amélioration future des prix, elle peut décider de rester en activité à court terme, subissant des pertes opérationnelles dans l'espoir de jours meilleurs. | |||
Le seuil de fermeture est le niveau de prix de marché où l'entreprise couvre tout juste ses coûts variables, illustré par la ligne horizontale étiquetée PsF. Si les prix tombent en dessous de ce seuil, la firme décide de quitter le marché car les recettes de vente ne suffiraient même pas à couvrir les coûts variables de production, sans parler des coûts fixes. À ce point, toute production supplémentaire aggraverait les pertes financières de l'entreprise. | |||
Ce graphique illustre l'importance pour les entreprises de surveiller attentivement le marché et de comprendre leur structure de coûts. Les décisions à long terme doivent être prises avec une compréhension claire du point d'équilibre et du seuil de rentabilité pour garantir la viabilité et la durabilité de l'entreprise dans un environnement de marché concurrentiel. | |||
== Décision de sortir/entrer == | |||
La différence entre fermeture et sortie est une distinction cruciale dans la théorie économique, liée aux horizons temporels et à la récupérabilité des coûts. La fermeture est une décision à court terme où l'entreprise cesse la production pour une période donnée, souvent en réponse à des conditions de marché défavorables. Durant cette période, l'entreprise ne génère aucun revenu d'exploitation, mais elle doit toujours faire face à ses coûts fixes (CF), qui sont des coûts irrécouvrables dans le sens où ils ne peuvent pas être récupérés une fois qu'ils ont été payés. Par exemple, les dépenses en capital sur des machines ou des installations, qui ne peuvent pas être vendues ou utilisées pour d'autres fins sans perte significative, sont considérées comme des coûts fixes. | |||
' | D'autre part, la sortie du marché est une décision à long terme. Elle est prise lorsque l'entreprise prévoit que les conditions de marché ne vont pas s'améliorer suffisamment pour couvrir ses coûts à l'avenir. Dans ce cas, l'entreprise prend en compte tous les coûts, y compris les coûts fixes irrécouvrables, pour décider de cesser définitivement ses opérations. La sortie implique souvent des mesures telles que la vente d'actifs, le licenciement du personnel et la fermeture de sites de production, avec l'intention de ne pas revenir sur le marché. | ||
Si | L'ignorance des coûts fixes lors de la prise de décision de fermeture temporaire est justifiée par le fait que ces coûts seront encourus que l'entreprise produise ou non. Par conséquent, la décision de produire ou de fermer temporairement se base plutôt sur les coûts variables et la capacité de l'entreprise à couvrir ces coûts avec le revenu généré par les ventes. Si le prix de marché ne couvre pas au moins les coûts variables moyens, il est préférable pour l'entreprise de fermer temporairement. | ||
La décision de fermeture temporaire est donc guidée par la viabilité à court terme et la comparaison des revenus avec les coûts variables, tandis que la décision de sortie du marché est une considération à long terme qui prend en compte la totalité des coûts de l'entreprise et les perspectives à long terme de rentabilité sur le marché. | |||
<math> | Si une entreprise constate que la recette totale qu'elle obtiendrait de sa production est inférieure à ses coûts totaux à long terme, elle choisira de quitter le marché. Cela est exprimé mathématiquement comme <math>RT < CT</math>. En termes de coûts et de recettes par unité, cette condition peut être reformulée pour indiquer que si le prix de marché (<math>p</math>) est inférieur au coût moyen (<math>CM</math>), l'entreprise subira des pertes et ne pourra pas couvrir ses coûts totaux, ce qui justifie la sortie du marché : <math>p < CM</math>. | ||
Inversement, si l'entreprise anticipe que la recette totale de sa production dépasserait ses coûts totaux, elle réalisera un profit et sera incitée à entrer sur le marché ou à y rester si elle y est déjà. Mathématiquement, cela signifie que si <math>RT > CT</math>, ou à l'unité, que si le prix (<math>p</math>) est supérieur au coût moyen (<math>CM</math>), alors l'entreprise peut opérer de manière rentable : <math>p > CM</math>. | |||
La courbe d'offre à long terme de l'entreprise reflète la portion de sa courbe de coût marginal qui se trouve au-dessus du coût moyen total. Cela est dû au fait que, à long terme, les entreprises ne resteront sur le marché que si elles peuvent produire à un coût qui leur permet de réaliser un profit, c'est-à-dire lorsque le coût marginal de production d'une unité supplémentaire est égal ou inférieur au prix que l'entreprise peut obtenir sur le marché. À long terme, les entreprises ajustent leur taille et leur capacité de production pour minimiser les coûts et maximiser les profits, ce qui entraîne une offre de marché basée sur le coût marginal par rapport au coût moyen total. | |||
= Offre agrégée = | |||
== La courbe d’offre agrégée à court terme == | |||
La courbe d'offre agrégée sur un marché est créée par l'agrégation des courbes d'offre de toutes les entreprises individuelles qui opèrent sur ce marché. Cette agrégation est faite de manière horizontale, ce qui signifie que pour chaque niveau de prix donné, les quantités offertes par toutes les entreprises sont additionnées pour obtenir la quantité totale offerte sur le marché à ce prix. | |||
Pour clarifier, si nous avons deux entreprises, A et B, et que pour un prix P, l'entreprise A est prête à vendre 10 unités de son produit et l'entreprise B est prête à vendre 15 unités, alors l'offre agrégée à ce prix serait de 25 unités. Si nous traçons ces quantités offertes contre le prix pour toutes les entreprises du marché, nous obtenons la courbe d'offre agrégée. | |||
Cette courbe reflète donc non seulement la réponse de l'offre des entreprises individuelles aux changements de prix, mais aussi l'entrée et la sortie des entreprises du marché, qui peut varier en fonction des conditions économiques et des barrières à l'entrée ou à la sortie. À court terme, l'offre agrégée peut être relativement inélastique, car les entreprises ont des capacités de production et des coûts fixes qui ne peuvent pas être rapidement ajustés. À long terme, cependant, l'offre agrégée peut devenir plus élastique car les entreprises ont le temps d'ajuster leur production et de nouvelles entreprises peuvent entrer sur le marché, augmentant ainsi la quantité totale offerte à chaque niveau de prix. | |||
Avec un nombre fixe d’entreprises (sans sortie ou entrée d’entreprises dans le marché), c’est-à-dire à court terme , on a que : | |||
[[Fichier:Courbe d’offre agrégée à court terme ECP1.png|400px|vignette|centré]] | |||
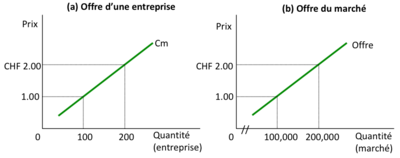
Dans ces deux graphiques, nous observons la représentation de la courbe d'offre d'une entreprise individuelle et de la courbe d'offre agrégée du marché. | |||
Dans les deux graphiques, nous observons la représentation de la courbe d'offre d'une entreprise individuelle et de la courbe d'offre agrégée du marché. | |||
Le graphique (a) montre la courbe d'offre d'une seule entreprise. La ligne verticale représente le coût marginal (Cm) de production, qui augmente linéairement avec la quantité produite. Cette relation linéaire suggère que chaque unité supplémentaire coûte plus cher à produire que la précédente, ce qui est caractéristique d'une situation où il y a des rendements décroissants à la production. La courbe commence au-dessus de zéro, ce qui indique un coût fixe initial avant la production de toute unité. Le prix auquel l'entreprise est prête à offrir chaque quantité supplémentaire sur le marché est représenté par la hauteur de la courbe de coût marginal. | |||
Le graphique (b) illustre la courbe d'offre agrégée du marché, qui est dérivée de l'addition des quantités fournies par chaque entreprise individuelle à chaque niveau de prix. Cette courbe montre également une relation linéaire entre le prix et la quantité offerte, mais à une échelle beaucoup plus grande. La quantité sur l'axe horizontal est considérablement plus élevée, reflétant l'offre totale de toutes les entreprises sur le marché. | |||
Si nous supposons un nombre fixe d'entreprises sur le marché, c'est-à-dire qu'il n'y a pas d'entrée ou de sortie d'entreprises à court terme, la courbe d'offre du marché n'évoluera pas avec le temps. À court terme, les entreprises ne peuvent ajuster que leur production en réponse aux changements de prix, mais elles ne peuvent pas entrer ou sortir du marché assez rapidement pour affecter la courbe d'offre agrégée. Cela implique que la courbe d'offre agrégée est la somme horizontale des courbes d'offre de toutes les entreprises existantes sur le marché. | |||
Ainsi, à court terme, la courbe d'offre du marché représente la réaction totale de toutes les entreprises existantes aux changements de prix, et elle ne changera que si le prix change ou si les coûts de production des entreprises existantes changent. Toute augmentation du nombre d'entreprises ou changements dans la technologie de production, qui pourraient affecter les coûts marginaux, ne seront reflétés dans la courbe d'offre qu'à long terme. | |||
== La courbe d’offre agrégée à long terme == | |||
Dans un marché concurrentiel à long terme, les entreprises ajustent leur niveau de production et les nouvelles entreprises décident d'entrer ou de sortir du marché en fonction des profits économiques réalisés. Ces ajustements sont influencés par la relation entre le prix du marché (P) et le coût moyen (CM) des entreprises. | |||
Si le prix du marché est supérieur au coût moyen, cela indique que les entreprises présentes sur le marché réalisent des profits économiques positifs. Cette situation est attractive pour les nouvelles entreprises, qui choisiront d'entrer sur le marché pour bénéficier de ces profits. L'entrée de nouvelles entreprises accroît la quantité offerte sur le marché, ce qui, selon les lois de l'offre et de la demande, conduit à une baisse du prix du marché. La courbe d'offre agrégée se déplace alors vers la droite. Ce processus se poursuit jusqu'à ce que le prix du marché soit égal au coût moyen, ce qui élimine les profits économiques et rétablit un équilibre. | |||
Inversement, si le prix du marché est inférieur au coût moyen, les entreprises existantes subissent des pertes, ce qui signifie qu'elles font des profits économiques négatifs. Dans cette situation, certaines entreprises choisiront de sortir du marché, ce qui réduit l'offre totale. La diminution de l'offre entraîne une hausse du prix du marché jusqu'à ce qu'il atteigne le niveau du coût moyen. | |||
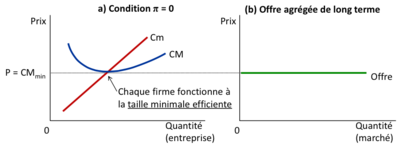
À l'équilibre de long terme, le prix du marché sera égal au coût moyen, et donc, les profits économiques seront nuls. À ce point, il n'y a ni incitation à l'entrée ni à la sortie du marché pour les entreprises, et la courbe d'offre agrégée devient parfaitement élastique ou horizontale. Cela signifie que les entreprises peuvent vendre n'importe quelle quantité de leur produit au prix du marché sans influencer ce prix. Cet équilibre est caractéristique d'une concurrence parfaite où le libre jeu du marché conduit à une efficacité allocative, avec les entreprises produisant à leur niveau le plus efficient. | |||
[[Fichier:Coucourbe d’offre agrégée à long terme 1.png|400px|vignette|centré]] | |||
Le raisonnement à la marge reste fondamental dans la détermination de la production optimale pour une entreprise individuelle, car il indique que l'équilibre de maximisation des profits est atteint lorsque le prix du marché (<math>p</math>) est égal au coût marginal (<math>Cm</math>). Cette condition s'applique à chaque entreprise et dicte la quantité qu'elle offre sur le marché pour maximiser ses profits. | |||
Dans un marché concurrentiel à long terme, cependant, la dynamique change. Si des entreprises réalisent des profits économiques positifs (<math>p > CM</math>), cela attire de nouvelles entreprises sur le marché, augmentant l'offre totale et poussant les prix vers le bas jusqu'à atteindre le niveau du coût moyen (<math>p = CM</math>). Inversement, si des entreprises subissent des pertes (<math>p < CM</math>), certaines quitteront le marché, réduisant l'offre et faisant augmenter les prix jusqu'à ce qu'ils égalisent à nouveau le coût moyen. Ce processus d'entrée et de sortie se poursuit jusqu'à ce que les profits économiques soient nuls, menant à une situation où <math>p = CM</math> et <math>p = Cm</math>. | |||
À ce stade d'équilibre à long terme, les entreprises opèrent là où le coût moyen et le coût marginal sont minimaux et égaux au prix du marché. Cela correspond à la production au point d'efficacité productive minimale ou à l'efficience des échelles minimales (EME), où <math>CM</math> est au plus bas. La courbe d'offre agrégée à long terme est alors horizontale ou parfaitement élastique à ce niveau de prix, indiquant que le marché peut absorber n'importe quelle quantité au prix où les coûts moyens sont minimisés. Aucune entreprise n'a la capacité ou l'incitation à modifier ce prix, car toutes font un profit nul et n'ont donc pas de profits économiques à maximiser. En résumé, le marché à long terme s'ajuste de sorte que <math>p = CM</math> et <math>p = Cm</math>, et la courbe d'offre du marché est parfaitement horizontale au prix correspondant à l'EME. | |||
== Profits économiques nuls : intuition == | |||
Il est essentiel de distinguer entre profit économique et profit comptable, notamment lorsqu'on analyse les conditions d'équilibre d'une entreprise sur le marché à long terme. Un profit économique nul ne signifie pas que les propriétaires d'une entreprise ne tirent aucun revenu de leur investissement. En réalité, cela indique que l'entreprise génère juste assez de revenus pour couvrir tous ses coûts, y compris les coûts d'opportunité associés à l'investissement de capital et au temps des propriétaires. | |||
Le coût d'opportunité est la valeur de la meilleure alternative à laquelle on renonce lorsqu'on fait un choix. Dans le contexte d'une entreprise, cela inclut les revenus que les propriétaires pourraient obtenir s'ils investissaient leur temps et leur argent ailleurs. Ainsi, à l'équilibre de profit nul, l'entreprise compense ses propriétaires pour ces coûts d'opportunité, ce qui signifie qu'ils reçoivent le retour qu'ils auraient pu espérer de leur second meilleur investissement ou emploi de leur temps et de leur argent. | |||
En termes comptables, les profits peuvent apparaître comme positifs. Cela est dû au fait que le profit comptable est calculé en soustrayant les coûts explicites des revenus totaux, sans prendre en compte les coûts implicites ou d'opportunité. Par conséquent, une entreprise peut afficher un profit comptable tout en ayant un profit économique nul. Le profit économique est une mesure plus complète de la rentabilité, car il inclut à la fois les coûts explicites et implicites. | |||
Dans un marché parfaitement concurrentiel à long terme, les profits économiques nuls sont la norme, car les forces du marché érodent les profits économiques positifs par l'entrée de nouvelles entreprises, et les profits économiques négatifs par la sortie des entreprises existantes. Ce processus se poursuit jusqu'à ce que toutes les entreprises sur le marché ne réalisent plus que des profits économiques nuls, assurant ainsi que les ressources sont allouées de la manière la plus efficace possible, c'est-à-dire là où elles sont les plus valorisées. | |||
== | == Courbe d’offre de long terme croissante == | ||
La courbe d'offre à long terme peut présenter une pente positive dans certaines situations, même dans le cadre de la concurrence parfaite. La pente positive de la courbe d'offre à long terme reflète l'idée que, bien que les entreprises puissent entrer et sortir librement du marché, toutes les entreprises ne sont pas identiques, et les ressources qu'elles utilisent ne sont pas parfaitement substituables et peuvent être limitées. | |||
Un facteur clé de cette dynamique est la disponibilité limitée de certaines ressources ou facteurs de production. Prenons l'exemple de la terre agricole : elle est disponible en quantité limitée et toutes les parcelles de terre ne sont pas également fertiles. Au fur et à mesure que la production agricole s'accroît, les nouvelles entreprises peuvent être forcées d'utiliser des terres moins productives ou plus coûteuses à cultiver, ce qui augmente leur coût moyen de production. | |||
À mesure que de nouvelles entreprises entrent sur le marché en réponse à des profits économiques positifs, elles font face à des coûts plus élevés que les entreprises déjà établies. Cela signifie que même si le prix du marché est suffisant pour couvrir les coûts des entreprises existantes, il ne peut pas être suffisant pour les nouvelles entreprises avec des coûts plus élevés. En conséquence, l'entreprise marginale - celle qui est indifférente entre entrer sur le marché ou non en raison de ses coûts plus élevés - détermine le prix du marché à l'équilibre. | |||
La condition de profit nul s'applique donc à cette entreprise marginale et non à toutes les entreprises du marché. Les entreprises plus établies ou plus efficaces réaliseront des profits économiques, mais l'entrée de nouvelles entreprises avec des coûts plus élevés se poursuivra jusqu'à ce que les prix baissent suffisamment pour éliminer ces profits économiques pour l'entreprise marginale. | |||
La courbe d'offre à long terme avec une pente positive est donc le résultat de l'entrée de nouvelles entreprises avec des fonctions de coût progressivement plus élevées, et elle reste plus élastique que la courbe d'offre à court terme. Cela est dû au fait qu'à court terme, les entreprises ne peuvent pas ajuster leur taille ou leur structure de coûts, et donc l'offre est moins sensible aux changements de prix. À long terme, avec la possibilité d'ajuster la production et l'entrée et la sortie de nouvelles entreprises, la courbe d'offre peut devenir plus réactive aux changements de prix, même si elle présente une pente positive. | |||
== | == Mécanisme d’ajustement : court versus long terme == | ||
=== Situation initiale === | |||
Les deux graphiques suivants illustrent la dynamique de l'offre et de la demande dans une situation initiale à court et à long terme pour une entreprise et pour un marché. | |||
Dans le premier graphique, dédié à une entreprise individuelle, nous voyons deux courbes: la courbe de coût moyen (CM) et la courbe de coût marginal (Cm). La courbe de coût marginal croise la courbe de coût moyen à son point le plus bas, ce qui est typique car cela indique le niveau de production le plus efficace pour l'entreprise. Le prix de marché (P1) est indiqué et il semble être égal au coût marginal et au coût moyen, ce qui signifierait que l'entreprise fait ni profit ni perte; elle couvre juste ses coûts. | |||
Le deuxième graphique montre l'offre et la demande sur le marché global. L'offre à court terme (S1) est représentée par une courbe ascendante, indiquant que plus le prix est élevé, plus les entreprises sont disposées à offrir de produits. La courbe d'offre à long terme est représentée comme une ligne horizontale, ce qui indique que le marché peut absorber toute quantité au prix P1 sans que cela affecte le prix, reflétant une situation d'équilibre à long terme où les entreprises ne font que couvrir leurs coûts. La demande (D1) croise l'offre à court terme au point A, définissant la quantité de marché initiale (q1) et le prix P1. | |||
[[Fichier:Mécanisme d’ajustement court versus long terme 1.png|400px|vignette|centré]]L'analyse des graphiques montre un mécanisme d'ajustement de marché: | |||
# À court terme : Si le prix de marché est au-dessus du coût moyen, les entreprises existantes réaliseront des profits, incitant à une augmentation de l'offre. Si le prix est en dessous du coût moyen, les entreprises subiront des pertes, menant à une réduction de l'offre. La courbe de coût marginal indique la quantité que l'entreprise est prête à fournir à différents prix. | |||
# À long terme : La courbe d'offre à long terme est parfaitement élastique au prix P1, ce qui suggère que le marché est en équilibre et que toutes les entreprises opèrent à un niveau où le coût moyen est égal au prix de marché. À ce stade, aucune nouvelle entreprise n'a d'incitation à entrer sur le marché, et aucune entreprise n'a d'incitation à sortir, car toutes couvrent leurs coûts, y compris un retour normal sur le capital (représenté par le coût moyen). | |||
Le mécanisme d'ajustement entre court et long terme est donc caractérisé par des entrées et sorties d'entreprises du marché jusqu'à ce que le profit économique soit nul, et que le prix se stabilise au niveau où les entreprises couvrent tous leurs coûts, y compris le coût d'opportunité du capital et du travail. Cela entraîne une offre de marché plus élastique à long terme par rapport à court terme, où la quantité produite peut fluctuer plus largement en réponse aux changements de prix sans que cela affecte le prix lui-même. | |||
=== Choc exogène positif de demande === | |||
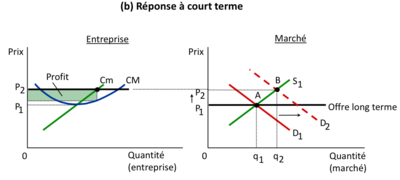
Ces deux graphiques illustrent la réaction à court terme d'une entreprise et d'un marché global à un choc exogène positif de la demande, entraînant une augmentation du prix. | |||
[[Fichier:Mécanisme d’ajustement court versus long terme 2.png|400px|vignette|centré]] | |||
Dans le graphique de l'entreprise, nous voyons que le nouveau prix du marché (P2) est supérieur au coût moyen (CM) et au coût marginal (Cm). Cela indique que l'entreprise est maintenant en mesure de réaliser un profit, représenté par la zone colorée entre le prix P2 et les courbes de coût. La différence entre le prix de vente et le coût moyen par unité sur la quantité produite représente le profit par unité. La réponse immédiate de l'entreprise à ce prix plus élevé sera d'augmenter la production pour maximiser ses profits, car chaque unité supplémentaire vendue au-dessus du coût marginal contribue au profit total. | |||
Sur le graphique du marché, la demande initiale (D1) croise l'offre à court terme (S1) au point A, établissant la quantité de marché initiale (q1) et le prix P1. Après le choc de la demande, la nouvelle courbe de demande (D2) se déplace vers la droite, indiquant que pour chaque prix, les consommateurs sont désormais prêts à acheter plus de biens. La nouvelle intersection de la demande avec l'offre à court terme se trouve au point B, où la quantité de marché a augmenté à q2 et le prix a augmenté à P2. | |||
Cette hausse du prix à court terme, de P1 à P2, reflète la réponse immédiate du marché à l'accroissement de la demande. Le prix plus élevé entraîne des profits économiques positifs pour les entreprises (P2 > CM), illustrés par le profit sur le graphique de l'entreprise. Cependant, cette situation est temporaire à court terme. À long terme, ces profits économiques positifs (<math>\pi > 0</math>) attireront de nouvelles entreprises sur le marché, augmentant l'offre et exerçant une pression à la baisse sur les prix. En conséquence, la courbe d'offre à long terme devrait s'ajuster vers la droite jusqu'à ce que le prix revienne au niveau où les profits économiques sont nuls (<math>p = CM</math>), rétablissant ainsi l'équilibre à long terme où les entreprises ne gagnent qu'un retour normal sur leur investissement. | |||
En | En bref, à court terme, l'entreprise peut profiter de prix plus élevés et de profits accrus. Cependant, la dynamique à long terme du marché, influencée par la libre entrée et sortie des entreprises, tend à éroder ces profits et à ramener le marché à un nouvel équilibre où les profits économiques sont nuls et le prix correspond au coût moyen de toutes les entreprises. | ||
=== Le profit économique de court terme attire des nouvelles entreprises dans le marché === | |||
Ces deux graphiques qui illustrent la réponse de long terme d'une entreprise et d'un marché à un choc de demande positif. | |||
[[Fichier:Mécanisme d’ajustement court versus long terme 3.png|400px|vignette|centré]] | |||
Le premier graphique montre la situation d'une entreprise individuelle. On y voit que le coût marginal (Cm) et le coût moyen (CM) restent inchangés par rapport à la situation initiale, indiquant que les coûts de production n'ont pas changé à long terme. Le prix sur le marché pour l'entreprise est de retour à P1, ce qui suggère que les profits à court terme qui étaient présents à cause du prix élevé P2 ont été érodés par l'entrée de nouvelles entreprises sur le marché. | |||
Le second graphique illustre la situation sur le marché dans son ensemble. À la suite du choc de demande initial qui a déplacé la courbe de demande de D1 à D2, le prix a augmenté de P1 à P2 et la quantité de marché de q1 à q2. En réponse à ces profits économiques temporaires, de nouvelles entreprises sont entrées sur le marché, ce qui a déplacé l'offre de court terme de S1 à S2. L'accroissement de l'offre a exercé une pression à la baisse sur les prix, conduisant à un nouveau point d'équilibre à long terme au point C, où le prix est redescendu à P1 et la quantité a augmenté à q3. | |||
À long terme, la courbe d'offre s'est déplacée vers la droite de S1 à S2 en raison de l'entrée de nouvelles entreprises, qui ont été attirées sur le marché par les profits économiques réalisés lorsque les prix étaient à P2. L'ajustement de l'offre continue jusqu'à ce que le prix sur le marché revienne au niveau où les entreprises ne font que couvrir leurs coûts, éliminant ainsi les profits économiques et ramenant le prix au niveau du coût moyen. À ce stade, le marché est de retour à un état d'équilibre où les entreprises existantes et nouvelles opèrent sans réaliser de profit économique (<math>\pi = 0</math>), car le prix est égal au coût moyen (<math>p = CM</math>), ce qui est caractéristique de la concurrence parfaite à long terme. | |||
L'offre de long terme dans le graphique du marché reste horizontale, indiquant que le marché à long terme peut toujours absorber des quantités supplémentaires au prix d'équilibre sans que cela n'entraîne de variation de prix. Cela reflète une condition d'entrée libre et parfaite sur le marché et l'ajustement des entreprises aux conditions de marché de sorte que seul un retour normal sur investissement est réalisé. | |||
= Résumé = | = Résumé = | ||
Dans un marché compétitif, le revenu total d'une entreprise est directement lié au volume de sa production, car elle est considérée comme un "preneur de prix" — c'est-à-dire qu'elle n'a pas la capacité d'influencer le prix du marché par ses propres actions. Le prix auquel elle vend son produit est à la fois son revenu moyen par unité vendue et son revenu marginal pour la dernière unité vendue. Pour maximiser ses profits, l'entreprise ajuste sa production jusqu'à ce que son coût marginal égale ce prix de marché donné. Ainsi, la courbe de coût marginal de l'entreprise correspond à sa courbe d'offre à court terme. | |||
À court terme, une entreprise peut se retrouver dans une situation où elle ne peut pas couvrir ses coûts fixes en raison de contraintes opérationnelles ou contractuelles. Si le prix de marché tombe en dessous du coût variable moyen, cela signifie que l'entreprise ne peut même pas couvrir ses coûts variables en produisant. Dans ce cas, il serait plus rationnel pour l'entreprise de cesser temporairement sa production plutôt que de continuer à opérer à perte. | |||
À long terme, cependant, une entreprise a la flexibilité de modifier sa structure de coûts et sa capacité de production. Les coûts fixes deviennent variables, car ils peuvent être ajustés grâce à des décisions d'investissement ou de désinvestissement. Une entreprise décidera de quitter le marché si le prix est inférieur au coût moyen, ce qui signifie qu'elle ne peut pas réaliser de profit, même en couvrant tous ses coûts variables et fixes. | |||
Lorsque l'entrée et la sortie des entreprises sur le marché sont libres et sans obstacle, on atteint un équilibre à long terme où les profits économiques des entreprises sont nuls, et les entreprises opèrent à leur efficacité minimale des échelles (EME), qui est le point où le coût moyen est à son minimum. Cependant, si les fonctions de coût varient d'une entreprise à l'autre en raison de différences dans l'efficacité, l'accès aux technologies, la qualité des intrants, ou d'autres facteurs, certaines entreprises peuvent réaliser des profits positifs même à long terme, tandis que d'autres pourraient opérer à l'équilibre ou même subir des pertes. | |||
Cet état reflète un marché en parfait équilibre, où le prix permet juste de couvrir le coût de production de l'entreprise la moins efficace qui reste sur le marché. Les entreprises plus efficaces que cette dernière peuvent réaliser des profits économiques, tandis que les moins efficaces ne peuvent pas survivre et quittent le marché. | |||
= Annexes = | = Annexes = | ||
| Ligne 496 : | Ligne 419 : | ||
[[Catégorie:Federica Sbergami]] | [[Catégorie:Federica Sbergami]] | ||
[[Catégorie:Giovanni Ferro-Luzzi]] | [[Catégorie:Giovanni Ferro-Luzzi]] | ||
Version actuelle datée du 22 janvier 2024 à 07:34
Basé sur un cours de Federica Sbergami[1][2][3]
Principes et concepts de la microéconomie ● Approche méthodologiques au cours d'introduction à la microéconomie ● Les forces du marché : l'offre et la demande ● Les élasticités et ses applications ● Offre, demande et politiques gouvernementales ● Surplus du consommateur et du producteur ● Les externalités et le rôle de l'État ● Principes et Dilemmes des Biens Publics dans l'Économie de Marché ● Les coûts de production ● Les entreprises en concurrence parfaite ● Les entreprises en monopole ● Concurrence monopolistique ● Oligopole ● Contrainte et préférences du consommateur ● Choix du consommateur ● Les problèmes d'information et les choix publics
L'analyse des structures de marché en économie révèle deux types principaux : les marchés compétitifs et les marchés non compétitifs. Dans les marchés compétitifs, on trouve un grand nombre d'entreprises, où chacune a peu ou pas d'influence sur le prix du marché. Ces entreprises sont considérées comme des "priseurs de prix", acceptant le prix déterminé par le marché. Le rôle des fonctions de coût de production est crucial dans ces marchés, influençant fortement les décisions des entreprises en matière de production et les quantités produites. Ces décisions sont basées sur la maximisation du profit, où les entreprises cherchent à équilibrer les coûts et les revenus. L'équilibre du marché est atteint lorsque l'offre globale rencontre la demande globale, déterminant ainsi le prix du marché.
En contraste, les marchés non compétitifs sont caractérisés par la présence d'entreprises ayant un pouvoir de marché significatif. Cela leur permet d'influencer les prix en ajustant leur niveau de production. Ces marchés comprennent des structures telles que les monopoles, où un seul vendeur domine, les oligopoles, caractérisés par quelques entreprises influentes, et la concurrence monopolistique, où plusieurs entreprises vendent des produits différenciés. Dans ces marchés, les entreprises ont la capacité d'affecter les prix sur le marché, contrairement aux marchés compétitifs où le prix est un résultat de l'équilibre entre l'offre et la demande.
La notion de marché compétitif en économie est centrée sur l'idée d'une concurrence parfaite, où la structure du marché se définit par plusieurs caractéristiques distinctes. Dans un tel marché, on trouve une infinité de vendeurs et d'acheteurs, chacun ayant une part de marché extrêmement réduite. Cette configuration implique que la taille de chaque acteur économique est insignifiante par rapport à la taille totale du marché. En conséquence, aucun vendeur ou acheteur n'est en mesure d'influencer le prix du marché par ses actions individuelles, que ce soit en modifiant les quantités achetées ou vendues.
Un marché compétitif se caractérise également par trois conditions principales. Premièrement, le bien vendu sur ce marché est homogène, signifiant qu'il y a peu ou pas de différence entre les produits offerts par différents producteurs. Cette homogénéité garantit que les consommateurs ne privilégient pas un vendeur par rapport à un autre en raison de la qualité ou des caractéristiques du produit.
Deuxièmement, la présence d'un grand nombre d'acheteurs et de vendeurs est cruciale. Cette multiplicité d'acteurs garantit que l'influence individuelle de chaque vendeur ou acheteur sur le prix du marché est minime, voire négligeable.
Troisièmement, un marché compétitif se caractérise par une libre entrée et sortie des acteurs sur le marché. Cela signifie qu'il n'existe pas de barrières significatives empêchant de nouveaux vendeurs ou acheteurs de participer au marché ou les acteurs existants de le quitter.
Le résultat de ces conditions est qu'aucun acteur, qu'il soit acheteur ou vendeur, ne peut influencer le prix du marché. Dans ce contexte, tous les participants sont des 'preneurs de prix' (price takers), acceptant le prix du marché tel qu'il est déterminé par les forces globales de l'offre et de la demande. Ce modèle de marché est souvent utilisé comme idéal théorique pour analyser et comparer d'autres structures de marché moins compétitives, où certains acteurs peuvent exercer une influence significative sur les prix.
Maximisation du profit[modifier | modifier le wikicode]
La maximisation du profit est un concept central en économie et en gestion d'entreprise, représentant l'objectif principal des entreprises dans une économie de marché. Cette notion se fonde sur l'effort des entreprises pour obtenir la plus grande différence positive possible entre leurs revenus et leurs coûts.
Les revenus totaux d'une entreprise sont déterminés par le volume de ses ventes et le prix de ses produits ou services. Les entreprises s'efforcent d'accroître ces revenus en augmentant soit la quantité de produits vendus, soit le prix de ces produits, ou les deux. Parallèlement, elles doivent gérer leurs coûts totaux, qui incluent à la fois les coûts fixes, tels que le loyer et les salaires, qui ne changent pas quelle que soit la production, et les coûts variables, qui varient en fonction du niveau de production, comme les matières premières.
Le profit est la différence entre les revenus totaux et les coûts totaux. Une entreprise maximise son profit en trouvant le point où cette différence est maximale. Cette recherche de maximisation du profit influence toutes les décisions clés de l'entreprise, y compris les stratégies de production, de tarification, d'investissement et de marketing. Les décisions sont souvent prises sur la base d'une analyse marginale, qui examine l'impact sur les revenus et les coûts d'une augmentation ou d'une diminution de l'unité de production ou de vente. L'objectif est de continuer la production jusqu'à ce que le coût de production d'une unité supplémentaire soit égal au revenu généré par cette unité.
Le contexte du marché joue un rôle crucial dans la capacité d'une entreprise à maximiser ses profits. Dans un marché hautement concurrentiel, par exemple, les entreprises peuvent être limitées dans leur capacité à fixer des prix élevés, tandis que dans des marchés moins concurrentiels, comme les monopoles, elles peuvent avoir plus de liberté pour augmenter leurs profits.
La recette[modifier | modifier le wikicode]
Le profit (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi} ) d'une entreprise est la différence entre sa recette totale (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RT} ) et son coût total (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CT} ). La recette totale est calculée comme le produit du prix par la quantité vendue, c'est-à-dire Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RT = \text{Prix} \times \text{Quantité}} . Dans un marché compétitif, où le prix est déterminé par le marché et est donc constant pour chaque entreprise, la recette totale est directement proportionnelle à la quantité vendue (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q} ).
La recette moyenne (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RM} ) indique le revenu qu’une entreprise réalise en moyenne par unité vendue. Elle est calculée comme Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RM = \frac{RT}{\text{Quantité}}} . Puisque Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RT = \text{Prix} \times \text{Quantité}} , la recette moyenne se simplifie en Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RM = \text{Prix}} . Cela signifie que, dans un marché compétitif, la recette moyenne est égale au prix du produit.
La recette marginale (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Rm} ) est un concept clé pour comprendre comment les variations dans les quantités vendues affectent la recette totale. Elle est définie comme l'augmentation de la recette totale résultant de la vente d'une unité supplémentaire. Mathématiquement, cela se traduit par , ou, pour des variations infiniment petites, . Dans un marché compétitif, où le prix est constant, la recette marginale est égale au prix du bien, donc .
En somme, dans un marché compétitif, la structure de prix fixe et uniforme simplifie considérablement le calcul des recettes. L'égalité de la recette marginale et du prix est un élément crucial qui influence la décision de l’entreprise concernant la quantité à produire pour maximiser son profit.
Le profit[modifier | modifier le wikicode]
Le profit () d'une entreprise dépend de la quantité () produite. Pour une entreprise opérant dans un marché concurrentiel, le profit peut être exprimé comme la différence entre la recette totale (RT) et le coût total (CT) en fonction de la quantité, soit : où Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} est le prix du bien, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CF} représente les coûts fixes et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CV(q)} les coûts variables en fonction de la quantité.
Le profit moyen (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi_M} ) est la différence entre la recette moyenne (RM) et le coût moyen (CM) en fonction de la quantité : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi_M(q) = RM - CM(q) = p - CFM - CVM(q)}
Le profit marginal (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi_m} ) est la différence entre la recette marginale (Rm) et le coût marginal (Cm) en fonction de la quantité : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi_m(q) = Rm - Cm(q) = p - Cm(q)}
Le profit est maximisé lorsque le coût marginal est égal à la recette marginale. Ceci est exprimé par la condition de maximisation du profit : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \text{max} \pi(q) = RT(q) - CT(q)}
La condition de premier ordre (CPO) pour maximiser le profit est que la dérivée première du profit par rapport à la quantité doit être égale à zéro. Mathématiquement, cela s'exprime comme suit : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {\partial \pi}{\partial q} = \frac {\partial RT}{\partial q} - \frac {\partial CT}{\partial q} = Rm - Cm = p - Cm = 0}
À l'optimum, la recette marginale (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Rm} ), qui est égale au prix (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} ), est égale au coût marginal (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Cm} ). Cette égalité est fondamentale dans la théorie de la production et de la maximisation du profit dans un contexte de concurrence parfaite.
Maximisation du π : un exemple numérique[modifier | modifier le wikicode]
L'exemple numérique fourni dans le tableau démontre comment une entreprise détermine le niveau de production qui maximise son profit. Dans cet exemple, l'entreprise vend son produit à un prix fixe de 6 euros par litre, ce qui se reflète dans la recette totale qui augmente de 6 euros pour chaque litre supplémentaire vendu. La ligne du coût total indique que l'entreprise a des coûts initiaux même sans production, qui pourraient être des coûts fixes tels que le loyer ou les salaires, et que le coût de production de chaque litre supplémentaire augmente, probablement en raison de l'augmentation des coûts variables.
En observant la progression du profit total, on constate qu'il augmente avec chaque litre produit jusqu'à la production de 4 ou 5 litres, après quoi le profit commence à diminuer. Ce phénomène suggère que, bien que l'entreprise continue à recevoir 6 euros pour chaque litre supplémentaire (comme l'indique la recette marginale constante), les coûts de production de chaque litre supplémentaire augmentent à un rythme plus rapide, ce qui est évident dans les chiffres croissants du coût marginal.
Le profit marginal, qui est l'augmentation du profit total résultant de la vente d'une unité supplémentaire, commence à décliner après la production de 5 litres, devenant négatif au-delà de ce point. Cela signifie que la production de plus de 5 litres réduit le profit global de l'entreprise, car le coût de production de ces litres supplémentaires est supérieur au revenu qu'ils génèrent.
La maximisation du profit se produit lorsque le profit marginal est égal à zéro, ce qui se produit à 5 litres dans cet exemple. À ce niveau, le coût marginal, l'augmentation du coût total due à la production d'un litre supplémentaire, est exactement égal à la recette marginale, ce qui indique que l'entreprise ne gagne ni ne perd de profit supplémentaire sur le dernier litre produit. Selon la condition de premier ordre pour la maximisation du profit, c'est à ce point que l'entreprise devrait arrêter d'augmenter sa production pour maximiser son profit.
En résumé, cet exemple illustre clairement la relation entre la recette marginale, le coût marginal et la maximisation du profit. Il démontre également que pour maximiser son profit, une entreprise dans un marché compétitif doit produire jusqu'à ce que le coût marginal de production égale la recette marginale obtenue de la vente d'une unité supplémentaire, et c'est à ce point que le profit total est maximisé.
Maximisation du π : analyse graphique[modifier | modifier le wikicode]
La maximisation du profit (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi} ) par une entreprise peut être illustrée de manière graphique, ce qui permet de visualiser comment les décisions de production sont prises en fonction de la logique marginale.
Dans un graphique typique, la quantité produite est placée sur l'axe horizontal (l'axe des abscisses), tandis que la recette totale (RT), le coût total (CT), et le profit sont placés sur l'axe vertical (l'axe des ordonnées). La recette totale est généralement représentée par une ligne droite qui commence à l'origine (si le prix est constant), car la recette totale est simplement le prix multiplié par la quantité. Le coût total commence généralement au-dessus de l'origine, représentant les coûts fixes, et courbe vers le haut à mesure que la quantité augmente, reflétant l'augmentation des coûts variables.
La quantité qui maximise le profit, notée Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} , est là où l'écart entre la recette totale et le coût total est le plus grand. Graphiquement, c'est le point où la pente de la recette totale (qui est la recette marginale, Rm) est égale à la pente du coût total (qui est le coût marginal, Cm). À ce point, toute augmentation supplémentaire de la quantité produite ne ferait qu'ajouter autant de coûts que de revenus, ne contribuant ainsi pas au profit.
Sur le graphique, la ligne de recette marginale coupe la ligne de coût marginal exactement à ce point optimal Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} . Avant ce point, la recette marginale excède le coût marginal, ce qui signifie que la production d'une unité supplémentaire ajoute plus au revenu qu'elle n'ajoute aux coûts, et donc le profit augmente. Après ce point, le coût marginal excède la recette marginale, donc la production d'une unité supplémentaire coûte plus qu'elle ne rapporte en termes de revenu, et le profit diminue.
La décision de la firme de produire la quantité Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} reflète donc la logique marginale : continuer à produire tant que le revenu supplémentaire (Rm) est supérieur au coût supplémentaire (Cm) et s'arrêter là où ils sont égaux. C'est la quintessence de la maximisation du profit dans la théorie économique classique, et elle est souvent représentée dans un graphique par la tangence de la courbe de recette totale avec la courbe de coût total.
Ce graphique illustre l'analyse graphique de la maximisation du profit pour une entreprise dans un marché compétitif.
Le graphique montre deux lignes principales : une ligne horizontale verte représentant le prix (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} ), qui est également la recette moyenne (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RM} ) et la recette marginale (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Rm} ), et une ligne rouge ascendante représentant le coût marginal (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Cm} ) en fonction de la quantité produite.
Point de Maximisation du Profit (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} ) : Sur ce graphique, le point de maximisation du profit, noté Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} , est là où la ligne de coût marginal (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Cm} ) croise la ligne de recette marginale (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Rm} ). C'est le niveau de production où la recette supplémentaire générée par la vente d'une unité supplémentaire est exactement égale au coût supplémentaire de la production de cette unité. À ce point, l'entreprise maximise son profit, car toute production supplémentaire au-delà de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} entraînerait des coûts marginaux supérieurs aux recettes marginales, réduisant ainsi le profit.
Recette et Coût Marginal : Le fait que la ligne de recette marginale soit horizontale indique que le prix de vente du produit reste constant, indépendamment de la quantité vendue, ce qui est typique d'une entreprise en concurrence parfaite. Le coût marginal, cependant, augmente avec la quantité, indiquant que la production de chaque unité supplémentaire coûte plus cher que la précédente.
Zones de Profit : La zone ombrée entre les quantités Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q_1} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} représente le profit total réalisé par l'entreprise. C'est la différence entre la recette totale et le coût total pour cette plage de production.
Le graphique démontre clairement l'importance du coût marginal et de la recette marginale dans la prise de décision pour une entreprise compétitive. La règle de maximisation du profit est suivie lorsque l'entreprise produit à un niveau où le coût marginal est égal à la recette marginale. Produire moins que Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} signifierait que l'entreprise ne profite pas pleinement de sa capacité à générer du profit, tandis que produire plus que Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} signifierait que l'entreprise subirait des coûts marginaux qui réduisent le profit global.
Il est également important de noter que si le coût marginal était inférieur à la recette marginale au-delà de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} , l'entreprise pourrait augmenter sa production pour augmenter son profit. Inversement, si le coût marginal augmente brusquement ou si le prix du marché diminue, cela pourrait conduire à une réduction de la quantité optimale de production.
Cet exemple graphique sert de modèle de base pour comprendre la prise de décision dans les entreprises compétitives, en assumant que les conditions de marché sont constantes et que l'entreprise est un preneur de prix, sans pouvoir d'influence sur le prix du marché.
Cm versus CM[modifier | modifier le wikicode]
L'entreprise cherche à maximiser ses profits en se focalisant sur les coûts et recettes marginaux plutôt que sur les moyennes. Le raisonnement à la marge implique la considération des coûts et des bénéfices supplémentaires liés à la production et à la vente d'une unité supplémentaire.
Le coût marginal (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Cm} ) représente le coût de production d'une unité supplémentaire de bien ou de service. Il est crucial dans la prise de décision car si le revenu supplémentaire (recette marginale) généré par la vente de cette unité est supérieur au coût marginal de sa production, l'entreprise augmente son profit en produisant cette unité supplémentaire.
En revanche, le coût moyen (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CM} ) représente le coût total divisé par le nombre d'unités produites. Il donne une indication du coût par unité mais ne reflète pas nécessairement les coûts liés à la production d'une unité supplémentaire.
Si une entreprise se concentre uniquement sur la maximisation du profit moyen, noté Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q_{\pi M}} , et s'arrête de produire à ce niveau, elle pourrait manquer l'opportunité de réaliser des bénéfices supplémentaires. La quantité qui maximise le profit moyen n'est pas nécessairement la même que celle qui maximise le profit total. En effet, tant que le coût marginal est inférieur à la recette marginale, l'entreprise peut augmenter son profit en augmentant sa production.
L'objectif est donc de trouver le point où le coût marginal est égal à la recette marginale, ce qui est la condition pour maximiser le profit total. Arrêter la production au point où le profit moyen est maximisé pourrait signifier que l'entreprise ne produit pas suffisamment pour atteindre le point où le profit total est à son apogée. Cela peut être visualisé sur un graphique où le profit total continue d'augmenter jusqu'au point où le coût marginal croise la recette marginale, même si le profit moyen a déjà atteint son maximum à un niveau inférieur de production.
Ce graphique représente les courbes de coût et de revenu d'une entreprise, qui sont essentielles à la compréhension de la prise de décisions en matière de production pour maximiser le profit. On y voit trois courbes distinctes : la courbe de coût moyen (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CM} ), la courbe de coût marginal (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Cm} ) et une ligne horizontale qui représente à la fois le prix (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} ), la recette moyenne (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RM} ) et la recette marginale (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Rm} ), qui sont identiques dans un marché parfaitement concurrentiel où le prix est constant indépendamment de la quantité vendue.
Le point où la courbe de coût marginal coupe la ligne de prix (et donc la recette marginale), noté Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} , est le niveau de production qui maximise le profit. À ce point, le coût supplémentaire de production d'une unité supplémentaire (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Cm} ) est exactement égal au revenu supplémentaire que l'entreprise reçoit pour cette unité (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Rm} ). Si l'entreprise produit plus ou moins que Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} , elle ne maximise pas ses profits : produire moins signifierait ne pas profiter de tous les revenus supplémentaires possibles, tandis que produire plus augmenterait les coûts plus rapidement que les revenus.
La courbe de coût moyen (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CM} ) atteint généralement son minimum avant d'augmenter à nouveau, ce qui est dû aux économies d'échelle et ensuite aux déséconomies d'échelle. Le point où le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CM} est le plus bas n'est pas le point qui maximise les profits, bien qu'il soit souvent interprété à tort comme tel. Ce point est noté Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q_{\pi M}} sur le graphique et représente la quantité qui maximise le profit moyen, pas le profit total. Si une entreprise choisissait de produire à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q_{\pi M}} , elle produirait là où le coût moyen par unité est le plus bas, mais cela ne prend pas en compte les bénéfices marginaux de la production de quantités supplémentaires jusqu'à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} .
En conclusion, l'analyse graphique montre clairement pourquoi une entreprise devrait se concentrer sur les coûts et les revenus marginaux lors de la prise de décisions de production. L'objectif n'est pas de minimiser le coût moyen ou de maximiser le profit moyen, mais plutôt de trouver le point où le coût marginal de production d'une unité supplémentaire est égal au revenu supplémentaire généré par la vente de cette unité, ce qui se produit au niveau de production Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} . C'est à ce niveau que le profit total de l'entreprise est maximisé.
Maximisation du π : vue d'ensemble[modifier | modifier le wikicode]
Le graphique présenté offre une vue d'ensemble complexe et détaillée de la maximisation du profit (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi} ) dans le cadre de la théorie économique de la firme. Plusieurs courbes clés sont représentées pour illustrer les différentes dimensions des coûts et des recettes d'une entreprise.
On observe tout d'abord les courbes de coût total (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CT} ), de recette totale (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RT} ), et de profit (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi} ) en fonction de la quantité (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Q} ). La courbe de coût total commence au-dessus de l'origine, au niveau des coûts fixes (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CF} ), et augmente avec la quantité produite. La courbe de recette totale débute à l'origine et s'élève également, mais à un taux constant, reflétant un prix de vente (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle P} ) constant par unité vendue.
La différence entre les recettes totales et les coûts totaux à chaque niveau de production génère la courbe de profit, qui atteint son maximum (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi_{max}} ) au point où la quantité produite est Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Q^*} . Ce point représente la quantité qui maximise le profit total de l'entreprise. La maximisation du profit se produit lorsque la pente de la courbe de recette totale (la recette marginale, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Rm} ) est égale à la pente de la courbe de coût total (le coût marginal, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Cm} ). Graphiquement, c'est là où les deux courbes se croisent.
En dessous de cette intersection, le profit marginal est positif, ce qui signifie que produire une unité supplémentaire augmente le profit total. Au-delà de ce point, le profit marginal devient négatif, ce qui indique que produire des unités supplémentaires réduit le profit total. C'est également le point où le coût marginal devient supérieur au prix et donc à la recette marginale, ce qui explique pourquoi la production supplémentaire n'est pas profitable.
Les "points morts" indiqués sur le graphique correspondent aux niveaux de production où le profit est nul. Ces points sont situés là où la courbe de coût total coupe la courbe de recette totale. Entre ces deux points, l'entreprise réalise un profit; en dehors de ces points, l'entreprise subit des pertes.
La courbe de coût moyen (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CM} ) atteint un minimum avant d'augmenter, ce qui reflète les économies d'échelle suivies des déséconomies d'échelle. Le point où la courbe de coût moyen coupe la ligne de prix est le point où le profit moyen est maximisé. Cependant, ce n'est pas le but principal de l'entreprise, qui cherche à maximiser le profit total, pas le profit moyen.
Le graphique montre ainsi l'importance cruciale de la prise de décision basée sur les coûts et recettes marginaux plutôt que moyens. Il illustre la manière dont la prise en compte des coûts marginaux, en particulier, guide l'entreprise vers le niveau de production optimal qui maximise le profit total. Cela souligne également la nature dynamique des coûts dans la production et la manière dont l'analyse marginale permet d'optimiser la performance financière d'une entreprise.
Profit[modifier | modifier le wikicode]
Le profit maximum d'une entreprise est atteint lorsque la différence entre la recette totale (RT) et le coût total (CT) est la plus grande. Ce point est identifié par la quantité Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} , où les décisions marginales de production rencontrent l'équilibre parfait entre coûts additionnels et revenus additionnels.
Le profit (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi} ) peut être exprimé de différentes manières, mais fondamentalement, il est la différence entre la recette totale et le coût total à la quantité qui maximise le profit, soit Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi = RT - CT} . La recette totale est le produit du prix de vente par unité (p), qui est également la recette moyenne (RM) dans un marché concurrentiel, et la quantité vendue (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q} ), d'où Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RT = RM \times q} . Le coût total peut être décomposé en coût moyen (CM) multiplié par la quantité, soit Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CT = CM \times q} .
En soustrayant le coût total de la recette totale, le profit peut aussi être formulé en termes de recette et de coût par unité, ce qui donne Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi = (RM \times q) - (CM \times q)} . Comme le prix de vente par unité est égal à la recette moyenne dans un marché parfaitement concurrentiel, c'est-à-dire Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RM = p} , et en factorisant par la quantité Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q} , on obtient Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi = (p - CM) \times q} . Cette expression montre que le profit est également la différence entre le prix et le coût moyen par unité, multipliée par le nombre d'unités vendues.
Cela indique que pour maximiser les profits, l'entreprise doit non seulement considérer le coût et la recette par unité, mais aussi l'impact de la production sur ces coûts et recettes à la marge. En pratique, cela implique de continuer à produire jusqu'à ce que le coût de production d'une unité supplémentaire (coût marginal) soit égal au revenu généré par la vente de cette unité (recette marginale), ce qui est le fondement de la prise de décision en termes de maximisation du profit.
Ce graphique illustre un modèle économique classique de maximisation du profit dans un marché concurrentiel. Il montre les relations entre le coût marginal (Cm), le coût moyen (CM), la recette moyenne (RM), qui est également égale à la recette marginale (Rm) et au prix de vente (p), en fonction de la quantité produite (Q).
La ligne horizontale représente le prix de vente (p) par unité, qui, dans un marché parfaitement concurrentiel, est égal à la recette moyenne (RM) ainsi qu'à la recette marginale (Rm). Cette horizontalité indique que le prix est constant quel que soit le niveau de production ; il est déterminé par le marché et est le même pour toutes les unités vendues.
La courbe de coût moyen (CM) descend, atteint un minimum, puis remonte, ce qui reflète généralement les économies d'échelle réalisées jusqu'à un certain point, après lequel les déséconomies d'échelle commencent à se manifester. La courbe de coût marginal (Cm) croise la courbe de coût moyen (CM) à son point le plus bas, ce qui est typique dans la théorie économique car le coût marginal coupe le coût moyen à son minimum.
Le point où la courbe de coût marginal (Cm) croise la ligne du prix de vente (p), noté q*, est le niveau de production qui maximise le profit de l'entreprise. À cette quantité, le coût supplémentaire de production d'une unité supplémentaire est exactement égal au revenu supplémentaire généré par sa vente. Produire plus que q∗ entraînerait des coûts supplémentaires supérieurs aux revenus générés par la vente des unités supplémentaires, diminuant ainsi le profit total.
La surface en vert représente le profit total, qui est la zone entre la courbe des recettes totales et la courbe des coûts totaux. Ce profit est maximisé à la quantité q*, où la différence entre les recettes totales et les coûts totaux est la plus grande.
Ce graphique montre clairement l'importance de la prise de décision basée sur les coûts et recettes marginaux pour la maximisation du profit dans un marché concurrentiel. Il illustre comment les coûts moyens et marginaux évoluent avec la production et comment ces coûts doivent être pris en compte par les entreprises pour déterminer le niveau de production optimal.
Maximisation du π : un exemple analytique[modifier | modifier le wikicode]
Pour déterminer la quantité qui maximise le profit de l'entreprise lorsque le prix de marché est Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p = 13} , nous devons nous référer à la condition de premier ordre (CPO) où le coût marginal (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Cm} ) est égal au prix de marché. La fonction de coût est donnée par Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CT = 1 + 10q - q^2 + \frac{1}{3}q^3} . La dérivée de cette fonction par rapport à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q} donnera le coût marginal (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Cm} ), qui est égal à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 10 - 2q + q^2} . En égalisant le coût marginal au prix, nous avons Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 10 - 2q + q^2 = 13} .
Pour résoudre cette équation quadratique, nous appliquons la formule quadratique : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}} . Cela nous donne Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q = \frac{2 \pm \sqrt{4 - 4(1)(-3)}}{2} = \frac{2 \pm \sqrt{16}}{2}} . Les solutions de cette équation sont Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q = \frac{6}{2}} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q = \frac{-2}{2}} .
Cependant, nous excluons la solution négative car une quantité produite ne peut pas être négative, laissant Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q = 3} comme la quantité qui maximise le profit de l'entreprise.
Offre de la firme de court et de long terme[modifier | modifier le wikicode]
La courbe d’offre de l’entreprise à court terme[modifier | modifier le wikicode]
La courbe d'offre à court terme d'une entreprise dans un marché compétitif coïncide avec sa courbe de coût marginal au-dessus du point de fermeture, c'est-à-dire là où le coût marginal est supérieur au coût moyen variable. La raison en est qu'à court terme, l'entreprise doit couvrir au moins ses coûts variables pour continuer à fonctionner. Si le prix de marché est inférieur au coût variable moyen, l'entreprise choisira de ne pas produire et de minimiser ses pertes en couvrant seulement ses coûts fixes, qui sont inévitables à court terme.
La courbe de coût marginal est dérivée de la fonction de coût total et montre le coût additionnel de production d'une unité supplémentaire. À court terme, tant que le prix de marché est supérieur au coût marginal, l'entreprise continuera d'augmenter sa production car chaque unité supplémentaire vendue contribuera à couvrir les coûts fixes et à générer un profit. Lorsque le coût marginal est égal au prix de marché, l'entreprise maximise son profit car la production d'une unité supplémentaire n'apporterait ni profit ni perte supplémentaire.
À plus long terme, la courbe d'offre peut différer de la courbe de coût marginal en raison de l'entrée de nouvelles entreprises sur le marché ou de la sortie d'entreprises existantes, ce qui affecte les coûts totaux et variables, ainsi que la capacité de production globale. De plus, à long terme, les coûts fixes peuvent devenir variables, permettant à l'entreprise d'ajuster tous ses coûts en réponse aux changements du marché.
Le graphique montre les courbes de coût marginal (Cm) et de coût moyen (CM) d'une entreprise par rapport à la quantité produite. La courbe de coût marginal, qui est également étiquetée comme l'offre de court terme, est ascendante, indiquant que le coût de production d'une unité supplémentaire augmente avec la quantité produite. Ceci est conforme à la loi des rendements décroissants, où l'ajout de facteurs de production supplémentaires à un certain point entraîne une diminution du rendement marginal.
La courbe de coût moyen a une forme en U, suggérant que l'entreprise expérimente initialement des économies d'échelle à mesure que la production augmente (le coût moyen diminue), mais après avoir atteint un certain niveau de production (pas nécessairement montré dans ce graphique), les déséconomies d'échelle entraîneront une augmentation du coût moyen.
Deux prix de marché différents sont représentés, P1 et P2, avec P2 étant supérieur à P1. Ces prix coupent la courbe de coût marginal à deux points différents, définissant les quantités q1 et q2, respectivement, que l'entreprise est disposée à offrir à ces prix dans le cadre d'un marché compétitif. À P1, la quantité offerte est q1, tandis qu'à P2, la quantité offerte est q2. Cela démontre que l'offre de l'entreprise est directement liée au coût marginal de production.
Il est important de noter que l'offre de court terme de l'entreprise est représentée par la portion de la courbe de coût marginal qui se situe au-dessus de la courbe de coût moyen. Cela indique que l'entreprise ne fournira pas de biens sur le marché à un prix qui ne couvre pas au moins le coût moyen, car cela signifierait opérer à perte.
Le graphique illustre clairement que l'entreprise ajustera sa quantité offerte en réponse aux changements de prix du marché pour maximiser son profit. Lorsque le prix du marché augmente de P1 à P2, il devient rentable pour l'entreprise d'augmenter sa production de q1 à q2, car le prix de marché couvre le coût marginal de production des unités supplémentaires.
Décision de fermeture à court terme[modifier | modifier le wikicode]
La décision de fermeture à court terme pour une entreprise fait référence à la situation où l'entreprise doit décider si elle continue d'opérer ou si elle cesse ses activités en raison de pertes financières. À court terme, les coûts fixes (tels que le loyer, l'équipement et les salaires des employés permanents) ne peuvent pas être ajustés car ils sont engagés indépendamment de la production. Cela signifie que, même si l'entreprise cesse de produire, ces coûts fixes doivent toujours être payés.
Le coût variable moyen (CVM) représente le coût moyen des variables de production par unité de bien ou de service produite. Dans un contexte de court terme, si le prix du marché est inférieur au coût variable moyen, l'entreprise subit une perte sur chaque unité produite. Dans ce cas, il serait plus judicieux pour l'entreprise de cesser la production, car la perte résultant de la production serait plus grande que les coûts fixes seuls. En d'autres termes, il est préférable pour l'entreprise de subir une perte égale aux coûts fixes plutôt que de subir des pertes encore plus importantes en couvrant également les coûts variables.
La règle générale est que si le prix de marché est supérieur au coût variable moyen, l'entreprise devrait continuer à produire à court terme, même si elle subit des pertes totales, car en produisant, elle peut couvrir une partie de ses coûts fixes et réduire la perte globale. Si le prix est inférieur au coût variable moyen, l'entreprise devrait envisager de fermer temporairement car chaque unité produite augmente la perte totale.
La décision de continuer à opérer ou de fermer temporairement est donc fortement influencée par la relation entre le prix de marché et le coût variable moyen à court terme.
Le graphique illustre la prise de décision d'une entreprise concernant la production à court terme en fonction des coûts et du prix de vente. Il montre trois courbes : la courbe de coût marginal (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Cm} ), qui représente également l'offre de court terme de l'entreprise, la courbe de coût moyen (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CM} ), et la courbe de coût variable moyen (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CVM} ).
Selon le graphique, il y a trois décisions possibles pour l'entreprise en fonction du prix de marché (noté ici comme Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p^{SF}} , le prix de vente à court terme) :
- Si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p^{SF}} est supérieur au coût moyen (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CM} ) : L'entreprise produit et réalise un profit, car le prix de vente couvre à la fois les coûts variables et fixes par unité produite.
- Si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p^{SF}} est inférieur au coût variable moyen minimum (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CVM_{\text{min}}} ) : L'entreprise décide de ne rien produire et de fermer temporairement car le prix de vente ne couvre même pas les coûts variables. À court terme, les coûts fixes sont considérés comme perdus car ils ne dépendent pas de la décision de produire.
- Si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p^{SF}} est supérieur au Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CVM_{\text{min}}} mais inférieur au Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CM} : L'entreprise continue à produire à court terme malgré des pertes opérationnelles, car le prix de vente couvre les coûts variables et contribue partiellement aux coûts fixes. Il s'agit d'une situation où la production permet de minimiser les pertes en comparaison avec une fermeture complète.
La courbe de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CVM} montre la baisse des coûts variables unitaires avec l'augmentation de la production jusqu'à un certain point, après quoi les coûts variables par unité commencent à augmenter en raison des déséconomies d'échelle.
L'intersection de la courbe de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Cm} avec la courbe de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CM} détermine le seuil de rentabilité à long terme, où l'entreprise couvre tous ses coûts et commence à réaliser des profits si le prix de marché est égal ou supérieur à ce niveau. En dessous de ce seuil, l'entreprise peut continuer à fonctionner à court terme tant que le prix de marché reste supérieur au Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CVM} .
Le graphique souligne l'importance de la distinction entre les décisions à court et à long terme. À court terme, les coûts fixes sont irrécupérables et l'entreprise vise à couvrir ses coûts variables tout en contribuant au maximum aux coûts fixes. À long terme, tous les coûts deviennent variables, et l'entreprise devra considérer la rentabilité globale pour sa survie et sa décision de rester sur le marché.
L'entreprise fait face à un choix crucial en période de conditions de marché défavorables : continuer à produire ou arrêter la production. La décision dépend de la comparaison entre les profits (ou les pertes réduites) réalisés en produisant par rapport à ceux en cessant toute production.
Si l'entreprise ne produit pas, la quantité produite est nulle (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q = 0} ), et le profit (ou plutôt la perte, car les coûts fixes doivent toujours être payés même si rien n'est produit) est simplement le négatif des coûts fixes (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi(0) = -CF} ). En revanche, si l'entreprise produit une quantité positive Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q = q^*} , le profit est la différence entre la recette totale (le prix de marché multiplié par la quantité produite) et la somme des coûts variables et des coûts fixes (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi(q^*) = pq^* - CV(q^*) - CF} ).
L'entreprise choisira de produire une quantité positive si le profit de produire Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} est supérieur au profit de ne rien produire, c'est-à-dire si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi(q^*) > \pi(0)} . Cela se traduit par la condition où le revenu total de la production dépasse les coûts variables (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle pq^* > CV(q^)} ), ou, en d'autres termes, si le prix de marché est supérieur au coût variable moyen à la quantité Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q^*} (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p > CVM(q^*)} ).
En période de difficultés, l'entreprise pourrait donc continuer à produire tant que le prix de marché est supérieur au coût variable moyen minimum (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CVM_{min}} ), définissant ainsi le seuil de fermeture. Ce seuil est le niveau de prix minimum nécessaire pour que l'entreprise couvre ses coûts variables. Si le prix du marché est inférieur à ce seuil, il serait plus rationnel pour l'entreprise de cesser la production pour minimiser ses pertes, car même les coûts variables ne seraient pas couverts.
En résumé, l'entreprise continue à produire au-dessus du seuil de fermeture pour réduire ses pertes, même si elle opère à perte, car elle contribue au moins partiellement à la couverture des coûts fixes, ce qui est préférable à ne pas produire du tout et à payer l'intégralité des coûts fixes sans aucun revenu pour compenser.
Le graphique présente la relation entre les coûts d'une entreprise et le prix de marché, illustrant la prise de décision en termes de production et de fermeture à court terme. Il montre les courbes de coût marginal (Cm), de coût moyen (CM) et de coût variable moyen (CVM), ainsi que le seuil de fermeture.
La courbe de coût marginal (Cm) est ascendante, indiquant que le coût de production d'une unité supplémentaire augmente avec chaque unité produite. La courbe de coût moyen (CM) a une forme en U typique, indiquant des économies d'échelle jusqu'à un certain point (le minimum de la courbe CM), après quoi les coûts moyens commencent à augmenter à cause des déséconomies d'échelle.
Trois prix de marché différents sont indiqués : P2, P1 et le seuil de fermeture (PsF).
- À P2, le profit est positif (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi > 0} ) car le prix de marché est supérieur au coût moyen et au coût marginal, ce qui signifie que l'entreprise couvre tous ses coûts et réalise un bénéfice.
- À P1, l'entreprise subit des pertes d'exploitation (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -CF < \pi < 0} ) car le prix de marché couvre les coûts variables mais pas la totalité des coûts fixes. Toutefois, tant que le prix est au-dessus du seuil de fermeture, il est plus avantageux pour l'entreprise de continuer à produire à court terme plutôt que de fermer complètement, car les recettes générées contribuent aux coûts fixes.
- Le seuil de fermeture (PsF) est le prix de marché auquel le profit est égal à la perte totale des coûts fixes (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -CF = \pi < 0} ). Si le prix du marché tombe en dessous de ce seuil, les recettes de l'entreprise ne couvrent même pas les coûts variables, et il est donc préférable pour l'entreprise de cesser la production pour minimiser les pertes.
La "Courbe d’offre individuelle à court terme" est la partie de la courbe de coût marginal au-dessus de la courbe de coût variable moyen, indiquant la quantité que l'entreprise est disposée à fournir à différents prix. Si le prix tombe en dessous du seuil de fermeture, l'entreprise a intérêt à cesser son activité, car même les coûts variables ne seraient pas couverts, ce qui mènerait à des pertes supérieures aux coûts fixes seuls.
En résumé, ce graphique démontre comment l'entreprise ajuste sa production en fonction du prix de marché et de ses coûts. Il souligne l'importance du seuil de fermeture comme point de décision critique pour continuer la production à court terme malgré les pertes opérationnelles, avec l'objectif de couvrir au moins les coûts variables et de contribuer aux coûts fixes.
La courbe d’offre de l’entreprise à long terme[modifier | modifier le wikicode]
En économie, l'offre d'une entreprise à long terme est représentée différemment de celle à court terme en raison de la flexibilité qu'a l'entreprise pour ajuster tous ses coûts. À long terme, il n'y a pas de coûts fixes; tous les coûts sont variables, car l'entreprise a suffisamment de temps pour ajuster sa taille et sa capacité de production. Cela signifie que l'entreprise peut entrer ou sortir du marché et ajuster son niveau de production sans être contrainte par des coûts irrécupérables.
La courbe de coût marginal à long terme (CmLT) reflète le coût additionnel de production d'une unité supplémentaire en considérant que l'entreprise peut varier tous ses facteurs de production. La courbe de coût moyen à long terme (CMLT) représente le coût par unité si l'entreprise ajuste sa taille de manière optimale pour chaque niveau de production.
La portion de la courbe de coût marginal de long terme qui se situe au-dessus de la courbe de coût moyen à long terme correspond à la courbe d'offre de l'entreprise à long terme. Cela est dû au fait que, pour maximiser le profit, l'entreprise ne produira et n'offrira des unités supplémentaires sur le marché que si le coût marginal de production de ces unités est inférieur ou égal au prix. Si le coût marginal est supérieur au coût moyen, cela signifie que produire une unité supplémentaire augmenterait le coût moyen, indiquant que l'entreprise n'est pas dans une situation optimale de production.
Ainsi, si le prix de marché est supérieur au coût moyen à long terme, l'entreprise trouvera profitable d'augmenter sa production, car chaque unité supplémentaire vendue apportera un revenu supérieur au coût moyen de production. En revanche, si le prix est inférieur au coût moyen, l'entreprise réduira sa production ou quittera le marché, car elle ne pourrait pas couvrir ses coûts à long terme.
L'offre à long terme d'une entreprise dans un marché parfaitement concurrentiel est donc représentée par la partie ascendante de sa courbe de coût marginal de long terme, à partir du point où elle coupe la courbe de coût moyen de long terme. Cela reflète la capacité et la volonté de l'entreprise de fournir des quantités supplémentaires au marché à un prix qui couvre tous les coûts, incluant un retour sur l'investissement.
Ce graphique dépeint un scénario économique qui décrit les conditions sous lesquelles une entreprise décide de rester active sur le marché ou de s'en retirer à long terme. Il représente les coûts moyens et marginaux de l'entreprise ainsi que les différents prix de marché et leurs implications pour les décisions de l'entreprise.
Nous voyons trois courbes distinctes sur le graphique. La courbe de coût variable moyen (CVM) représente le coût moyen de production excluant les coûts fixes, et elle est la plus basse des trois. La courbe de coût moyen (CM) montre le coût moyen total par unité, y compris les coûts fixes et variables. Cette courbe a une forme en U, suggérant que l'entreprise bénéficie d'économies d'échelle jusqu'à un certain point avant que les déséconomies d'échelle ne prennent effet. La courbe de coût marginal (Cm) indique le coût supplémentaire de production d'une unité supplémentaire et, à long terme, cette courbe est synonyme de l'offre de l'entreprise, mais seulement pour la portion qui se situe au-dessus de la courbe de CM.
La décision de l'entreprise d'entrer ou de sortir du marché dépend du prix de marché par rapport à ces coûts. Lorsque le prix de marché dépasse le coût moyen (comme indiqué par P2 sur le graphique), l'entreprise réalise un profit, car elle est en mesure de couvrir tous ses coûts par unité produite et de générer des revenus supplémentaires. Dans ce cas, l'entreprise a une incitation claire à rester sur le marché.
Si le prix de marché est en dessous du coût moyen mais au-dessus du CVM, comme illustré par P1, l'entreprise opère à perte, car bien qu'elle couvre ses coûts variables, elle ne peut pas couvrir la totalité de ses coûts fixes. Toutefois, si elle anticipe une amélioration future des prix, elle peut décider de rester en activité à court terme, subissant des pertes opérationnelles dans l'espoir de jours meilleurs.
Le seuil de fermeture est le niveau de prix de marché où l'entreprise couvre tout juste ses coûts variables, illustré par la ligne horizontale étiquetée PsF. Si les prix tombent en dessous de ce seuil, la firme décide de quitter le marché car les recettes de vente ne suffiraient même pas à couvrir les coûts variables de production, sans parler des coûts fixes. À ce point, toute production supplémentaire aggraverait les pertes financières de l'entreprise.
Ce graphique illustre l'importance pour les entreprises de surveiller attentivement le marché et de comprendre leur structure de coûts. Les décisions à long terme doivent être prises avec une compréhension claire du point d'équilibre et du seuil de rentabilité pour garantir la viabilité et la durabilité de l'entreprise dans un environnement de marché concurrentiel.
Décision de sortir/entrer[modifier | modifier le wikicode]
La différence entre fermeture et sortie est une distinction cruciale dans la théorie économique, liée aux horizons temporels et à la récupérabilité des coûts. La fermeture est une décision à court terme où l'entreprise cesse la production pour une période donnée, souvent en réponse à des conditions de marché défavorables. Durant cette période, l'entreprise ne génère aucun revenu d'exploitation, mais elle doit toujours faire face à ses coûts fixes (CF), qui sont des coûts irrécouvrables dans le sens où ils ne peuvent pas être récupérés une fois qu'ils ont été payés. Par exemple, les dépenses en capital sur des machines ou des installations, qui ne peuvent pas être vendues ou utilisées pour d'autres fins sans perte significative, sont considérées comme des coûts fixes.
D'autre part, la sortie du marché est une décision à long terme. Elle est prise lorsque l'entreprise prévoit que les conditions de marché ne vont pas s'améliorer suffisamment pour couvrir ses coûts à l'avenir. Dans ce cas, l'entreprise prend en compte tous les coûts, y compris les coûts fixes irrécouvrables, pour décider de cesser définitivement ses opérations. La sortie implique souvent des mesures telles que la vente d'actifs, le licenciement du personnel et la fermeture de sites de production, avec l'intention de ne pas revenir sur le marché.
L'ignorance des coûts fixes lors de la prise de décision de fermeture temporaire est justifiée par le fait que ces coûts seront encourus que l'entreprise produise ou non. Par conséquent, la décision de produire ou de fermer temporairement se base plutôt sur les coûts variables et la capacité de l'entreprise à couvrir ces coûts avec le revenu généré par les ventes. Si le prix de marché ne couvre pas au moins les coûts variables moyens, il est préférable pour l'entreprise de fermer temporairement.
La décision de fermeture temporaire est donc guidée par la viabilité à court terme et la comparaison des revenus avec les coûts variables, tandis que la décision de sortie du marché est une considération à long terme qui prend en compte la totalité des coûts de l'entreprise et les perspectives à long terme de rentabilité sur le marché.
Si une entreprise constate que la recette totale qu'elle obtiendrait de sa production est inférieure à ses coûts totaux à long terme, elle choisira de quitter le marché. Cela est exprimé mathématiquement comme Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RT < CT} . En termes de coûts et de recettes par unité, cette condition peut être reformulée pour indiquer que si le prix de marché (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} ) est inférieur au coût moyen (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CM} ), l'entreprise subira des pertes et ne pourra pas couvrir ses coûts totaux, ce qui justifie la sortie du marché : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p < CM} .
Inversement, si l'entreprise anticipe que la recette totale de sa production dépasserait ses coûts totaux, elle réalisera un profit et sera incitée à entrer sur le marché ou à y rester si elle y est déjà. Mathématiquement, cela signifie que si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RT > CT} , ou à l'unité, que si le prix (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} ) est supérieur au coût moyen (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CM} ), alors l'entreprise peut opérer de manière rentable : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p > CM} .
La courbe d'offre à long terme de l'entreprise reflète la portion de sa courbe de coût marginal qui se trouve au-dessus du coût moyen total. Cela est dû au fait que, à long terme, les entreprises ne resteront sur le marché que si elles peuvent produire à un coût qui leur permet de réaliser un profit, c'est-à-dire lorsque le coût marginal de production d'une unité supplémentaire est égal ou inférieur au prix que l'entreprise peut obtenir sur le marché. À long terme, les entreprises ajustent leur taille et leur capacité de production pour minimiser les coûts et maximiser les profits, ce qui entraîne une offre de marché basée sur le coût marginal par rapport au coût moyen total.
Offre agrégée[modifier | modifier le wikicode]
La courbe d’offre agrégée à court terme[modifier | modifier le wikicode]
La courbe d'offre agrégée sur un marché est créée par l'agrégation des courbes d'offre de toutes les entreprises individuelles qui opèrent sur ce marché. Cette agrégation est faite de manière horizontale, ce qui signifie que pour chaque niveau de prix donné, les quantités offertes par toutes les entreprises sont additionnées pour obtenir la quantité totale offerte sur le marché à ce prix.
Pour clarifier, si nous avons deux entreprises, A et B, et que pour un prix P, l'entreprise A est prête à vendre 10 unités de son produit et l'entreprise B est prête à vendre 15 unités, alors l'offre agrégée à ce prix serait de 25 unités. Si nous traçons ces quantités offertes contre le prix pour toutes les entreprises du marché, nous obtenons la courbe d'offre agrégée.
Cette courbe reflète donc non seulement la réponse de l'offre des entreprises individuelles aux changements de prix, mais aussi l'entrée et la sortie des entreprises du marché, qui peut varier en fonction des conditions économiques et des barrières à l'entrée ou à la sortie. À court terme, l'offre agrégée peut être relativement inélastique, car les entreprises ont des capacités de production et des coûts fixes qui ne peuvent pas être rapidement ajustés. À long terme, cependant, l'offre agrégée peut devenir plus élastique car les entreprises ont le temps d'ajuster leur production et de nouvelles entreprises peuvent entrer sur le marché, augmentant ainsi la quantité totale offerte à chaque niveau de prix.
Avec un nombre fixe d’entreprises (sans sortie ou entrée d’entreprises dans le marché), c’est-à-dire à court terme , on a que :
Dans ces deux graphiques, nous observons la représentation de la courbe d'offre d'une entreprise individuelle et de la courbe d'offre agrégée du marché.
Dans les deux graphiques, nous observons la représentation de la courbe d'offre d'une entreprise individuelle et de la courbe d'offre agrégée du marché.
Le graphique (a) montre la courbe d'offre d'une seule entreprise. La ligne verticale représente le coût marginal (Cm) de production, qui augmente linéairement avec la quantité produite. Cette relation linéaire suggère que chaque unité supplémentaire coûte plus cher à produire que la précédente, ce qui est caractéristique d'une situation où il y a des rendements décroissants à la production. La courbe commence au-dessus de zéro, ce qui indique un coût fixe initial avant la production de toute unité. Le prix auquel l'entreprise est prête à offrir chaque quantité supplémentaire sur le marché est représenté par la hauteur de la courbe de coût marginal.
Le graphique (b) illustre la courbe d'offre agrégée du marché, qui est dérivée de l'addition des quantités fournies par chaque entreprise individuelle à chaque niveau de prix. Cette courbe montre également une relation linéaire entre le prix et la quantité offerte, mais à une échelle beaucoup plus grande. La quantité sur l'axe horizontal est considérablement plus élevée, reflétant l'offre totale de toutes les entreprises sur le marché.
Si nous supposons un nombre fixe d'entreprises sur le marché, c'est-à-dire qu'il n'y a pas d'entrée ou de sortie d'entreprises à court terme, la courbe d'offre du marché n'évoluera pas avec le temps. À court terme, les entreprises ne peuvent ajuster que leur production en réponse aux changements de prix, mais elles ne peuvent pas entrer ou sortir du marché assez rapidement pour affecter la courbe d'offre agrégée. Cela implique que la courbe d'offre agrégée est la somme horizontale des courbes d'offre de toutes les entreprises existantes sur le marché.
Ainsi, à court terme, la courbe d'offre du marché représente la réaction totale de toutes les entreprises existantes aux changements de prix, et elle ne changera que si le prix change ou si les coûts de production des entreprises existantes changent. Toute augmentation du nombre d'entreprises ou changements dans la technologie de production, qui pourraient affecter les coûts marginaux, ne seront reflétés dans la courbe d'offre qu'à long terme.
La courbe d’offre agrégée à long terme[modifier | modifier le wikicode]
Dans un marché concurrentiel à long terme, les entreprises ajustent leur niveau de production et les nouvelles entreprises décident d'entrer ou de sortir du marché en fonction des profits économiques réalisés. Ces ajustements sont influencés par la relation entre le prix du marché (P) et le coût moyen (CM) des entreprises.
Si le prix du marché est supérieur au coût moyen, cela indique que les entreprises présentes sur le marché réalisent des profits économiques positifs. Cette situation est attractive pour les nouvelles entreprises, qui choisiront d'entrer sur le marché pour bénéficier de ces profits. L'entrée de nouvelles entreprises accroît la quantité offerte sur le marché, ce qui, selon les lois de l'offre et de la demande, conduit à une baisse du prix du marché. La courbe d'offre agrégée se déplace alors vers la droite. Ce processus se poursuit jusqu'à ce que le prix du marché soit égal au coût moyen, ce qui élimine les profits économiques et rétablit un équilibre.
Inversement, si le prix du marché est inférieur au coût moyen, les entreprises existantes subissent des pertes, ce qui signifie qu'elles font des profits économiques négatifs. Dans cette situation, certaines entreprises choisiront de sortir du marché, ce qui réduit l'offre totale. La diminution de l'offre entraîne une hausse du prix du marché jusqu'à ce qu'il atteigne le niveau du coût moyen.
À l'équilibre de long terme, le prix du marché sera égal au coût moyen, et donc, les profits économiques seront nuls. À ce point, il n'y a ni incitation à l'entrée ni à la sortie du marché pour les entreprises, et la courbe d'offre agrégée devient parfaitement élastique ou horizontale. Cela signifie que les entreprises peuvent vendre n'importe quelle quantité de leur produit au prix du marché sans influencer ce prix. Cet équilibre est caractéristique d'une concurrence parfaite où le libre jeu du marché conduit à une efficacité allocative, avec les entreprises produisant à leur niveau le plus efficient.
Le raisonnement à la marge reste fondamental dans la détermination de la production optimale pour une entreprise individuelle, car il indique que l'équilibre de maximisation des profits est atteint lorsque le prix du marché (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} ) est égal au coût marginal (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Cm} ). Cette condition s'applique à chaque entreprise et dicte la quantité qu'elle offre sur le marché pour maximiser ses profits.
Dans un marché concurrentiel à long terme, cependant, la dynamique change. Si des entreprises réalisent des profits économiques positifs (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p > CM} ), cela attire de nouvelles entreprises sur le marché, augmentant l'offre totale et poussant les prix vers le bas jusqu'à atteindre le niveau du coût moyen (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p = CM} ). Inversement, si des entreprises subissent des pertes (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p < CM} ), certaines quitteront le marché, réduisant l'offre et faisant augmenter les prix jusqu'à ce qu'ils égalisent à nouveau le coût moyen. Ce processus d'entrée et de sortie se poursuit jusqu'à ce que les profits économiques soient nuls, menant à une situation où Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p = CM} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p = Cm} .
À ce stade d'équilibre à long terme, les entreprises opèrent là où le coût moyen et le coût marginal sont minimaux et égaux au prix du marché. Cela correspond à la production au point d'efficacité productive minimale ou à l'efficience des échelles minimales (EME), où Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle CM} est au plus bas. La courbe d'offre agrégée à long terme est alors horizontale ou parfaitement élastique à ce niveau de prix, indiquant que le marché peut absorber n'importe quelle quantité au prix où les coûts moyens sont minimisés. Aucune entreprise n'a la capacité ou l'incitation à modifier ce prix, car toutes font un profit nul et n'ont donc pas de profits économiques à maximiser. En résumé, le marché à long terme s'ajuste de sorte que Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p = CM} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p = Cm} , et la courbe d'offre du marché est parfaitement horizontale au prix correspondant à l'EME.
Profits économiques nuls : intuition[modifier | modifier le wikicode]
Il est essentiel de distinguer entre profit économique et profit comptable, notamment lorsqu'on analyse les conditions d'équilibre d'une entreprise sur le marché à long terme. Un profit économique nul ne signifie pas que les propriétaires d'une entreprise ne tirent aucun revenu de leur investissement. En réalité, cela indique que l'entreprise génère juste assez de revenus pour couvrir tous ses coûts, y compris les coûts d'opportunité associés à l'investissement de capital et au temps des propriétaires.
Le coût d'opportunité est la valeur de la meilleure alternative à laquelle on renonce lorsqu'on fait un choix. Dans le contexte d'une entreprise, cela inclut les revenus que les propriétaires pourraient obtenir s'ils investissaient leur temps et leur argent ailleurs. Ainsi, à l'équilibre de profit nul, l'entreprise compense ses propriétaires pour ces coûts d'opportunité, ce qui signifie qu'ils reçoivent le retour qu'ils auraient pu espérer de leur second meilleur investissement ou emploi de leur temps et de leur argent.
En termes comptables, les profits peuvent apparaître comme positifs. Cela est dû au fait que le profit comptable est calculé en soustrayant les coûts explicites des revenus totaux, sans prendre en compte les coûts implicites ou d'opportunité. Par conséquent, une entreprise peut afficher un profit comptable tout en ayant un profit économique nul. Le profit économique est une mesure plus complète de la rentabilité, car il inclut à la fois les coûts explicites et implicites.
Dans un marché parfaitement concurrentiel à long terme, les profits économiques nuls sont la norme, car les forces du marché érodent les profits économiques positifs par l'entrée de nouvelles entreprises, et les profits économiques négatifs par la sortie des entreprises existantes. Ce processus se poursuit jusqu'à ce que toutes les entreprises sur le marché ne réalisent plus que des profits économiques nuls, assurant ainsi que les ressources sont allouées de la manière la plus efficace possible, c'est-à-dire là où elles sont les plus valorisées.
Courbe d’offre de long terme croissante[modifier | modifier le wikicode]
La courbe d'offre à long terme peut présenter une pente positive dans certaines situations, même dans le cadre de la concurrence parfaite. La pente positive de la courbe d'offre à long terme reflète l'idée que, bien que les entreprises puissent entrer et sortir librement du marché, toutes les entreprises ne sont pas identiques, et les ressources qu'elles utilisent ne sont pas parfaitement substituables et peuvent être limitées.
Un facteur clé de cette dynamique est la disponibilité limitée de certaines ressources ou facteurs de production. Prenons l'exemple de la terre agricole : elle est disponible en quantité limitée et toutes les parcelles de terre ne sont pas également fertiles. Au fur et à mesure que la production agricole s'accroît, les nouvelles entreprises peuvent être forcées d'utiliser des terres moins productives ou plus coûteuses à cultiver, ce qui augmente leur coût moyen de production.
À mesure que de nouvelles entreprises entrent sur le marché en réponse à des profits économiques positifs, elles font face à des coûts plus élevés que les entreprises déjà établies. Cela signifie que même si le prix du marché est suffisant pour couvrir les coûts des entreprises existantes, il ne peut pas être suffisant pour les nouvelles entreprises avec des coûts plus élevés. En conséquence, l'entreprise marginale - celle qui est indifférente entre entrer sur le marché ou non en raison de ses coûts plus élevés - détermine le prix du marché à l'équilibre.
La condition de profit nul s'applique donc à cette entreprise marginale et non à toutes les entreprises du marché. Les entreprises plus établies ou plus efficaces réaliseront des profits économiques, mais l'entrée de nouvelles entreprises avec des coûts plus élevés se poursuivra jusqu'à ce que les prix baissent suffisamment pour éliminer ces profits économiques pour l'entreprise marginale.
La courbe d'offre à long terme avec une pente positive est donc le résultat de l'entrée de nouvelles entreprises avec des fonctions de coût progressivement plus élevées, et elle reste plus élastique que la courbe d'offre à court terme. Cela est dû au fait qu'à court terme, les entreprises ne peuvent pas ajuster leur taille ou leur structure de coûts, et donc l'offre est moins sensible aux changements de prix. À long terme, avec la possibilité d'ajuster la production et l'entrée et la sortie de nouvelles entreprises, la courbe d'offre peut devenir plus réactive aux changements de prix, même si elle présente une pente positive.
Mécanisme d’ajustement : court versus long terme[modifier | modifier le wikicode]
Situation initiale[modifier | modifier le wikicode]
Les deux graphiques suivants illustrent la dynamique de l'offre et de la demande dans une situation initiale à court et à long terme pour une entreprise et pour un marché.
Dans le premier graphique, dédié à une entreprise individuelle, nous voyons deux courbes: la courbe de coût moyen (CM) et la courbe de coût marginal (Cm). La courbe de coût marginal croise la courbe de coût moyen à son point le plus bas, ce qui est typique car cela indique le niveau de production le plus efficace pour l'entreprise. Le prix de marché (P1) est indiqué et il semble être égal au coût marginal et au coût moyen, ce qui signifierait que l'entreprise fait ni profit ni perte; elle couvre juste ses coûts.
Le deuxième graphique montre l'offre et la demande sur le marché global. L'offre à court terme (S1) est représentée par une courbe ascendante, indiquant que plus le prix est élevé, plus les entreprises sont disposées à offrir de produits. La courbe d'offre à long terme est représentée comme une ligne horizontale, ce qui indique que le marché peut absorber toute quantité au prix P1 sans que cela affecte le prix, reflétant une situation d'équilibre à long terme où les entreprises ne font que couvrir leurs coûts. La demande (D1) croise l'offre à court terme au point A, définissant la quantité de marché initiale (q1) et le prix P1.
L'analyse des graphiques montre un mécanisme d'ajustement de marché:
- À court terme : Si le prix de marché est au-dessus du coût moyen, les entreprises existantes réaliseront des profits, incitant à une augmentation de l'offre. Si le prix est en dessous du coût moyen, les entreprises subiront des pertes, menant à une réduction de l'offre. La courbe de coût marginal indique la quantité que l'entreprise est prête à fournir à différents prix.
- À long terme : La courbe d'offre à long terme est parfaitement élastique au prix P1, ce qui suggère que le marché est en équilibre et que toutes les entreprises opèrent à un niveau où le coût moyen est égal au prix de marché. À ce stade, aucune nouvelle entreprise n'a d'incitation à entrer sur le marché, et aucune entreprise n'a d'incitation à sortir, car toutes couvrent leurs coûts, y compris un retour normal sur le capital (représenté par le coût moyen).
Le mécanisme d'ajustement entre court et long terme est donc caractérisé par des entrées et sorties d'entreprises du marché jusqu'à ce que le profit économique soit nul, et que le prix se stabilise au niveau où les entreprises couvrent tous leurs coûts, y compris le coût d'opportunité du capital et du travail. Cela entraîne une offre de marché plus élastique à long terme par rapport à court terme, où la quantité produite peut fluctuer plus largement en réponse aux changements de prix sans que cela affecte le prix lui-même.
Choc exogène positif de demande[modifier | modifier le wikicode]
Ces deux graphiques illustrent la réaction à court terme d'une entreprise et d'un marché global à un choc exogène positif de la demande, entraînant une augmentation du prix.
Dans le graphique de l'entreprise, nous voyons que le nouveau prix du marché (P2) est supérieur au coût moyen (CM) et au coût marginal (Cm). Cela indique que l'entreprise est maintenant en mesure de réaliser un profit, représenté par la zone colorée entre le prix P2 et les courbes de coût. La différence entre le prix de vente et le coût moyen par unité sur la quantité produite représente le profit par unité. La réponse immédiate de l'entreprise à ce prix plus élevé sera d'augmenter la production pour maximiser ses profits, car chaque unité supplémentaire vendue au-dessus du coût marginal contribue au profit total.
Sur le graphique du marché, la demande initiale (D1) croise l'offre à court terme (S1) au point A, établissant la quantité de marché initiale (q1) et le prix P1. Après le choc de la demande, la nouvelle courbe de demande (D2) se déplace vers la droite, indiquant que pour chaque prix, les consommateurs sont désormais prêts à acheter plus de biens. La nouvelle intersection de la demande avec l'offre à court terme se trouve au point B, où la quantité de marché a augmenté à q2 et le prix a augmenté à P2.
Cette hausse du prix à court terme, de P1 à P2, reflète la réponse immédiate du marché à l'accroissement de la demande. Le prix plus élevé entraîne des profits économiques positifs pour les entreprises (P2 > CM), illustrés par le profit sur le graphique de l'entreprise. Cependant, cette situation est temporaire à court terme. À long terme, ces profits économiques positifs (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi > 0} ) attireront de nouvelles entreprises sur le marché, augmentant l'offre et exerçant une pression à la baisse sur les prix. En conséquence, la courbe d'offre à long terme devrait s'ajuster vers la droite jusqu'à ce que le prix revienne au niveau où les profits économiques sont nuls (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p = CM} ), rétablissant ainsi l'équilibre à long terme où les entreprises ne gagnent qu'un retour normal sur leur investissement.
En bref, à court terme, l'entreprise peut profiter de prix plus élevés et de profits accrus. Cependant, la dynamique à long terme du marché, influencée par la libre entrée et sortie des entreprises, tend à éroder ces profits et à ramener le marché à un nouvel équilibre où les profits économiques sont nuls et le prix correspond au coût moyen de toutes les entreprises.
Le profit économique de court terme attire des nouvelles entreprises dans le marché[modifier | modifier le wikicode]
Ces deux graphiques qui illustrent la réponse de long terme d'une entreprise et d'un marché à un choc de demande positif.
Le premier graphique montre la situation d'une entreprise individuelle. On y voit que le coût marginal (Cm) et le coût moyen (CM) restent inchangés par rapport à la situation initiale, indiquant que les coûts de production n'ont pas changé à long terme. Le prix sur le marché pour l'entreprise est de retour à P1, ce qui suggère que les profits à court terme qui étaient présents à cause du prix élevé P2 ont été érodés par l'entrée de nouvelles entreprises sur le marché.
Le second graphique illustre la situation sur le marché dans son ensemble. À la suite du choc de demande initial qui a déplacé la courbe de demande de D1 à D2, le prix a augmenté de P1 à P2 et la quantité de marché de q1 à q2. En réponse à ces profits économiques temporaires, de nouvelles entreprises sont entrées sur le marché, ce qui a déplacé l'offre de court terme de S1 à S2. L'accroissement de l'offre a exercé une pression à la baisse sur les prix, conduisant à un nouveau point d'équilibre à long terme au point C, où le prix est redescendu à P1 et la quantité a augmenté à q3.
À long terme, la courbe d'offre s'est déplacée vers la droite de S1 à S2 en raison de l'entrée de nouvelles entreprises, qui ont été attirées sur le marché par les profits économiques réalisés lorsque les prix étaient à P2. L'ajustement de l'offre continue jusqu'à ce que le prix sur le marché revienne au niveau où les entreprises ne font que couvrir leurs coûts, éliminant ainsi les profits économiques et ramenant le prix au niveau du coût moyen. À ce stade, le marché est de retour à un état d'équilibre où les entreprises existantes et nouvelles opèrent sans réaliser de profit économique (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi = 0} ), car le prix est égal au coût moyen (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p = CM} ), ce qui est caractéristique de la concurrence parfaite à long terme.
L'offre de long terme dans le graphique du marché reste horizontale, indiquant que le marché à long terme peut toujours absorber des quantités supplémentaires au prix d'équilibre sans que cela n'entraîne de variation de prix. Cela reflète une condition d'entrée libre et parfaite sur le marché et l'ajustement des entreprises aux conditions de marché de sorte que seul un retour normal sur investissement est réalisé.
Résumé[modifier | modifier le wikicode]
Dans un marché compétitif, le revenu total d'une entreprise est directement lié au volume de sa production, car elle est considérée comme un "preneur de prix" — c'est-à-dire qu'elle n'a pas la capacité d'influencer le prix du marché par ses propres actions. Le prix auquel elle vend son produit est à la fois son revenu moyen par unité vendue et son revenu marginal pour la dernière unité vendue. Pour maximiser ses profits, l'entreprise ajuste sa production jusqu'à ce que son coût marginal égale ce prix de marché donné. Ainsi, la courbe de coût marginal de l'entreprise correspond à sa courbe d'offre à court terme.
À court terme, une entreprise peut se retrouver dans une situation où elle ne peut pas couvrir ses coûts fixes en raison de contraintes opérationnelles ou contractuelles. Si le prix de marché tombe en dessous du coût variable moyen, cela signifie que l'entreprise ne peut même pas couvrir ses coûts variables en produisant. Dans ce cas, il serait plus rationnel pour l'entreprise de cesser temporairement sa production plutôt que de continuer à opérer à perte.
À long terme, cependant, une entreprise a la flexibilité de modifier sa structure de coûts et sa capacité de production. Les coûts fixes deviennent variables, car ils peuvent être ajustés grâce à des décisions d'investissement ou de désinvestissement. Une entreprise décidera de quitter le marché si le prix est inférieur au coût moyen, ce qui signifie qu'elle ne peut pas réaliser de profit, même en couvrant tous ses coûts variables et fixes.
Lorsque l'entrée et la sortie des entreprises sur le marché sont libres et sans obstacle, on atteint un équilibre à long terme où les profits économiques des entreprises sont nuls, et les entreprises opèrent à leur efficacité minimale des échelles (EME), qui est le point où le coût moyen est à son minimum. Cependant, si les fonctions de coût varient d'une entreprise à l'autre en raison de différences dans l'efficacité, l'accès aux technologies, la qualité des intrants, ou d'autres facteurs, certaines entreprises peuvent réaliser des profits positifs même à long terme, tandis que d'autres pourraient opérer à l'équilibre ou même subir des pertes.
Cet état reflète un marché en parfait équilibre, où le prix permet juste de couvrir le coût de production de l'entreprise la moins efficace qui reste sur le marché. Les entreprises plus efficaces que cette dernière peuvent réaliser des profits économiques, tandis que les moins efficaces ne peuvent pas survivre et quittent le marché.