Vote et Choix Social
Choix social[modifier | modifier le wikicode]
La question fondamentale est de savoir comment agréger les préférences individuelles en une décision collective ? Vote ? Marché ? Ici, nous allons introduire le problème, nous allons étudier brièvement quelques propriétés de chaque système (et leurs limites).
Agréger les préférences[modifier | modifier le wikicode]
Le problème est que parfois il n’est pas possible de sélectionner une alternative avec le vote majoritaire (Cycle de Condorcet). Il y a un débat historique pour résoudre ces problèmes entre Condorcet et Borda.
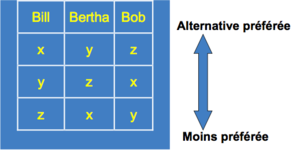
Vote majoritaire[modifier | modifier le wikicode]
- x bat y
- y bat z
- z bat x
Pas d’alternative sélectionnée !
Les préférences individuelles, transitives, ne sont pas agrégées en une préférence collective transitive.
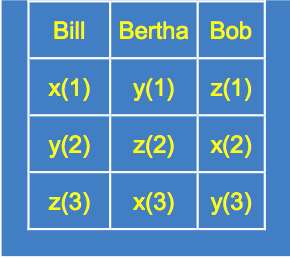
Vote Pondéré[modifier | modifier le wikicode]
- x-score = 6
- y-score = 6
- z-score = 6
Aucun candidat n’est sélectionné.
Considérations stratégiques[modifier | modifier le wikicode]
En plus de ces problèmes, la plupart des systèmes de vote sont sensibles à la manipulation stratégique.
Un individu peut voter différemment de ses préférences afin d’obtenir le résultat qui l’arrange le plus.
Par exemple, le vote pondéré.
Introduisons une nouvelle alternative (candidat).
- x-score = 8
- y-score = 7
- z-score = 6
- α-score = 9
z gagne !
Propriétés désirables d’un système de vote[modifier | modifier le wikicode]
- Doit amener à des préférences sociales complètes, réflexives and transitives (comme les préférences individuelles).
- Unanimité : si tous les individus préfèrent à , alors ce doit être le cas du système de vote.
- Les préférences sociales entre et doivent seulement dépendre des préférences individuelles entre et .
Théorème d’impossibilité de Arrow : La seule règle de vote qui remplit ces trois conditions est la règle dictatoriale !
Si nous voulons adopter une règle non- dictatoriale il nous faut donc abandonner une propriété désirable...
Laquelle des procédures abandonner ? La 3 car il existe beaucoup de procédures remplissant les propriétés 1 et 2.
Plusieurs méthodes en économie[modifier | modifier le wikicode]
est l’utilité de l’individu quand l’alternative est sélectionnée.
- Utilitariste :
- Pondéré :
- Minimax :
Problèmes de ces méthodes basées sur l’utilité ?
Utilité : fonction qui représente les préférences. Le choix d’une fonction particulière est arbitraire.
Fonction de bien être social[modifier | modifier le wikicode]
Supposons que le bien être de chaque individu dépende seulement de sa propre allocation.
Utilité individuelle est , plutôt que .
Alors la fonction de bien être social, , est : où est une fonction croissante.
Efficacité[modifier | modifier le wikicode]
Toute allocation sociale optimale doit être Pareto-Efficace.
Sinon on pourrait augmenter l’utilité d’un agent sans diminuer celle d’un autre, signifiant que l’allocation initiale n’était pas optimale.
Efficacité : deux agents[modifier | modifier le wikicode]
Allocations Equitables[modifier | modifier le wikicode]
Plusieurs allocations Pareto-Efficace sont “injustes”.
Par exemple : un individu consomme toute la ressource. Est-ce efficace ? Est-ce Juste ?
Besoin d’une définition de “juste” dans notre contexte.
Si l’agent A préfère l’allocation de l’agent B à la sienne, alors on dit que l’agent A envie l’agent B.
Une allocation est Juste si elle est :
- Pareto efficace (pourquoi ?).
- Ne crée pas d’envie.
Est-ce que l’égalité des allocations entraîne forcément des allocation Justes ?
3 agents, même allocation.
- Les agents A et B ont les mêmes préférences. Pas l’agent C.
- Agents B et C échangent ⇒ agent B atteint une satisfaction supérieure.
- Donc, l’agent A envie l’agent B ⇒ l’allocation est “injuste”.
Par contre si les échanges se font sur un marché compétitif, alors une allocation initiale égalitaire entrainera toujours une allocation finale juste.
2 agents, même allocation initiale.
- Allocations initiales : Échec de l’analyse (erreur de syntaxe): {\displaystyle (ω_1,ω_2)} .
- Après l’échange : et
- Soit, Échec de l’analyse (erreur de syntaxe): {\displaystyle p_1x_1^A + p_2x_2^A = p_1ω_1 + p_2ω_2} et Échec de l’analyse (erreur de syntaxe): {\displaystyle p_1x_1^B + p_2x_2^B = p_1ω_1 + p_2ω_2} .
Supposons que A envie B.
- I.e.
- Alors, pour l’agent A, Échec de l’analyse (erreur de syntaxe): {\displaystyle p_1x_1^B + p_2x_2^B > p_1x_1^A + p_2x_2^A = p_1ω_1 + p_2ω_2} .
Contradiction !
Premier théorème du bien être[modifier | modifier le wikicode]
Etant donné des préférences normales, échanger sur un marché compétitif implémente une allocation Pareto-Optimale.
Deuxième théorème du bien être[modifier | modifier le wikicode]
Ce théorème est suivi par un deuxième théorème, montrant que l’efficacité et les considérations redistributives peuvent être séparées.
L’idée est que toutes les allocations sur la courbe de contrats peuvent être atteintes par une allocation initiale spécifique et en laissant un échange de marché s’opérer.
Etant donné des préférences normales, il est toujours possible d’atteindre une allocation Pareto-Optimale donnée en sélectionnant un vecteur de prix et des dotations initiales spécifiques et en laissant l’échange compétitif s’effectuer.