Théorie des jeux
La théorie des jeux est une approche visant à modéliser les comportements stratégiques des agents (individus, firmes, pays...).
Les agents prennent en compte la stratégie des autres pour définir leur plan d’actions.
Environnement ou les actions des agents ont un impact sur le gain des autres.
Applications[modifier | modifier le wikicode]
Oligopoles, cartels (OPEC)...
Externalités, bien public, ressources naturelles (tragédie des communs).
Théorie des contrats, processus de négociation.
Négociations internationales, conflits...
Un jeu ?[modifier | modifier le wikicode]
Un jeu consiste en,
- Un ensemble de joueurs,
- Un ensemble de stratégies pour chaque joueur,
- Un ensemble de gains pour chaque joueur, spécifiés pour chaque stratégie des autres joueurs.
Dans cette séance: seulement des jeux à deux joueurs, avec deux actions chacun.
NB: Une stratégie est un ensemble d’actions, contingente aux actions des autres joueurs.
Une Stratégie[modifier | modifier le wikicode]
Intuition: pour chaque action de l’autre joueur, elle spécifie l’action à prendre. Vous pourriez écrire une stratégie afin qu’un ami joue pour vous.
Concept de “Meilleure réponse” : meilleure action possible, étant donné l’action jouée par l’autre joueur.
2 joueurs[modifier | modifier le wikicode]
2 joueurs : 1 et 2.
- Joueur 1 : actions possibles, “Haut” et “Bas”.
- Joueur 2 : actions possibles,“Gauche” et “Droite”.
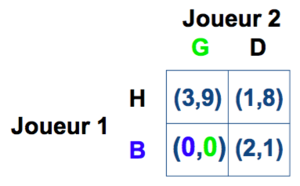
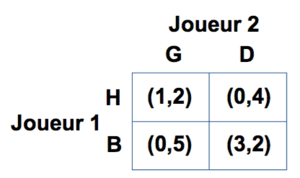
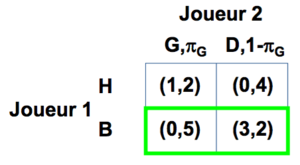
La table qui montre les gains de chaque joueur en fonction des actions jouées est appelée matrice des gains.
Les gains de 1 sont en premier dans la parenthèse, les gains de 2 sont en deuxième. Les joueurs jouent simultanément.
E.g. 1 joue “Haut” et 2 joue “Droit”: gain de 1 est 1 et gain de 2 est 8.
Quels types de résultats sont les plus probables ?
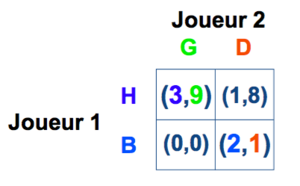
Si 2 joue “D” quelle est la meilleure réponse de 1 ?
(B,D) est crédible ?
Si 2 joue “D” quelle est la meilleure réponse de 1 ?
Si 1 joue “B” quelle est la meilleure réponse de 2 ?
Si 1 joue “H” quelle est la meilleure réponse de 2 ?
Si 2 joue “G” quelle est la meilleure réponse de 1 ?
(H,B) ?
Équilibre de Nash[modifier | modifier le wikicode]
Quand les stratégies sont des meilleures réponses les unes aux autres, on parle d’équilibre de Nash.
A un équilibre de Nash, un joueur obtient un gain maximal étant donné la stratégie de l’autre joueur.
Autre façon de l’interpréter: à un équilibre de Nash, aucun joueur ne veut changer d’action, étant donné la stratégie de l’autre joueur.
Notre exemple a deux équilibres de Nash; (H,G) et (B,D).
L’équilibre (3,9) va-t-il être plus joué car préféré par les 2 joueurs ?
Dilemme du prisonnier[modifier | modifier le wikicode]
Jeu emblématique de la théorie. Permet d’illustrer que les situations Pareto-Optimale ne sont pas toujours naturellement choisies.
Bonnie et Clyde sont arrêtés par la police à bord d’une voiture volée. Un cadavre est dans le coffre. La police a des preuves suffisantes pour les inculper du vol de voiture, mais pas du meurtre : il faut un aveu.
Le sheriff interroge B et C séparément et leur propose un deal sur leurs peines respectives.
Si Bonnie joue “Silence”, qu’elle est la meilleure réponse de Clyde ?
Si Bonnie joue “Confession” qu’elle est la meilleure réponse de Clyde ?
Quoi que joue Bonnie, Clyde va toujours jouer “confession”.
Confesser est une stratégie dominante pour Clyde. De même pour Bonnie.
Le seul éq. de Nash du jeu: (C,C). Est-il efficace ? Conclusion ?
Une stratégie dominante est une stratégie qui apporte le gain maximal à un joueur, quel que soit la stratégie utilisée par les autres joueurs.
Un équilibre en Stratégie Dominante: quand chaque joueur utilise une stratégie dominante.
Concept d’équilibre plus fort que l’équilibre de Nash (eq. en strat dom. est toujours un eq. de Nash, l’inverse n’est pas vrai).
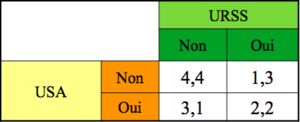
Course aux armements[modifier | modifier le wikicode]
Pur problème de coordination.
N.B. ≠ du dilemme du prisonnier : ici deux équilibres – (Non, Non) et (Oui, Oui) – dont un Pareto supérieur.
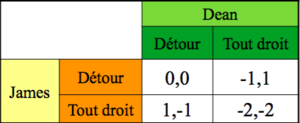
Jeu de la poule mouillée[modifier | modifier le wikicode]
Conflit pur.
Solutions : engagement (on bloque le volant) ou jeux répétés (réputation)
N.B. deux équilibres – (Tout droit, Détour) et (Détour, Tout droit) – dont aucun n’est Pareto supérieur.
Séquence[modifier | modifier le wikicode]
Jusqu’à présent les joueurs jouaient simultanément.
Jeux simultanés.
Mais ils existe beaucoup de situation où les agents jouent en séquence.
=> Jeux séquentiels (ici à deux joueurs).
Le premier joueur est appelé le meneur, celui qui joue second est dénommé suiveur.
Exemple précédent : (H,G) et (B,D) sont chacun des éq. de Nash du jeu simultané.
Supposons désormais que le jeu devienne séquentiel.1 joue premier, 2 second.
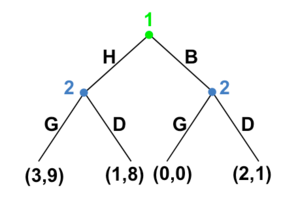
Nous pouvons réecrire le jeu dans sa forme étendue.
1 joue premier. 2 second.
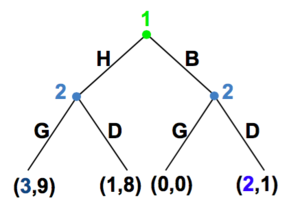
(H,G) est un equilibre de Nash.
(B,D) est aussi un équilibre de Nash. La séquentalité nous permet-elle de “sélectionner “un eq. ?
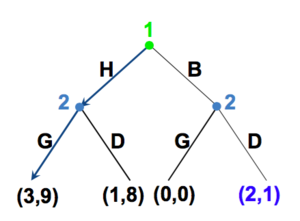
Si 1 joue H, alors 2 joue G; 1 obtient 3.
- Si 1 joue H, alors 2 joue G; 1 obtient 3.
- Si 1 joue B, alors 2 joue D; A obtient 2.
(H,G) est le seul éq. en sous-jeu.
Stratégies Pures[modifier | modifier le wikicode]
2 eq. de Nash: (H,G) and (B,D).Une stratégie pure est une stratégie mixte sans probabilité. wsh
Un nouveau jeu. Existe-t-il un éq. en stratégies pures ?
Le jeu n’a pas d’éq. en stratégie pure. Cependant nous pouvons regarder les stratégies mixtes.
Stratégies Mixtes[modifier | modifier le wikicode]
Plutôt que de choisir une action “Haut” ou “Bas”, un joueur sélectionne des probabilités distribuées sur ces actions ().
Avec une proba. 1 va jouer “Haut” et avec une proba. il va jouer “Bas” (i.e. jette une pièce pour 50/50).
Le joueur 1 “mixe” sur les stratégies pures.
La distribution de proba. () est une stratégie mixte pour le joueur 1.
Comment trouve-t-on un éq. en stratégie mixte ?
Si 2 joue “Gauche” son gain espéré est
- 2 joue “gauche” : .
- 2 joue “droite” : .
Si 2 ne jouerait que “gauche”.
Mais on sait qu’il n’y a pas d’eq. de Nash dans lequel 2 joue toujours “gauche”. De même pour “droite”.
Donc, pour qu’un eq. existe il faut que 2 soit indifférent entre les deux actions : =>
- 1 joue “Haut”, gain espéré :
- 1 joue “Bas”, gain espéré :
Si 1 jouerait toujours “haut”. Mais on sait qu’il n’existe aucun eq. dans lequel 1 joue toujours “Haut”. De même pour “bas”.
Donc, pour qu’un eq. existe il faut que 2 soit indifférent entre les deux actions : ⇒ .
Le seul éq. de Nash du jeu est en stratégies mixtes, avec 1 qui joue (3/5, 2/5) et 2 qui joue (3/4, 1/4).
Les gains vont être (1,2) avec une proba de :
Le gain espéré de 1 à cet équilibre :
Le gain espéré de 2 à cet équilibre :
Exemple[modifier | modifier le wikicode]
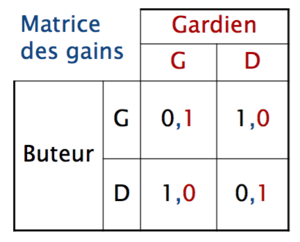
Exemple du jeu des tirs au but
- 2 joueurs : Gardien et buteur
- 2 stratégies : tirer/plonger à gauche/droite
- Hypothèse de « talent » des joueurs
- Le buteur ne tire jamais à coté
- Le gardien intercepte toujours si du bon coté
Quelle est la matrice des gains ?
Il existe cependant un équilibre en stratégies mixtes
Stratégie pour les 2 joueurs:
- Jouer G et D 50%du temps (1 fois sur deux).
- Chaque cas à une probabilité de 0.25.
- Le buteur marque un but sur deux, l’autre est arrêté par le gardien.
Stratégies pures, stratégies mixtes[modifier | modifier le wikicode]
Vérifions que cet équilibre est bien un équilibre de Nash :
Le gardien joue G et D 50% du temps. Le buteur peut il augmenter son taux de succès en déviant de la règle 50- 50?
Si le buteur décide de jouer 60% à gauche et 40% à droite, son taux de succès est :
En choisissant 60-40, le buteur marque plus à gauche mais moins à droite. Son taux de succès est le même, il ne peut donc pas améliorer sa situation.
Existence d’équilibre[modifier | modifier le wikicode]
Résultat de Nash (années 1950): un jeu avec un nombre de joueurs fini, chacun avec un nombre de stratégie finie, possède au moins un équilibre.
Si un jeu n’a pas d’équilibre en stratégie pure, il doit avoir un équilibre en stratégies mixtes.
Annexes[modifier | modifier le wikicode]
- Universalis, Encyclopædia. “ÉQUILIBRE ÉCONOMIQUE.” Encyclopædia Universalis, https://www.universalis.fr/encyclopedie/equilibre-economique/10-l-equilibre-de-nash/.
- Hernandez, Julien. “Coopérer Ou Trahir? LA COMPLEXE RECETTE De La Confiance.” LE FIGARO, 2021, https://www.lefigaro.fr/sciences/cooperer-ou-trahir-la-complexe-recette-de-la-confiance-20210411.