Le Choix
La rationalité économique
[modifier | modifier le wikicode]L'hypothèse comportementale de la rationalité nous permet d'affirmer que le consommateur va sélectionner la meilleure alternative possible qui s'offre à lui.
Démarche : Le consommateur doit faire un choix sous contrainte.
Il va sélectionner l’alternative qui lui apporte la plus grande satisfaction étant donné ses contraintes.
Formellement : maximisation de la fonction d'utilité sous la contrainte de budget.
L'ensemble des choix possibles (respectant la contrainte de budget) est l'ensemble des choix.
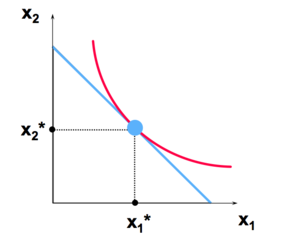
Où se situe le meilleur choix possible sur le graphique usuel à deux biens ?
Choix rationnel contraint
[modifier | modifier le wikicode]
Le Choix optimal
[modifier | modifier le wikicode]($ x_{1}^{*},x_{2}^{*} $) est le panier préféré parmi ceux que l'agent peut s'offrir.
Choix optimal
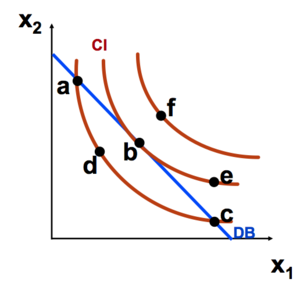
[modifier | modifier le wikicode]Confrontation entre préférences et possibilités
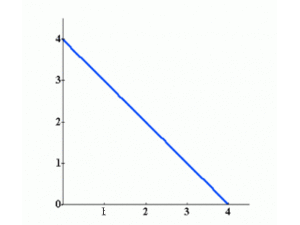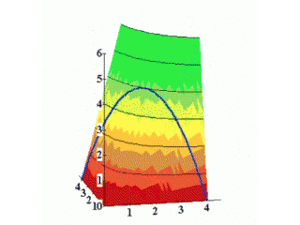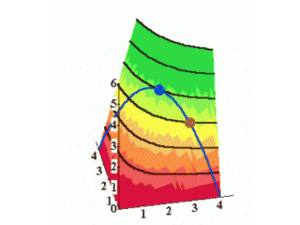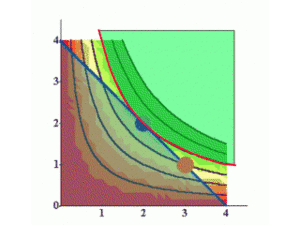
Pourquoi le panier b domine-t-il tous les autres ?
Le panier préféré pour un agent, étant donné les prix et le revenu, est dénoté par ($ x_{1}^{*},x_{2}^{*} $).
Il se trouve sur la courbe d’indifférence la plus haute possible, tout en étant sur la contrainte budgétaire
Nous allons utiliser ces propriétés pour le déterminer formellement.
($ x_{1}^{*},x_{2}^{*} $) satisfait 2 conditions:
- (a) tout le budget est dépensé; $ p_{1}x_{1}^{*}+p_{2}x_{2}^{*}=m $
- (b) La pente de la droite de budget, $ -{\frac {p_{1}}{p_{2}}} $, et la pente de la CI contenant ($ x_{1}^{*},x_{2}^{*} $) sont égales à ($ x_{1}^{*},x_{2}^{*} $).
Cette information va nous permettre de trouver le panier optimal, étant donné des préférences (une fonction d'utilité), des prix et le revenu.
Exemple
[modifier | modifier le wikicode]Supposons les préférences suivantes :
- $ U(x_{1},x_{2})=x_{1}^{a}x_{2}^{b} $
Alors :
- $ UM_{1}={\frac {\partial U}{\partial x_{1}}}={\frac {1}{2}}x_{1}^{-{\frac {1}{2}}}x_{2}^{\frac {1}{2}} $
- $ UM_{2}={\frac {\partial U}{\partial x_{2}}}={\frac {1}{2}}x_{1}^{\frac {1}{2}}x_{2}^{-{\frac {1}{2}}} $
Utilité Cobb-Douglas
[modifier | modifier le wikicode]Le TMS est égal à :
- $ TMS={\frac {dx_{2}}{dx_{1}}}=-{\frac {\frac {\partial U}{\partial x_{1}}}{\frac {\partial U}{\partial x_{2}}}}=-{\frac {ax_{1}^{a-1}x_{2}^{b}}{bx_{1}^{a}x_{2}^{b-1}}}=-{\frac {ax_{2}}{bx_{1}}} $
À ($ x_{1}^{*},x_{2}^{*} $), $ TMS=-{\frac {p_{1}}{p_{2}}} $ soit :
- Échec de l’analyse (erreur de syntaxe): - \frac {ax_2}{bx_1} = - \frac {p_1}{p_2} ⇒ x_2^* = \frac {bp_1}{ap_2} x_1^* (A)
($ x_{1}^{*},x_{2}^{*} $) utilise tout le budget :
- $ p_{1}x_{1}^{*}+p_{2}x_{2}^{*}=m $ (B)
Nous savons donc que $ x_{2}^{*}={\frac {bp_{1}}{ap_{2}}}x_{1}^{*} $ (1) en substituant $ x_{2}^{*} $ dans $ p_{1}x_{1}^{*}+p_{2}x_{2}^{*}=m $ (B).
Nous obtenons alors : $ p_{1}x_{1}^{*}+p_{2}{\frac {bp_{1}}{ap_{2}}}x_{1}^{*}=m $.
Ce qui simplifie : $ x_{1}^{*}={\frac {am}{(a+b)p_{1}}} $
En substituant $ x_{1}^{*} $ dans $ p_{1}x_{1}^{*}+p_{2}x_{2}^{*}=m $, nous obtenons : $ x_{2}^{*}={\frac {bm}{(a+b)p_{2}}} $
Nous avons donc trouvé que le panier préféré pour un consommateur avec des préférence CB de la forme :
- $ U(x_{1},x_{2})=x_{1}^{a}x_{2}^{b} $
est,
- $ (x_{1}^{*},x_{2}^{*})=({\frac {am}{(a+b)p_{1}}},{\frac {bm}{(a+b)p_{2}}}) $
Résumé
[modifier | modifier le wikicode]Une méthode de résolution dans un cas "standard". Il faut utiliser ces deux conditions, toujours vraies à un choix optimal :
- (a) $ p_{1}x_{1}^{*}+p_{2}x_{2}^{*}=m $
- (b) la pente de la droite de budget, $ -{\frac {p_{1}}{p_{2}}} $, et de la CI contenant ($ x_{1}^{*},x_{2}^{*} $) sont égales à ($ x_{1}^{*},x_{2}^{*} $).
Le choix: cas spécifiques
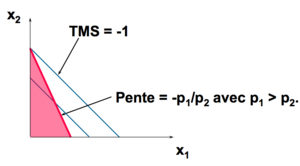
[modifier | modifier le wikicode]Que se passe-t-il si $ x_{1}^{*}=0 $ ?
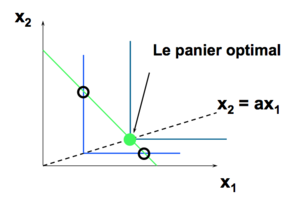
Si un agent ne consomme que d'un bien (et pas du tout de l'autre) nous disons que le panier optimal est une solution de coin.
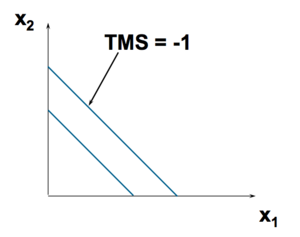
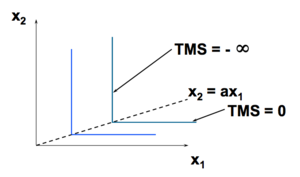
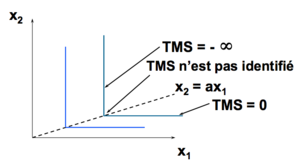
Exemple : Substituts Parfaits
[modifier | modifier le wikicode]
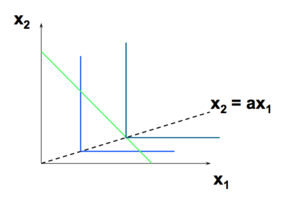
Exemple : Compléments Parfaits
[modifier | modifier le wikicode]- $ U(x_{1},x_{2})=min\{ax_{1},x_{2}\} $
Rappel : Problème de Maximisation
[modifier | modifier le wikicode]Nous avons vu une première méthode de résolution (par substitution).
Une autre méthode, plus générale, est la méthode dite du multiplicateur de Lagrange.
Le Lagrangien s’écrit comme suit:
- $ L=u(x_{1},x_{2})-\lambda (p_{1}x_{1}+p_{2}x_{2}-m) $
Le but est de maximiser directement $ L $, qui contient l’utilité et les contraintes.
Les conditions de premier ordre sont :
- $ {\frac {\partial L}{\partial x_{1}}}={\frac {\partial u}{\partial x_{1}-\lambda p_{1}}}=0 $
- $ {\frac {\partial L}{\partial x_{2}}}={\frac {\partial u}{\partial x_{2}-\lambda p_{2}}}=0 $
- $ {\frac {\partial L}{\partial \lambda }}=p_{1}x_{1}+p_{2}x_{2}-m=0 $
Les deux premières conditions ensemble donnent à nouveau :
- $ {\frac {\frac {\partial u}{\partial x_{1}}}{\frac {\partial u}{\partial x_{2}}}}={\frac {p_{1}}{p_{2}}} $