La Technologie
La firme[modifier | modifier le wikicode]
Après l'analyse du consommateur et de la modélisation de ses choix, nous nous intéressons à la firme.
Très similaire: la firme choisit parmi un ensemble d'alternatives celle qui maximise ses intérêts (i.e. son profit).
Technologie[modifier | modifier le wikicode]
Une technologie est un processus par lequel des inputs sont convertis en output.
E.g. Du travail, un ordinateur, un projecteur, une salle de classe et beaucoup de café sont combinés pour produire ce cours.
Il est possible que plusieurs inputs, ou plusieurs technologies, puissent produire le même output: craie/tableau pour le cours, ou combinaison différente des inputs précédents.
Panier d’inputs[modifier | modifier le wikicode]
dénote la quantité utilisée de l’input ; i.e. des heures de travail.
Un panier d’input est un vecteur des quantités d’input ; (Échec de l’analyse (erreur de syntaxe): {\displaystyle x_1, x_2, … , x_n} ).
E.g. .
Les Fonctions de Production[modifier | modifier le wikicode]
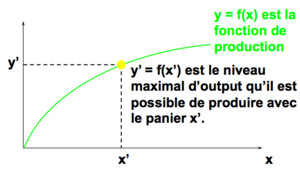
Une fonction de production associée à une technologie donne la quantité maximum d’output qu’il est possible de produire avec un panier d’input.
Si dénote la quantité produite :
Ensemble de technologie[modifier | modifier le wikicode]
Un plan de production est un panier d’inputs et un niveau d’output; (Échec de l’analyse (erreur de syntaxe): {\displaystyle x_1, … , x_n, y} ).
Un plan de production est réalisable si,
- Échec de l’analyse (erreur de syntaxe): {\displaystyle y ≤ f(x_1, ..., x_n)}
L’ensemble de tous les plans de production faisables est un ensemble de technologie.
L’ensemble de technologie est,
- Échec de l’analyse (erreur de syntaxe): {\displaystyle T = \{(x_1, ..., x_n, y) | y ≤ f(x_1, ..., x_n)} et Échec de l’analyse (erreur de syntaxe): {\displaystyle x_1 ≥ 0, ..., x_n, ≥ 0\}}
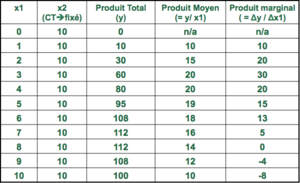
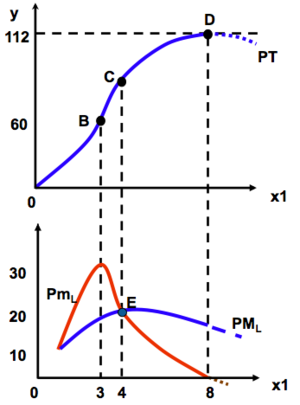
Production à court terme[modifier | modifier le wikicode]
Important:
- Forme de PT
- quand PT atteint son maximum
- Si , alors PML augmente
- Si , alors PML diminue
- </math>PM_L = PmLPM_L</math> au point où PML atteint son maximum
Productivité marginale[modifier | modifier le wikicode]
La productivité marginale d’un input i est la variation d’output y entraîné par la variation de la quantité d’input (ceteris paribus).
- Échec de l’analyse (erreur de syntaxe): {\displaystyle Pm_i = \frac {∂y}{∂x_i}}
E.g. Si,
La productivité marginale du bien 1 est :
- Échec de l’analyse (erreur de syntaxe): {\displaystyle Pm_1 = \frac {∂y}{∂x_1} = \frac {1}{3}x_1^{- \frac {2}{3}}x_2^{\frac{2}{3}}}
La productivité marginale du bien 2 est :
- Échec de l’analyse (erreur de syntaxe): {\displaystyle Pm_2 = \frac {∂y}{∂x_2} = \frac {2}{3}x_1^{\frac {1}{3}}x_2^{- \frac{1}{3}}}
La productivité marginale du bien est décroissante si elle diminue quand on augmente la quantité du bien . C’est le cas standard.
- Échec de l’analyse (erreur de syntaxe): {\displaystyle \frac {∂Pm_i}{∂x_i} = \frac {∂}{∂x_i} (\frac {∂y}{∂x_i}) = \frac {∂^2y}{∂x_i^2} < 0}
E.g. si , alors et , soit Échec de l’analyse (erreur de syntaxe): {\displaystyle \frac {∂Pm_1}{∂x_1} = - \frac {2}{9}x_1^{- \frac {5}{3}}x_2^{\frac {2}{3}} < 0} et Échec de l’analyse (erreur de syntaxe): {\displaystyle \frac {∂Pm_2}{∂x_2} = - \frac {2}{9}x_1^{\frac {1}{3}}x_2^{- \frac {4}{3}} < 0}
Les productivité marginale sont chacune décroissantes.
Une technologie avec plusieurs inputs[modifier | modifier le wikicode]
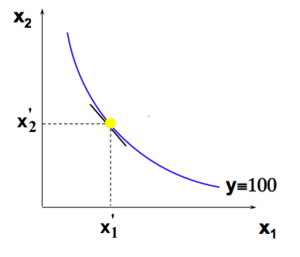
Une isoquante associée à la quantité produite y est l’ensemble de tous les paniers d’Input pouvant produire .
NB: Mêmes propriétés qu’une Courbe d’Indifférence associée à un niveau d’utilité U.
Exemple :
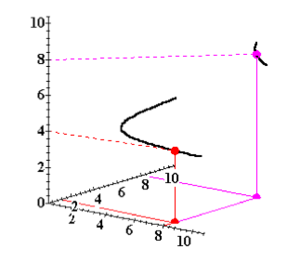
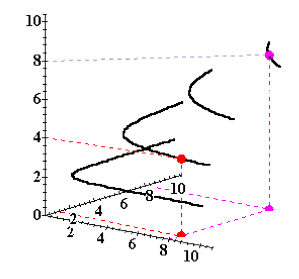
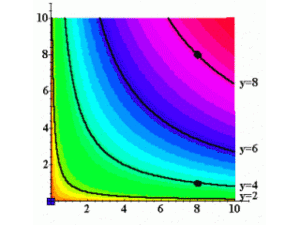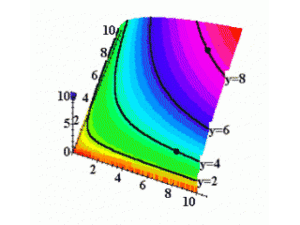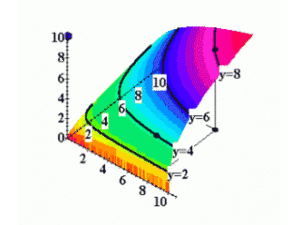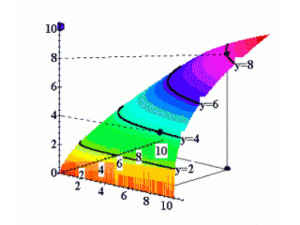
Isoquantes avec 2 inputs variables[modifier | modifier le wikicode]
Tous comme les CI, les isoquantes peuvent être représentées sur un graphe avec la quantité produite sur un axe vertical, et les deux inputs variables sur les axes horizontaux.
La collection complète de toutes les isoquantes est la carte d’isoquantes.
La carte d’isoquante est l’équivalent de la fonction de production
Rendements d’échelle[modifier | modifier le wikicode]
La productivité marginale décrit la façon dont change l'output quand on fait varier un seul input.
Les rendements d'échelles décrit la manière dont change l'output quand tous les inputs changent d'une même proportion.
Si pour tous les paniers (Échec de l’analyse (erreur de syntaxe): {\displaystyle x_1, …, x_n} ), . Alors la technologie décrite par la fonction présente des rendements d'échelle constants.E.g. () en doublant tous les facteurs, on double la production.
Si pour tous les paniers (Échec de l’analyse (erreur de syntaxe): {\displaystyle x_1, …, x_n} ), . Alors la technologie décrite par la fonction présente des rendements d'échelle croissants. E.g. () en doublant tous les facteurs, on fait plus que doubler la production.
Si pour tous les paniers (Échec de l’analyse (erreur de syntaxe): {\displaystyle x_1, …, x_n} ), . Alors la technologie décrite par la fonction présente des rendements d'échelle décroissants. E.g. () en doublant tous les facteurs, on fait moins que doubler la production.
La fonction de production Cobb-Douglas :
Les rendements d'échelles sont :
- constants si Échec de l’analyse (erreur de syntaxe): {\displaystyle a_1 + … + a_n = 1}
- croissants si Échec de l’analyse (erreur de syntaxe): {\displaystyle a_1+ … + a_n > 1}
- décroissants si Échec de l’analyse (erreur de syntaxe): {\displaystyle a_1+ … + a_n < 1} .
NB: Une technologie peut avoir des rendements d'échelles croissants, même si chaque facteur à une productivité marginale décroissante. Intuition ?
E.g. .
Taux marginal de substitution technique[modifier | modifier le wikicode]
Combien la firme doit-elle abandonner d'un input pour rajouter une unité de l'autre input sans changer la quantité produite ?
La pente d'une isoquante est le TMST.
Même calcul que le TMS.
La fonction de production :
Un petit changement () dans le panier de bien crée le changement suivant dans la quantité produite : Échec de l’analyse (erreur de syntaxe): {\displaystyle dy = \frac {∂y}{∂x_1} dx_1 + \frac {∂y}{∂d_2} dx_2} .
Mais le long d'une isoquante (par définition). Donc,
- Échec de l’analyse (erreur de syntaxe): {\displaystyle 0 = \frac {∂y}{∂x_1} dx_1 + \frac {∂y}{∂d_2} dx_2}
- Échec de l’analyse (erreur de syntaxe): {\displaystyle \frac {∂y}{∂d_2} dx_2 = - \frac {∂y}{∂x_1} dx_1}
Soit,
- Échec de l’analyse (erreur de syntaxe): {\displaystyle \frac {dx_2}{dx_1} = - \frac {\frac {∂y}{∂x_1}}{\frac {∂y}{∂x_2}}}
Est donc le taux auquel la firme doit échanger de l'input 2 contre de l'input 1 et garder la production constante..
Technologies "Normales"[modifier | modifier le wikicode]
Une technologie "Normale" est
- continue ;
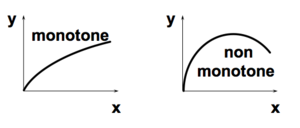
- monotone ;
Convexe.
Monotonie[modifier | modifier le wikicode]
Plus d'un input génère plus de production.
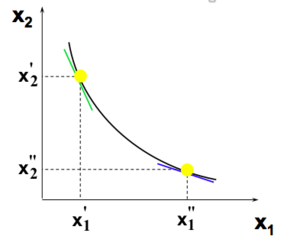
Convexité[modifier | modifier le wikicode]
Si les paniers Échec de l’analyse (erreur de syntaxe): {\displaystyle x’} et Échec de l’analyse (erreur de syntaxe): {\displaystyle x”} produisent chacun y unités d'output, alors la mixture d'input Échec de l’analyse (erreur de syntaxe): {\displaystyle tx’ + (1 - t)x”} produit également au moins y unités d'output pour tout .
Implique que le TMST augmente à mesure que l'on substitue plus de pour du .
Long Terme et Court Terme[modifier | modifier le wikicode]
Le long terme : La firme peut choisir les niveaux d'inputs.
Le court terme : le firme est contrainte dans ses choix d'inputs.
Exemples ?
est la fonction de production de long terme ( et sont variables).
La production de court terme quand est .
La production de court terme quand est