L'Utilité
Les fonctions d'utilité[modifier | modifier le wikicode]
Une fonction d’utilité est un moyen d’assigner un chiffre à chaque panier de consommation possible, de manière à ce que les paniers préférés reçoivent une notation plus élevée que ceux qui leur sont moins préférés.
Modèle du bien être économique d'une personne.
Résultat fondamental: Une relation de préférences complète, réflexive, transitive et continue peut être représentée par une fonction d’utilité continue.
Pour chaque relation de préférence imaginable, remplissant ces critères, vous pouvez trouver une fonction d'utilité continue qui représente cette relation.
Une fonction d'utilité Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle U(x)} représente une relation de préférence Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \succeq} si et seulementt si :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle x' \succ y''} ⟺ Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle U(x') > U(x'')}
- ⟺
- ⟺
L'utilité est un concept ordinal (i.e. un classement).
Si and alors le panier est strictement préféré au panier . On ne peut pas dire que est préféré 3 fois plus que .
Les fonctions d'utilités et les CI[modifier | modifier le wikicode]
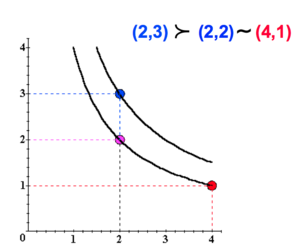
Considérons les paniers (4,1), (2,3) et (2,2). Supposons .
Assignons à ces paniers un chiffre qui préserve le classement des préférences :
e.g. .
Appelons ces chiffres des niveaux d'utilité.
Une CI contient tous les paniers également préférés.
Également préféré => même niveau d'utilité.
Donc tous les paniers sur une CI apporte le même niveau d'utilité.
Les paniers (4,1) et (2,2) sont donc sur la même CI qui apporte U º 4.
Le panier (2,3) est sur la CI qui apporte .
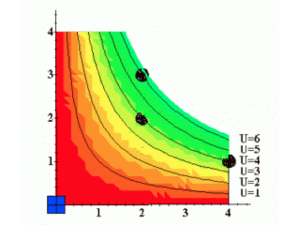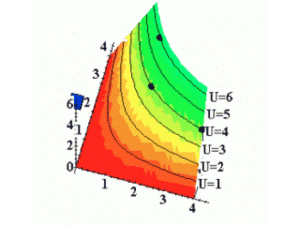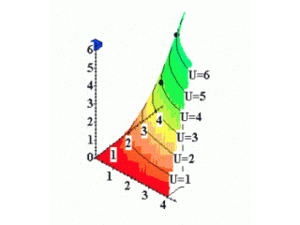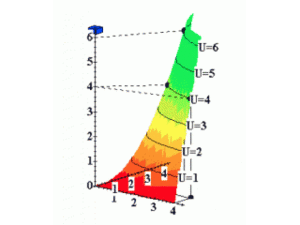
Sur un graphique dans l'espace des biens, cela se représente comme ceci :
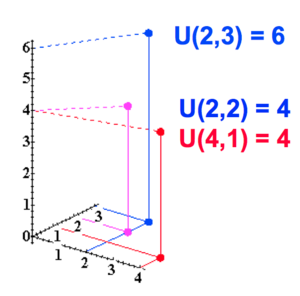
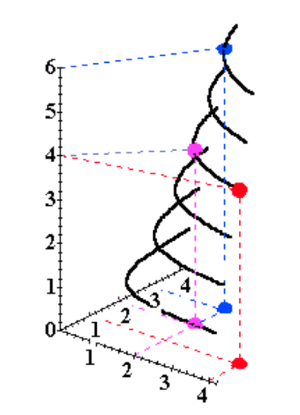
Une autre façon de le visualiser est d'ajouter l'utilité comme un 3ème axe, vertical.
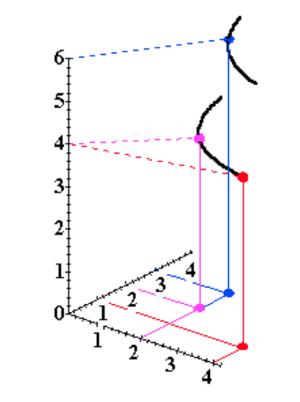
Nous pouvons ajouter les CI sur ce graphique en 3D :
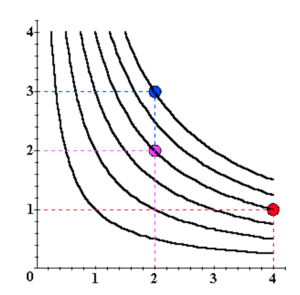
En comparant plus de paniers, nous pouvons obtenir une représentation de plus en plus claire des préférences d'un agent :
En ajoutant un axe vertical représentant l'utilité (3D) :
En comparant l'ensemble total des paniers de bien, nous pouvons avoir l'ensemble des courbes d'indifférence.
Elles représentent complètement les préférences d'un agent.
L'ensemble de toutes les courbes d'indifférence d'une relation donnée est appelé une carte d'indifférence.
Une carte d'indifférence est équivalente à une fonction d'utilité.
Géographes: cela vous rappelle-t-il quelque chose ?
Les fonctions d'utilité[modifier | modifier le wikicode]
Il n'existe pas une unique représentation d'une relation de préférence (important).
Supposons que représente une relation de préférence.
Considérons à nouveau les 3 paniers (4,1), (2,3) et (2,2).
, soit :
- ;
- d'où, .
=> .
Nous avons donc trouvé une fonction d'utilité qui représente la relation de préférence
Maintenant, considérons Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle V = U^2} .
Donc Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle V(x_1, x_2) = x_1^2 x_2^2} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle V(2,3) = 36 > V(4,1) = V(2,2) = 16}
Nous avons donc, une fois encore, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle V(x_1, x_2) = x_1^2 x_2^2} => Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle (2,3) \succ (4,1) \sim (2,2)}
Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle V} préserve le même ordonnancement que U et représente donc les mêmes préférences.
Définissons Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle W = 2U + 10} .
Alors, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle W(x_1, x_2) = 2x_1x_2 + 10} soit, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle W(2,3) = 22 > W(4,1) = W(2,2) = 18} .
Une fois encore Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle (2,3) \succ (4,1) \sim (2,2)} .
Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle W} préserve le même ordonnancement que Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle U} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle V} et représente donc les mêmes préférences.
Toute transformation monotone positive Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle f(u)} d’une fonction d’utilité est elle-même une fonction d’utilité admissible.
On ne peut pas faire de comparaison entre différentes personnes (différentes préférences) en fonction de leur niveau d'utilité !
"Jacques préfère plus le panier (4,2) que Jean car son utilité est de 6 et celle de Jean de 3." n'est pas un raisonnement valide.
Des Bien Substituts[modifier | modifier le wikicode]
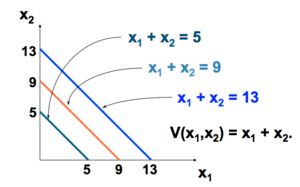
L'utilité pour ces biens substituts s'écrit Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle V(x_1, x_2) = x1_ + x_2} .
Elles sont toutes linéaires et parallèles.
Des biens complémentaires[modifier | modifier le wikicode]
L’utilité pour des compléments parfaits s’écrit : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle W(x_1, x_2) = min\{x_1, x_2\}} .
Quelques autres formes standards[modifier | modifier le wikicode]
Une fonction d’utilité de la forme Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle U(x_1, x_2) = f(x_1) + x_2} est linéaire en Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle x_2} et se dénomme “Utilité Quasi-Linéaire”:.
- E.g. Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle U(x_1, x_2) = 2x_1^{\frac {1}{2}} + x_2} .
Une fonction d’utilité de la forme Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle U(x_1, x_2) = x_1^a x_2^b} avec Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle a > 0} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle b > 0} est dénommée utilité Cobb-Douglas. Une des spécifications les plus utilisée.
- E.g.
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle U(x_1, x_2) = x_1^{\frac {1}{2}} x_2^{\frac {1}{2}}} ; (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle a = b = \frac {1}{2}} )
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle V(x_1, x_2) = x^1 x_2^3} ; (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle a = 1, b = 3} )
Utilité Marginale[modifier | modifier le wikicode]
Marginal signifie “incrémental”.
L’utilité marginale d’un bien Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle i} spécifie la manière dont l’utilité change quand la consommation de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle i} augmente.
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle UM_i = \frac {∂ U(X)}{∂ x_i}}
Hypothèse: typiquement, la satisfaction qu’un agent retire de la consommation d’une unité d’un bien diminue avec les quantités consommées (toutes choses égales par ailleurs).
La non-satiété implique cependant que l’agent est toujours plus heureux avec plus d’un bien.
Cela implique donc que la fonction d’utilité est croissante et concave dans les quantités consommées d’un bien.
L’utilité marginale est donc positive, et sa dérivée négative.
Donc, si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle U(x_1, x_2) = x_1^{\frac {1}{2}} x^{\frac {1}{2}}} , alors :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle UM_i = \frac {∂U}{∂ x_1} = \frac {1}{2} x_1^{-\frac {1}{2}} x_2^{\frac {1}{2}}}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle UM_i = \frac {∂U}{∂ x_2} = \frac {1}{2} x_1^{\frac {1}{2}} x_2^{-\frac {1}{2}}}
Lien entre le TMS et l’Utilité Marginale[modifier | modifier le wikicode]
En allant de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle A} vers Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle C} :
- De Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle A} vers Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle B} on perd de l’utilité
- Perte = Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -\Delta x_2 \times Um_{x_2}}
- De Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle B} vers Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle C} on gagne de l’utilité
- Gain = Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \Delta x_1 \times Um_{x_1}}
- Or, entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle A} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle C} , Perte = Gain
- ⇒ Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -\Delta x_2 \times Um_{x_2} = \Delta x_1 \times Um_{X_1}}
- ⇒ Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {-\Delta x_2}{\Delta x_1} = \frac {Um_{X_1}}{Um_{X_2}}}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle TMXx_1x_2 = \frac {Umx_1}{Umx_2}}
Um et TMS un exemple[modifier | modifier le wikicode]
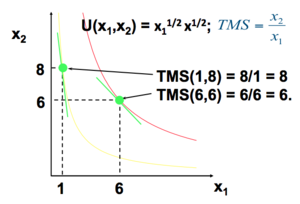
Supposons Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle U(x_1, x_2) = x_1^{\frac{1}{2}} x^{\frac{1}{2}}} . Alors,
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle UM_i = \frac {∂U}{∂ x_1} = \frac {1}{2} x_1^{-\frac {1}{2}} x_2^{\frac {1}{2}}}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle UM_i = \frac {∂U}{∂ x_2} = \frac {1}{2} x_1^{\frac {1}{2}} x_2^{-\frac {1}{2}}}
où,
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle TMS = \frac {\frac {∂U}{∂ x_1}}{\frac {∂U}{∂ x_2}} = \frac {x_2}{x_1}}
Transformation Monotone de l’Utilité et TMS[modifier | modifier le wikicode]
Si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle V = f(U)} , où Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle f(.)} est une fonction strictement croissante, alors :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle TMS = - \frac {\frac {∂V}{∂ x_1}}{\frac {∂V}{∂ x_2}} = - \frac {\frac {f'(U) \times ∂U}{∂ x_1}}{\frac {f'(U) \times ∂U}{∂ x_2}} = - \frac {\frac {∂U}{∂ x_1}}{\frac {∂U}{∂ x_2}}}
Le TMS est inchangé par cette transformation !