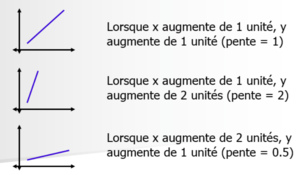
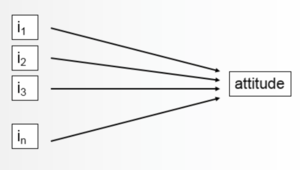
Inférence causale et méthodes quantitatives
Introduction[modifier | modifier le wikicode]
Il y a plusieurs avantages à utiliser des méthodes quantitatives. Elles permettent d’agréger beaucoup d’informations sur beaucoup d’observations ainsi que de résumer et de traiter ces informations. Lorsqu’on utilise ces méthodes statistiques pour faire des inférences causales ou descriptives, il faut accepter certains postulats. Lorsque ces postulats sont respectés, l’inférence causale va être correcte. En acceptant certains postulats, on obtient des informations précises sur notre incertitude. On peut déterminer quelle est la chance de se tromper lorsqu’on fait une inférence de type causale. Ces méthodes traitent de manière très explicite des inférences sur la qualité de l’inférence et sur son incertitude.
Les statistiques sont des méthodes qui résument quantitativement des informations et qui permettent de tirer des constats généraux. L’information brute est appelée « données » qui peuvent provenir d’expérience, de sondage ou de toutes formes d’observations systématiques. Les données organisées de manière systématique forment une banque de données dit aussi une base de données ou un fichier de données.
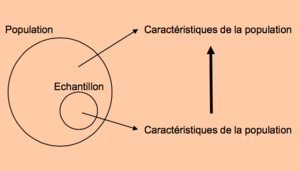
Les données concernant l’ensemble de la population sur laquelle porte l’étude peuvent être introuvables, onéreuses ou impossibles à recueillir. C’est pourquoi on se base sur la sélection d’un échantillon, idéalement selon une procédure de sélection aléatoire qui permet de procéder à des inférences, c’est-à-dire généraliser ce qu’on observe dans l’échantillon à l’ensemble de la population. La population mère est la population sur laquelle porte l’étude et au sein de laquelle est prélevé l’échantillon.
En général, on ne s’intéresse pas aux données pour elles-mêmes, mais à la population dont sont extraites les données. Ainsi, on cherche à inférer de la connaissance sur la population à partir de l’échantillon observé, à savoir les données.
Il existe de nombreuses manières de choisir un échantillon. Plusieurs critères sont pris en considération. Les critères suivants sont en général considérés :
- représentativité de la population étudiée ;
- une fréquence suffisante des caractéristiques d’intérêts : si on étudie le poids des working poors au sein des travailleurs, il faut être sûr d’avoir suffisamment de ces individus dans l’échantillon ;
- facilité de mise en œuvre : il est plus simple d’interroger tous les ménages d’un immeuble plutôt que d’interviewer des individus sélectionnes aléatoirement au sein d’un registre quelconque.
La taille de l’échantillon nécessite également un arbitrage. Plus un échantillon est grand et plus cela permet d’être plus précis et on obtient une erreur d'estimation acceptable, néanmoins, cela est coûteux en argent et en temps.
Idéalement, on aimerait travailler sur un échantillon aléatoire. Un échantillon sélectionné selon une procédure qui assure à chaque membre de la population une probabilité non nulle (et connue) d’être choisi. L’avantage est que l’échantillon aléatoire permet d’exploiter pleinement la théorie statistique. Les outils de la statistique inférentielle s’appuient sur le calcul des probabilités et donc sur l’existence de ces probabilités. Selon la théorie statistique, il n’est pas nécessaire d’observer tout le monde, un échantillon convenablement choisi peut fournir des résultats très proches de ceux d’une analyse de toute la population. C’est une analyse exhaustive.
Les échantillons non-aléatoires sont un choix raisonné comme par exemple on interroge les personnes qui paraissent a priori les plus intéressantes (experts d’un domaine, etc.) ou encore une liste choisie au hasard dans l’annuaire téléphonique avec un échantillon aléatoire des inscrits dans l’annuaire, mais cela exclut les personnes non inscrites. L’enquête par quotas se compose d’un échantillon sur la base des caractéristiques connues de la population-mère. Lorsqu’un quota est rempli, par exemple les jeunes âgés entre 18 et 30 ans, on ne peut plus interviewer de jeunes de cet âge. Donc ce n’est pas purement aléatoire. Ce sont des méthodes lorsqu’on utilise la statistique différentielle.
Le problème des échantillons non-aléatoires est qu’on ne sait pas mesurer la fiabilité des résultats. Si on applique quand même les outils de l’inférence statistique, on obtient des significativités non-rigoureuses. Elles ne donnent que des indications approximatives et doivent être considérées avec prudence.
L’unité d’analyse ou l’unité d’observation est l’objet, la personne ou l’évènement dont on étudie les caractéristiques. Cela peut être les individus, les pays, les cantons, les entreprises, les conflits violents, les familles, les universités, les éditoriaux ou encore les élections présidentielles. On peut par exemple fait une étude sur les journaux est analyser les éditoriaux. C’est la question de recherche et le phénomène étudié qui va définir l’unité d’analyse pertinente.
Données[modifier | modifier le wikicode]
Variables et niveaux de mesure[modifier | modifier le wikicode]
Dans Guide Pratique d'introduction à la régression en sciences sociales publié en 2009, Pétry et Gélineau définissent une variable comme un regroupement logique de caractéristiques décrivant un phénomène observable empiriquement. Si la caractéristique mesurée peut prendre différentes valeurs, on dit que cette caractéristique est une variable. Cette caractéristique doit posséder au moins deux valeurs. Donc, les variables sont les attributs qui caractérisent les unités d’analyse (observations, individus, cas, etc.). Une variable est un critère par lequel on classe des observations dans des catégories comme par exemple le sexe, le niveau de formation, le pays d’origine, le type de régime politique, le PNB par habitant ou encore le revenu. Ce qui rend utile scientifiquement une variable est sa mesure.
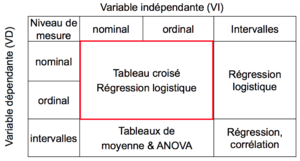
Les variables peuvent posséder des propriétés différentes qui vont définir leur niveau de mesure. Les trois niveaux de mesure les plus courants en sciences sociales sont :
- nominal : qualitative ou catégorielle ;
- ordinal : qualitative ou catégorielle ;
- intervalles : quantitative ou continue.
Variable nominale[modifier | modifier le wikicode]
Une variable nominale est classement des observations dans des catégories. Ces catégories sont mutuellement exclusives. Par exemple, on est soit un homme, soit une femme; un pays est soit une démocratie, soit une dictature. Les valeurs nominales sont des catégories sans ordre. Lorsqu’on assigne des nombres aux valeurs nominales, c’est- à-dire aux catégories d’une variable nominale, ces nombres sont arbitraires. On ne peut pas leur faire subir d’opération arithmétique.
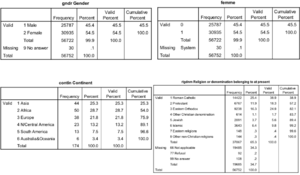
Les variables de type catégoriel (qualitative) sont par exemple la religion, le sexe, la langue, la nationalité ou encore la région. La variable sexe est habituellement une variable dichotomique qui prend deux valeurs.
Variable ordinale[modifier | modifier le wikicode]
Une variable ordinale est un classement des observations dans des catégories ordonnées ou hiérarchique voire même chronologique. Les valeurs peuvent être ordonnées. On peut assigner à ces valeurs des nombres qui indiqueraient leur ordre. On ne peut pas leur faire subir d’opération arithmétique.
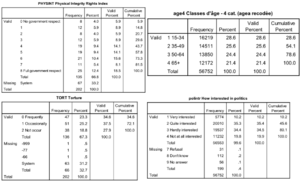
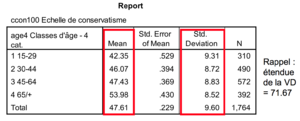
Une variable de type catégoriel (qualitative) est par exemple le niveau de formation, les classes d’âge, les classes de revenu, l’intérêt pour la politique, le type de régime politique (démocratique, partiellement démocratique, non démocratique). Les variables ordinales fournissent plus d’informations que les variables nominales.
Variable d’intervalle[modifier | modifier le wikicode]
Outre les propriétés des variables nominale et ordinale, une variable d’intervalle suppose que la distance (l’intervalle) entre les valeurs est quantifiable (les intervalles sont égaux). Un exemple est la variable « âge » qui est un x, l’intervalle entre 50 ans et 80 ans est de 30 ans. Les valeurs peuvent correspondre à une unité de mesure standard, à une métrique spécifique. Dans ce cas, le score attribué à chaque individu se réfère directement à la caractéristique mesurée par la variable. Par exemple, la variable « revenu en francs suisses » a pour unité de mesure le franc suisse; la variable « âge » a pour unité l’année; la variable « taux de participation » a pour unité le pourcentage.
Les variables d’intervalles permettent de faire des opérations arithmétiques. Ce sont des variables quantitatives, par exemple l’âge, le nombre d’années d’étude, le revenu, le PIB par habitant ou encore le taux de participation.
Variable ordinale métrique[modifier | modifier le wikicode]
Une variable ordinale métrique n’est pas un niveau de mesure à proprement parler. On fait l’hypothèse qu’il y a une distance équivalente entre les valeurs de la variable ordinale (les intervalles entres les valeurs sont identiques), c’est-à- dire que la variable possède les propriétés d’une variables d’intervalles.
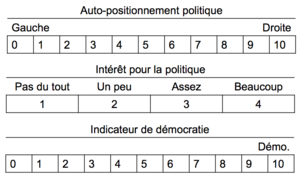
Concernant la de variable d’auto-positionnement on peut être tenté d’utiliser une moyenne supposant que les intervalles sont égaux et que la variable sur laquelle on va calculer la moyenne est une variable d’intervalle. Il faut supposer qu’entre les intervalles, la distance entre 0 et 1 est la même qu’entre 1 et 2.
Pour déterminer si une variable est ordinale métrique, il y a plusieurs éléments dont la distribution des observations. Des mesures sont préalablement faites par les chercheurs mais parfois ce sont des mesures qui ne sont pas très bien faites.
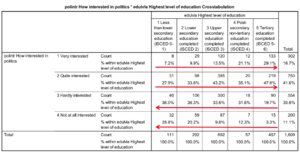
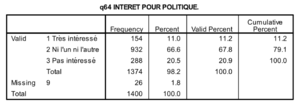
Pour l’intérêt pour la politique,
Si la variable est ordinale :
Si la variable est ordinale métrique :
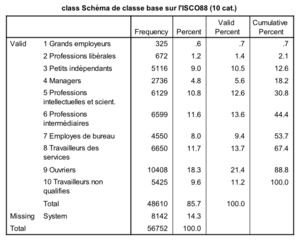
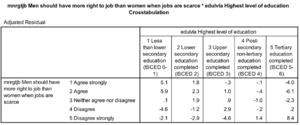
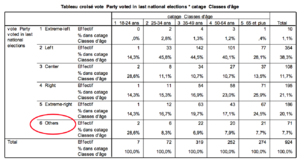
Ce schéma de classe social est bien détaillé. On pourrait essayer d’argument que la variable est ordinale mais pour cela on suppose que les grands employeurs se situent au sommet de la hiérarchie sociale jusqu’aux travailleurs non qualifiés qui sont en bas de la hiérarchie sociale.
Le niveau de mesures permet une anticipation des problèmes mais aussi opérationnalisation des concepts, le choix des techniques statistiques ainsi que le choix des coefficients d’association et des tests statistiques appropriés.
Matrices de données[modifier | modifier le wikicode]
Les données statistiques sont habituellement organisées comme des tableaux ou des matrices dans lesquelles :
- les lignes représentent les unités d’observations (individus, pays, entreprises, conflits violents, etc.), ou unité d’analyse. L’unité d’analyse est l’objet ou la personne dont on étudie les caractéristiques ;
- les colonnes représentent les variables ou les caractéristiques des unités d’observations comme par exemple le sexe, l’âge, le vote ou encore le PNB.
Les codes sont parfois directement interprétables comme par exemple l’âge, le revenu en dollars ou encore le PIB par habitant. D’autres fois, leur signification renvoient à un libellé par exemple : 1 pour les hommes et 2 pour les femmes; 1 pour les mariés, 2 pour les célibataires, 3 pour les divorcés/séparés et 4 pour les veufs. Certains codes sont spécifiques et peuvent signifier que la question ne s’applique pas, que l’interviewé a refusé de répondre, qu’il ne connaît pas la réponse, que l’information est manquante avec des codes tels que 98, 99, 999, -1, -2, -66. -77, -88, -99, - 999, - 9999. Si on ne dispose pas l’information, on ne peut pas analyser. On retrouve souvent des données manquantes par rapport à la variable/caractéristique mesurée. Ces données manquantes sont définies de manières variées.
Les informations sont la plupart du temps codés d’une manière numérique parce que les logiciels sont plus efficaces lorsqu’ils utilisent des valeurs numériques.
SPSS[modifier | modifier le wikicode]
SPSS est un logiciel pour le traitement et l’analyse statistique de données. Il permet de gérer de grandes bases de données (individus x variables). L’analyse statistique et le traitement informatique des données ne sont que des outils au service du chercheur
Le logiciel SPSS se compose de trois fenêtres principales :
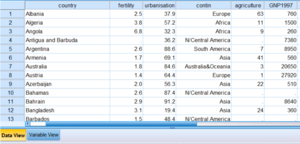
- l’éditeur des données (Data Editor) qui contient deux onglets avec la matrice des données (Data View) et le dictionnaire des variables (Variable View) ;
- la fenêtre des résultats (Viewer ou Output) ;
- la fenêtre de syntaxe (Syntax Editor)
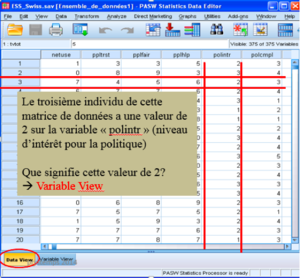
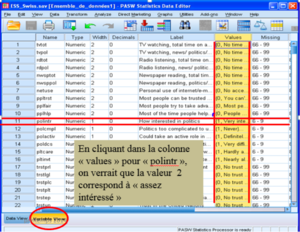
Chaque fenêtre est à sauvegarder indépendamment des autres. En lignes on retrouve les observations (ici ce sont les individus interrogés) et en colonnes les variables (ici,« polintr », l’intérêt pour la politique).
En lignes sont les variables (ici la variable « polintr »), en colonnes les caractéristiques des variables (ici « values », valeurs des modalités). « Name » se réfère au nom des variables, « Type » au type de variable (numérique, caractère, date, etc.), «Label» au libellé des variables, « Values » aux valeurs et libellés, comme « Missing » aux valeurs données manquantes définies.
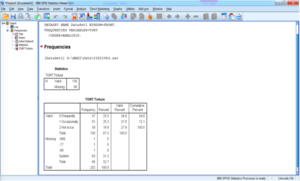
La fenêtre des résultats affiche les lignes de commandes qui ont produits les résultats, les résultats des analyses ainsi que les éventuels messages d’erreur.
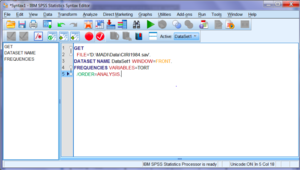
La fenêtre « Syntax Editor » permet d’écrire directement les instructions en langage SPSS sans passer par les menus.
Outils statistiques de base[modifier | modifier le wikicode]
Les pourcentages[modifier | modifier le wikicode]
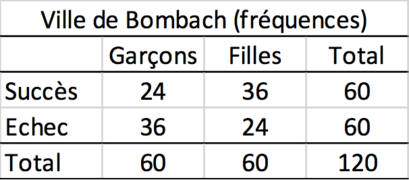
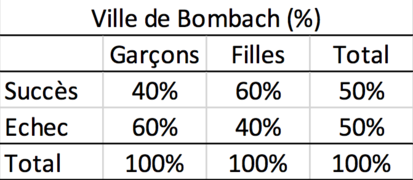
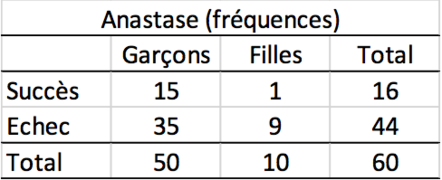
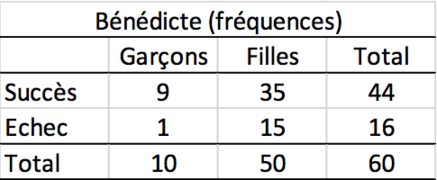
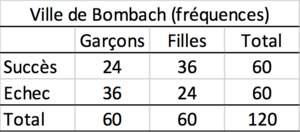
Quand les fréquences sont élevées, la comparaison est difficile. Comparer deux fréquences qui proviennent de groupes comportant un nombre de cas sensiblement différents est difficile.
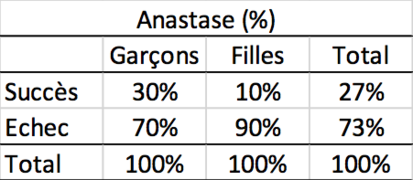
En terme de fréquence, le nombre total varie fortement. Pour comparer des fréquences qui proviennent de groupes, on calcule les pourcentages. Un pourcentage est une forme de standardisation. Quel serait le nombre de fréquence si le nombre total de cas était de 100.
Il faut toujours être prudent lorsqu’on calcule des pourcentages. Les pourcentages sont assez instables. Si il y a une erreur de codage des données, le pourcentage peut varier.
Diagrammes circulaires (camemberts)[modifier | modifier le wikicode]
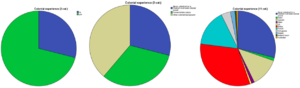
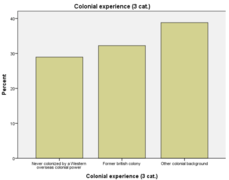
Il existe de nombreux types de variables comme les analyses univariées ou encore les analyses bivariées. Le cercle représente le nombre total d’observations, ici les pays. Les tranches peuvent représenter soit des pourcentages, soit des fréquences. Le diagramme circulaire est adapté pour les variables nominales et ordinales si il n’y a pas trop de modalités. Plus grand est le pourcentage et plus grand est le camembert.
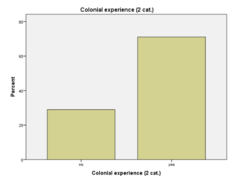
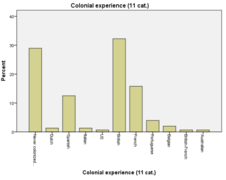
Diagrammes à barres (ou en bâtons)[modifier | modifier le wikicode]
Les digrammes à barres sont adaptés pour des variables nominales et ordinales.
Les histogrammes[modifier | modifier le wikicode]
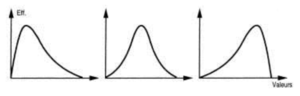
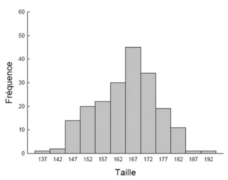
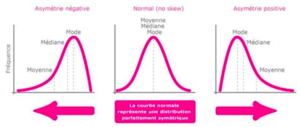
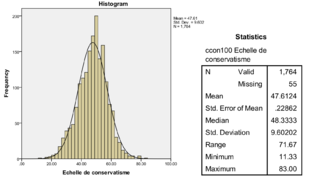
Les histogrammes sont adaptés pour des variables d’intervalles. Ils permettent de visualiser la forme de la distribution qui est symétrique ou non et les concentrations et discontinuités sur l’échelle. Lorsqu’on parle de forme distribution, cela signifie la manière dont est distribuée notre observation sur une échelle.
La distribution de gauche est une distribution asymétrique. Celle du milieu est parfaitement symétrique et la distribution de droite est asymétrique.
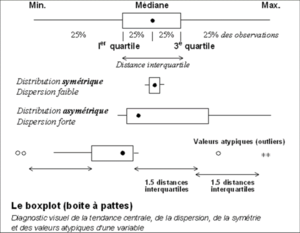
Boxplots[modifier | modifier le wikicode]
Les boxplots sont aussi appelés « boîtes à pattes » ou « boîtes à moustaches ». Ils sont adaptés pour des variables d’intervalles et permettent de visualiser la forme de la distribution (symétrique ou non), les concentrations et discontinuités sur l’échelle. Les boxplots sont particulièrement utilisés pour distinguer deux groupes différents.
Le premier boxplot est une distribution symétrique. Le principe du boxplot est de résumer la distribution des observations sur une variable. Il y a les pattes et les extrémités qui indiquent la valeur minimum et la valeur maximum. Le point indique la valeur de la médiane. Les bords des boites définissent le premier et le troisième quartile.
Pour déterminer si une distribution est symétrique, il faut :
- regarde si le point est au centre de la boite ;
- regarder si les pattes ont la même longueur ;
- regarder s’il y a des valeurs atypiques : si une valeur dépasse plus de 1,5 fois la valeur de la
boite, c’est une valeur atypique. Si une valeur dépasse plus de 3 fois la valeur de la boite, c’est une valeur extraordinaire.
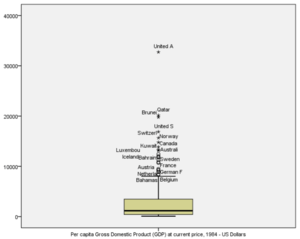
Lorsqu’on a un boxplot ou un histogramme, il faut regarder l’échelle. On voit la forte concentration des pays. Entre la médiane est la patte, on a la moitié des observations. Les pattes ne sont pas de la même longueur, la médiane est hors de la boite, on a beaucoup de valeurs extraordinaires.
Il faut se poser la question de savoir si la distribution est symétrique. Sur la variable âge, le boxplot permet de mettre en évidence l’individu qui a 120 ans. 
Les cas déviants[modifier | modifier le wikicode]
Les histogrammes et surtout les boxplots permettent de déceler les cas déviants qu’on appel aussi les « outliers ». Les cas déviants, ont des cas et des observations dont la valeur est isolée et paraît anormalement enlevée ou basse. Un cas est considéré comme déviants lorsqu’il se retrouve éloigné aux extrémités d’une distribution, détachés de la plupart des autres valeurs comme par exemple le revenu très élevé d’un PDG.
Les cas déviants peuvent affecter les analyses statistiques. Il faut chercher à comprendre pourquoi ils sont déviants. Cela peut être des erreurs dans la mesure ou encore dans la compilation des données. Il est possible d’exclure les cas déviants des analyses mais seulement après avoir compris leur signification.
Mesures de tendance centrale[modifier | modifier le wikicode]
Une mesure de tendance centrale est une valeur typique ou représentative d’un ensemble de score. Elles résument en quelque sorte le « milieu » d’une distribution ou sa valeur « moyenne » :
- mode ;
- médiane ;
- moyenne arithmétique.
Mode[modifier | modifier le wikicode]
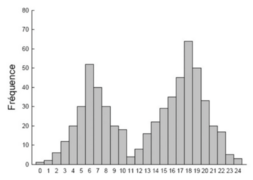
Le mode correspond à la modalité d’une variable donnée qui contient le plus d’observations pour les variables nominales, ordinales et d’intervalles mais de peu d’intérêt pour les variables d’intervalles. Les distribution s’opère entre unimodale (graphique à gauche) et bimodale (à droite).
Médiane[modifier | modifier le wikicode]
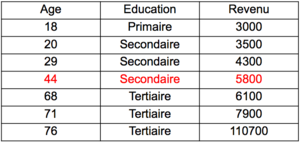
Lorsque les scores sont ordonnés, la médiane est la valeur qui divise en deux parties égales un ensemble ordonné de scores pour les variables ordinales et d’intervalles car les scores doivent être ordonnés. Une variable nominale n’a pas de médiane. C’est la valeur de l’observation qui partage la distribution en deux parties contenant chacune 50 % des observations. Il faut que les scores soient ordonnés, du plus petit au plus grand. La médiane est le score qui se situe au milieu. Le score médian se calcule selon la formule Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {N + 1}{2}} où Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle N} représente le nombre d’observations. La médiane n’est pas affectée par les scores ou valeurs extrêmes à savoir les cas déviants. La médiane est plus robuste que la moyenne.
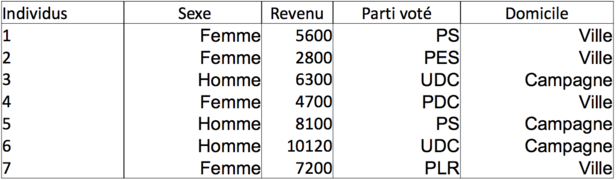
Dans cet exemple, il y a trois variables (une est ordinale, deux sont d’intervalles) et sept observations qui sont les individus). Le score médian se calcule comme suit : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {N + 1}{2} = \frac {7 + 1}{2} = 4} , soit le quatrième score.
Moyenne[modifier | modifier le wikicode]
La moyenne est la somme de tous les scores divisés par le nombre de scores. La formule de la moyenne pour un échantillon est Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {𝑋} = \frac {Σx_i}{N}\times \hat {𝑋}} («x-barre») indique la moyenne d’un échantillon. La formule de la moyenne pour une population est Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝜇 = \frac {Σx_i}{N}} , le symbole Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝜇} (« mu ») indique la moyenne d’une population. L’indice Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑖} de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_i} désigne les scores individuels. Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_1} est le premier score, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_2} le second, etc. Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Σ} (sigma) est utiliser pour indiquer la somme de tout ce qui suit ce caractère. Ainsi, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Σ𝑋_i} signifie la somme de tous les scores individuels pour des variables d’intervalles (quantitatives).
Contrairement au mode et à la médiane, la moyenne est une mesure qui incorpore la totalité des scores. Elle comporte donc plus d’informations. La moyenne est sensible aux scores extrêmes, c’est-à-dire aux scores très bas ou très élevés. Par exemple, la présence de très hauts revenus ou leur absence aura des effets sur la moyenne. Dans certains cas, la moyenne ne représente pas vraiment un score typique.
Si on supprime ces cas déviants, par exemple les très hauts revenus, la moyenne peut changer ce qui n’est pas le cas de la médiane.
Mesures de variation/dispersion[modifier | modifier le wikicode]
Les mesures de variation indiquent le degré de concentration ou de dispersion de la distribution d’une variable. Elles indiquent dans quelle mesure les scores sont semblables ou différents les uns des autres :
- étendue ;
- écart-type ;
- variance.
Étendue[modifier | modifier le wikicode]
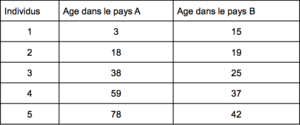
L’étendue est une mesure de distance entre la valeur la plus élevée et la valeur la plus basse d’une distribution. Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐸𝑡𝑒𝑛𝑑𝑢𝑒\ = 𝑣𝑎𝑙𝑒𝑢𝑟\ 𝑚𝑎𝑥𝑖𝑚𝑢𝑚\ – 𝑣𝑎𝑙𝑒𝑢𝑟\ 𝑚𝑖𝑛𝑖𝑚𝑢𝑚} . Plus l’étendue est grande, plus la dispersion est importante. Utile pour comparer des pays ou des groupes.
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle É𝑡𝑒𝑛𝑑𝑢𝑒\ 𝑑𝑢\ 𝑝𝑎𝑦𝑠\ 𝐴 = 78 – 3 = 75}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle É𝑡𝑒𝑛𝑑𝑢𝑒\ 𝑑𝑢\ 𝑝𝑎𝑦𝑠\ 𝐵 = 42 – 15 = 27}
Variance[modifier | modifier le wikicode]
La variance est égale à la moyenne des carrés des écarts entre chaque observation et la moyenne des observations. Pour une population, la formule est Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝜎^2 = \frac {(X_i - 𝜇)^2}{N}} et pour une échantillon Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle S^2 = \frac {(X_i - \hat {x})^2}{N - 1}} . Plus il y a de variation plus la dispersion sera grande.
Écart-type (standard déviation)[modifier | modifier le wikicode]
L’écart-type est la racine carrée de la variance, c’est-à-dire de la moyenne des carrés des écarts entre chaque observation et la moyenne des observations. Pour une population la formule est Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝜎 = \sqrt {𝑣𝑎𝑟𝑖𝑎𝑛𝑐𝑒}} et pour un échantillon, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑠 = \sqrt {𝑣𝑎𝑟𝑖𝑎𝑛𝑐𝑒}} .
Comme la moyenne et l’étendue, la variance et l’écart-type sont sensibles aux valeurs extrêmes alors ces indicateurs sont instables et peu robustes. Plus il y a de variation entre les scores, plus la somme des carrés sera grande, et plus la variance et l’écart-type seront grands.
L’inconvénient de la variance est qu’en mettant à la puissance 2 (au carré) les écarts par rapport à la moyenne sans les remettre ensuite en base 1, elle s’exprime dans une échelle différente de celle des scores. L’avantage de l’écart-type est qu’il remet en base 1 un nombre préalablement élevé à la puissance 2 et s’exprime ainsi dans la même échelle de celle des scores. Si la variable est l’âge (donc l’unité de mesure est l’année), l’écart-type est exprimé dans la même échelle d’années que l’âge des répondants. On peut ainsi considérer l’écart-type comme l’écart.
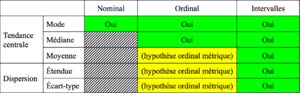
Récapitulatif[modifier | modifier le wikicode]
Corrélation et régression linéaire[modifier | modifier le wikicode]
Corrélation et régression linéaire simple[modifier | modifier le wikicode]
La corrélation et régression linéaire simple permettent d’examiner la relation (l’association) entre deux variables d’intervalles (quantitatives).
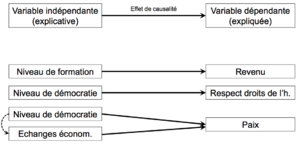
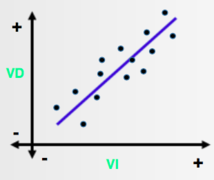
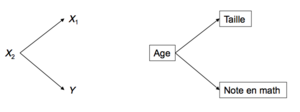
L’idée est de découvrir si la position des individus (pays, entreprises, etc.) sur une variable influence leur position sur la deuxième. Parfois, on cherche à déterminer si deux variables sont associées l’une à l’autre sans se soucier de la causalité. La plupart du temps, on s’intéresse aux relations causales dans lesquelles on fait l’hypothèse qu’une variable indépendante (VI) affecte une variable dépendante (VD). La variable indépendante est la variable explicative dit aussi la cause et la variable dépendante et la variable que l’on cherche à expliquer.
On peut faire l’hypothèse que le niveau de revenu dépend du niveau de formation et que le niveau de bonheur dépend du revenu. Dans ce schéma le niveau de formation influence le niveau de revenu.
Toutes les méthodes statistiques qui vont permettre de tester une hypothèse sur un lien de causalité entre une variable indépendante et une variable dépendante ou entre plusieurs variables indépendantes et dépendantes reposent sur six questions clés concernant la relation entre deux variables :
- existe-t-il une relation entre les deux variables pour les données que nous analysons ?
- quelle est la force ou l’intensité de cette relation ?
- quelles sont la direction et la forme de la relation ?
- si une relation existe et si on travaille avec des données d’échantillon, peut-on généraliser la relation à la population de laquelle est tiré l’échantillon ?
- la relation est-elle véritablement causale ? Ou n’est-elle pas plutôt une relation fallacieuse engendrée par une quelconque tierce variable ?
- quelles sont les variables intermédiaires qui relient la VI et la VD ?
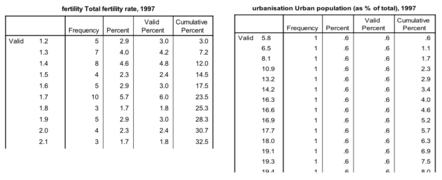
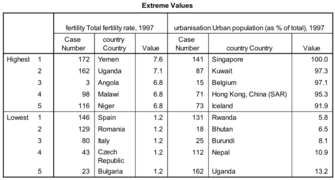
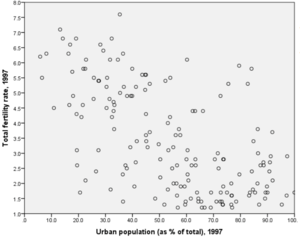
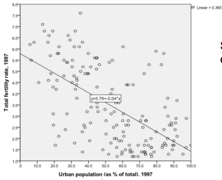
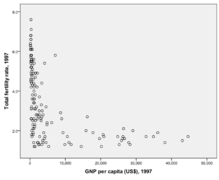
On s’intéresse à la relation entre le taux de fertilité et le taux d’urbanisation. Est-ce que les pays les plus urbanisés ont véritablement un taux de fertilité plus faible ? On formule l’hypothèse suivante : plus le taux d’urbanisation augmente, plus le taux de fertilité diminue. On postule une relation négative.
Les données vont permettre de tester cette hypothèse.
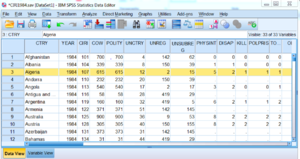
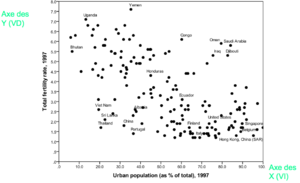
Un diagramme de dispersion permet de mesurer des variables dans un intervalle. Dans ce diagramme, l’Albanie a un taux de fertilité de 2,5% et urbanisé à 37,9%. L’idée est de representer l’ensemble des pays.
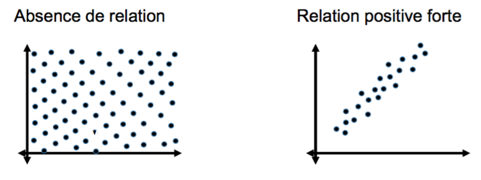
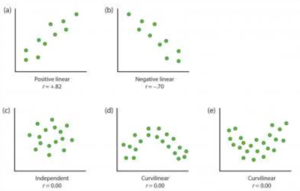
Ces digrammes donnent un bon aperçu entre deux variables d’intervalles. Si la relation est positive, les valeurs les plus basse de la variable intendante donc le taux de fertilité sont associées aux valeurs les plus basses et inversement. L’hypothèse est que plus le taux d’urbanisation augmente, plus le taux de fertilité diminue. La forme du nuage de points nous indique une relation négative entre les deux variables. Les points se situent sur une diagonale allant du point supérieur gauche au point inférieur droit avec des pays qui s’en écartent mais pour des raisons particulières.
Le diagramme de dispersion représente chaque observation par un point dans un espace bidimensionnel. Les coordonnées de chaque point (Xi, Yi) correspondent aux valeurs obtenues par une observation (par exemple un pays) pour les variables X et Y. Ce graphique permet de visualiser la direction de la relation (positive ou négative), d’en évaluer visuellement la force (si la relation linéaire est parfaite, les points forment une droite) et d’établir un diagnostic concernant la présence de valeurs atypiques.
L’hypothèse est que plus le taux d’urbanisation augmente, plus le taux de fertilité diminue :
- Tendance ? relation négative ;
- Dispersion ? relative forte dispersion ;
- Cas extrêmes ? il est possible de distinguer des points qui s’écartent de cette droite.
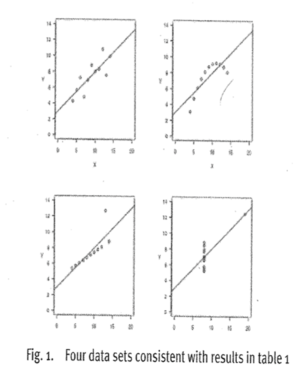
Un diagramme de dispersion est adapté lorsqu’on a peu d’informations. Il est possible de distinguer une relation entre deux variables mais dans certains cas on ne peu rien observer.
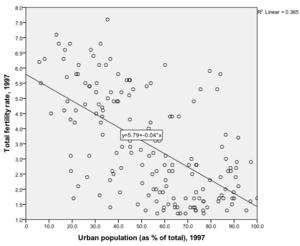
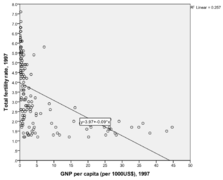
Un outil pour visualiser graphiquement la tendance est la droite de régression qui décrit beaucoup mieux la relation.
La droite de régression (droite des moindres carrés) est la droite qui résume la distribution des observations dans le diagramme comme étant linéaire.
Elle est calculée par la méthode des moindres carrés. C’est la droite qui minimise la somme des carrés des distances entre la droite et la valeur de la VD de chacune des observations. Autrement dit, c’est la droite qui minimise la distance de l’ensemble des points par rapport à elle-même. Les deux variables sont d’intervalles (quantitatives).
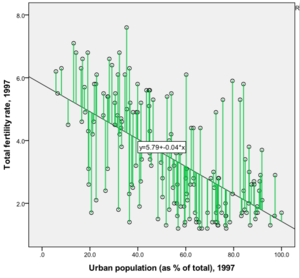
Les lignes verticales en vert indiquent la distance entre les pays et la droite de régression qui résume la relation urbanisation à fertilité.
Ces distances sont appelées « résidus ». Lorsqu’on trace une droite de régression, on construit un modèle. Un modèle simplifie la réalité mais on ne résume pas toute la relation. Si on met ces distances au carré, puis qu’on les additionne, la somme obtenue serait inférieure à celle de n’importe quelle autre droite qu’on pourrait tracer.
La relation entre deux variables d’intervalles peut s’écrire de la manière suivante :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌_i = 𝑏_0 + 𝑏_1 𝑋_1 + 𝑒_i}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌_i} = valeur observée de la VD d’une observation.
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑏_0} = constante qui indique la valeur à l’ordonnée pour une abscisse nulle (valeur de Y quand X = 0), parfois noté Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑎} .
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑏_1} = coefficient de la pente de la droite de régression.
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_i} = valeur observée de la VI d’une observation .
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑒_i} = résidu (estimation de l’erreur) d’une observation Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle i} .
L’équation de la droite de régression prend la forme algébrique suivante
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat{𝑌}_i = 𝑎+ 𝑏_1 𝑋_i}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat{𝑌}_i = 𝑏 + 𝑏_1 𝑋_i}
Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} = valeur estimée de la VD par la droite de régression.
La pente est le changement de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} pour chaque changement d’une unité de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle X} . Pour rappel, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑏 = \frac {Δ Y}{Δ X}}
 La valeur de la pente qu’on appelle aussi coefficient de régression indique la mesure du changement sur la VD d’un changement d’une unité de la VI. Le signe (+ ou −) du coefficient indique la direction de ce changement, c’est-à-dire le sens de la relation. Il faut connaître les unités de mesure de la VD et de la VI :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑢𝑛𝑖𝑡é\ 𝑑𝑒\ 𝑚𝑒𝑠𝑢𝑟𝑒\ 𝑑𝑒\ 𝑙𝑎\ 𝑓𝑒𝑟𝑡𝑖𝑙𝑖𝑡é = 𝑙𝑒\ 𝑛𝑜𝑚𝑏𝑟𝑒\ 𝑚𝑜𝑦𝑒𝑛\ 𝑑’𝑒𝑛𝑓𝑎𝑛𝑡𝑠\ 𝑝𝑎𝑟\ 𝑓𝑒𝑚𝑚𝑒} ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑢𝑛𝑖𝑡é\ 𝑑𝑒\ 𝑚𝑒𝑠𝑢𝑟𝑒\ 𝑑𝑒\ 𝑙’𝑢𝑟𝑏𝑎𝑛𝑖𝑠𝑎𝑡𝑖𝑜𝑛 = 𝑙𝑒\ 𝑝𝑜𝑢𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒} .
SPSS calcule la valeur de la constante et celle du coefficient de régression :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌 = 5.79 + (−0.04)𝑋_1}
Equation de régression :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat{𝑌} = 𝑏_0 + 𝑏_1𝑋_i}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌 = 5.79 + (−0.04)𝑋_i}
:Interprétation de la constante : ( Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑏_0 = 5.79} ) : lorsque le taux d’urbanisation (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋} ) est égal à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} , le taux de fertilité est de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 5.79} enfants par femme.
- Interprétation du coefficient de régression :
(Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑏_0 = −0.04} ) : lorsque le taux d’urbanisation (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋} ) augmente d’une unité, c’est-à-dire d’un point de pourcentage, le taux de fertilité diminue de 0.04 enfant par femme. Si par exemple, le taux d’urbanisation (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋} ) d’un pays augmente de 25 points de pourcentage, on s’attendrait à ce que les femmes aient en moyenne un enfant de moins. Une augmentation de 25 unités de la VI produirait une diminution de 1 sur la Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle VD : 25 \times −0.04 = 1} . Cela traduirait un déclin important du taux de fertilité.
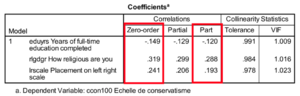
Le coefficient de Pearson (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑟} ) est un coefficient d’association qui permet d’apprécier l’intensité (la force) d’une relation. Il mesure le degré de concentration des points (observations) le long de la droite de régression. Si les points se regroupent de manière étroite le long de la droite de régression, le r sera élevé, ce qui indique une forte relation.
Le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒓} varie de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle −𝟏.𝟎𝟎} à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle +𝟏.𝟎𝟎} :
- quand Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒓 = −𝟏} ou Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒓 = 𝟏} , la relation est parfaite ;
- quand Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒓 = 𝟎} , il n’y a pas de relation entre les deux variables.
Plus le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑟} s’approche de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle −1} ou de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} , plus la relation est forte.
Le signe indique le sens de la relation (négative ou positive). La grandeur mesure la force de la relation. À partir de quelle valeur le 𝑟 indique une forte relation ? Et une relation modérée ? Il n’y a pas de règles en la matière. Cela dépend des attentes, de ce que suggère la théorie et des résultats obtenus par d’autres chercheurs. Avec des données agrégées (par exemple les pays), le 𝑟 tend à être beaucoup plus élevé qu’avec des données individuelles (dont l’unité d’analyse est l’individu).
Le 𝒓 est une mesure symétrique d’association peu importe quelle variable est indépendante et laquelle est dépendante.
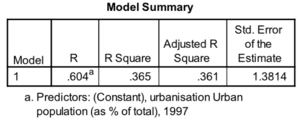
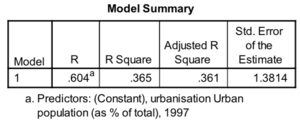
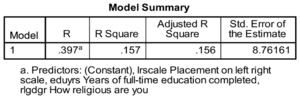
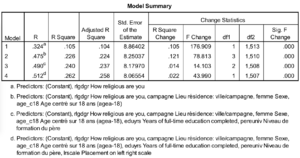
Lorsqu’on procède à une régression, cela est un modèle. Le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑹} correspond au coefficient de corrélation de Pearson. Le coefficient Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑹^𝟐} ( 𝑅 Square dans SPSS) indique le pouvoir explicatif du modèle, c’est-à-dire la proportion de la variation de la VD expliquée par la VI. Ce coefficient est une proportion qui varie de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} .
On le traduit souvent en pourcentage :
- dans cet exemple, l’urbanisation explique 36.5% de la variance du taux de fertilité ;
- il s’ensuit que Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1 – 𝑅^2} est la proportion de la variation de la VD qui n’est pas expliquée par la VI. Dans notre exemple, 63.5% de la variation dans le taux de fertilité n’est pas expliquée par le taux d’urbanisation (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1 – 0.365 = 0.635} ).
Le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑹^𝟐} ajusté (Adjusted R Square) prend en compte le nombre de VI et le nombre d'observations. Il permet de comparer le pouvoir explicatif des modèles construits sur des échantillons de taille différente et/ou avec un nombre de VI diffèrent.
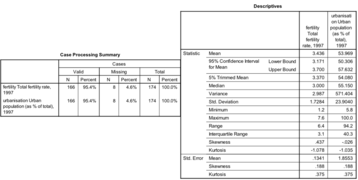
L’erreur moyenne de prédiction (Std. Error of the Estimate) indique que les pays s’écartent en moyenne de 1.38 unités de la VD de la droite de régression si on utilise le pourcentage de population urbaine pour expliquer le taux de fertilité. C’est une sorte de moyenne des résidus.
Lorsque l’on procède à une régression linéaire ou à une corrélation, on postule une relation linéaire. On doit s’assurer que ce postulat soit respecté. Bien que de nombreux phénomènes sociaux, économiques et politiques se résument par une relation linaire, toutes les relations ne sont pas linéaires.
Si on a une relation non-linéaire, il est possible de transformer des données de façon à ce qu’elles soient linéaires.
Pour modéliser une relation qui n’est pas linéaire mais curvilinéaire, on prend la variable dépendante et on l’élève au carré. On voit que Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑅^2} a augmenté passant de 26% à 36%.
Une autre manière est de transformer la variable indépendante en prenant le logarithme de la variable indépendance.
Sur un diagramme de dispersion, on peut parfois distinguer des valeurs extrêmes qui sont des observations qui s’écartent fortement des autres. Que doit-on faire lorsque l’on a des valeurs extrêmes ? Il faut relancer l’analyse de régression en excluant ces observations extrêmes (ou aberrantes) et voir si la pente, la constante et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑅^2} changent. Si c’est le cas, il existe deux solutions :
- les exclure des analyses avec l’inconvénient de diminuer notre échantillon et de perdre de l’information ;
- utiliser d’autres techniques statistiques que la régression par les moindres carrés comme la régression robuste qui est relativement insensible aux larges déviations dues à certaines observations aberrantes.
Les résidus sont l’erreur du modèle. On aimerait que les résidus soient :
- non-biaisés : c’est-à-dire avec une valeur moyenne de zéro pour chaque valeur ou intervalle
de valeur de la VI ;
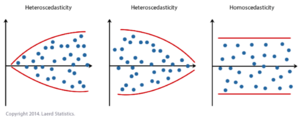
- homoscédastique (qui signifie « même tronçon ») : la dispersion des résidus devrait être la
même pour chaque valeur de la VI. Autrement dit, la variance autour de la droite de régression est constante. Les résidus sont hétéroscédastiques s’ils ne sont pas homoscédastiques.
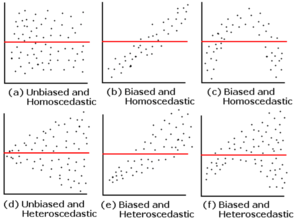
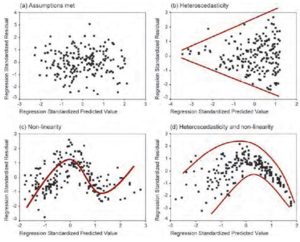
Sur le graphique A, les résultats sont non-biaisés et homoscédastique. Le graphique C est biaisé est homoscédastique, c’est-à-dire que l’écart des résidus est constant pour toute valeur de la variable indépendante.
L’hétéroscédasticité est l’augmentation (ou diminution) graduelle de la variance (visuellement présentée comme la distance de chaque observation par rapport à la droite de régression).
L’homoscédasticité est lorsqu’il n’y a pas de changements de la variance (les résidus ont la même variance, pas de structure de type « entonnoir »).
L’homoscédasticité des termes d’erreur (résidus), c’est-à- dire la variation constante des résidus par rapport à la droite de régression est un postulat de la régression linéaire à vérifier.
Les données agrégées sont des données obtenues en agrégeant (regroupant) des données individuelles pour une variable donnée et donc on change d’unité d’observation (pays, canton, entreprise, etc.). Il faut toujours être attentif à l’unité d’observation sur laquelle on travail.
On s’expose au risque d’erreur écologique lorsque, dans l'interprétation de données statistiques, on se fonde sur des données agrégées pour en inférer des conclusions sur des comportements individuels.
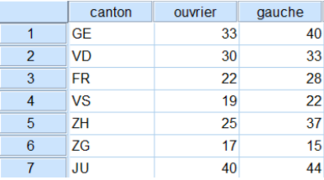
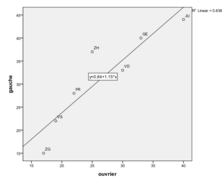
On d’intéresse à la relation entre le pourcentage d’ouvriers et le pourcentage de vote pour la gauche.
D’après ces données fictives, pour Genève on a un pourcentage d’ouvrier de 33% et un taux de vote en pourcentage pour la gauche de 40%. Avec la variable indépendante qui est le pourcentage d’ouvrier qui tente d’expliquer le vote pour les partis de gauche, on conclut qu’il y a une relation très positive. Au niveau des cantons, plus le niveau de pourcentage d’ouvrier est élevé, plus le niveau de pourcentage de vote pour la gauche est élevé. Au niveau agrégé (les cantons suisses), l’analyse montre que les cantons qui ont le plus fort pourcentage d’ouvriers présente le plus fort pourcentage de vote pour la gauche. Plus le pourcentage d’ouvriers augmente, plus le pourcentage de vote pour la gauche augmente
Peut-on en conclure pour autant que les ouvriers votent davantage pour la gauche que les non ouvriers ? Non. Ce serait une conclusion erronée, une erreur écologique, car des analyses au niveau individuel montrent que les ouvriers votent moins pour la gauche que les non ouvriers et que les ouvriers votent davantage pour l’UDC que les non-ouvriers (réalignement du vote de classe). Il est possible, bien que peu probable, que tous les ouvriers aient voté pour la droite ou l’extrême droite. Et que ce sont les 67% de non ouvriers qui aient voté pour la gauche. Dans ce cas, au niveau individuel, les ouvriers votent davantage pour la droite que les non ouvriers (et même exclusivement). En d’autres termes, l’erreur a été ici de considérer que tous les individus du groupe (ici le canton) pour lequel la valeur agrégée est calculée possèdent les caractéristiques du groupe en général.
Des hypothèses formulées au niveau individuel doivent être vérifiées au niveau individuel (c’est-à-dire avec des données dont l’unité d’analyse est l’individu). Au niveau agrégé, on enregistre des moyennes qui masquent des variations « intra- ». Par exemple, les pourcentages cantonaux masquent les variations communales. Ces dernières masquent les variations dans les quartiers et celles-ci masquent les variations individuelles.
Inférence statistique[modifier | modifier le wikicode]
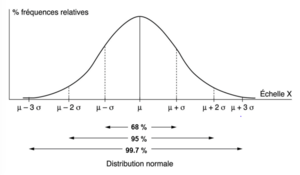
Généralement, une inférence statistique est une distribution symétrique et qui se présente sous forme de cloche. Pour être considérée comme une distribution normale, la distribution doit respecter la formule suivante :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌 = \frac {e^{\frac{-(x - 𝝁)^2}{2σ^2}}}{σ \sqrt {2𝜋}}}
Ce qu’il faut retenir de cette formule est que les distributions normales ne dépendent que de la moyenne Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝝁} et de l’écart-type Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝝈} , les autres termes (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑒} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝜋} ) sont des constantes.
Il existe un nombre infini de distributions normales, une pour chaque combinaison possible d’une moyenne et d’un l’écart-type. Une distribution normale avec une moyenne de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝜇} et un écart-type de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝝈} est noté Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑵(𝝁, 𝝈)} . Par exemple, dans un échantillon, la taille moyenne est de 172cm avec un écart-type de 17cm. Ces tailles forment une distribution normale notée Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑁(172, 17)} .
Quand la courbe passe de concave à convexe, on se situe à un écart-type de la moyenne. Même des variables qui n’ont pas une distribution normale peuvent produire des données qui sont distribuées normalement.
Lorsqu’on calcul un pourcentage ou un coefficient au sein d’un échantillon, on obtient une estimation d’un paramètre de la population.
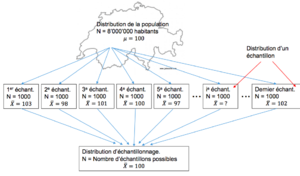
Imaginons qu’on connaisse la moyenne du QI au sein de la population Suisse. Il y a 8 millions d’habitant et on sait que cette moyenne est égale à 100. En général on ne connait pas le paramètre de la population et on cherche à l’estimer avec des échantillons.
On tire un échantillon représentatif de 2000 personnes qui permet d’obtenir une moyenne de 70, on tire un autre échantillon et la moyenne est de 98, un troisième avec une moyenne de 130. Quand la courbe passe de concave à convexe, on se situe à un écart-type de la moyenne. Même des variables qui n’ont pas une distribution normale peuvent produire des données qui sont distribuées normalement.
Lorsqu’on calcul un pourcentage ou un coefficient au sein d’un échantillon, on obtient une estimation d’un paramètre de la population.
Il existe des milliards d’échantillon possible et chacun va représenter un propre distribution des QI est une propre moyenne des QI. De ce point de vue, un paramètre particulier de la population comme par exemple la moyenne de QI a de nombreux estimateurs possibles qui sont la moyenne de QI des échantillons qu’on pourrait tirer. Comme l’échantillon se fait de manière aléatoire, on ne peut jamais savoir comment se présentera un échantillon avant d’en avoir analysé le score.
Supposons qu’on calcul la moyenne de ces milliards d’échantillons et on en dresse la distribution. On obtiendrait une distribution d’échantillonnage et on obtiendra la valeur qu’on observe au sein de la population qui serait de 100.
La distribution d’échantillonnage est la distribution d’une statistique quelconque, comme une proportion, une moyenne, etc., de tous les échantillons possibles d’une taille donnée. La distribution d’échantillonnage de la moyenne est assez semblable à une distribution normale (quelle que soit la forme que prend, au sein de la population, la distribution de la variable) :
- la moyenne de toutes les moyennes d’échantillons possibles sera identique à celle de la population ;
- l’écart-type de la distribution des moyennes de tous les échantillons possibles vaudra Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {𝝈}{\sqrt {N}}} .
L’écart-type d’une distribution d’échantillonnage des moyennes de tous les échantillons d’une taille précise qu’il est possible d’extraire aléatoirement d’une population a un nom particulier est appelé l’erreur-type ou l’erreur standard.
L’erreur standard est un indicateur de la variabilité de l’estimation (moyenne, proportion, corrélation, coefficient, etc.) entre échantillons. Formellement : l’erreur standard est l’estimation de l’écart-type de l’estimateur utilisé. L’erreur standard est calculée à partir de l’échantillon. Pour un paramètre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝜃} (qui peut être une moyenne, une proportion, une corrélation, un coefficient, etc.), on la note Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat{𝜎_𝜃}} .
Soit une moyenne Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝜇} d’une population que l’on estime avec la moyenne Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋} dans l’échantillon. L’erreur standard de la moyenne d’échantillon :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {𝜎_\bar {x}} = \frac {S}{\sqrt {n - 1}}}
Par exemple, si on s’intéresse à l’âge des personnes résidant en Suisse en 2008. L’âge moyen 𝑋 des Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑛 = 1819} individus est de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 48.59} ans avec un écart-type de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 18.344} . On en déduit l’erreur standard :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {𝜎_\bar {x}} = \frac {18.344}{\sqrt {1819 - 1}} = 0.430}
La variabilité est ici faible en raison, notamment, de la taille importante de l’échantillon. Plus l’échantillon est grand et plus l’erreur standard sera petite.
Soit une proportion 𝑝 d’une population que l’on estime avec la proportion 𝑝 dans l’échantillon. Son erreur standard est :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {𝜎_\hat {x}} = \sqrt {\frac {\hat {p}(1 - \hat {p})}{n - 1}}}
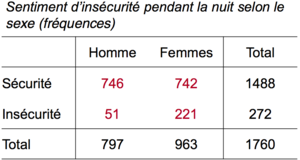
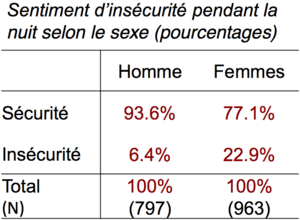
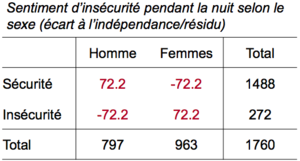
Par exemple, la proportion de femmes résidentes en Suisse en 2008 se sentant en insécurité pendant la nuit. La proportion observée est 𝑝 = 0. 229 = 22.9% parmi les Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑛 = 963} femmes concernées. On en déduit l’erreur standard :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {𝜎_\hat {x}} = \sqrt {\frac {0.229(1 - 0.229)}{963 - 1}} = 0.014}
Lors de l’estimation d’un paramètre (moyenne, proportion, coefficient, ...), on appelle marge d’erreur la demi-longueur de l’intervalle de confiance à 95%. C’est approximativement : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 2 \times \hat{𝜎}_{\hat{𝜃}}} à savoir 2 fois l’erreur standard.
Ainsi, 𝒆𝒔𝒕𝒊𝒎𝒂𝒕𝒊𝒐𝒏 ± 𝒎𝒂𝒓𝒈𝒆 𝒅′𝒆𝒓𝒓𝒆𝒖𝒓 définit approximativement un intervalle de confiance à 95%. Reprenons le cas de l’âge des personnes résidant en Suisse en 2008, dont la moyenne est 48.59. On a trouvé une erreur standard de 0.430. La marge d’erreur est donc de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 2 \times 0.430 = 0.86} .
L’intervalle de confiance à 95% de la moyenne μ de la population est approximativement :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝜇 = 48.59 ± 0.86}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝜇 ∈ [47.73, 49.45]}
C’est une forme d’inférence descriptive ou on a inféré la population suisse avec un certain échantillon. Avec cet échantillon, on accepte de se tromper à 5%.
La proportion de femmes en insécurité est Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat{𝑝} = 0.229} = 22.9%, avec une erreur standard de 0.014. La marge d’erreur est donc Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 2 \times 0.014 = 0.028} , ce qui donne comme intervalle de confiance à 95% :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑝 = 22.9\% ± 2.8\%}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑝 ∈ [20.1\%, 25.7\%]}
Pour les hommes en insécurité, on a : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat{𝑝} = 0. 064} = 6.4%, avec une erreur standard de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.009} et donc une marge d’erreur de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.017} :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑝 = 6.4\% ± 1.7\%}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑝 ∈ [4.7\%, 8.1\%]}
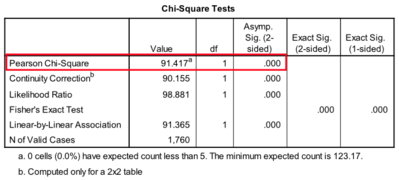
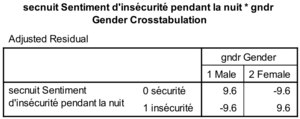
Les intervalles ne se recoupent pas, donc la différence d’insécurité entre hommes et femmes est significative.
Un résultat statistique observé au sein d’un échantillon, comme :
- différence entre une valeur observée dans l’échantillon et une valeur de référence
(qui dépend de l’hypothèse formulée) comme une moyenne d’âge inferieur à 50 ans ou un coefficient de régression différent de 0 (c’est-à-dire que la VI exerce un effet positif ou négatif) ;
- différence entre deux valeurs qui est soit une différence entre proportions d’hommes et de femmes en insécurité, soit une différence de l’âge moyen entre les abstentionnistes et les votants.
Est-il statistiquement significatif, c’est-à-dire qu’il ne provient pas du hasard ou des fluctuations de l’échantillonnage ?
L’objectif d’une analyse statistique de données d’échantillon est de tirer des conclusions par rapport à la population. Il s’agit d’inférer les caractéristiques de la population à partir de l’échantillon. Des différences entre des pourcentages ou entre des moyennes au sein d’un échantillon peuvent refléter des différences réelles, c’est-à-dire des différences au sein de la population ou être dues au hasard, c’est-à-dire résulter des fluctuations d’échantillonnage (un autre échantillon pouvant donner des différences de pourcentages ou de moyennes différentes, ou même nulles).
Les tests de signification statistique permettent de déterminer la probabilité que les différences observées au sein d’un échantillon soient dues au hasard (c’est-à-dire aux fluctuations d’échantillonnage) et non à des différences réelles dans la population. On cherche à déterminer la probabilité de découvrir une relation dans notre échantillon quand il n’y en a pas dans notre population. Si cette probabilité est petite, on peut conclure qu’il existe une relation dans la population. L’usage est de considérer qu’une probabilité petite est une probabilité de 1 sur 20 ou moins, c’est-à-dire Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑝 < 0.05} .
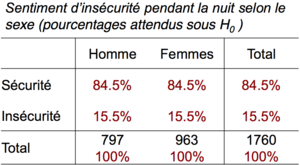
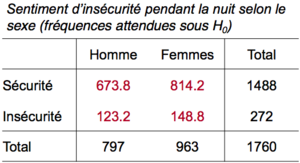
Les étapes d’un test de signification appelé aussi un test d’hypothèse sont :
- Formulation d’une hypothèse Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑯_𝟏} (les différences ne sont pas dues au hasard) et d’une hypothèse nulle Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑯_𝟎} (les différences sont dues au hasard). L’hypothèse Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_1} est l’hypothèse de recherche qui prévoit une relation entre deux variables ou un effet d’une variable sur une autre. L’hypothèse nulle (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_0} ) affirme l’absence de relation dans la population à savoir qu’« il au hasard) ». Quand on teste un coefficient de corrélation ou de régression, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_0} prévoit généralement que le coefficient est égal à zéro ce qui indique une absence d’effet de la VI. Dans un test statistique, il s’agit de déterminer si on peut rejeter l’hypothèse nulle (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_0} ) et donc accepter l’hypothèse alternative Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_1} , tout en indiquant le risque (la probabilité d’erreur) de se tromper.
- Fixer un seuil de signification (niveau de confiance) qui permet décider entre garder l’hypothèse nulle et la rejeter. Habituellement, par convention, les chercheurs en sciences sociales retiennent un seuil de 0.05(5%), d’autres seuils usuels sont Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.01} (1%) ou Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.001} (0.1%). Un résultat statistique est statistiquement significatif s’il y a très peu de chances (en général < 𝟓%) qu’il soit dû au seul hasard de l’échantillonnage. Si les chances de trouver une relation dans l’échantillon alors qu’il n’y en a pas dans la population sont supérieures à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.05} (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} sur Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 20} ). La relation découverte au sein de l’échantillon doit peut-être son existence au hasard de l’échantillonnage. On ne peut pas rejeter Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_0} et on dit que la relation n’est pas significative. Si les chances de trouver une relation dans l’échantillon alors qu’il n’y en a pas dans la population sont inferieures à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.05} (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} sur Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 20} ), on peut avoir confiance dans la relation découverte au sein de l’échantillon. On rejette Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_0} . La relation est statistiquement significative.
- Calculer le test statistique approprié à l’outil utilisé (avec un tableau croisé, on utilise le test du chi-deux, avec un tableau de moyenne le test de F, etc.) et déterminer sa probabilité d’erreur (valeur Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} , Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p - value} , SPSS la note souvent Sig.). La probabilité d’erreur (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑝 − 𝑣𝑎𝑙𝑢𝑒} ) est la probabilité que le résultat soit dû au hasard de l’échantillonnage. L’interprétation de la Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑝 − 𝑣𝑎𝑙𝑢𝑒} est qu’on quantifie le risque pris en affirmant « il y a une différence » si en fait Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_0} n’est pas faux ou que c’est la probabilité d’obtenir un résultat aussi (ou plus) extrême que celui observé s’il n'y a pas de relation dans la population (si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_0} est vraie). Même s’il n’y a pas de relation au sein de la population, on pourrait malgré tout, du fait des fluctuations d’échantillonnage, trouver dans certains échantillons une relation. Le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒑 − 𝒗𝒂𝒍𝒖𝒆} indique la probabilité de trouver une relation dans un échantillon alors même qu’il n’y en a pas dans la population.
- Si cette probabilité d’erreur est inferieure au seuil de signification fixé au préalable (habituellement 𝟎.𝟎𝟓), Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_0} sera rejetée et on dira alors que la relation entre deux variables observée à partir des données d’échantillon est statistiquement significative, c’est- à-dire qu’on peut inférer les résultats obtenus à l’ensemble de la population. La significativité sont les règles : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑝 − 𝑣𝑎𝑙𝑢𝑒} . Si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑝 < 0.05} , la relation est significative et on rejette Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_0} . Si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑝 > 0.05} , la relation n’est pas significative et on ne peut pas rejeter Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_0} . Selon l’outil utilisé, une relation non significative peut indiquer une corrélation nulle, une valeur nulle du coefficient de régression, une indépendance entre deux variables, etc. Si on fixe un seuil de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.05} , il reste une probabilité de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.05} (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} chance sur Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 20} ) que cette relation soit quand- même due au hasard.
Le test de F permet de tester la significativité statistique d’un modèle de régression, plus précisément la relation globale entre l’ensemble des variables de notre modèle (ensemble du modèle). On vérifie si le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑅^2} est significatif avec la probabilité d’erreur du test de F (Sig.).
Le test t de Student teste la significativité statistique d’un coefficient dans le cadre d’une régression linéaire (une variable à la fois). Il teste la nullité d'un coefficient de régression (𝛽). On vérifie si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝛽} est significativement diffèrent de zéro avec la probabilité d’erreur du test t de Student. L’hypothèse nulle (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_0} ) énonce que Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋} n’est pas lié à 𝑌 et donc que la pente Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝛽} (coefficient de régression) est égale à zéro dans la population. L’hypothèse alternative (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_1} ), qui devrait correspondre à votre hypothèse de recherche, énonce que Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} sont statistiquement associés et que la pente Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝛽} n’est pas égale à zéro dans la population :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_0 ∶ 𝛽 = 0}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_1 ∶ 𝛽 ≠ 0}
Un résultat statistiquement significatif n’est pas nécessairement un résultat réellement significatif par rapport à la question analysée. Une relation est réellement significative, dans le sens substantiel, seulement si elle est passablement forte.
La significativité statistique dépend aussi de l’effectif sur lequel est réalisée l’analyse. Avec un Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑵} grand, une très faible relation au point d’être sans intérêt sera statistiquement significative. Avec un Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑵} petit, une forte relation ne sera pas significative.
Sur la base de 10 observations, il y a une variable indépendante et on va tester l’hypothèse qu’elle exerce un effet sur la variable dépendante. Le test de F et le test de T donne le même résultat qui est supérieur au résultat qu’on a fixé. Le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑅^2} est de 0.25, soit 25% qui est expliqué par la variable dépendante. Il faut être attentif à la taille de l’effectif.
Introduction aux relations multivariées[modifier | modifier le wikicode]
Il y a six questions à soulever quand on analyse une relation :
- 1) Existe-t-il une relation entre les deux variables pour les données que nous analysons ?
- 2) Quelle est la force ou l’intensité de cette relation ?
- 3) Quelles sont la direction et la forme de la relation ?
- 4) Si une relation existe et si on travaille avec des données d’échantillon, peut- on généraliser la relation à la population de laquelle est tiré l’échantillon ?
Quand on analyse des variables d’intervalles, on utilise le diagramme de dispersion, les coefficients de régression, le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑟} , le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑅^2} et les tests de signification statistique.
- 5) La relation est-elle véritablement causale ? Ou n’est-elle pas plutôt une relation fallacieuse engendrée par une quelconque tierce variable ?
- 6) Quelles sont les variables intermédiaires qui relient la VI et la VD ?
Pour établir une relation causale entre deux variables, on doit introduire une ou plusieurs variables supplémentaires dans l’analyse.
| Expérimentation | Analyse multivariée |
|---|---|
| Le chercheur détermine aléatoirement (au hasard) quels sujets feront partie du groupe expérimental et lesquels feront partie du groupe de contrôle.
Le groupe expérimental et le groupe de contrôle seront équivalents ou presque quant à toutes les variables qui pourraient influencer la relation entre la VI et la VD.
Plus l’effectif de sujets est important, plus le groupe expérimental et le groupe de contrôle seront parfaitement équivalents.
Une fois que la VI est introduite dans l’expérimentation, les différences que le chercheur observe dans la VD entre le groupe expérimental et le groupe de contrôle ne pourront être attribuées à une autre variable que la VI. |
L’utilisation de variables de contrôle remplace l’assignation aléatoire des sujets au groupe expérimental et au groupe de contrôle.
L’introduction d’une variable de contrôle (VC) élimine l’effet de cette variable sur la relation entre la VI et la VD. L’analyse multivariée procède beaucoup plus lentement en contrôlant l’effet des autres variables à tour de rôle, ou au mieux quelques-unes à la fois.
Limites des fichiers de données en termes de variables. D’ailleurs, il se peut qu’on ne sache pas quelle est la VC appropriée. À l’aide des théories, on essaie d’inclure autant de VC plausibles et disponibles dans notre fichier de données. On doit accepter l’impossibilité de contrôler les effets de toutes les VC possibles. |
La causalité est centrale dans la démarche scientifique. Comment peut-on déterminer s’il existe une relation causale entre deux variables ?
Une relation causale est habituellement asymétrique avec une variable qui influence une autre : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋→𝑌}
Si on pense qu’une variable est la cause d’une autre, il faut que trois conditions soient remplies :
- une association entre les variables Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} ;
- une séquence temporelle appropriée ;
- il faut éliminer les explications alternatives.
Si une des trois conditions n’est pas remplie, on ne peut pas conclure à une relation causale. Les variables Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒀} doivent être corrélées. Les différentes techniques d’analyse bivariée visent à vérifier cette condition de la causalité comme la régression, la corrélation, l’analyse de tableau croisé, l’analyse de variance, etc. Ces techniques permettent de déterminer si les variables 𝑋 et 𝑌 sont associées. Par exemple, un diagramme de dispersion, un coefficient de corrélation ou de régression permet d’établir un tel diagnostic d’association entre deux variables d’intervalles
La VI doit se produire avant la VD : la cause doit précéder l’effet. Parfois c’est simplement une question de logique comme par exemple l’âge ou le sexe d’une personne qui est antérieur à ses attitudes.
La direction causale peut être moins évidente. Le fait de faire du scoutisme (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑆} ) peut réduire la tendance à la délinquance Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle (𝐷): 𝑆 → 𝐷} . Il est aussi possible que les jeunes délinquants évitent le scoutisme mais non pas les non-délinquants : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐷 → 𝑆} . L’ordre temporel n’est pas clair et les deux possibilités sont plausibles car Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑆 → 𝐷} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐷 → 𝑆} .
L’ordonnancement temporel n’est pas un problème statistique, c’est un problème de l’ordre de la théorie ou de la méthode de recherche. Notre théorie peut soutenir que les variables sont ordonnées d’une manière particulière.
Si deux variables sont associées et ont une séquence temporelle satisfaisant une relation causale, c’est encore insuffisant pour signifier une causalité. Il pourrait y avoir une explication alternative pour cette association. L’association entre les variables Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒀} ne doit pas être due à une troisième variable Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒁} ou à un ensemble de variables additionnelles. Par exemple, il se pourrait qu’une variable Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑍} cause à la fois Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} . Dans ce cas, la relation entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒀} est fallacieuse. Une explication alternative pour une association est responsable du rejet de beaucoup d’hypothèses portant sur une relation causale. Dans des études médicales, on a trouvé une association entre la quantité de café bu et la probabilité d’avoir une attaque cardiaque. Dès le moment où on prend en compte d’autres variables associé a la quantité de café bu tel que le pays de résidence ou la profession, le niveau de stress, cette association initiale entre la quantité de café bu et la probabilité d’avoir une attaque s’est fortement affaiblie voir à même complètement disparue. Cette condition pour la causalité d’éliminer les explications alternatives est la plus difficile à atteindre.
L’association entre le fait de fumer et le cancer du poumon est considéré généralement comme ayant un lien de causalité. L’association est modérément forte, il y a une séquence temporelle (le cancer vient après avoir fumé) et aucunes explications alternatives ont été trouvées pour expliquer la relation. De plus, le lien causal a été renforcé par des théories biologiques qui expliquent comment la fumée cause un cancer du poumon. Parfois on peut entendre quelqu’un qui donne une preuve anecdotique tentant de réfuter cette relation causale comme par exemple, « mon grand-père a 90 ans, il fume deux paquets de cigarettes par jour et il est encore en très bonne santé ». Une association n’a pas besoin d’être parfaite pour être causale. Pas toutes les personnes qui fument deux paquets de cigarettes par jour auront un cancer du poumon. Un plus grand pourcentage de ces fumeurs aura un cancer que les non-fumeurs. Une preuve anecdotique n’est pas suffisante pour réfuter une relation causale sauf si elle remet en question une des trois conditions de la causalité.
En fin de compte, on ne peut jamais prouver qu’une variable est la cause d’une autre. On peut réfuter des hypothèses causales en montrant que des évidences empiriques contredisent au moins une de ces trois conditions mais on ne peut pas prouver une relation causale. On va essayer de prouver par les explications alternatives.
La composante principale pour évaluer si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿} pourrait causer Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒀} est dans la recherche pour une explication alternative. On examine si l’association entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} reste après avoir contrôlé les effets des autres variables sur cette relation. Avec des données individuelles la classe sociale, l’éducation, le revenu, l’âge et le sexe sont des variables de contrôle souvent utilisées. Par exemple, pour contrôler par le niveau d’éducation une relation causale, on pourrait diviser l’échantillon selon les différents niveaux de formation et on regarde si à l’intérieur de chacun des niveaux de formation on observe la même relation causale.
Ce diagramme de dispersion est un exemple de contrôle par le niveau scolaire : on se pose la question de savoir si les étudiant de grande taille sont meilleur que les petits étudiants en mathématique. La corrélation pourrait être par exemple de 0,8 entre la taille des élèves et leurs notes en mathématique signifiant qu’il y a une relation positive : les grands étudiants ont des notes élevé en mathématique à l’inverse des petits étudiants.
On se pose la question de savoir si la taille influence les notes en mathématique. Une explication alternative pour cette observation est que cette échantillon comporte des étudiants d’un niveau scolaire différent et donc d’âge scolaire différent. Donc, quand le niveau scolaire augmente, la taille et le résultat en mathématique augmente étant donné que plus on monte en niveau scolaire et plus on est grand parce qu’on prend de l’âge. On peut éliminer les effets du niveau scolaire sur cette association par un contrôle statistique qui étudie la progression entre la taille et la note en mathématique pour des étudiant d’un niveau scolaire identique. À ce moment, on dit qu’on a contrôlé pour un niveau d’éducation en analysant la relation à chaque niveau scolaire séparément.
Dans ce graphique, les chiffres représentent des étudiants, on a tracé la droite de régression en bleu, on voit une relation positive bivariée initiale. Sur l’axe Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋} c’est la taille, et l’axe Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} est la note en mathématique qu’on cherche à expliquer. Si on prend en compte la taille des étudiants d’un district donné, on aurait une relation positive : plus la taille augmente, plus la note en mathématique augmente. On a distingué chacun des individus selon son niveau scolaire, 2 indiquerait un bas niveau scolaire, 5 un niveau scolaire intermédiaire et 6 un plus haut niveau scalaire. Après, pour chacun de ces niveaux scolaires on a tracé un droit de régression qui sont les trois droite en rouge correspondant à la relation entre la note obtenue en mathématique et la taille des élèves. On voit que les trois droites sont plates indiquant l’absence de relation entre la note et la taille. Quand elle est plate, cela veut dire que quelque soit la taille des élèves, la note en mathématique est similaire. De ce point de vue, après avoir contrôlé la relation entre la relation initiale est la note obtenue en mathématique, on peut dire que la relation initiale est fallacieuse, la relation disparaît lorsqu’on a introduit la variable « niveau scolaire ». on pourrait remplacer la variable « niveau scolaire » par la variable « âge » et on obtiendrait exactement le même résultat.
En résumé, on contrôle par une variable en tenant ces valeurs constantes, c’est-à-dire qu’on va contrôler si la relation existe pour chaque valeur de la variable de contrôle. En tenant constant la variable de contrôle, on élimine l’influence de cette variable sur l’association Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle X} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Y} . si la relation disparait, on a à faire à une relation causale fallacieuse. Si elle persisterait, on aurait contrôlé par le niveau scolaire et on pourrait dire qu’à ce stade, il y a une relation de causalité. On devrait contrôler par d’autres variables également et par d’autres explications alternatives. Pour chacune des droites en rouge correspondant à trois régressions, le coefficient de corrélation est de 0, il n’indique pas de relations.
Il n’est pas évident de savoir quelles variables doivent être utilisées comme des variables de contrôle (VC). La théorie et les travaux dans le domaine aident en général le chercheur à savoir quelles variables doivent être utilisées comme VC. Un potentiel piège de presque toute les recherche en sciences sociales est qu’une important variable n’a pas été inclue dans l’étude. Si on ne contrôle par cette variable qui influence fortement la relation entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒀} , les résultats seront erronés. Cette variable non mesurée dans une étude ou inconnue des chercheurs mais qui influence l’association est parfois appelée variable cachée.
Il existe plusieurs types de relations multivariées qui s’observent dans la recherche en sciences sociales :
- la relation fallacieuse ;
- la chaîne de relations causales ;
- les causes multiples : causes indépendantes ;
- les causes multiples : effets directs et indirects ;
- l’interaction statistique ;
- la variable dissimulatrice.
relation fallacieuse[modifier | modifier le wikicode]
Une association entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_1} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒀} est dite fallacieuse si les deux variables sont dépendantes d’une troisième variable Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_𝟐} et si leur association disparaît quand on a contrôlé par Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_𝟐} . Dans ce cas, l’hypothèse d’une relation causale entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_𝟏} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒀} est réfutée.
chaîne de relations causales[modifier | modifier le wikicode]
La relation fallacieuse n’est pas le seul type pour lequel l’association entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_1} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Y} disparaît lorsqu’on contrôle pour une troisième variable, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_2} . Un autre cas de figure est la chaîne de relation de causalité dans laquelle Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_𝟏} affecte Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_𝟐} qui à son tour affecte Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒀} . Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_1} est une cause indirecte de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} , plutôt que directe et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_2} est une variable intermédiaire. En termes de temporalité, la variable intermédiaire 𝑿𝟐doit apparaître après Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_𝟏} et avant Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒀} dans la chaîne causale.
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_1 → 𝑋_2 → 𝑌}
Par exemple, les études sur la longévité humaine montre qu’elle est associée à un niveau d’étude élevé. Certains chercheurs considèrent que l’éducation est la variable la plus importante pour expliquer la durée de vie d’une personne. Est-ce que c’est véritablement le fait d’avoir plus d’éducation qui favorise une longue vie ? À ce stade, établir une relation causale est difficile est beaucoup de chercheurs pensent qu’il y a une relation en chaine avec peut être le revenu comme variable intermédiaire. Pour de nombreuses raisons, le revenu favorise une longue vie. Dans ce schéma, le revenu joue un rôle de variable intermédiaire. Dans ce cas, l’éducation est une cause indirecte de la longue à travers le revenu et ce qu’on observe dans une chaine causale ou dans un relation fallacieuse, l’association entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} disparait lorsqu’on contrôle pour une troisième variable. Au niveau des tests statistiques, on obtient les mêmes résultats.
causes multiples : causes indépendantes[modifier | modifier le wikicode]
En sciences sociales, les VD ont presque toujours plus qu’une cause. Par exemple, un ensemble de facteurs ont probablement un effet causal sur la délinquance juvénile ou sur une vie longue. Les VI qui causent Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Y} sont statistiquement indépendantes. Par exemple, le sexe et l’origine ethnique sont deux VI qui sont statistiquement indépendantes.
Ce schéma représente Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_1} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_2} qui influencent Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} .en d’autres termes, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_1} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_2} sont des causes séparées de 𝑌 et on dit que 𝑌 à des causes multiples. Parfois les variables indépendantes qui causent 𝑌 sont statistiquement indépendantes.
Causes multiples : effets directs et indirects[modifier | modifier le wikicode]
En sciences sociales, la plupart des VI sont associées. En raison des liens complexes d’association, quand on contrôle par une variable Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_𝟐} ou par un ensemble de variables Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_𝟐} , Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_𝟑} , ..., la relation entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_𝟏} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒀} peut changer. Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_1} peut avoir un effet direct sur Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} et aussi des effets indirects à travers les autres variables. Dès lors qu’on introduit une variable indépendante, la relation initiale devrait changer. La plupart des phénomène qu’on observe en science sociale on des causes qui sont directes et indirectes.
On pourrait voir un fort effet du fait que d’être issu d’une famille monoparentale engendre de la délinquance. On introduit comme variable de contrôle la pauvreté et on verrait une diminution de la relation entre famille monoparental et délinquance mais il y a aurait toujours un effet qui persisterait.
Par exemple, ce serait le fait d’être une famille monoparentale qui favorise la pauvreté. Lorsque des couples divorces, cela créé une diminution des revenu autant chez le père que la mère mais notamment celui qui a la charge de l’enfant. Dans ce cas, provenir d’une famille monoparentale peut avoir un effet direct sur la délinquance. Mais provenir d’une famille monoparentale peut produire des effets indirects notamment être pauvre.
Interaction statistique[modifier | modifier le wikicode]
Quand l’effet de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_𝟏} sur Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Y} change aux différents niveaux de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_𝟐} , la relation présente une interaction statistique. Quand l’effet de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle X} sur Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Y} change pour différent niveau de la variable de contrôle, la relation présente une interaction statistique. Pour évaluer s’il y a une interaction, comparer l’effet de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_1} sur Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} aux différents niveaux de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_2} . Si l’effet est similaire à chaque niveau de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_2} , il n’y a pas d’interaction. L’interaction existe quand la variabilité des effets est grande.
Par exemple, la relation peut être positive à un niveau de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_2} et négative à un autre, ou forte à un niveau et faible ou inexistante à un autre. Quand on a à faire à une interaction, on dit que Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_𝟐} affecte la relation entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑿_𝟏} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒀} .
Par exemple, la relation entre le revenu annuel en milliers de dollars (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} ) et le nombre d’années d’études (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_1} ) selon le sexe (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_2} ). Si on suppose que l’équation de régression est :
- pour les hommes : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑦 = −10 + 4𝑥_1}
- pour les femmes : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑦 = −5 + 2𝑥_1}
En moyenne, le revenu pour les hommes augmente de 4000$ pour chaque année d’éducation, alors que pour les femmes, il augmente de 2000$ par année d’éducation. L’effet de l’éducation sur le revenu varie selon le sexe, avec un effet plus fort pour les hommes que pour les femmes. Il y a une interaction entre l’éducation et le sexe dans leurs effets sur le revenu. En l’absence d’un effet d’interaction entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_1} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_2} , cela ne signifie pas que Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_1} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_2} ne soient pas associés.
Variable dissimulatrice[modifier | modifier le wikicode]
Occasionnellement, deux variables peuvent n’avoir aucune relation au niveau bivarié (la relation bivariée est nulle), jusqu’à ce que l’on introduise une troisième variable qui met en exergue une relation. Dans ce cas, la variable de contrôle révèle une relation entre deux variables. Cette variable de contrôle est appelée variable dissimulatrice. Si par exemple on s’attendait à trouver une relation bivariée entre les données parce que la théorie le dit ou parce que l’expérience le suggérait, alors il faudrait peut être penser à une variable dissimulatrice.
Ces exemples ne sont pas exhaustifs. Il existe d’autres possibles structures d’association. Il est même possible qu’une relation bivariée montre une relation positive et qu’après avoir contrôlé par une variable, chaque relation aux différents niveaux de la VC présente une relation négative. Les choses sont souvent un petit peu plus nuancées et moins nettes (plus complexes) dans la réalité sociale, car elle est un réseau imbriqué de relations causales. Dans la réalité sociale, sont plus complexes.
Régression linéaire multiple[modifier | modifier le wikicode]
La régression linéaire multiple est un prolongement de la régression linéaire simple. Elle est une technique statistique qui cherche à modéliser l’effet de plusieurs VI (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_1, 𝑋_2, 𝑋_3, ...} ) sur la VD (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Y} ). Elle permet de tester des relations causales dans lesquelles on fait l’hypothèse qu’une (ou plusieurs) VI affecte(nt) une VD.
La relation entre plusieurs variables d’intervalles peut s’écrire de la manière suivante :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌_i = 𝑏_0 + 𝑏_1𝑋_{1i} + 𝑏_2𝑋_{2i} + 𝑏_3𝑋_{3i} + 𝑒_i}
L’équation de régression multiple prend la forme algébrique suivante :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {𝑌} = 𝑏_0 + 𝑏_1𝑋_{1i} + 𝑏_2𝑋_{2i} + 𝑏_3𝑋_{3i}}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} = valeur estimée de la VD par le modèle
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑏_0} = constante (valeur de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑌} quand Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_1 = 𝑋_2 = 𝑋_3 = 0} )
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑏_1} = le coefficient de variable indépendante Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_1}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑏_2} = le coefficient de régression pour la variable indépendante Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_2}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑏_3} = le coefficient de régression pour la variable indépendante Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑋_3}
Par exemple, on cherche à expliquer le conservatisme des individus. L’hypothèse est que le niveau individuel de conservatisme augmente avec la religiosité et l’auto-positionnement à droite, et diminue avec le niveau de formation. On peut résumer cette hypothèse sel on ce schéma théorique :
L’équation de régression du modèle est :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {𝑌} = 𝑏_0 + 𝑏_1\ 𝑟𝑒𝑙𝑖𝑔𝑖𝑜𝑠𝑖𝑡é + 𝑏_2\ 𝑎𝑢𝑡𝑜𝑝𝑜𝑠𝑖𝑡𝑖𝑜𝑛\ 𝑑𝑟𝑜𝑖𝑡𝑒 − 𝑏_3\ 𝑛𝑖𝑣𝑒𝑎𝑢\ 𝑓𝑜𝑟𝑚𝑎𝑡𝑖𝑜𝑛}
Pour tester la significativité statistique de la relation globale entre l’ensemble des variables de notre modèle, on vérifie si le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑹𝟐} est significatif avec la probabilité d’erreur du test de Fisher (Sig.). Dans cet exemple, il est significatif car la probabilité d’erreur est inférieure au seuil fixé par convention à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.05} (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p < 0.05} ). À ce stade, ce n’est pas parce que le test est significatif que toutes les variables exercent un effet significatif. Un modèle peut être significatif uniquement avec une seule variable alors qu’on a introduit trois variables. En général, dans un modèle de régression multiple ce qu’on regarde d’avantage est le test T.
La qualité du modèle est donnée par Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑹𝟐} (puissance explicative du modèle) et l’erreur standard d'estimation (Std. Error of the Estimate) sont à interpréter de la même manière que dans une régression simple. Le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑹𝟐} ajusté (Adjusted R Square) est utilisé pour comparer le pouvoir explicatif de modèles construits sur des échantillons de taille différente et/ou avec un nombre de VI diffèrent. Dans une régression multiple, on ne commente pas le coefficient de corrélation Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑟} .
La colonne « Sig. » du tableau Coefficients présente les probabilités d’erreur du test t de Student pour chaque coefficient non standardisé. Une probabilité d’erreur inférieure au seuil de signification choisi indique un effet statistiquement significatif de la VI. Par convention, on fixe le seuil de signification à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.05} . Dans ce tableau, toutes les VI ont un effet significatif sur le niveau de conservatisme : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑝 < 0.05} . on conclut que les trois variables indépendantes on un effet significatif sur le niveau de conservatisme.
Les intervalles de confiance permettent de déterminer avec un niveau de confiance de 95% la fourchette dans laquelle évoluent les coefficients non standardisés (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐵} ). Si la valeur Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} est inclue dans l’intervalle de confiance, l’effet de la variable indépendante sur Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Y} est non significatif (on ne peut pas rejeter Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝐻_0} ). Dans ce tableau, le coefficient non standardisé pour l’éducation mesurée en années varie entre −0.44 et −0.20 avec un niveau de confiance de 95%. Comme l’intervalle de confiance n’inclut pas le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝟎} , on peut rejeter Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑯_𝟎} et conclure que l’éducation exerce un effet significatif et négatif sur le niveau de conservatisme.
Les coefficients non standardisés permet de réécrire l’équation avec ces coefficient. Le modèle de régression multiple peut être résumée par l’équation :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {𝑌} = 𝑏_0 + 0.920\ 𝑟𝑒𝑙𝑖𝑔𝑖𝑜𝑠𝑖𝑡é\ + 0.964\ 𝑎𝑢𝑡𝑜𝑝𝑜𝑠𝑖𝑡𝑖𝑜𝑛\ 𝑑𝑟𝑜𝑖𝑡𝑒\ − 0.322\ 𝑛𝑖𝑣𝑒𝑎𝑢\ 𝑓𝑜𝑟𝑚𝑎𝑡𝑖𝑜𝑛}
Pour une augmentation de 1 année de formation, le niveau de conservatisme diminue de 0.322 point. Pour une augmentation de 1 point sur l’échelle de religiosité, le niveau de conservatisme augmente de 0.92 point. Pour une augmentation de 1 point sur l’échelle de positionnement gauche-droite, le niveau de conservatisme augmente de 0.964 point.
Les coefficients standardisés (Beta) prennent sens dans une régression multiple. Ce sont des coefficients qu’on a standardisés. Cela permet de comparer les coefficients entre eux, les coefficients qui on une unité de mesure différente. Ainsi, ils sont utilisés pour estimer la contribution relative de chaque VI à la variable dépendante et ils permettent de comparer l’effet des VI qui n’ont pas la même unité de mesure. La VI qui a le coefficient beta avec la valeur absolue la plus élevée est le coefficient qui a le plus de poids dans l’explication du conservatisme. Dans notre modèle explicatif, la variable ayant la contribution la plus importante sur le niveau de conservatisme est le niveau de religiosité.
On peut résumer notre modèle par ce graphique. Notre hypothèse est vérifiée. Le niveau individuel de conservatisme augmente avec la religiosité et l’auto-positionnement à droite, et diminue avec le niveau de formation. Si un variable n’exerce pas d’effet significatif, il ne faut pas l’insérer dans le modèle final.
La corrélation simple (Zero-order) correspond à la corrélation entre la VI et la VD (indépendamment des autres VI). La corrélation semi-partielle (Part) représente la part de variation commune entre une VI et une VD qui n’est partagée par aucune des autres VI.
Le carré de la corrélation semi-partielle (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑠𝑝^2} ) représente la proportion de la variation de la VD expliquée uniquement par la VI. Il indique contribution unique de la VI au Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑹^𝟐} .
Chaque cercle représente la variation d’une variable. Le cercle qui se chevauche indique qu’il y a une corrélation ou une variation commune entre les différentes variables. Par exemple, la variable Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle eduyrs} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle rlgdgr} ne se chevauchent pas. Si on examine les corrélations simples entre ces deux variables, elles ne sont pas liées. On a une surface et le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑅^2} indique la part de cette surface qu’on explique avec les autres variables. L’objectif est d’en expliquer un maximum.
Cette équation explique tout ce qui est expliqué par les trois variables indépendantes :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑅^2 = 𝑎 + 𝑏 + 𝑐 + 𝑑 + 𝑒}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑓 = 1 – 𝑅^2} (variation de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle ccon100} non expliquée par le modèle)
- Surface Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑎} = contribution unique de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle eduyrs} .
- Surface Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑒} = contribution unique de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle lrscale} .
- Surface Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑑} = contribution unique de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle rlgdgr} .
- Surface de chevauchement Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle b} = contribution conjointe/commune au Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑅^2} de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle eduyrs} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle lrscale} .
- Surface de chevauchement Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle c} = contribution conjointe/commune au Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑅^2} de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle lrscale} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle rlgdgr} .
Le carré de la corrélation semi-partielle pour Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle eduyrs} indique la proportion de variation de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle ccon100} uniquement expliquée par Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle eduyrs} .
La multicolinéarité constitue un problème dans un modèle de régression multiple. La multicolinéarité survient lorsque, dans un modèle de régression, deux ou plusieurs VI sont trop fortement corrélées entre elles. Il existe une relation linéaire parfaite ou presque parfaite entre deux ou plusieurs variables explicatives lorsque la colinéarité est très forte corrélation entre deux VI ou lorsque la multicolinéarité est très forte corrélation entre trois ou plus VI. La conséquence de la multicolinéarité est un problème d’estimation des paramètres du modèle (instabilité des coefficients estimés) et une forte variance des paramètres estimés, intervalles de confiance autour des paramètres importants, tests t de Student peu significatifs. Lorsqu’il y a de la multicolinéarité, tous les paramètres estimés peuvent être biaisés. Il faut toujours procéder à un diagnostic de multicolinéarité qui est indispensable.
Voici deux coefficients de multicolinéarité produits par SPSS. La tolérance est une coefficient qui varie de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} est Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} correspond à l’absence de multicolinéarité. C’est l’idée que pour un variable indépendante, cela correspond à la proportion de variance non partagée avec les autres variables indépendante.
Pour une VI, proportion de la variance non-partagée avec les autres VI, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑒𝑑𝑢𝑦𝑟𝑠 = 0.991} correspondant à la variation spécifique de la variable Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle eduyrs} . Seul 1% (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1 – 0.991 = 0.009} ) de la variance de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle eduyrs} est commune avec Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle lrscale} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle rlgdgr} . La tolérance est ce qu’on appel le complémentaire à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} du Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑅^2} de la régression de la variable indépendante par les autres variables intendantes. L’idée est que si la tolérance est faible ou très faible, il y a un risque de multicolinéarité et une des variables intendantes est redondantes et il faut réexaminer le rôle de la variable dans le modèle.
Le facteur d’inflation de la variance (VIF) est l’inverse de la tolérance soit Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle VIF = \frac {1}{tolérance}} . Si le VIF est de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} cela indique une absence de multicolinéarité.
Selon l’interprétation par la tolérance, une valeur proche de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1.0} signale l’absence de (multi)colinéarité, alors que des valeurs proches de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.0} signalent l’existence d’un problème de (multi)colinéarité.
Selon une interprétation du facteur d’inflation de la variance (VIF), une valeur proche de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1.0} signale l’absence de (multi)colinéarité, alors que des valeurs proches de l’infini signalent l’existence d’un problème de (multi)colinéarité.
Que faire en cas de multicolinéarité ? Il est possible de supprimer les variables qui causent problème, néanmoins, il y a un problème si cela concerne une variable centrale de votre modèle. On peut combiner les variables fortement corrélées (construction d’échelle) et revoir le modèle, si aucune solution n’est satisfaisante. La réflexion théorique est importante parce que c’est elle qui va indiquer quelle variable on va introduire dans le modèle et si on obtient des seuils qui indique que deux variables peuvent présenter des problèmes potentiels de multicolinéarité, il faut faire primer la réflexion théorique.
Corrélation et régression linéaire : les droits de l’homme[modifier | modifier le wikicode]
Dans un modèle de régression, on est censé utiliser des variables d’intervalles. Le problème est qu’en sciences-sociales, il y a beaucoup de variables catégorielles donc ordinales ou cardinales. Des variables catégorielles peuvent être introduites dans un modèle mais elles peuvent être introduites que sous la forme de variables dichotomiques. En d’autres termes, des variables dichotomiques peuvent être introduites dans un modèle de régression.
Une variable dichotomique prend deux valeurs. Elle est une variable codée Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝟎/𝟏} , où Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝟏} signale la présence d'un attribut et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝟎} son absence. Par exemple, la variable Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑑𝑒𝑚𝑜𝑐𝑟𝑎𝑡𝑖𝑒} prend une valeur de 1 lorsque le pays démocratique et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} lorsque le pays est non démocratiques. Par exemple, la variable Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑓𝑒𝑚𝑚𝑒} est codée par Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} femme et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} code la variable Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑛𝑜𝑛 𝑓𝑒𝑚𝑚𝑒} (les hommes).
Une variable dichotomique possède une propriété qui est utilise et qui nous permet de l’utiliser dans un modèle de régression. La moyenne de la variable correspond à la proportion des observations qui sont codées Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝟏} .
Par exemple, la moyenne de la variable démocratie (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.35} ) correspond à la proportion de pays démocratique (c’est-à-dire la proportion des observations codées Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} ). On peut donc traiter une variable dichotomique comme une variable continue et l’utiliser dans une régression linéaire.
Par exemple, on peut intégrer la variable 𝑑𝑒𝑚𝑜𝑐𝑟𝑎𝑡𝑖𝑒 dans l’équation suivante :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {𝑦} = 𝑏_0 + 𝑏_1𝑑𝑒𝑚𝑜𝑐𝑟𝑎𝑡𝑖𝑒}
Pour les pays non démocratiques (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑑𝑒𝑚𝑜𝑐𝑟𝑎𝑡𝑖𝑒 = 0} ) :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {𝑦} = 𝑏_0 + 𝑏_1𝑑(0) = 𝑏_0}
Pour les pays démocratiques (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑑𝑒𝑚𝑜𝑐𝑟𝑎𝑡𝑖𝑒 = 1} ) :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {𝑦} = 𝑏_0 + 𝑏_1𝑑(1) = 𝑏_0 + 𝑏_1}
Dans une équation de régression, le coefficient Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝒃} d’une variable dichotomique indique l’effet de la modalité Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝟏} par rapport à la modalité.
Dans notre exemple, le coefficient Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑏_1} indique l’effet d’être une démocratie sur la VD par rapport au groupe de référence, c’est-à-dire par rapport à l’effet d’être un pays non démocratique. Le coefficient Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle b_1} représente la différence de moyenne entre les pays démocratiques et les pays non démocratiques
Si notre VD est le niveau de répression, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle b_1} représente la différence de moyenne de répression entre les pays démocratiques et les pays non démocratiques. Si le coefficient Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle b_1} est statistiquement significatif, on en conclut que les pays démocratiques se différencient des pays non démocratiques quant à leur niveau de répression. Le coefficient Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑏_0} correspond à la, c’est-à-dire quand 𝑑𝑒𝑚𝑜𝑐𝑟𝑎𝑡𝑖𝑒 est égal à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} . Elle représente la moyenne de répression des pays non démocratiques.
Selon Braumoeller et Sartori dans Introduction: The Promise and Perils of Statistics in International Relations, publié en 2004, les problèmes suivants peuvent se poser :
- erreurs de spécification : les tests statistiques, par exemple si on procède à une régression, doivent se rapporter au mécanisme causal de la théorie qu’il prétend évaluer. Ne pas le faire correspond à une erreur de spécification. On distingue trois erreurs de spécification, la première est quand le chercher produit une analyse statistique sans ancrage théorique [1], lorsque la théorie est impossible à tester car trop imprécise ou futile [2], lorsque les chercheurs survient lorsque les chercheurs imposent un modèle statistique sur une théorie au lieu de construire un modèle pour tester une théorie [3]. On doit adapter un modèle à la théorie que l’on veut tester et on est toujours tributaire des variables que l’on a à disposition.
Une droite de régression peut être générée par ces quatre nuages de point différents mais avec des coefficients qui sont strictement identique. Cela constitue une erreur de spécification. La recommandation est de toujours regarder les nuages de point et précisément les données. Dans ce cas, c’est un modèle statistique imposé sur des données qui peut présenter une bonne qualité d’ajustement alors qu’il ne rend pas bien compte de la forme de la relation. Seul le premier nuage de point (en haut à gauche) est adéquat.
- erreurs d’inférence : si on fait une inférence causale sur quelque chose de peu important. Du point de vue substantiel, il ne semble pas y avoir de relation claire entre la variable dépendante et la variable indépendante. La significativité statistique est un élément mais il faut toujours regarder l’intensité ou la force de la relation permettant de déterminer si la relation est importante ou pas. Le lien entre intensité d’un effet donc fore de la relation, et la significativité substantielle dépend de la relation analysée. Cela dépend de ce qu’on attend théoriquement et du contexte. Par exemple, concernant les types de traitement d’une maladie mortelle, si les chances de survie augmentent même très faiblement mais de manière significative statistiquement, cela peut constituer quelque chose d’important.
Dans cet exemple, l’effet signification est extrêmement faible. On a procédé à une régression sur 50000 individus. La significativité statistique dépend de l’effectif. Si l’échantillon et grand, la plus infime variation observée va être significative faisant que les tests de significativité statistiques sont de peu d’utilité parce qu’il faut regarder l’intensité de la relation pour pouvoir apprécier et poser un diagnostique.
Le diagramme de dispersion ne montre aucune relation. La pente de la droite est quasiment plate. Il est plus facile de publier un article lorsqu’on valide une hypothèse alors qu’il est plus difficile de publier un article qui démontre l’absence d’une relation. On observe dans la littérature un tendance à tester beaucoup d’hypothèses.
Dans les années 1980 et 1990 les premières recherches systématiques se servent d’outils statistiques tels que les corrélations et la régression, comme par exemple le travaux de Park qui publie en 1987 Correlates of Human Rights: Global Tendencies, Mitchell et McCormick publient en 1988 Economic and political explanations of human rights violations, Henderson en 1991 publie Conditions affecting the use of political repression et Poe et Tate publient en 1994 Repression of human rights to personal integrity in the 1980s: a global analysis, pour évaluer des hypothèses concernant le respect des droits de l’homme.
Les travaux s’appuyant sur des régressions tentent de tenir compte du caractère « quasi-expérimental » des analyses en contrôlant pour d’autres variables. Le travail de Park se contente de calculer des coefficients de corrélation (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑟} ) et résume ces informations graphiquement.
Ce schéma présente des corrélations simples entre toutes les variables. Park s’appuie sur des coefficients de corrélation et regarde si les variables sont corrélées entre elles positivement ou négativement avec la variable que l’on cherche à expliquer. Par exemple, si on connaît les dépenses d’éducation d’un pays, on arrive assez bien à prédire le niveau de droits politiques parce que la corrélation est forte.
Par exemple, dans les pays où la population musulmane est importante, les droits politiques et économiques semblent être en moyenne plus faible car il y a des relations négatives.
La force de ces relations ne peut être utilisée pour faire une inférence causale. On ne peut pas argumenter qu’en augmentant les dépenses de l’État social, il y a un effet un effet causale sur le droits économiques. Pour faire ceci, on devrait s’assurer que les postulats ou que les conditions d’applications sont respectés et remplis. Ici, ce n’est pas le cas parce qu’il n’y a aucun contrôle par les autres variables. Sur la base de ces coefficients de corrélation, on ne peut uniquement décrire que comment ces variables sont reliées entre elles.
Avant de s’engager sur des analyses de régressions linéaires, dans Conditions affecting the use of political repression publié en 1991, Henderson présente d’abord des statistiques descriptives pour les variables utilisées dans ses analyses.
Henderson cherche à expliquer comment le niveau de démocratie affecte la répression. L’hypothèse principale qu’il veut évaluer est que le niveau de démocratie va influencer le niveau de répression. Il part de l’idée que ce n’est pas seulement le niveau de démocratie qui va assurer le non respect des droits de l’homme mais également l’inégalité économique, la croissance économique, le niveau de développement économique et les besoins socio-économiques d’un pays.
Il y utilise quatre variables de contrôle et trouve que lorsque les pays deviennent plus démocratiques, le niveau de répression diminue. Comme il contrôle par un certain nombre de facteurs susceptibles d’influencer le niveau de répression, il pourrait procéder à une inférence causale.
Sur la base de l’échantillon retenu, les coefficients estimés montre que lorsque le niveau de démocratie augmente, le niveau de répression diminue. La variable Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑑𝑒𝑚𝑜𝑐𝑟𝑎𝑡𝑖𝑒} à un effet négatif, plus le pays est démocratique et plus le niveau de répression dynamique, il y a un effet qui est significatif. Si on regarde l’inégalité économique, plus la valeur est positive et plus l’inégalité et forte. Il y a trois variables de contrôle est l’une des trois n’est pas significative qui est la dernière. Il relance une analyse est le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑅^2} évolue de manière marginale. Ce modèle explique pus de la moitié de la variation de la répression.
Poe et Tate pousse plus loin les variables démocratiques dans l’article Repression of human rights to personal integrity in the 1980s: a global analysis publié en 1994. Cet article s’intéresse à l’impact du niveau de démocratie sur l’intégrité individuelle des individus. Ce qui nous intéresse est la variable 𝑑𝑒𝑚𝑜𝑐𝑟𝑎𝑡𝑖𝑒. Dans la littérature, il existe plusieurs possibilités pour calculer le niveau de démocratie. Les petites étoiles renvoient au niveau de significativité qui est la probabilité d’erreur indiquant les variables qui ont un effet signification. Le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑅^2} indique la qualité du modèle. C’est un exemple de linéarité multiple dans le contexte des droits de l’homme.
Comme le travail de Rai publié en 1980 intitulé Foreign Aid and Voting in the UN General Assembly, 1967-1976, celui de Kegley et Hook intitulé U.S. Foreign Aid and U.N. Voting: Did Reagan's Linkage Strategy Buy Deference or Defiance? publié en 1991 s’intéresse à la question qu’est-ce qui explique les décisions d’allocations d’aide au développement (des États-Unis).
Kegley et Hook veulent évaluer la politique proposée par le président Ronald Reagan de lier l’aide bilatérale au soutien des positions des États-Unis lors de votes importants au sein de l’assemblée générale de l’ONU. Étudiant les allocations d’aide bilatérale des États-Unis dans la deuxième moitié des années 1980, Kegley et Hook évaluent à la fois le lien entre les votes à l’assemblée générale et l’aide bilatérale, et le lien entre l’aide et ces votes.
Ce schéma est un ensemble de régressions multiples. Les coefficients sont standardisés. Par exemple les coefficients qui lient l’aide de 185 à 186 sont très élevés. Idem pour les coefficients qui lient le vote 1984 au vote 1985. L’explication est que le montant reçu l’année précédente explique le vote. Si un pays a fortement voté avec les États-Unis en 1984, il vote avec les États-Unis en 1985. Les relations restent stables sur la période considéré. Les coefficients qui montre le lien entre l’aide au développement et le vote e les liens entre les votes et l’aide au développement sont marginaux. C’est ne changeant un comportement de vote qu’on peut amener les États-Unis à amener plus d’aide aux États-Unis.
Les auteurs essaient d’expliquer les changements en fonction de l’aide obtenue par les pays. La variable dépendante est la différence d’accords de vote entre 1984 et 1985 et la variable indépendante est l’aide reçue par les pays. Les coefficients présentés sont non standardisés. On distingue quatre période permettant d’élaborer quatre modèle de régression. Seul un coefficient est significatif. Ils trouvent uniquement des changements pour les relations de 1987 à 1988 qui est un changement assez lié avec l’aide que les pays ont reçus.
La variable dépendante est le changement de vote des États-Unis et la variable indépendante est le PNB par reçu par les États-Unis.
L’inférence causale à l’aide de régressions linéaires (et d’ailleurs d’autres outils du même type) nous force à accepter une série de postulats. Dans un modèle de régression linéaire, on peut ajuster une courbe.
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑦 = 𝑏_0 + 𝑏_1𝑥 + 𝑏_2𝑥^2 + 𝑛}
Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑏_0>/math> , <math>𝑏_1} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑏_2} sont les paramètres, s’ils s’additionnent, il y a une linéarité et il n’y a pas de problèmes.
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑦 = 𝑏_0 + 𝑥^{b1} + 𝑏_2x + 𝑛}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑦 = 𝑏_0 + 𝑥^{b1x} + 𝑏_2x + 𝑛}
Ces deux équations ne pas linéaires en paramètre parce que le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑏} ne s’additionne pas avec les autres.
Dans le domaine international, le postulat d’un échantillon aléatoire n’est pas toujours rempli, donc nous devons nous assurer qu’en tenant compte de nos variables explicatives, nos observations sont indépendantes les unes des autres.
Braumoeller et Sartori dans Introduction: The Promise and Perils of Statistics in International Relations publié en 2004 nous avertissent également par rapport aux problèmes de la spécification correcte de notre modèle et de l’inférence.
Tableaux bivariés et multivariés[modifier | modifier le wikicode]
Les niveaux de mesure de la variable dépendante et de la variable indépendante déterminent le choix de l’outil utilisé pour analyser cette relation. Nous avons vu jusqu’à présent le cas de figure où les deux variables sont d’intervalles et où l’outil à utiliser pour analyser la relation est la régression.
Quel outil utiliser lorsque l’une ou les deux variables de la relation bivariée sont catégorielles (nominales ou ordinales) ?
Tableaux croisés[modifier | modifier le wikicode]
Un tableau croisé (ou tableau de contingence) est un croisement entre deux variables catégorielles (nominales ou ordinales) dans un tableau. L’analyse d’un tableau croisé permet de déterminer si deux variables sont associées. Les tableaux croisés permettent de tester des hypothèses chaque cellule contient un nombre d’observations qui est une fréquence correspondant à un nombre de modalités présentées en ligne et en colonne.
Dans cet exemple, on a des variables dichotomiques et sont représentées des fréquences. On cherche à tester l’hypothèse suivante
On va chercher à tester l’hypothèse que les femmes se sentent davantage que les hommes en insécurité pendant la nuit
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Femme\ → Sentiment\ d’insécurité}
Le genre est la VI et le sentiment d’insécurité est la VD. La relation est asymétrique car on suppose que le genre influence le sentiment d’insécurité, qu’il y a une relation de cause à effet.
Pour déterminer s’il existe une relation entre les deux variables et tester notre hypothèse, on va comparer le pourcentage d’hommes en insécurité au pourcentage de femmes en insécurité :
- si le pourcentage d’hommes en insécurité n’est pas diffèrent du pourcentage de femmes en insécurité, il n’y a pas de relation entre les deux variables : elles sont statistiquement indépendantes ;
- en revanche, plus ces pourcentages varient, plus la relation entre les deux variables est forte : elles sont statistiquement dépendantes.
La règle est que lorsqu’on teste une hypothèse avec un tableau croisé, les pourcentages doivent être calculés dans chaque catégorie de la variable indépendante :
- si la variable indépendante est mise en colonne dans le tableau croisé, cette règle implique de calculer chacun des pourcentages en utilisant comme base l’effectif total de la colonne.
- si la variable indépendante est mise en ligne dans le tableau croisé, cette règle implique de calculer chacun des pourcentages en utilisant comme base l’effectif total de la ligne.
Le choix de la VI dépend de l’hypothèse formulée.
Pourquoi faut-il comparer les pourcentages à l’intérieur des catégories de la VI ? Pour comparer si les catégories de la VI se différencient par rapport à la VD. Cela permet de neutraliser le poids numérique (effectifs marginaux) différent des catégories de la VI que l’on veut comparer.
Ici, les catégories ont été calculées à l’intérieur de la variable indépendante.
Ce tableau permet de poser un diagnostique rapide sur l’hypothèse que l’on veut tester. On calcule les pourcentage en colonne et on analyse ligne par ligne. Sur la première ligne, on voit que les hommes sont plus en sécurité que les femmes. On prend ensuite la deuxième ligne et on regarde s’il y a un écart entre les hommes et les femmes. C’est comme cela qu’on test une hypothèse entre deux variables catégorielles.
Pour déterminer dans le tableau croisé si la VI exerce une influence sur la VD, on peut regarder les variations de pourcentage entre les catégories de la VI. En comparant les pourcentages entre les catégories de la VI, de grandes différences qui indiquent une forte relation entre les variables et aucunes différences ne signifie pas de relation. Dans notre exemple, on compare le pourcentage de femmes en insécurité et le pourcentage d’hommes en insécurité. Le genre semble influencer le sentiment d’insécurité.
La différence de pourcentage entre hommes et femmes s’élève à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 22.9 – 6.4 = 16.5} points de pourcentage. Sur cette base, il semble que le genre influence le sentiment d’insécurité. On regarde les variations. Parfois il faut utiliser d’autres mesures parce que parfois les mesures ne sont pas toujours congruentes entre elles.
Il existe également d’autres mesures comme :
- le rapport de pourcentage : les femmes se sentent Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {22.9}{6.4} = 3.6} fois plus en insécurité pendant la nuit que les hommes ;
- l’odds ratio : les femmes ont 4.4 fois plus de chances que les hommes de se sentir en insécurité plutôt que de se sentir en sécurité. L’Odds ratio = Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle (22.9/(100-22.9)/(6.4/(100-6.4)) = 4.3} (sans les arrondis, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 4.4} ).
Il est possible de calculer les pourcentage attendus sous l’hypothèse nulle, c’est-à-dire qu’il n’y a pas de différence de pourcentage entre les catégories. C’est un exemple où il n’y a pas de relations entre les deux variables.
Le test du chi-carré est un test de signification statistique qui permet de déterminer si la relation découverte à partir de données d’échantillon est due au hasard de l’échantillonnage.
C’est un test d’ajustement qui examine si les fréquences observées (dans le tableau bivarié) et les fréquences attendues sous l’hypothèse nulle (fréquences attendues s’il n’y a pas de relation entre les deux variables) sont bien ajustées :
- si les fréquences observées sont très différentes des fréquences attendues sous Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} , on rejette Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} et on conclut qu’il existe une relation entre les deux variables au sein de la population ;
- si les fréquences observées sont similaires aux fréquences attendues sous Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} , on ne peut pas rejeter Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} et on conclut qu’il n’y a pas de relation entre les deux variables.
On va chercher à rejeter Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} et à accepter Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_1} :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} : il n’y a pas de relation entre les deux variables (les deux variables sont statistiquement indépendantes) ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_1} : les femmes se sentent davantage que les hommes en insécurité pendant la nuit (le genre influence le sentiment d’insécurité).
Le test requiert de travailler sur un échantillon aléatoire. Le test du chi-carré est symétrique. Ce test permet de vérifier si les modalités sont dépendantes ou pas.
- Fréquence attendue sous Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} pour les hommes en sécurité: Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 797 \times \frac {1488}{1760} = 673.8}
- Fréquence attendue sous Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} pour les femmes en sécurité : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 963 \times \frac {1488}{1760} = 814.2}
- Fréquence attendue sous Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} pour les hommes en insécurité : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 797 \times \frac {272}{1760} = 123.2}
- Fréquence attendue sous Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} pour les femmes en insécurité : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 963 \times \frac {272}{1760} = 148.8}
La formule pour calculer le chi-carré est la suivante :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle χ^2 = Σ \frac {(f_o - f_a)^2}{f_a}}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle χ^2} = chi-carré
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle f_o} = fréquence observée de chaque cellule
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle f_a} = fréquence attendues sous Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} de chaque cellule
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle f_o- f_a} représente l’écart à l’indépendance/résidu 𝑜𝑎
Plus la valeur du Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle χ^2} est grande, plus on a des indices contre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} : indépendance.
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle χ^2 = Σ \frac {(f_o - f_a)^2}{f_a} =\frac {72.2^2}{673.8} + \frac {-72.2^2}{814.2} + \frac {-72.2^2}{123.2} + \frac {72.2^2}{148.8} = 91.48}
Les 6 éléments du test d’indépendance du chi-carré :
- 1) Postulats : 2 variables catégorielles, échantillon aléatoire, 80% des cellules Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle f_a ≥ 5} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle f_a ≥ 1} dans toutes les cellules Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle a}
2Hypothèses :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} : Indépendance statistique des variables ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_1} : Dépendance statistique des variables.
- 3) Test statistique : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle χ^2 = Σ (f_o-f_a )^2/f_a} , où Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle f_a} =(total ligne)(total colonne)/((total échantillon) )
- 4) Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle P - value} : probabilité d’erreur du test de chi-carré
- 5) Fixer le seuil de signification : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.05} (on peut choisir un autre seuil)
- 6) Conclusion
- Si la Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p - value ≤ 0.05} , rejet de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} → relation statistiquement significative ;
- Si la Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p - value > 0.05} , on ne peut pas rejeter Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} → relation non significative.
Si, sur la base des résultats, on conclut que la relation entre les deux variables existe au sein de la population (on rejette l'hypothèse nulle) alors que ce n'est pas le cas (en réalité, il n’y a pas de relation au sein de la population), on commet une erreur statistique car la relation observée au sein de l’échantillon est induite par les fluctuations aléatoires. Elle est appelée erreur statistique de première espèce ou erreur alpha (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝛼} ).
Le Pearson Chi-Square est le test du chi-carré. La probabilité d’erreur (Asymp. Sig. (2-sided)) du test du chi-carré est inferieure au seuil qu’on a fixé par convention à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.05} . On rejette Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} et on conclut que la relation entre le genre et le sentiment d’insécurité est statistiquement significative.
Le test du chi-carré est adapté pour de grands échantillons. Pour que les résultats du chi carré soient valides, il ne doit pas y avoir, dans le tableau croisé plus de 20% des cellules contenant des fréquences attendues (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle f_a} ) sous Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} inférieur à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 5} ou bien une cellule avec une fréquence attendue (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle f_a} ) sous Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} inferieure à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} .
Le test exact de Fisher est adapté pour de petits échantillons. Le test exact de Fisher teste s’interprète exactement de la même façon que le test du chi-carré.
Pour décrire la structure d’association entre deux variables, il faut examiner quelles sont les cellules qui s’écartent de l’indépendance. La différence entre la fréquence observée dans une cellule et la fréquence attendue sous Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} de cette cellule (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle f_o - f_a} ) représente l’écart à l’indépendance/résidu :
- un résidu positif indique que Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle f_o > f_a} ;
- un résidu négatif indique que Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle f_o < f_a} .
Pour déterminer si un résidu est assez grand pour indiquer un écart à l’indépendance qui n’est pas dû au hasard de l’échantillonnage, on utilise le résidu standardisé ajusté. Quand Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} est vraie, il y a environ 5% de chances qu’un résidu standardisé ajusté dépasse Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 2} en valeur absolue. Les valeurs inférieures à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -2} ou supérieures à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 2} sont des indices d’un vrai effet dans la cellule. Les valeurs inférieures à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -3} ou supérieures à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 3} sont des indices convaincants d’un vrai effet dans la cellule.
Les résidus standardisés ajustés supérieurs à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 2} en valeur absolue indique un écart significatif de la cellules à la situation d’indépendance au seuil de 5%.
Le tableau montre des grands résidus ajustés positif pour les hommes qui se sentent en sécurité (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 9.6} ) et les femmes qui se sentent en insécurité (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -9.6} ). Cela signifie qu’il y a plus d’hommes qui se sentent en sécurité et plus de femmes qui se sentent en insécurité que ce que prédit l’hypothèse d’indépendance. À l’inverse, il y a moins d’hommes en insécurité (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -9.6} ) et de femmes en sécurité (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -9.6} ) qu’on pourrait s’attendre si le sentiment d’insécurité était indépendant du genre.
Le découpage des variables en modalités (catégories) peut influencer fortement le résultat du test du chi-carré. Un regroupement de modalités peut faire apparaître ou masquer des écarts à l’indépendance. Le test du chi-carré est très sensible à l’effectif total du tableau. Le résultat du test du chi-carré n’informe pas sur la force du lien entre les deux variables mais permet simplement de savoir si on peut inférer les résultats à la population. Le test du chi-carré d’indique pas si toutes les cellules du tableau s’écartent de l’indépendance ou si c’est seulement une ou deux cellules qui s’écartent de l’indépendance.
Les coefficients d'association permettent de déterminer la force de la relation entre les deux variables (résumés statistiques, information concentrée en un chiffre). De manière générale, ces résumés statistiques sont standardisés. Ils varient entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -1} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} ou entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} . Plus le chiffre se rapproche de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} (ou Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -1} ), plus la relation entre les deux variables est forte. Plus le chiffre est proche de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} , plus la relation est faible
Les coefficients d’association sont directement liés au niveau de mesure des variables (nominal, ordinal, intervalles).
Si les deux variables sont catégorielles dont l’une au moins est nominale, on utilise :
- Lambda (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle λ} )
- V de Cramer
Si les deux variables sont ordinales, on utilise :
- Gamma (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle γ} )
Si la variable dépendante est d’intervalles et la variable indépendante catégorielle (nominale ou ordinale), on utilise :
- Eta (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle η} )
Cette liste des coefficients d’association n’est pas exhaustive.
Le V de Cramer est un coefficient d’association approprié si les deux variables sont catégorielles et que l’une ou les deux sont nominales. Il varie de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} : plus sa valeur se rapproche de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} et plus la relation entre les variables est forte.
Le gamma (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle γ} ) est un coefficient d’association approprié si les deux variables sont ordinales. Une relation entre deux variables ordinales peut être positive ou négative (direction, sens de la relation indiquée par le signe). Il varie de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle –1} à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} : une valeur proche de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} indique une absence de relation entre les deux variables ; une valeur proche de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} ou Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle –1} signale une relation très forte positive ou négative.
L’eta (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle η} ) est un coefficient d’association approprié pour une variable dépendante d’intervalles et une variable indépendante catégorielle (nominale ou ordinale). Il varie de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} : une valeur proche de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} indique une forte relation.
On cherche à tester l’hypothèse suivante : en Grande-Bretagne, la peur d’un attentat terroriste dans le pays augmente avec l’âge :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle âge → peur\ d’un\ attentat\ terroriste}
L’âge est la VI et la peur d’un attentat terroriste est la VD. La relation est asymétrique car on suppose que l’âge influence la peur d’un attentat terroriste. La mesure de la peur d’un attentat terroriste se fera avec la question suivante : pour vous, un attentat terroriste en Grande-Bretagne au cours de ces douze prochains mois est très probable, plutôt probable, peu probable ou pas probable du tout ? La peur d’un attentat terroriste est une variable nominale en 2 catégories (probable, non probable). L’âge est une variable ordinale en 4 catégories.
Pour déterminer s’il existe une relation entre les deux variables et tester notre hypothèse, on va comparer le pourcentage des différents groupes d’âge qui considèrent comme probable un attentat terroriste dans le pays.
On constate qu’il y a 7 variables indéterminées. Pour déterminer s’il u a une relation entre les deux variables, on interprète ligne après ligne. Les individus qui considéré comme non problème les attaques terroristes sont de 38% pour les jeunes diminuant avec l’avancée en âge. Au contraire, plus l’âge est élevé, plus la peur d’une attaque terroriste est élevée.
La relation est significative car la probabilité d’erreur (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.000} ) est inferieur à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.05} (seuil fixé par convention). On écrit Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p < 0.05} .
Dans ce cas, on a très peu de chance de se tromper en affirmant que la relation observée dans l’échantillon se retrouve au sein de la population.
L’association entre l’âge et la peur d’un attentat terroriste est plutôt modérée.
Les résidus standardisés ajustés supérieurs à 2 en valeur absolue indique un écart significatif de la cellules à la situation d’indépendance au seuil de 5% La relation entre l’âge et la peur d’un attentat terroriste est significative et modérément forte. Notre hypothèse est vérifiée.
On cherche à tester l’hypothèse suivante : plus les personnes disposent d’un niveau scolaire élevé, moins elles ont une attitude traditionnelle vis-à-vis des rôles sexuels.
L’éducation est la VI et attitude vis-à-vis des rôles sexuels est la VD. L’attitude vis-à-vis des rôles sexuels sera mesurée avec le degré d’accord avec la proposition « lorsque les emplois sont rares, la priorité devrait être donnée aux hommes plutôt qu'aux femmes pour avoir un emploi ». L’éducation a 5 catégories (de 1 le plus bas niveau à 5 le plus élevé). L’attitude vis-à-vis des rôles sexuels a 5 catégories (de 1 fortement d’accord avec la proposition qui correspond à une attitude traditionnelle à 5 fortement en désaccord qui correspond à une attitude égalitaire).
Pour déterminer s’il existe une relation entre les deux variables et tester notre hypothèse, on va comparer le pourcentage de personnes d’accord avec la proposition pour chacun des niveaux de formation.
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p < 0.05} → la relation est significative.
La valeur du coefficient Gamma indique que la relation est relativement forte et positive ce qui signifie que plus une variable augmente, plus l’autre augmente.
La relation est statistiquement significative et relativement forte. Notre hypothèse est vérifiée : l’attitude traditionnelle vis-à-vis des rôles sexuels diminue avec le niveau scolaire.
Ce tableau résume la relation entre le niveau de formation et l’intérêt pour la politique. L’hypothèse est que plus on est éduqué et plus on est intéressé par la politique avec un gamma négatif. Les données vont dans le sens de l’hypothèse mais on obtient un gamma négatif.
La probabilité d’erreur (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.000} ) < Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.05} (seuil fixé) → la relation est significative.
La valeur du coefficient gamma indique que la relation est relativement forte et négative → plus une variable augmente, plus l’autre diminue.
Ce tableau résume le rapport entre la classe d’âge et les partis voté. La variable parti voté est une variable nominale et on ne peut pas utiliser le gamma.
Il est important de connaître le codage des variables.
La relation est significative car la probabilité d’erreur (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.018} ) est inférieur à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0,05} (seuil fixé par convention). On écrit Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p < 0.05} . Dans ce cas, on a 1,8% de chance de se tromper en affirmant que la relation observée dans l’échantillon se retrouve au sein de la population.
L’association entre l’âge et le choix partisan est plutôt faible.
Tableaux de moyennes[modifier | modifier le wikicode]
Les tableaux de moyennes sont appropriés pour analyser une relation entre une VI qualitative et une VD quantitative (d’intervalles).
On cherche à tester l’hypothèse suivante : plus l’âge augmente, plus le niveau de conservatisme augmente. La relation est asymétrique car on suppose que l’âge influence le niveau de conservatisme. Pour déterminer s’il existe une relation entre les deux variables et tester notre hypothèse, on va comparer la moyenne de conservatisme des différentes classes d’âge.
Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_1} : Plus l’âge augmente, plus le niveau de conservatisme augmente. L’hypothèse est confirmée par l’augmentation du niveau moyen de conservatisme avec l’âge. Il faut regarder l’écart au sein des groupes. Les écart-types sont importants mais les groupes sont distincts tandis que l’évolution des moyennes va dans le sens de l’hypothèse. Il faut être attentif à l’effectif de chaque catégorie.
- Variance intergroupes
On va regarder les relations entre les différents groupes (catégories) de la VI. Les groupes sont clairement distincts, différents, pas superposés ? Il faut regarder les différences de moyennes entre les groupes.
- Variance intra-groupes
On va regarder les relations entre les individus/cas à l’intérieur de chacun des groupes de la VI. Les groupes sont homogènes ou plutôt hétérogènes? Il faut regarder les écarts-types de chaque groupe.
Pour confirmer la relation, on cherche une faible variance intra-groupes et forte variance inter-groupes (des groupes homogènes et bien distincts).
L’analyse de la variance (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle ANOVA} ) produit le test F. Le test F compare la variance entre les catégories (variance intergroupe) et la variance à l’intérieur des groupes (variance intragroupe). La probabilité d’erreur du test F (sous Sig. = 0.000) est inférieure seuil de signification fixé par convention à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.05} . On peut rejeter Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} .
La relation entre la VI catégorielle (âge) et la VD quantitative (conservatisme) est statistiquement significative. Les classes d’âge affichent des moyennes de conservatisme différentes.
Le coefficient d’association eta (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle η} ) indique la force de la relation. Il s’interprète comme les autres coefficients d'association. Il varie de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} : une valeur proche de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} indique une forte relation.
Le coefficient eta2 (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle η^2} ) indique la puissance explicative du modèle, c’est-à-dire le pourcentage de variation de la VD expliqué par la VI. L’interprétation est similaire au Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle R^2} d'une régression linéaire.
Dans Statistical power analysis for the behavioral sciences publié en 1988, Cohen distingue plusieurs coefficients :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle η^2 = 0.01} faible ; Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle η^2 = 0.06} modéré ; Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle η^2 = 0.14} fort
La relation entre l’âge et le niveau de conservatisme est statistiquement significative (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p < 0.05} ) et forte. L’âge explique 15.8% du niveau de conservatisme des individus. L’inspection du tableau de moyennes confirme que la relation va dans le sens de notre hypothèse. Plus l’âge augmente, plus le niveau de conservatisme augmente.
Tableaux croisés multivariés[modifier | modifier le wikicode]
Deux questions sont intéressantes :
- la relation est-elle véritablement causale ? Ou n’est-elle pas plutôt une relation fallacieuse engendrée par une quelconque tierce variable ?
- quelles sont les variables intermédiaires qui relient la VI et la VD ?
Une des trois conditions pour conclure à une relation causale est d’éliminer les explications alternatives. La relation entre les variables Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle X_1} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Y} ne doit pas être due à une troisième variable Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle X_2} . On ne peut jamais prouver qu’une variable est la cause d’une autre. On peut réfuter une hypothèse causale en montrant que la relation entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle X_1} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Y} est en réalité due à une troisième variables ou à un ensemble de variables. La recherche d’explication alternative se fait en introduisant une ou plusieurs variables dites de contrôle.
Les variables que l’on introduit pour tester une relation de causalité sont appelées des variables de contrôle. Une relation entre deux variables est susceptible d’être déterminée par d’autres variables qu’on appelle variables de contrôle. L’introduction d’une variable de contrôle permet de vérifier l’existence une relation entre deux variables. La variable de contrôle fonctionne comme une sorte de seconde variable indépendante.
On examine la relation entre la participation politique, mesurée par le vote lors des dernières élections fédérales et l’âge. L’hypothèse est que l’âge favorise la participation politique (plus on est âgé, plus on participe). Pour pouvoir parler d’une relation causale, il faut tester des explications alternatives. On va introduire l’éducation comme variable de contrôle. Les variables sont : participation (oui/non), âge (<34/35-64/65+), éducation (obligatoire/secondaire/tertiaire)
Au niveau bivarié, la relation est significative et modérée. L’hypothèse est confirmée donc, les deux variables sont associées. On va introduire l’éducation comme variable de contrôle. On produit autant de sous-tableaux (tableaux partiels) qu’il y a de catégories de la variable de contrôle. On analyse la relation bivariée initiale entre la participation politique et l’âge pour chaque niveau de formation.
On regarde pour chacun des niveaux de formation si la relation initiale se renforce ou persiste.
Pour le premier tableau, la relation s’est renforcée. Pour le deuxième tableau, la relation va toujours dans la même direction. Pour le troisième tableau, il semble qu’il y ait une variation mais qui est beaucoup plus faible. À ce stade on ne sait pas si la relation est significative. Pour le niveau tertiaire, la relation n’est plus significative. On ne peut pas conclure à un effet de l’âge sur la participation.
On regarde les coefficients d’association. Le V de Crammer est identifie pour les deux premiers tableaux. La variable de contrôle permet de nuancer et d’affiner la relation mise en évidence. L’effet existe mais en fait il n’existe pas pour ceux qui ont un niveau d’éducation élevé.
Tableaux de moyennes multivariés[modifier | modifier le wikicode]
La démarche avec les tableaux de moyennes est strictement identique à celle utilisée pour les tableaux croisés.
On cherche à tester l’hypothèse causale suivante : plus on est âgé, moins on trouve justifié l’avortement. On Introduit l’éducation comme variable de contrôle. On produit autant de sous-tableaux (tableaux partiels) qu’il y a de catégories de la variable de contrôle. On analyse la relation bivariée initiale entre l’avortement et l’âge pour chaque niveau de formation
Il y a trois variables :
- avortement : échelle de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} , jamais justifié, à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 10} , toujours justifié ;
- âge : 15-34, 35-49, 50-64, 65+ ;
- éducation : obligatoire/apprentissage/supérieur.
Au niveau bivarié, on constate que moins on est âgé moins on est élevé dans l’échelle. On observe un fossé important entre le 50-64 et 65+ où les écarts sont importants. Le test F est significatif et l’Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle eta^2} est de 5,9%.
Le test est significatif pour le niveau obligatoire et apprentissage mais n’est plus supérieur au niveau supérieur. L’eta pour le niveau obligatoire est 12%. Pour le niveau apprentissage cela est moins fort mais avec 4,6% de relation expliquée. Et pour le niveau supérieur l’eta est de 1,7% soit un niveau peu explicatif. Si on regarde la relation bivariée, on aurait conclu que l’âge influence l’attitude face à l’avortement, en réalité, cette effet s’exerce que pour ceux qui on un niveau de formation obligatoire ou de niveau apprentissage.
Ce tableau a trait à la mesure des inégalités des chances scolaires afin d’illustrer que la comparaison des pourcentages n’est parfois pas si facile qu’on pourrait le penser. On distingue les enfants d’ouvrier et les enfants de cadres.
La question est : en 50 ans, l’inégalité des chances selon l’origine sociale a-t-elle augmenté, diminué, ou bien est-elle restée constante ?
- Basé sur la différence de pourcentage, on a une augmentation des inégalités. L ‘écart s’est accru entre aujourd’hui et il y a 50 ans. Il est passé de 40 points à 45 points en faveur des enfants de cadre. Les inégalités ont augmenté.
- Sur la base d’un rapport de pourcentage, il y a 50 ans, les enfants de cadre sont Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {45}{5} = 9} fois plus nombreux (en pourcentage) à obtenir le baccalauréat que les enfants d’ouvriers. Aujourd’hui’ les enfants de cadre sont Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {90}{45} = 2} fois plu nombreux (en pourcentage) à obtenir le baccalauréat que les enfants d’ouvrier. La conclusion est que les inégalités d’obtention du bac ont diminué.
Il y a une contradiction dans les conclusions. Que peut-on conclure par rapport à la question de l’évolution de l’inégalité des chances ? Peut-on se satisfaire du constat de la contradiction quand on traite des mêmes données ? Est-ce qu’on n’attend pas de la statistique une conclusion univoque ? Et plus généralement, en matière de science, peut-on se satisfaire du constat de la contradiction ? Comment trancher entre ces deux mesures contradictoires ?
Il y a une contradiction. La statistique ne permet pas de répondre aux questions qu’elle soulève. Avec ces données qui sont assez simple, on doit trancher.
- Première mesure : différence de pourcentages
Il y a 50 ans, le pourcentage de non obtention du bac est de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 95 – 55 = 40} points plus élevés chez les enfants d’ouvriers que chez les enfants de cadres. Aujourd’hui, le pourcentage de non obtention du bac est de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 55 – 10 = 45} points plus élevés chez les enfants d’ouvriers que chez les enfants de cadres. La conclusion est que l’écart de non obtention du bac s’est accru entre aujourd’hui et il y a 50 ans. Il est passé de 40 points à 45 points. Les inégalités ont augmenté. La différence de pourcentage est une mesure cohérente.
- Deuxième mesure : rapports entre pourcentages
Il y a 50 ans, les enfants d’ouvriers sont Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {95}{55} = 1.7} fois plus nombreux (en pourcentage) à ne pas obtenir le bac que les enfants de cadres. Aujourd’hui, les enfants de cadres sont Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {55}{10} = 5.5} fois plus nombreux (en pourcentage) à obtenir le baccalauréat que les enfants d’ouvriers. En conclusion, les inégalités de non obtention du bac ont augmenté.
La mesure du rapport entre pourcentages inverse sa conclusion. L’inégalité des chances d’obtenir le bac diminue mais l’inégalité de ne pas obtenir le bac augmente. Les rapports entre pourcentages est une mesure incohérente. C’est un terme utilisé pour qualifier une mesure dont la conclusion s’inverse selon qu’on l’applique à des pourcentages ou à leurs complémentaires.
- Troisième mesure : les taux de variation par rapport au maximum de variation possible
Elle consiste à comparer la variation réelle des pourcentages à la longueur du chemin qui reste à parcourir pour atteindre le pourcentage maximum de 100%. C’est le taux de variation par rapport au maximum de variation possible. Cette mesure consiste à diviser la progression effectuée par le maximum de la progression possible.
Il y a 50 ans, les enfants de cadres ont amélioré leur pourcentage d’obtention du bac de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle (90 – 45) = 45} points (« chemin parcouru »), alors qu’ils pouvaient l’améliorer au maximum de (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 100 - 45} ) 55 points (« chemin qui, il y a 50 ans, restait à parcourir »). Ils l’ont donc amélioré de (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {45}{55} \times 100} ) 82% du maximum de variation possible. Les enfants d’ouvriers ont amélioré de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {45 – 5}{100 – 5} \times 100} = 42% du maximum de variation possible. Les enfants de cadres ont réduit plus vite que les enfants d’ouvriers la distance qui les séparait de l’idéal des 100% de réussite au bac. La conclusion est que les inégalités d’obtention du bac ont augmenté.
- Quatrième mesure : les « odds ratio »
Les odds ratio (les rapports de chances relatives) sont la mesure qui s’est imposée pour mesurer les inégalités. L’odds ratio est au centre de plusieurs méthodes statistiques utilisées pour la modélisation des données catégorielles (ex., la régression logistique). Cette mesure consiste à calculer et comparer des odds (chances relatives, autrement dit le rapport entre le taux de réussite et le taux d’échec).
En statistique, le terme odds – qui peut se traduire par cote ou chance relative – désigne le rapport d’une proportion, d’un effectif ou d’une probabilité à son complémentaire.
Par exemple :
- si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} est une proportion : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {p}{1 – p}} ;
- si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} est un pourcentage : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {p}{100 – p}} .
Odds – Enfants de cadre aujourd’hui :
- 90% obtiennent le bac ;
- 10% (100 – 90) ne l’obtiennent pas ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Odds_{cadre.auj} = \frac {90}{100 – 90} = \frac {90}{10} = 9} fois plus d’enfants de cadres qui obtiennent le bac que d’enfants de cadres qui n’obtiennent pas le bac.
C’est « l’odds », ou « chance relative », ici d’obtenir le bac plutôt que de ne pas l’obtenir. Pour les enfants de cadres, la chance relative d’obtenir le bac est de 9 contre 1.
Odds – Enfants d’ouvriers aujourd’hui :
- 45% obtiennent le bac ;
- 55% (100 – 45) ne l’obtiennent pas ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Odds_{ouvr.auj} = \frac {45}{55} = 0.82} fois plus d’enfants d’ouvriers qui obtiennent le bac que d’enfants de cadres qui n’obtiennent pas le bac.
Pour les enfants d’ouvriers, la chance relative d’obtenir le bac est de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.82} contre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} .
Odds ratio – aujourd’hui : Dans cet exemple, c’est le rapport entre les chances relatives (odds) des enfants de cadres d’avoir le bac et celles des enfants d’ouvriers
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Odds_{cadre.ouvr.auj} = \frac {Odds_{cadre.auj}}{Odds_{ouvr.auj}} = \frac {\frac {90}{100 - 90}}{\frac {45}{100 - 55}} = \frac {9}{0,82} = 11}
Autrement dit, les enfants de cadres ont 11 fois plus de chances que les enfants d’ouvriers d’obtenir le bac plutôt que de ne pas l’obtenir.
Odds ratio – il y a 50 ans :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Odds_{cadre.ouvr.50an} = \frac {Odds_{cadre.50ans}}{Odds_{ouvr.50ans}} = \frac{\frac{45}{100 - 45}}{\frac {5}{100-5}} =15,5}
Donc, il y a 50 ans, les enfants de cadres avaient 15,5 fois plus de chances que les enfants d’ouvriers d’obtenir le baccalauréat que de ne pas l’obtenir.
En conclusion, mesurées par les odds ratio, les inégalités d’obtention du bac ont diminué en 50 ans.
L’odds ratio mesure l’association statistique entre deux variables dichotomiques, dans notre cas le niveau de formation (obtention du bac/non obtention du bac) et l’origine sociale (cadres/ouvriers). Il prend ses valeurs entre 0 et +∞. Il vaut 1 en cas d’indépendance statistique. C’est-à-dire si les chances d’obtenir le bac plutôt que de ne pas l’obtenir étaient exactement semblables pour les enfants de cadres et les enfants d’ouvriers.
L’odds ratio est une mesure d’association très asymétrique :
- compris entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} si l’association est « dans une direction » ;
- varie entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle +∞} si elle est « dans l’autre direction ».
Par exemple, un odds ratio de 0.2 traduit la même intensité d’association statistique qu’un odds ratio de 5.
Pour rétablir la symétrie de la mesure, on utilise le logarithme naturel de l’odds ratio (Log odds ratio) :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Ln(1) = 0} indique l’indépendance statistique ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Ln(0.2) = -1.61} ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Ln(5) = 1.61} .
Les log odds ratio sont utilisés dans la régression logistique.
D’après un exemple tiré de Rouanet, Henry, "Barouf à Bombach", Echo des Messaches oublié en novembre 1978. Au cours d'un débat télévisé sur "la femme et les études scientifiques", on aborde la question de la réussite au bac C au cours de l'année précédente. Un premier participant fournit des statistiques pour la ville de Bombach sur la réussite au bac selon le sexe.
Il en déduit les pourcentages de réussite au bac selon le sexe. La conclusion est que les filles réussissent mieux que les garçons ; la différence est de 20 points de pourcentage en faveur des filles.
Un deuxième participant fait état d’un dossier plus détaillé qui fournit les résultats par lycée (dans la ville de Bombach, il y a deux lycées : Anastase et Bénédicte)
En ajoutant case à case ces deux tableaux, on retrouve le tableau pour la ville de Bombach.
Il en déduit les pourcentages de réussite au bac selon le sexe contrôlé par le lycée
La conclusion est qu’à l’intérieur de chacun des deux lycées, les garçons réussissent mieux que les filles la différence des pourcentages de réussite est la même dans les deux lycées : 20 points en faveur des garçons valeur opposée à la valeur globale calculée sur la ville de Bombach.
Est-ce que les conclusions des deux participants au débat sont correctes ? Comment expliquer cette inversion de la relation ? Les deux conclusions sont correctes. Une relation statistique a été contrôlée par l’établissement. Quand on contrôle par une variable, une relation statistique peut s’inverser. L’effet de structure est un phénomène structurel qui est la surreprésentation des filles dans un lycée ou la réussite est élevée.
Un autre exemple est une explication indexée historiquement et socialement tirée de Le raisonnement sociologique publié en 2006 par Passeron. Dans cet exemple, on a le cas paradoxal de la réussite différentielle des étudiants de différentes origines sociales à l’université en France, où les taux de réussite par cycle seraient les suivant :
En 1er et 2ème cycles, les étudiants d’origine sociale supérieure réussissent mieux que les étudiants issus des classes populaires. En 3ème cycle, la tendance s’inverse : les étudiants d’origine populaire réussissent mieux que ceux des classes supérieures. Comment l’expliquer ? Quelle(s) conclusion(s) peut-on en tirer ?
L’effet de l’origine sociale sur le taux de réussite à l’université s’inscrit dans un processus temporel de sélection : on passe du 1er au 3e cycle. Les mesures effectuées l’ont été sur des populations prises à différents stades du processus de sélection (étapes successives d’un cursus scolaire).
Pour interpréter les relations observées de ces trois tableaux, il faut prendre en compte le fait – qui n’est pas visible dans les tableaux – que les populations d’origines sociales différentes sont progressivement sélectionnées tout au long du cursus avec une inégale sévérité selon l’origine sociale.
Ce qui permet de donner du sens à cette interprétation est le concept de « sur-/sous-sélection scolaire relative ». Les échantillons sont progressivement et inégalement biaisés par la sélection (inégales sévérité scolaire, passé scolaire, résidence, sexe, origine sociale, etc.) et l’orientation scolaire.
La contextualisation est importante pour l’interprétation. Il faut mobiliser des éléments extérieurs aux tableaux, ici la mortalité scolaire différentielle (selon l’origine sociale). Sans cela, l’interprétation des relations statistiques fournies par les trois tableaux croisés est erronée.
Une mauvaise interprétation est :
« L’origine sociale supérieure favorise la réussite scolaire dans les premiers cursus universitaire et devient défavorable quand il s’agit de compétences scolaires requises au plus haut niveau de cursus universitaire. »
Une bonne interprétation est :
« L’origine sociale populaire fait moins réussir au départ mais quand on isole de l’ensemble de leur cohorte les étudiants d’origine populaire qui au 3ème cycle n’ont pas été éliminés et qui ont, de ce fait été sur-sélectionnés, la relation est inversée dans la sous-cohorte des survivants d’origine populaire. »
Tableaux croisés : les droits de l’homme[modifier | modifier le wikicode]
Mitchell et McCormick dans Economic and Political Explanations of Human Rights Violations publié en 1988 s’intéressent à la question de savoir comment expliquer le recours, par exemple, à la torture. En simplifiant un de leur tableau (Mitchell et McCormick 1988, 489), on trouve les effectifs suivants (l’unité d’analyse est le pays).
Mitchell et McCormick ont contribué à la recherche sur le respect des droits de l’homme en apportant des explications économiques et politiques. Ils argumentent que le respect des droits de l’homme comprend différentes dimensions et pour mieux le comprendre, il faut tenir compte de celles-ci.
Tenant compte du fait que leur variable dépendante est ordinale (par exemple « torture » : « jamais » ou « rarement », « parfois », « souvent », « très souvent »), ils évaluent leurs hypothèses avec des tableaux croisés.
La variable dépendante est une ligne et la variable indépendante en colonne. Ici la relation est significative.
On peut se demander si les conditions d’application du Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Chi2} sont respectées.
Si on prend la ligne « very often », la relation est significative. Dans ce tableau il manque un coefficient d’association qui permettrait de facilement évaluer laquelle des deux relations est la plus forte.
Les pays colonisés par les anglais ont moins de chance de prendre des prisonniers politiques.
Les analyses de Mitchell et McCormick permettent de tenir compte du caractère ordinal de variable dépendante, ce qui n’était pas le cas dans les analyses de Henderson dans Conditions Affecting the Use of Political Repression publié en 1991.
Toutefois, l’évaluation des hypothèses posent quelques problèmes. Les auteurs montrent qu’à la fois le régime politique et le développement économique affecte le respect des droits de l’homme. En analysant l’effet (uniquement) du régime politique sur le respect des droits de l’homme, on ne contrôle pas par le niveau de développement économique. La conséquence est que notre inférence peut être biaisée.
Tableaux croisés : la paix libérale[modifier | modifier le wikicode]
En terme de recherches empiriques sur la paix libérale, les travaux de Babst dans Elective Governments - a Force for Peace publié en 1964, ceux de Small et Singer dans The war-proneness of democratic regimes, 1816-1965 publié en 1976, Libertarianism and International Violence de Rummel publié en 1983 et de Liberalism and World Politics de Doyle publié en 1986 ont initié toute une série de recherches faisant appel à des méthodes quantitatives.
Rummel collectionne des informations sur tous les conflits entre 1976 et 1980 et les présente sous forme de tableau. Toute une série de chercheurs se sont appuyés sur ce type d’approche, en améliorant les analyses, les données, etc. pour rendre l’inférence causale plus convaincante.
Rummel présente une proposition : « Libertarian systems mutually preclude violence (violence will occur between states only if at least one is nonlibertarian » dont il dérive une hypothèse déterministe (Rummel 1983, 38) : « Libertarian states have no violence between them » et lui oppose une hypothèse nulle : « Libertarian states have violence between them ».
Rummel présente pour la période 1976 – 1980 les informations suivantes :
et pour les dyades « contiguës » :
Mais est-ce que ce lien pourrait être dû au hasard ? Dans le cas présent on est face à une situation où la variable dépendante et la variable indépendante sont nominales (d’où la présentation les résultats sous forme de tableau croisé). Y a-t-il la possibilité de dire quelque chose concernant l’incertitude de l’inférence causale dans un tel contexte ?
Calculons les pourcentages en colonne :
S’il n’y avait pas de relation on devrait s’attendre à la distribution suivante :
Le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle chi-2} pour ce tableau est de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 9.11} avec Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p = 0.003} indiquant une relation statistiquement significative.
La régression logistique[modifier | modifier le wikicode]
Dans la modélisation d’une variable qualitative, on cherche à prédire la probabilité qu’un individu (observation) aura d’être classé dans l’une ou l’autre catégorie de la variable dépendante et de mesurer l’effet de facteurs explicatifs (variables catégorielles et/ou quantitatives) sur une variable dépendante catégorielle.
Un modèle de régression logistique permet de déterminer comment les variables indépendantes affectent la probabilité de la présence de la caractéristique ou que l’évènement se produise comme par exemple avoir voté, être en échec scolaire, être en guerre, etc.
Il y a plusieurs types de régression logistique :
- régression logistique binaire : la VD est dichotomique (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} , Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} ) ;
- régression logistique multinomiale : La VD est nominale ;
- régression logistique ordinale : la VD est ordinale.
Les variables indépendantes Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle X_1} , Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle X_2} , . . ., Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle X_p} , sont quantitatives et/ou qualitatives (nominales ou ordinales).
Par exemple, on cherche à expliquer le vote par le niveau de revenu. Le vote est une variable dichotomique (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} oui, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} non) et le revenu est une variable quantitative (revenu annuel en milliers de $).
L’équation du modèle de régression linéaire est :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle vote = 0.17 + 0.01 \times revenu}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle R^2 = 0.27} ; Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle N = 77}
Les observations peuvent prendre deux valeurs, vote (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} ) ou ne vote pas (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} ).
La moyenne des valeurs de la variable vote correspond à la proportion des répondants ayant voté.
Les valeurs prédites de la variable vote de notre modèle de régression linéaire représentent la probabilité que chaque répondant a voté (plutôt que de s’être abstenu) étant donné son revenu annuel.
La constante (quand le revenu est égal à 0) représente la probabilité qu’un individu i avec un revenu de 0 ait voté :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle P_i (vote) = 0.17 + 0.01 \times 0 = 0.17}
Un individu j avec le revenu annuel maximum de 134’000$ :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle P_j (vote) =0.17 + 0.01 \times 134 = 1.51 }
Le problème est que le résultat est impossible (estimation aberrante) car la probabilité Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle P_j} vote dépasse Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} .
Quand la VD est une variable dichotomique, l’ajustement linéaire n’est pas adéquat car les valeurs estimées (probabilités) de la VD par le modèle peuvent dépasser Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} et descendre en-dessous de 0 (les prédictions de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑦} peuvent être Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle > 1} ou Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle < 0} ), alors qu’une probabilité est confinée à l’intervalle [0 - 1].
La source du problème est que la relation entre la variable dichotomique vote et la variable revenu n’est pas une relation linéaire. Donc, l’ajustement par la régression linéaire n’est pas correct. Une solution est le modèle logit dit aussi logistique.
La régression logistique binomiale[modifier | modifier le wikicode]
De façon générale, une régression fournit des estimations pour la variable dépendante comprises entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle - ∞} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle + ∞} , alors que dans notre cas nous nous intéressons à une probabilité qui doit donc être comprise entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} .
Le problème est résolu en estimant le modèle avec la fonction logit :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle π = logit(p) = log (\frac{P}{1 - p})}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -∞ < π < ∞}
La lettre grecque pi (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle π} ) est appelé le logit de la probabilité Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} qui est le logarithme de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} sur Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1 – p} .
Le modèle de régression logistique estime la probabilité de la valeur Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} par rapport à celle de la valeur Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} .
La probabilité de y d’être Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} (présence de la caractéristique ou de l’évènement, comme le fait de voter) s’écrit :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p = prob (y = 1)}
La probabilité de y d’être Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} (absence de la caractéristique ou de l’évènement, comme le fait de ne pas voter) s’écrit :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle q = prob (y = 0) = 1 - p}
L’équation de régression logistique est comme suit :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle π = logit(p )= log (\frac{P}{1 - p}) = β_0 + β_1 \times x_1 + ⋯ + β_k \times x_k}
En termes de probabilités, après transformation, l’équation s’écrit :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p = \frac {exp^{logit(p)}}{1 +exp^{logit(p)}} = \frac{exp^{(β_0 + β_1 \times x_1 + ⋯ + β_k \times x_k)}}{ 1 + exp^{(β_0 + β_1 \times x_1 + ⋯ + β_k \times x_k)}} = \frac{1}{1+ exp^{-(β_0 + β_1 \times x_1 + ⋯ + β_k \times x_k)}}}
Si sur le schéma de gauche, on a une probabilité de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0,5} alors le logit de cette probabilité correspond à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} . Si le fait d’être un homme produit une probabilité de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0,5} , soit de une chance sur deux, on ne peut pas affirmer que le fait d’être un homme influe la probabilité de voter. Si le fait d’être un homme produit une probabilité de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0,4} , le logit serait de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -0,41} . Cela signifie qu’il y a un effet négatif du fait d’être un homme sur la probabilité de voter. Si le fait d’être un homme prédit une probabilité de voter de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0,9} , le logit serait Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0,2} . Quand on a un logit de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} , il n’y a pas d’effet. Plus la probabilité de voter est proche de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} et plus le logit prendra une valeur négative élevée, et plus la probabilité de voter est proche de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} , plus le logit prendra une valeur positive élevée.
Le graphe de droite est une . C’est ce type de courbe qui ajuste correctement la probabilité qu’une évènement se produise et donc qui ajuste correctement une variable dichotomique. Le lien entre le logit et la probabilité est qu’on passe d’un intervalle [0,1] a des valeurs qui en sont pas bordée allant de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle - ∞} à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle + ∞} .
Ce graphe rend compte d’une droit de régression qui va permettre d’estimer une probabilité et qui estimera des probabilités qui ne dépasseront pas ou qui ne descendront pas en dessous de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} .
Les points représentent la moyenne des valeurs observées de vote pour chaque valeur de revenu.
Les courbes logistiques (en forme de S) appartiennent à la famille des courbes non linéaires exponentielles de forme générale :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Y_i = αe^{βX_i} + ε_i}
où :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle α} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle β} : les paramètres ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle ε} : le résidu ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle e} : une constante égale à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 2.718} ..., la base du logarithme nature.
Les coefficients (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle B} ) mesurent l’effet additif de chaque variable sur le logit. Il s’agit de l’effet toutes choses égales par ailleurs, c’est-à-dire lorsque les autres variables restent fixes :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle B = 0} indique indépendance statistique ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle B > 0} indique un effet positif de la variable sur le logit ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle B < 0} indique un effet négatif de la variable sur le logit.
Situation de référence : individu âgé de 0 ans et ayant un niveau de formation obligatoire Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Edulvl3(1)} = secondaire ; Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Edulvl3(2)} = tertiaire
- Le coefficient agea (âge) = Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.033}
Une année supplémentaire augmente le logit de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.033} , toutes choses égales par ailleurs (10 années de plus augmente le logit de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.33} )
- Les coefficients de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle edulvl3(1)} (secondaire) = Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.686} et de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle eduvlvl3(2) = 1.819}
Avoir un niveau d’éducation secondaire plutôt qu’un niveau obligatoire, le logit est, à âge égal, supérieur de 0.686.
Avoir un niveau d’éducation tertiaire plutôt qu’un niveau obligatoire fait augmenter le logit, toutes choses égales par ailleurs, de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1.819} .
L’exponentiel du coefficient (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Exp(B)} ), donne l’effet multiplicatif sur l’odds (la cote) Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {p}{(1 - p}} . L’interprétation se fait comme suit :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Exp(B) = \frac {rapport\ des\ odds}{cotes} = odds\ ratio}
L’odds ratio est le facteur par lequel l’odds (la cote) est multiplié lorsque Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle x_i} varie d’une unité et que les autres variables sont maintenues constantes.
ExpB :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle = 1} ⇒ pas de relation, indépendance (pas d’effet de la VI sur la VD)
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle > 1} ⇒ l’odds augmente (et donc la probabilité augmente)
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle < 1} ⇒ l’odds diminue (et donc la probabilité diminue)
La règle est que plus le coefficient s’approche de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} , plus la relation sera faible.
Les coefficients (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle B} ) sont le logarithme naturel de l’odds ratio (Log odds ratio)
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle B = Ln(Exp(B))}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Ln(1) = 0}
Un odds ratio (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Exp(B)} ) de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.2} traduit la même intensité d’association statistique qu’un odds ratio (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Exp(B)} ) de 5
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Ln(0.2) = –1.61}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Ln(5) = 1.61}
Par exemple, si on s’intéresse à l’effet de l’âge (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle agea} ) sur le vote :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle agea : exp^{0.033}= 1.033}
:
- pour une année de plus, l’odds est multiplié par Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1.033}
- pour 10 ans de plus, l’odds est multiplié par Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle exp(0.033 \times 10)}
- = Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle exp(0.33) = 1.391}
Pour une année de plus, les chances de voter plutôt que de ne pas voter augmentent de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1.033} .
Par exemple, si on s’intéresse à l’effet de l’éducation (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle edulvl3} ) sur le vote :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Edulvl3(1)}
(secondaire) : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle exp^{0.686} = 1.986}
- les chances de voter (plutôt que de ne pas voter) des personnes avec un niveau d’éducation secondaire sont environ 2 fois plus enlevées que les chances de voter des personnes avec un niveau de formation obligatoire.
Par exemple, si on s’intéresse à l’effet de l’éducation (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle edulvl3} ) sur le vote :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Edulvl3(2)}
(tertiaire) : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle exp^{1.819} = 6.169}
- les chances de voter (plutôt que de ne pas voter) des personnes avec un niveau d’éducation tertiaire sont environ 6 fois plus élevées que celles des personnes avec un niveau de formation obligatoire.
Avec un modèle de régression logistique on peut prédire la probabilité de voter Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑒𝑥𝑝logit(𝑝)} 1 Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {p} = \frac {exp^{logit(p)}}{1+exp^{logit(p)}} = \frac {1}{1+ exp^{-logit(p)}} = \frac {1}{1+ exp^{-(β_0 + β_1 \times x_1 + ⋯ + β_k \times x_k}}}
Si on s’intéresse à la probabilité de voter d’un individu de 30 ans avec un niveau de formation obligatoire, la prédiction de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} est comme suit : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {p} = \frac {1}{(1 + exp^{-(-1.862 + 0.033 \times 30}} = 0.2948} = 29%
Si on s’intéresse à la probabilité de voter d’un individu de 30 ans avec un niveau de formation tertiaire, la prédiction de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} est comme suit : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {p} = \frac{1}{1 + exp^{-(-1.862 + 0.033 \times 30 + 1.819}} = 0.7205} = 72%
Si on s’intéresse à la probabilité de voter d’un individu de 60 ans avec un niveau de formation tertiaire, la prédiction de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} est comme suit : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat {p} = \frac{1}{1+ exp^{-(-1.862 + 0.033 \times 60 + 1.819}} = 0.8740} = 87%
Les variables indépendantes catégorielles sont codées sous forme de variables auxiliaires Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle d_k} (qui sont des variables dichotomiques) : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle c} catégories ⇒ Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle c - 1} variables auxiliaires (dichotomiques)
Il y a différents codages (indicatrice ou contrastes) possibles. La façon de coder les variables catégorielles n’affecte pas la qualité du modèle et les estimations du logit et donc de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} mais affecte la valeur et l’interprétation des coefficients. Le codage est dicté par les hypothèses que l’on veut tester.
Le codage « indicatrice » est le plus facile à interpréter. On l’appelle aussi codage disjonctif.
Le codage « indicatrice » code la variable éducation Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle edulvl3} (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle c = 3} ), Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} = obligatoire, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 2} = secondaire, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 3} = tertiaire, avec les 2 variables auxiliaires Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle d_1} , Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle d_2} , définies ainsi :
Chaque Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle d_k} indique si l’on est (math>1</math>) ou non (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} ) dans l’état Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle k} . La dernière catégorie n’a pas de variable indicatrice explicite. Elle sert de « référence » et est caractérisée par une ligne de zéros dans la matrice de définition (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle design} ) des variables Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle d} . On peut changer la catégorie de référence.
Pour interpréter avec une un codage « indicatrice », on procède de la manière suivante : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle logit (p) = β_O + β_1 \times d_1 + β_2 \times d_2 = β_O + β_1 secondaire + β_2 tertiaire}
Pour la catégorie de référence Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle k = ref (= 1} ) : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle logit(p) = β_O}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle β_0} = logit à l’état de référence (obligatoire).
Pour les catégories Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle k ≠ ref} , Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle logit(p) = β_O + β_k}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle β_1} = écart entre logit en k et logit à l’état de référence.
Lorsqu’il y a plusieurs variables indépendantes, on parle aussi de situation de référence qui correspond à la valeur de la constante. Par exemple, avec 3 VI (éducation, âge centré sur la moyenne (43 ans), sexe), on a :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle logit (p) = β_O + β_1 secondaire + β_2 tertiaire + β_3 age_centre + β_4 femme}
Situation de référence : un homme, âgé de 43 ans, de niveau de formation obligatoire.
La forme générale du modèle de régression logistique est comme suit :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle logit(p(x_i )) = β_O + β_1 \times x_{i1} + β_2 \times x_{i2} + ⋯ + β_p \times x_{ip}}
où :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle x_{ij}} : valeur de la jème variable indépendante pour le cas Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle i} ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle x_i} : profil du cas Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle i} ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p(x_i) = p(y = 1/x_i)} : probabilité que la variable dépendante y prenne la valeur 1 pour un cas avec profil xi ;
Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle β_O} : constante du modèle ; Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle β_{j,j} = 1, ..., p} : coefficients des variables indépendantes.
Si on s’intéresse au vote selon le niveau d’éducation :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Odds_{uni} = \frac {p}{100 - p} = \frac {81.2}{100 – 81.2} = 4.3}
Parmi les universitaires les chances de voter sont 4.3 plus fortes que de ne pas voter [en utilisant les effectifs : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 310/72 = 4.3} ]
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Odds _{non.uni} = \frac {57.4}{100 – 57.4} = 1.3}
Parmi les non universitaires, les chances de voter sont 1.3 plus fortes que de ne pas voter [en utilisant les effectifs: Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {653}{485} = 1.3} ]
L’odds ratio est le rapport de deux odds, OR Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle = \frac{\frac {p}{1 - p}}{\frac {p}{1 - p}} = \frac {\frac {0.812}{1 - 0.812}}{\frac {0.574}{1 - 0.574}} = 3.2} . Les chances de voter plutôt que de s’abstenir sont 3.2 fois plus fortes pour les universitaires que pour les non universitaires.
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Coefficient B = Ln(odds ratio) = Ln(3.198) = 1.162}
La probabilité de voter d’un universitaire est :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \hat{p} = \frac {1}{1+ exp^{-(0.297+1.162)}} = 0.81137 ~ = 81.1%}
L’estimation du modèle est une procédure itérative basée sur le principe du maximum de vraisemblance qui constitue en quelque sorte le pendant pour la régression logistique de la méthode des moindres carrés pour la régression linéaire.
SPSS indique la déviance Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -2 ln\ L_m} (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -2\ Log\ Likelihood} ) d’un modèle Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle m} . La déviance Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -2\ ln\ Lm} s’interprète comme la distance entre les prédictions du modèle m et les observations. Plus le Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -2\ ln\ L_m} est petit, meilleur est l’ajustement. Le principe du test de significativité global (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle omnibus\ test} ) est qu’on teste si la différence de déviance entre le modèle Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle m} et le modèle Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle m_0} (avec constante seulement) est significativement significative. La statistique utilisée est la statistique du rapport de vraisemblance G2 appelée aussi déviance : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle G^2 (m_0 |m) =2\ ln\ L_m\ -2\ ln\ L_(m_0 ) ~ χ_{p}^{2}} où Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} est le nombre de paramètres sans la constante.
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle G2 m0|m =G^2 (m_0 |m) = 2\ ln\ L_m - 2\ ln\ L_(m_0 ) = 1011.294 - 969.035 = 42.58}
Plus généralement, les différences de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle -2\ ln\ L} de modèles imbriqués peuvent être assimilées à un Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle chi-2} . On peut donc tester la différence entre 2 modèles avec Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle G^2 (m_2 |m_1) = 2\ ln\ L_m - 2\ ln\ L_(m_0 ) ~χ_{c}^{2}} où Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle c} est la différence entre le nombre de paramètres.
Avec l’exemple de deux modèles imbriqués dans SPSS, on introduit dans une première étape l’éducation et l’âge puis dans une seconde étape le sexe :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle LOGISTIC\ REGRESSION\ VARIABLES\ parti2ch}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle /METHOD = ENTER\ edulvl3\ age_{c18}} →Block 1
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle /METHOD = ENTER\ gndr} →Block 2
Le chi-carré de maximum de vraisemblance du test de Hosmer et Lemeshow indique si les données sont compatibles avec le modèle. Ce test évalue la présence de différences significatives entre les valeurs observées et les valeurs prédites. On cherche donc à ce que ce test ne soit pas significatif. Ici, on inverse le processus normal de test statistique.
L’hypothèse nulle postule que les relations observées entre les variables dans l’échantillon sont conformes à l’existence des relations dans la population.
- Si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p > 0.05} : on ne rejette pas l’hypothèse nulle, on conclut que les données sont compatibles avec le modèle ;
- Si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p < 0.05} : on rejette l’hypothèse nulle, on conclut que les données ne sont pas compatibles avec le modèle (l’échantillon s’écarte de façon significative du modèle de relation postulé)
On cherche à ne pas rejeter l’hypothèse nulle, ce qui permet de conclure que les relations observées sont compatibles avec le modèle.
Le tableau de classification est un autre outil permettant d’évaluer la qualité d’ajustement du modèle. Il indique la proportion de cas dans l’échantillon qui seraient bien classés si on décidait de classer dans la catégorie 1 tous les cas dont la probabilité prédite d’appartenir à la catégorie 1 est supérieure à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.5} compte tenu de leurs valeurs sur les VI du modèle. Par défaut, le point de coupure est à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.5} .
Le tableau de classification permet d’évaluer la proportion des observations classées correctement par notre modèle. En principe, plus le pourcentage global d’observations classées correctement (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Overall\ Percentage} ) est élevé, meilleure est la qualité d’ajustement du modèle.
65.4% des observations sont classées correctement. Un modèle de régression logistique calcule la probabilité de voter pour la gauche pour les tranches supérieures.
| Probabilité de vote pour la gauche | Valeur prédit | Vote observée | |
| Individu 1 | 0,6 | 1 | 1 |
| Individu 2 | 0,4 | 0 | 0 |
| Individu 3 | 0,9 | 1 | 1 |
| Individu 4 | 0,49 | 0 | 1 |
| Individu 5 | 0,51 | 1 | 0 |
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle >0,5 → 1 = vote gauche}
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle ≤0,5 → 0}
La régression logistique n’a pas d’équivalent du Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle R^2} de la régression linéaire. Les pseudos R2 mesurent de l’utilité des variables explicatives dans le modèle mais non pas la qualité de l’ajustement :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle R^2} de Cox-Snell : n’atteint pas la valeur maximale théorique de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle R^2} de Nagelkerke : atteint la valeur maximale théorique de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} .
La statistique de Wald teste chacun des paramètres β de la régression logistique. L’hypothèse testée :
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle β_k = 0} ;
- Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_1} : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle β_k ≠ 0} ;
Si on ne peut pas rejeter Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle H_0} , on peut supprimer la variable correspondant au paramètre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle β_k} .
La catégorie de référence est le niveau obligatoire. Le test nous permet de nous dire si les individus qui ont un niveau de formation secondaire (deuxième ligne) se distinguent significativement dans leur probabilité de vote pour la gauche de leur catégorie de référence. Ici, le coefficient n’est pas significatif. Les personnes avec un niveau d’éducation secondaire ne se distinguent pas significativement des personnes au niveau obligatoire dans leur probabilité de voter pour un parti de gauche. La troisième ligne se compare également avec la ligne de référence. Le coefficient est significatif et donc on peut dire que les personnes du niveau tertiaire se différentient des personnes avec un niveau de formation obligatoire. Le coefficient Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle B} comme le test de significativité se fait par rapport à la catégorie de référence.
La régression logistique binomiale : la paix libérale[modifier | modifier le wikicode]
Retournant aux écrits de Kant, Cederman dans Back to Kant : Reinterpreting the Democratic Peace as a Macrohistorical Learning Process publié en 2001 propose des tests empiriques qui se rapprochent des thèses avancées par cet auteur. Quelles données et informations sont utilisées ?
Selon les réalistes, les deux arguments étaient que le bloc de l’ouest était démocratique et le bloc de l’est était non-démocratique. Le postulat est que c’était le fait que les États-Unis exercé un contrôle sur leur bloc tout comme l’URSS qui fait qu’il n’y a pas eu de conflit au sein de leur bloc. Selon Kant, les pays démocratiques apprennent beaucoup plus rapidement que les pays autoritaire le fait qu’il est plus viable de régler les conflits de façon paisible et non-violente. Pour Cederman, la diminution des disputes devrait être plus forte dans le cadre de pays démocratique.
Pour chaque année, Cederman a regardé le nombre de disputes dans des dyades entre pays démocratiques et des dyades entre des pays non-démocratiques. Les disputes dans les dyades démocratiques ont fortement diminuées. Il y a eu une augmentation puis une nouvelle diminution. Si on regarde dans les autres dyades, la probabilité de conflits et plus importante que pour les dyades démocratiques.
Le lien entre être une dyade démocratique et une dyade avec la probabilité qu’au moins un État soit non-démocratique; la variable dépendante est la probabilité que la dyade soit exposée à un conflit militarisé. Cederman chercher à savoir si la probabilité de dispute diminue avec le temps dans les dyades démocratiques.
Ces courbes montrent comment la probabilité de dispute augmente avec le temps. L’année est en horizontale et les probabilités de dispute sont sur l’axe vertical. Pour les dyades démocratiques, il y a une évolution négative la probabilité de conflit et pour les autres dyades la probabilité augmente avec le temps.
Jusqu’en 1860, les probabilités de conflit sont plus élevées pour les dyades démocratiques et à partir de 1870 c’est l’inverse qui se produit.
Ces analyses montre l’avantage de la régression logistique par rapport à l’utilisation des tableaux croisés.
Cedeeman ajoute d‘autres variables explicatives et essaie de montrer que les réalistes qui ont mis en doute la théorie de la paix libérale n’était pas du à la Guerre froide. Pour tester les arguments réalistes, il ajoute une indication pour savoir si une dyade est observe pendant la Guerre froide ou non. C’est une variable dichotomique qui prend une valeur de 1 si une dyade est obversé et 0 si ce n’est pas le cas.
Dans le premier modèle, il trouve un effet significatif de la Guerre froide mais ce qui importe le plus est que l’effet d’être une dyade démocratique est toujours significatif et toujours négatif. Ce résultat lui permet déjà d’invalider l’hypothèse des réalistes concernant la Guerre froide. Dans le deuxième modèle lorsqu’il contrôle entre la période la Guerre froide et celle de l’entre-deux-guerres, l’effet est négative pour les deux dyades.
Cederman a ajouté trois autres variables de contrôle à savoir les alliances, les capacités militaires et le développement économique. Lorsqu’il intègre ces trois autres de variables de contrôle, il regarde les variations.
Le premier coefficient correspond à la dyade démocratique, le coefficient est toujours négatif et significatif pour les deux modèles.
La courbe d’en bas représente les dyades démocratique, la deuxième courbe est par exemple la dyade entre la Suisse et l’Allemagne avec un probabilité de conflit qui diminue fortement avec le temps, ce sont des dyades démocratiques qui ne sont pas nature. La troisième courbe correspond aux nouvelles dyades. On voit qu’au cours de la période 1845 à 1990, une diminution du risque de conflit, toutefois le risque de conflit reste supérieur aux dyades mature ou de celle datant de 1848. Ces courbes sont calculées à partir des modèles précédents.
La régression logistique binomiale : les droits de l’homme[modifier | modifier le wikicode]
Toute une série de travaux essaient d’évaluer ce qui explique le respect des droits de l’homme, en tenant compte de différentes explications : régime politique, ratification de traité, capacité administrative, etc.
Wegmann, dans un travail de maîtrise intitulé Regional Human Rights Systems. A Comparative Analysis publié en 2012, s’intéresse essentiellement aux systèmes de mise en conformité (« compliance systems »). Wegmann utilise comme variable dépendante le « physical integrity index » de Cingranelli et Richards tiré de leur ouvrage The Cingranelli and Richards (CIRI) Human Rights Data Project publié en 2010, et le recode pour qu’il ne prenne que deux valeurs (pour pouvoir utiliser une régression logistique). Elle argumente que les effets des différentes variables devraient dépendre du respect (ou non) des droits de l’homme l’année précédente.
Une première analyse est une régression logistique. Sur la première ligne on toue l’effet de mise en conformité.
Il y a une variable dépendante supplémentaire qui est le nombre d’années qu’un pays n’a pas respecté les droits de l’homme.
Le travail de Wegmann illustre l’utilisation d’une régression logistique pour étudier un aspect du respect des droits de l’homme. Comme pour toute régression (ou analyse quantitative, voir qualitative) il faut s’interroger sur les postulats sous-jacents à ces analyses. D’autres travaux (voir par exemple Neumayer 2005, Hug et Wegmann 2012) utilisent également des régressions logistiques, mais puisque leur variable dépendante est ordinale (le “physical integrity index” de Cingranelli et Richards (2010)), ils se servent d’extensions de la régression logistique (binomiale), à savoir une régression logistique ordinale.
Construction d’un modèle de régression[modifier | modifier le wikicode]
Il existe plusieurs stratégies de modélisation et notamment trois types de modes d’entrées des VI
- standard : toutes les variables sont introduites simultanément ;
- séquentielle : les variables sont introduites par blocs successifs, chaque bloc comportant une ou plusieurs variables ;
- statistique : le logiciel choisit l'introduction ou l’élimination de chaque VI en fonction de critères statistiques.
- régression standard : toutes les VI sont entrées simultanément.
On estime la signification statistique de la contribution de chaque VI sous contrôle de toutes les autres VI permettant d’évaluer l’importance et la contribution de chaque VI sous contrôle de toutes les autres VI. C’est un mode d’entrée des variables peu satisfaisant pour des modèles sophistiqués. Sa limite est que la contribution unique des VI n'émerge que de manière générale, sans qu'on puisse étudier la logique de relation des variables. La régression standard ne permet pas d’évaluer, par exemple, s’il y a des effets directs et indirects d’une VI sur une VD ou s’il y a la possibilité d’une chaîne de relation causale (effet indirect d’une VI sur une VD).
- régression séquentielle : introduction des VI par blocs successifs.
Les VI sont introduites dans le modèle selon un ordre défini par le chercheur, par étapes successives. L’ordre d’entrée des VI résulte de considérations théoriques ou logiques, ou des hypothèses formulées, ce qui permet d’évaluer la valeur ajoutée des VI en termes de pouvoir explicative ou de qualité d’ajustement. La VI introduite à l’étape 2 doit avoir une valeur ajoutée à l’explication de la VD pour que le pouvoir explicatif ou la qualité d’ajustement augmente. Dans le cas d’une régression linaire, changement de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle R^2} indique l’apport unique de la VI qui a été ajoutée au modèle. La VI introduite à l’étape 2 doit avoir une valeur ajoutée pour que le changement de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle R^2} soit significatif.
Cette stratégie permet de répondre à des questions sur la contribution d’une VI ou d'un ensemble de VI au-delà de la contribution des VI qui sont déjà dans le modèle et permet de répondre à des questions théoriques du type, par exemple, est-ce que l'âge explique la motivation au travail au-delà de l’ancienneté dans l’organisation, est-ce que les valeurs politiques expliquent le refus d’adhésion des Suisses à l’Union européenne au-delà de la contribution des variables sociodémographiques ou encore est-ce que de faibles relations économiques expliquent les guerres au-delà du type de régime politique ? Elle permet aussi de tester des hypothèses théoriques spécifiques concernant, par exemple, l’existence de médiation entre les variables. Des hypothèses précises peuvent être testées à propos de l’effet des VI (coefficients de régression des VI) qui peuvent changer suite à l’introduction d’autres VI dans le modèle. La valeur du coefficient peut augmenter ou diminuer, le signe peut s’inverser, le coefficient peut devenir significatif ou non significatif.
- Régression statistique : le logiciel choisit l’introduction/élimination de chaque VI en fonction de critères statistiques.
Il existe différents types de régression statistique. Les critères statistiques la régression linéaire à savoir la probabilité statistique de signification du coefficient b et la régression logistique, c’est-à-dire la probabilité statistique de signification du coefficient b mais différents tests peuvent entre utilisés : Wald, LR, etc. C’est une méthode pas recommandée pour tester des hypothèses. Elle est donc à utiliser uniquement pour des analyses exploratoires.
Si, dans le modèle final, il y a les mêmes variables indépendantes, les coefficients de régression seront les mêmes quelle que soit la méthode utilisée. Ce qui différencie ces trois méthodes est l'ordre d'entrée des variables et le type de questions auxquelles elles permettent de répondre. Selon la méthode utilisée, on peut aboutir à un modèle final diffèrent. Il faut privilégier le modèle théorique plutôt que des considérations purement statistiques. Donc, la préférence va à la régression séquentielle.
On cherche à tester l’hypothèse d’une relation causale entre le degré de religiosité et le niveau de conservatisme : plus on est religieux, plus on est conservateur. Le niveau de conservatisme correspond à la variable ccon100 qui est un variable d’intervalles représenté par une régression linaire Pour tester cette hypothèse, on va introduire les VI dans le modèle en 4 étapes (on pourrait choisir d’autres VI ou introduire seulement 2 blocs) :
- 1ère étape : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle rlgdgr} ;
- 2ème étape : campagne, femme, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle age_c18} ;
- 3ème étape : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle eduyrs} , Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle pereuni} ;
- 4ème étape : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle lrscale} .
Ce tableau résume les stratégies de modélisation séquentielles.
On obtient un Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle R^2} pour chacun des bloc ainsi que le changement du Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle R^2} .
L’hypothèse d’une relation causale entre le degré de religieuse et le niveau de conservatisme est vérifiée.
Dans le cadre d’une stratégique de modélisation séquentielle, on cherche à tester l’hypothèse d’une relation causale entre le genre et la participation politique : les femmes votent moins que les hommes. La participation politique est représenté par la variable Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle vote2} qui est une variable dichotomique (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} abstention, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} vote) régression logistique binaire.
Pour tester cette hypothèse, on va introduire les VI dans le modèle en 4 étapes :
- 1ère étape : femme (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} homme, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} femme)
- 2ème étape : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle age_c18} (années, centré sur 18 ans : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 18 ans = 0} )
- 3ème étape : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle edulvl3} (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} obligatoire, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 2} secondaire, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 3} tertiaire)
- 4ème étape : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle classesup} (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} classes populaires, Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} classes moyennes/sup.
- madi stratégie séquentielle de modélisation Régression logistique bloc 1.png
BLOC 1 : dans le modèle avec uniquement le sexe comme VI, le coefficient Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle b} indique un effet négatif et significatif du fait d’être une femme sur la participation politique.
- madi stratégie séquentielle de modélisation Régression logistique bloc 2.png
BLOC 2 : l’introduction de l’âge renforce légèrement l’effet négatif du sexe sur la participation.
- madi stratégie séquentielle de modélisation Régression logistique bloc 3.png
BLOC 3 : l’effet négatif du fait d’être une femme sur la participation disparaît lorsque l’on introduit le niveau de formation : le coefficient Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle b} pour les femmes devient non significatif.
- madi stratégie séquentielle de modélisation Régression logistique bloc 4.png
BLOC 4 : l’introduction de la classe sociale ne change rien. Elle fait légèrement diminuer l’effet de l’éducation sur la participation politique.
On peut conclure soit à une relation fallacieuse, soit à une relation de causalité type chaine de relation. La chaîne de relation est sexe → éducation → participation politique. L’effet négatif du sexe sur la participation politique observé au niveau bivarié (bloc 1) est dû au fait que les femmes disposent, en moyenne, d’un niveau de formation inférieur à celui des hommes (elles sont surreprésentées dans les bas niveaux de formation). Il y a un effet indirect du sexe sur la participation politique et l’éducation est une variable intermédiaire.
Le processus de construction d’un modèle de régression vise à réaliser une régression standard pour examiner la contribution unique de chaque variable et la variance partagée dans l’explication de la VD, mais aussi à faire une régression séquentielle en fonction du modèle théorique postulé. Il faut donc avoir élaboré un modèle théorique ou des hypothèses et réaliser une régression parcimonieuse où seules les variables indépendantes significatives sont gardées (surtout pour la régression logistique).
La construction d’échelles[modifier | modifier le wikicode]
Introduction à la construction et d’échelles additives[modifier | modifier le wikicode]
Les échelles sont utilisées en sciences sociales pour mesurer des concepts abstraits ou complexes comme par exemple, l’anomie, le post-matérialisme, l’aliénations sociale ou encore la démocratie.
Il y a différents types d’échelles :
- échelles « conceptuelles » comme par exemple le post-matérialisme ou le niveau de démocratie ;
- création d’échelles ad hoc comme l’activisme politique : en combinant les différentes réponses à ces questions, il est possible de construire des échelles comme par exemple celle de l’activisme politique.
- catalogues d’échelles : combinaison de différents facteurs cherchant à mesurer un phénomène. Ce sont des indices ou encore nomenclatures comme les catégories socioprofessionnelles, l’indice de prestige de Treiman, l’indice de développement humain (IDH) ou encore les tests de QI qui est un résultat d'un test psychométrique.
On distingue deux types d’échelles à savoir les échelles unidimensionnelles et les échelles multidimensionnelles.
Par exemple, on cherche à mesurer l’intérêt pour la politique :
- SI le concept est unidimensionnel on va créer une échelle unidimensionnelle (indicateur synthétique) : à partir d’une série d’indicateurs appelés « manifestes » parce que mesurer directement par des enquêtes par sondage. On construit des indicateurs synthétiques qui sont supposés mesurer l’intérêt pour la politique, c’est-à-dire le concept.
- Si le concept est multidimensionnel : on va créer plusieurs échelles. On passe d’un indicateur manifeste pour construire un indicateur latent qui est censé mesurer le concept.
L’échelle doit être utile et pertinente pour la construite dans l’analyse. L’échelle peut être utilisée comme VD ou comme VI, elle doit discriminer des groupes ou être un bon facteur explicatif. C’est l’une des manières de valider l’échelle dans l’analyse.
En sciences sociales, on cherche à mesurer des attitudes qui sont des caractéristiques individuelles profondes ou prédisposition acquise plus ou moins stables qui permettent d’expliquer des comportements comme par exemple le leadership d’opinion ou encore le conformisme. Les attitudes sont un phénomène complexe difficile à saisir via des questions directes ou des indicateurs simples.
On cherche à mesurer des phénomènes avec un ensemble d’indicateurs (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle i_1} , Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle i_2} , Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle i_3} , etc.) considères comme aisément mesurables
Ce processus de passage d’une série d’indicateurs simples vers un indicateur complexe (synthétique) est appelé construction d’une échelle.
Les étapes d’une construction d’échelle sont au nombre de quatre :
- Construction théorique du phénomène mesuré : définition du concept à savoir quelle caractéristique profonde veut-on analyser ;
- Choix des indicateurs (variables) appropries pour mesurer ce phénomène : souvent limité aux variables disponibles dans les fichiers de données. On va mettre en place une analyse univariée de ces indicateurs ;
- Création de l’échelle : elle n’est rien d’autre qu’une nouvelle variable mesurant empiriquement l’attitude ou le phénomène ;
- Diagnostic de la nouvelle variable créée : il faut se poser la question qui est de savoir si l'échelle correspond-t-elle à la dimension théorique qu'on voulait capter. Par exemple, l’échelle mesurant le degré de démocratie mais toutes les observations se placent soit dans les valeurs basses, soit dans les valeur élevées.
Concernant l’exemple de la mesure du leadership d’opinion, les postulats théoriques sont posé par Lazarsfeld dans The People’s Choice: How The Voter Makes Up His Mind in a Presidential Campaign publié en 1944 et dans Personal influence: The part played by people in the flow of mass communications publié en 1955 de Katz et Lazarsfeld. Ces auteurs aborde la théorie de la communication à deux étages (two-step flow of communication).
Il existe une élite de personnes occupant une position essentielle dans les processus communicationnels. Ces personnes sont bien informés sur les sujets politique et transmettent leur connaissance aux personnes de leur entourage (au sens large). Ce sont des leaders d’opinion. L'influence des medias sur les citoyens se fait donc en deux temps .
Les leaders d'opinion se caractérisent par divers traits. Ils paraissent mieux informés que les personnes de leur entourage, ils sont plus attentifs aux informations, ils lisent beaucoup de journaux, écoutent la radio et regardent notamment la télévision. Pour Schwartzenberg dans Politique mensonge publié en 1998, « Les idées se répandent à partir de la radio et de la presse aux leaders d'opinion, et ensuite de ceux-ci aux sections moins actives [...]. Ainsi, les leaders d'opinion médiatisent l'influence des mass medias sur les individus ».
Comment mesurer le concept de leadership d’opinion ? Soit par une question directe comme « êtes-vous un leader d’opinion ? » mais ce n’est pas la bonne méthode, soit en utilisant plusieurs indicateurs mais il faut savoir lesquels.
Katz et Lazarsfeld proposent d’utiliser les deux indicateurs suivants à savoir si l’individu discute-t-il de politique et arrive-t-il a convaincre son entourage de ses positions. Le postulat de base est que les individus qui discutent souvent de politique et qui arrivent souvent à convaincre leur entourage sont des leaders d’opinion.
On va procéder par des Analyses VOX qui sont des enquêtes par sondage réalisée après chaque votation. Deux types de questions vont être posées :
- À quelle fréquence vous arrive-t-il de discuter de questions politiques avec des amis ou connaissances ? Est-ce souvent, rarement ou jamais le cas? (variable: polit). Les modalités de réponse vont être : (1) souvent; (2) rarement; (3) jamais; (4) indécis; (5) pas de réponse.
- Lorsque vous avez une conviction profonde dans une affaire politique, vous arrive-t-il de convaincre vos amis, parents ou connaissances de partager votre point de vue? Est-ce souvent, rarement ou jamais le cas ? (variable: politu). Les modalités de réponse vont être : (1) souvent; (2) rarement; (3) jamais; (4) indécis; (5) pas de réponse.
À partir de ces deux questions, il y a différentes manière de construire des échelles. L’opérationnalisation est la traduction empirique qui est le passage du modèle théorique au modèle empirique.
Ici, on met plus de poids au fait de convaincre son entourage.
Dans le tableau croisé, les leaders d’opinion sont représentés par les deux cellules encadrées.
La deuxième proposition d’opérationnalisation serait une échelle qui mesure différents niveaux de leadership. C’est une échelle continue allant de « 1 », « leader » à « 5 », « non-leader ». Est proposé une échelle ordinale (qu’on pourrait supposer métrique) qui mesure le degré de leadership. L’attribution est un peu arbitraire.
Toute les fois ou apparait 5, les individus ne sont pas leader d’opinion.
Il est possible de construire deux échelles assez différentes. Il y a une marge de manœuvre interprétative afin de construire ces échelles et les résultats ne sont pas tout à fait pareil.
On a une échelle dichotomique ordinale l’autre étant ordinal métrique.
L’échelle post-matérialiste est une échelle conceptuelle. Les postulats théoriques proviennent de l’ouvrage de Inglehart intitulé The Silent Revolution publié en 1977.
Après mai 1968, un profond changement dans les priorités des valeurs des individus. Il postule un changement irréversible des priorités de valeurs dans les sociétés postindustrielles. Les valeurs à la base de nos sociétés sont en train de changer graduellement : on assiste à un glissement de valeurs purement matérialistes (ordre, sûreté économique, tranquillité, etc.) vers des valeurs dites post-matérialistes centrées sur l’autonomie et l’expression individuelle (participation citoyenne, liberté d'expression, écologie, démocratie, etc.) Cela s'insère dans un projet global d'analyse comparative des valeurs nommé World Value Surveys. Depuis 1990, des enquêtes par sondage sont réalisées à l'échelle mondiale en vagues successives.
Comment mesurer les valeurs matérialistes et les valeurs post-matérialistes ? Inglehart propose d’utiliser les deux questions suivantes, posées aux individus :
- Parmi les buts figurant sur cette liste, pourriez-vous m'indiquer celui qui vous paraît le plus important pour les années à venir ? « maintenir l'ordre dans le pays », « augmenter la participation des citoyens », « combattre la hausse des prix » et « garantir la libre expression »..
- ...et celui qui vient ensuite (le deuxième plus important) ?
Les différents buts proposés font référence à deux dimensions sous-jacentes et opposées :
- matérialisme : l’ordre, la sûreté économique, la tranquillité comme maintenir l'ordre dans le pays ou combattre la hausse des prix.
- post-matérialisme : la participation citoyenne, la liberté d'expression, l’écologie ou encore la démocratie comme augmenter la participation des citoyens ou garantir la libre expression.
Inglehart combine ces deux indicateurs. Selon les combinaisons on va attribuer un qualificatif. L’utilité d’une échelle se trouve dans l’analyse qu’on va en faire.
« 1 », « matérialiste » ; « 2 », « plutôt matérialiste » ; « 3 », « plutôt post-matérialiste » ; « 4 », « post-matérialiste ».
La théorie indique parfois comment mesurer le concept comme avec Inglehart, Lazarsfeld et Katz. Mais c'est au chercheur de décider la forme de la nouvelle variable. Les choix opérés influencent le résultat obtenu (la mesure de l’indicateur), les analyses et les conclusions de la recherche.
Différents indicateurs mesurables peuvent être additionnés pour mesurer empiriquement l'attitude ou le phénomène étudié. Ces différents indicateurs doivent être liés entre eux par un concept théorique commun ce qui rend leur cumul théoriquement acceptable.
La propriété d’une échelle additive est que les items (indicateurs) sont substituables. On postule l’unidimensionnalité à moins que l’échelle corresponde à une dimension d’un concept. Il y a des possibilités de mesurer empiriquement le lien entre les indicateurs que l’on appelle une analyse de fiabilité (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Reliability} ).
L’analyse de fiabilité permet de déterminer jusqu'à quel point chacun des items (variables) constituant une mesure équivalente d'un même concept. Lorsqu’on procède à la construction d’une échelle additive, on devrait précéder à la construction d’une analyse de fiabilité.
On a un ensemble d’items, une batterie de question renvoyant à ce qu’on peut appeler l’activisme politique.
On va chercher à mesurer l’activisme politique des individus. Pour cela, on va construire une échelle additive d’activisme politique en additionnant les scores des individus pour chacune des actions politiques proposées. Il faut avoir en tête le codage de chacun des items. Les valeurs (codage) de chaque item sont « 2 », « Déjà fait » ; « 1 », « Pourrait faire » ; « 0 », « Jamais ».
Les individus ayant déjà fait toutes ces actions obtiennent le score maximal d'activisme politique : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 2 \times 8} ; actions = Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 16} . Les individus n’ayant jamais rien fait (et refusent de le faire) obtiennent le score minimal d'activisme politique Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 0 \times 8} actions = Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} . C’est à partir de la fabrication des indicateurs qu’on va donner un score.
La création d'une échelle additive d’activisme politique varie théoriquement de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 16} . On obtient une échelle quantitative d’intervalles.
La procédure Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RELIABILITY} permet de vérifier la cohérence entre les items composant l'échelle, la relation statistique entre les items composant l'échelle (corrélation) et la relation statistique entre chaque item et la future échelle. C’est une analyse préalable qui ne construit en rien l’échelle. Cette analyse de fiabilité permet de déterminer les items que l’on va retenir afin de construire l’échelle additive.
L’Alpha de Cronbach est un coefficient qui indique la qualité globale de l'échelle par rapport aux items qui la composent (mesure de la cohérence interne de l’échelle). C’est une résumé standardisé entre Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} . Sur le plan statistique, on recherche une valeur supérieure à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.7} qui est le seuil conventionnel à partir du quel la mesure est de bonne qualité.
La matrice de corrélation entre les items correspond aux corrélations simples (relations bivariées). Tous les items doivent être corrélés les uns avec les autres et toutes les corrélations doivent être positives. Si la relation(s) est négative(s), soit l’item(s) qui ne contribue(nt) pas à l’échelle, soit il y a un problème de codage (polarité inversée).
- Corrected item-Total Correlation : une corrélation forte indique une forte contribution de l'item à l'échelle finale ;
- Alpha si l’item est éliminé : calcul de l'Alpha de Cronbach de l'échelle sans l'item en question ;
- Si l’Alpha est supérieur à l’Alpha de l’échelle initiale (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle α = 0.704} ), on peut choisir, sur la base de ce critère statistique, d’éliminer l’item en question
Il faut bien vérifier la direction de la corrélation entre les items, ainsi que son intensité mais aussi éliminer un item à la fois puis répéter la procédure depuis le début (relancer une analyse de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RELIABILITY} ). L'échelle finale n'est pas construite par la procédure Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle RELIABILITY} (c'est à vous de le faire ensuite). Mais surtout, il faut s'assurer que la construction de l'échelle ait un sens théorique.
Si un individu à répond à toutes les question sauf une, il est exclus mais on a quand même une idée de son potentiel d’activisme.
Sur l’axe vertical, il y a les valeurs allant de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 16} étant les valeurs de l‘échelle additive d’activisme. La boite comporte 50% des observations et la médiane est la ligne dans la boite. La médiane est autour de 4. Chaque patte comporte 25% des observations. Il y a une concentration des individus vers le bas de l’échelle, n’étant pas une observation symétrique. 50% des individus ont un niveau d’activisme à 4.
Après avoir étudié la fiabilité de l’échelle, puis l’avoir construite, on peut l’utiliser dans les analyses soit comme VD soit comme VI. L’hypothèse est que « plus l’intérêt pour la politique est élevé, plus l’individu sera actif politiquement ». L’échelle obtenue est une variable intervalle quantitative. On va utiliser des tableaux de moyennes pour vérifier notre hypothèse car ils sont appropriés pour analyser une relation entre une variable indépendante qualitative et une variable dépendante quantitative.
Le projet « Transitions et caractéristiques des régimes politiques, 1800 – 2013 » est mis en œuvre par POLITYTM IV PROJECT. C’est une base de donnée constitué entre 1800 et 2013 avec un certains nombre d’indicateurs dont le niveau de démocratie. Est mesuré le niveau de démocratie des pays auxquels est attribué un score sur l’échelle de démocratie pour tous les pays chaque année depuis 1800.
Les quatre indicateurs utilisés sont la « compétitivité de la participation politique », l’« ouverture du recrutement de l’exécutif », la « compétitivité du recrutement de l’exécutif » et la « contraintes sur le chef de l’exécutif ». L’échelle utilisée est une échelle additive pondérée. Le score varie de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 10} .
Chaque pays a une valeur allant de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 4} . Pour chaque pays à chaque année on attribut un score. Ces scores sont additionnés avec un maximum de 10. Leur construction des indicateurs et le poids attribué à chacune des caractéristiques reste arbitraire.
Le concept mesuré doit avoir un fondement théorique. L'opérationnalisation se fonde sur un choix cohérent d'indicateurs présents dans le fichier de données. Les indicateurs peuvent provenir de la théorie comme par exemple le post-matérialisme ou d'une analyse exploratoire étudiant le lien mutuel entre les indicateurs afin d'établir la fiabilité de l'échelle (analyse RELIABILITY). Il faut toujours produire des analyses exploratoires de vos indicateurs (analyses univariées).
L’analyse factorielle[modifier | modifier le wikicode]
L’analyse factorielle est terme générique désignant un ensemble de techniques statistiques :
- analyse en composantes principales (ACP) ;
- analyse factorielle des « psychologues » ;
- analyse des correspondances (AC);
- analyses des correspondances multiples (ACM)
D’autres techniques statistiques dérivent de ces techniques.
Il y a trois utilisations principales de l’analyse factorielle :
- comprendre la structure de relation d’un ensemble de variables comme par exemple comprendre la structure de la variable latente « intelligence » ;
- l’analyse factorielle est un moyen pour « mesurer » des concepts qui ne sont pas directement mesurables, c’est-à-dire une variable latente. C’est la démarche typique des constructions d’échelles. Par exemple, les concepts qu’on peut chercher à mesure à l’aide d’une analyse factorielle seraient la tolérance, le racisme, la satisfaction au travail ou encore l’ouverture ;
- réduire un nombre important d’informations (prenant la forme de variables) à quelques grandes dimensions (échelles) : ces informations prennent la forme de variables et on obtiendra des échelles.
On chercher à expliquer la plus forte proportion de la variance (ou de la covariance) par un nombre aussi restreint que possible de variables appelées composantes, facteurs ou dimension mais aussi à fournir des représentations synthétiques sous forme de visualisations graphiques, tout comme donner une image simplifiée des multiples relations entre les variables et entre individus et variables. Ces techniques permettent de créer des échelles.
Le terme de variables latentes désigne ces variables qui existent au plan conceptuel et qui ne sont pas directement mesurées. Les composantes/facteurs produits par l’analyse factorielle sont ces variables latentes On suppose qu’une dimension générale existe et que le positionnement des individus par rapport à cette dimension (variable latente) explique/prédit leur positionnement sur chacune des variables mesurées. C’est par exemple le modèle éducatif (vision de l’éducation/normes éducatives) que les individus ont qui va déterminer si les principales qualités à transmettre aux enfants sont l’obéissance et le respect les règles ou plutôt la créativité. Les réponses aux questions sur les qualités à transmettre aux enfants nous permettent de dégager le principe explicatif qui n’est pas mesurable directement.
Il y a différents types de questions auxquelles les analyses factorielles permettent de répondre :
- combien de facteurs sont nécessaires pour donner une représentation juste et parcimonieuse des données ?
- quelle est la nature de ces facteurs, comment peut-on les interpréter ?
- quelle proportion de la variance des données peut être expliquée par un certain nombre de dimensions (facteurs) majeures ?
- jusqu'à quel point la solution factorielle est conforme à la théorie que je voulais vérifier ?
- la structure factorielle est-elle la même pour divers groupes ?
Pour dépend du niveau de mesure des variables on en revient au niveau de mesure :
- analyse en composante principale (ACP) : variables quantitatives ou ordinales métriques ;
- analyse factorielle des « psychologues » : variables quantitatives ou ordinales métriques ;
- analyse des correspondances (AC) : deux variables qualitatives qui peuvent être ordinales ou cardinales ;
- analyse des correspondances multiples (ACM) : plusieurs variables qualitatives.
Les analyses multidimensionnelles permettent de résumer un phénomène à l'aide de plusieurs dimensions. Les diverses variantes de l’analyse factorielle permettent de créer des échelles. Plusieurs dimensions, facteurs ou composantes sont extraites pouvant être utilisés comme des échelles. L’analyse factorielle permet d’évaluer le nombre de dimensions requises pour mesurer un phénomène et permet également une approche inductive lorsque le phénomène n’est pas connu ainsi que de découvrir les dimensions sous-jacentes à un ensemble de variables.
La variance totale pour une variable a deux composantes :
- une partie est partagée avec d’autres variables : variance commune ;
- une autre partie est spécifique à cette variable : variance unique.
Par exemple, il y a une relation entre 3 variables à savoir Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle x} , Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle y} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle z} . La partie hachurée est la variance. La zone commune et la partie non hachurée est la variance unique de chaque variable.
L’analyse en composante principale cherche une solution à l’ensemble de la variance des variables mesurées (variance commune et unique). Les composantes sont orthogonales entre elles, c’est-à-dire indépendantes. Elle cherche à maximiser la variance expliquée.
L’analyse factorielle des psychologues cherche une solution à la covariance entre les variables mesurées (variance commune). Elle tente d’expliquer seulement la variance qui est commune à au moins deux variables et présume que chaque variable possède aussi une variance unique représentant son apport propre. Les divers modes d’extraction visent à maximiser une bonne reproduction de la matrice de corrélations originale.
Pour qu’une variable soit intégrée dans l’analyse, sa distribution doit montrer une certaine variance, c’est-à-dire elle doit discriminer les positions des individus. Idéalement, on cherche une structure simple, c’est-à-dire une solution où chaque variable est fortement liée à un seul facteur. Lorsqu’une variable est corrélée à plus d’un facteur, on dit que c'est une variable complexe ; on peut dire que la signification des réponses à cette variable s'interprète selon plusieurs dimensions. La structure factorielle peut être différente pour différentes populations. Il faut faire attention à ne pas regrouper pour l’analyse des populations trop différentes. Pour qu’une structure factorielle soit stable, elle doit avoir été vérifiée sur un minimum de cas. La règle veut qu'il y ait un minimum de 5 cas par variable.
Les variables utilisées pour l’analyse devraient se distribuer normalement avec des variables quantitatives. Lorsqu’on utilise l’analyse factorielle, il est possible de transgresser cette règle en utilisant une procédure d'extraction (Unweighted least square ou ULS) qui tient compte du fait que la distribution des variables n’est pas normale (notamment quand on utilise des variables ordinales). La relation entre les paires de variables est présumée linéaire. Toutes les variables doivent faire partie de la solution c’est-à- dire être corrélées minimalement avec une ou plusieurs dimensions, sinon elles doivent être retirées de l'analyse puisqu’elles n’appartiennent pas à la solution factorielle
Pour une extraction de type PC pour principal component, on utilise une analyse en composantes principales et pour une extraction pour l'analyse factorielle, il y a plusieurs méthodes d'extractions. Lorsque la solution factorielle est stable, les diverses méthodes donnent des résultats identiques ou du moins similaires :
- ML (maximum likelihood, c’est-à-dire maximum de vraisemblance) : maximise la probabilité que la matrice de corrélation reflète une distribution dans la population. Cette méthode produit aussi un test de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle χ^2} de rapport de vraisemblance qui indique si la solution factorielle est plausible. La probabilité de ce test doit être supérieure à 0.05, c'est-à-dire que l'on ne doit pas rejeter l'hypothèse nulle qui veut que le modèle soit compatible avec les données. C’est une méthode sensible aux déviations à la normalité des distributions. Cette méthode rencontre souvent des problèmes avec des échelles ordinales de type très, assez, peu, pas du tout ;
- ULS (unweighted least square ou moindres carrés non pondérés) : minimise les résidus. C’est la méthode privilégiée lorsque les échelles de mesure sont ordinales ou que la distribution des variables n'est pas normale. C’est une situation fréquente en sciences sociales, notamment quand on mesure des attitudes ;
- Alpha : méthode pertinente quand on cherche à créer des échelles car elle tente de maximiser l'homogénéité à l'intérieur de chaque facteur et ainsi la fiabilité.
La rotation est le processus mathématique qui permet de faciliter l'interprétation des facteurs en maximisant les saturations (corrélations) les plus fortes et en minimisant les plus faibles de sorte que chaque facteur apparaisse déterminé par un ensemble restreint et unique de variables. Ce processus est effectué par rotation, c’est-à-dire par un repositionnement des axes.
L’idée de la rotation est de repositionner les deux axes qui sont toujours orthogonaux permettant d’avoir des corrélation plus fortes entres les variables et les axes. On distingue plusieurs types de rotations :
- rotation orthogonale : quand on pense qu'il est possible de déterminer des facteurs indépendants les uns des autres. Il y a trois types de rotation orthogonale, la plus utilisée est VARIMAX ;
- rotation oblique : permet une corrélation entre les facteurs. Cette rotation est utilisée surtout avec l’AF et la méthode utilisée est OBLIMIN.
Sur le schéma de gauche, on a procédé à une rotation orthogonale et sur le schéma de droit, on a procédé à une rotation qui n’est pas orthogonale.
Les étapes de l’analyse factorielle de type exploratoire sont au nombre de sept :
- Déterminer les variables qui seront analysées ;
- Examiner cet ensemble de variables de manière conceptuelle et déterminer la solution qui apparaîtrait plausible quant au nombre de facteurs et au regroupement des variables ;
- Effectuer une analyse en composantes principales avec rotation orthogonale (varimax) en laissant la procédure définir le nombre de facteurs par défaut (le nombre de facteurs par défaut est déterminé par un critère, celui du eigenvalue plus grand que 1.0) ;
- Effectuer en même temps une analyse factorielle (lorsque c'est le but final de l’analyse) avec une rotation orthogonale et une rotation oblique (oblimin).
- Examiner les résultats pour déterminer les éléments suivants : comparer la solution proposée avec l'hypothèse de regroupement faite au départ. Pour chacune des variables, décider du maintien dans les analyses subséquentes à partir des deux critères suivants : [1] voir si la qualité de la représentation ("communality") est suffisamment importante (>0,20) pour le maintien dans l'analyse ; [2] voir si les variables appartiennent (saturation > 0,30) à un seul facteur ou à plusieurs. Une trop grande complexité d'une variable justifierait son retrait ;
- Examiner parallèlement la pertinence des regroupements et la pertinence théorique de maintenir ou de retirer une variable plutôt qu'une autre ;
- Examiner les divers indices de pertinence de la solution factorielle
- Refaire l’analyse pour arriver à une solution simple satisfaisante.
Concernant les outils de diagnostique de la solutions factorielles, il y a le déterminant de la matrice qui est un déterminant égal à zéro signifie qu’au moins une variable est une combinaison linéaire parfaite d’une ou de plusieurs autres variables . On cherche un déterminant très petit mais non égal à zéro Il y a aussi la mesure de Kaiser-Meyer-Olkin (KMO) qui est l’indice d'adéquation de la solution factorielle (l’ensemble des facteurs extraits). Un KMO élevé indique qu'il existe une solution factorielle statistiquement acceptable qui représente les relations entre les variables. Une valeur de KMO inférieure à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0.5} indique une mauvaise adéquation.
La question était quel type de voisin ne souhaitez-vous pas avoir. Les variables sont dichotomiques. Le déterminant de la matrice indique un déterminant de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0,195} . Il faut qu’il soit petit mais pas égale à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} .
Le seuil du KM0 est de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0,5} est ici on est à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0,803} .
On voit que toutes les variables ont un coefficient supérieur à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0,2} .
Ce tableau est le pourcentage de variance expliqué. Il y a dix variables. L’idée générale est que chaque variable a une valeur propre de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} . On cherche à retenir des dimensions qui on un poids supérieur à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} qui sont des dimensions susceptibles d’expliquer plusieurs dimensions. Si on additionne tous les chiffres, on obtient Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 10} . On va chercher des dimensions qui ont une valeur propre supérieure à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} . On calcule le pourcentage de variance expliqué par la dimension. C’est une analyse en composante principale qui s’intéresse à la variance commune et à la variance unique de chacune des dimensions. La deuxième dimension qui à une valeur de 13,7%.
Avec le test du coude (ou Scree test), on regarde le graphique des valeurs propres donne une représentation graphique des informations sur les valeurs propres de chaque facteur présentées dans le tableau des statistiques initiales. Ce test cherche le point (parfois les points) de cassure qui représente le nombre de facteurs au-delà duquel l'information ajoutée est insignifiante et peu pertinente. Les valeurs propres représentent la variance expliquée par chaque facteur.
Est représenté la valeur propre de chacune des dimensions. Avec le test du coude on regarde où il y a une cassure et à ce moment là, on ne retient plus la dimension. On retient uniquement les deux premières dimensions. Le critère absolu reste la capacité à interpréter les dimensions.
Si on demande une rotation, il y a un tableau qui correspond à la corrélation des variables avant la relations et un tableau qui correspond à aux variables après la rotation des variables. On a une variable corrélé avec plus ou moins deux dimensions. Si on regarde la corrélation des autres variables sur la deuxième dimension, elles sont beaucoup plus élevées. Il faut essayer d’interpréter chacune des dimensions.
C’est la transposition graphique du tableau précédent. Les dimensions sont centrées et réduites. Par exemple, « race » est à Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0,8} sur la première dimension, sur la seconde dimension. Chacune des dimensions doit s’interpréter de manière indépendante.
Un individu qui ne veut pas avoir un voisin qui est un travailleur émigré avait tendance à ne pas vouloir un voisin issu d’une autre race ou un voisin musulman ou qui a le sida.
Cela renvoie au concept de tolérance, on essaie de mesurer la tolérance des individus. Certaines se référent plus à des modes de vies alors que d’autres concernent des dimensions sur une forme de tolérance lié à ce que sont les gens et non pas à ce qu’ils sont. Plus on va vers des valeurs positives et plus ont est intolérant.
Le test d'une bonne analyse factorielle réside dans l’interprétation des résultats. C'est au chercheur de décoder la signification conceptuelle de chaque facteur. Un facteurs est une variable d’intervalle, c’est un facteur centré-réduit (moyenne = Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 0} , écart-type = Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} ) et il faut chercher à interpréter le pôle négatif et le pôle positif. Il faut également faire attention à la tendance à donner aux facteurs des noms qui font du sens mais qui ne reflètent pas ce qui a été mesuré.