Incertitude
De Baripedia
Sommaire
L’incertitude[modifier | modifier le wikicode]
Qu’est-ce qui est incertain en économie ?
- Futurs prix
- Future richesse
- Technologie future
- Actions des autres agents.
- ...
La plupart des individus n’aiment pas l’incertitude et se couvrent :
- Assurance.
- Portefeuilles financiers.
État de la nature[modifier | modifier le wikicode]
États de la nature possible:
- “accident de voiture” ()
- “pas d’accident de voiture” ().
L’accident arrive avec une proba. , rien ne se passe avec la probabilité complémentaire ;
Contingences[modifier | modifier le wikicode]
Un contrat qui implémente un paiement seulement en fonction de l’état du monde réalisé est contingent aux états du monde.
E.g. Un assureur ne paie que quand il y a un accident.
Préférences face à l’incertain[modifier | modifier le wikicode]
Ex.: Tire à pile ou face :
- Si Pile, gagne 100 CHF
- Si Face, perd 100 CHF
On appelle cela un pari juste car la Valeur Espérée (VE) =
Cependant, ce pari comporte un risque. Accepteriez-vous un tel pari ?
Trois attitudes face au risque[modifier | modifier le wikicode]
- Aversion au risque : refuse toujours un pari juste
- Goût pour le risque : accepte toujours un pari juste
- Neutralité face au risque : indifférent entre tous les paris justes (ne tient compte que de la VE)
Préférences face au risque[modifier | modifier le wikicode]
Pensez en terme de“Loterie”.
- Gain: avec probabilité 1/2 et gagne avec probabilité 1/2.
- , .
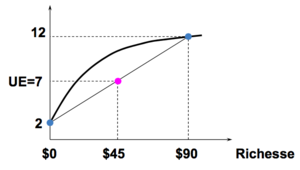
- Utilité espérée,
La valeur espérée de la loterie est,
- et .
- ⇒ avec certitude est préféré à la loterie ⇒ aversion au risque.
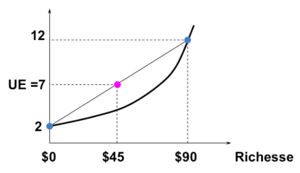
- ⇒ La loterie est préférée aux avec certitude⇒ goût pour le risque.
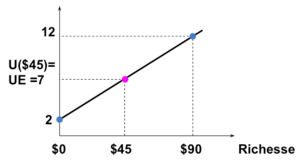
- ⇒ l’individu est indifférent ⇒ neutralité au risque.
L'utilité marginale est décroissante.
Assurance[modifier | modifier le wikicode]
Un agent averse au risque a un revenu et fait face à une probabilité de perdre un montant .
Il peut prendre une police d’assurance. Cette assurance lui rembourse un montant a en cas d’accident. Cette police lui coûte CHF.
Formellement, l’agent va chercher le montant d’assurance a qui maximise :
La condition de premier ordre donne : Échec d'analyse (erreur de syntaxe): {\displaystyle pu’(w - qa - L + a)(1 - q) - (1 - p)u’(w - qa)q = 0}
Soit, Échec d'analyse (erreur de syntaxe): {\displaystyle \frac {u'(w - qa - L + a)}{u' (w - qa)} = \frac {(1− p)q}{(1 − q) p}} .
Supposons un marché de l’assurance complètement concurrentiel.
Implique : Échec d'analyse (erreur de syntaxe): {\displaystyle profit\ espéré = 0} .
I.e. Échec d'analyse (erreur de syntaxe): {\displaystyle Profit\ espéré = qa – pa +(1 - p)0 = 0}
=>
Si le prix pour 1 CHF d’assurance = la probabilité d’accident, on dit que la police est juste.
Assurance “injuste”[modifier | modifier le wikicode]
Quand l’assurance est juste, le choix rationnel d’assurance : Échec d'analyse (erreur de syntaxe): {\displaystyle \frac {u’ (w - qa - L + a)}{u' (w - qa)} = 1} .
Donc l’agent s’assure complètement : .
Assurance “injuste”[modifier | modifier le wikicode]
Supposons que les assureurs font un profit économique positif.
I.e. Échec d'analyse (erreur de syntaxe): {\displaystyle qa – pa = (q - p)a > 0} .
Cela implique que .
Cela implique que .
i.e. les individus averses au risque ne prennent plus une assurance complète.
Les agents n’égalisent plus leur bien être entre les deux états du monde.
Diversification[modifier | modifier le wikicode]
Deux firmes, A et B. Une action coûte 10 $.
Avec une prob. 1⁄2, les profits de A sont de $100 et B $20.
Avec une prob. 1/2 les profits de A sont de $20 et B $100.
Vous avez 100 $ à investir. Stratégie ?
Si vous achetez seulement de A (ou seulement B).
$100/10 = 10 parts.
Vous gagnez $1000 avec prob. 1/2 et $200 avec prob. 1/2.
Gains espérés : .
En achetant 5 parts de chaque, vous gagnez $600 avec certitude !
La diversification a conservé la valeur espérée, en éliminant le risque.
Mutualisation[modifier | modifier le wikicode]
100 personnes neutres au risque font face à une perte potentielle de $10,000.
- Probabilité de perte = 0.01.
- Richesse initiale $40,000.
- Sans assurance, la valeur espérée est Échec d'analyse (erreur de syntaxe): {\displaystyle 0 ⋅ 99 \times $40,000 + 0 ⋅ 01($40,000 − $10,000) = $39,900} .
Assurance mutuelle, la perte espérée est Échec d'analyse (erreur de syntaxe): {\displaystyle 0⋅01 \times $10,000 = $100} .
Chacune des 100 personnes verse 1$ dans un fonds commun.
- Échec d'analyse (erreur de syntaxe): {\displaystyle $40,000 − $1 = $39,999 > $39,900} .
La mutualisation a bénéficié à tous !
Economie Comportementale[modifier | modifier le wikicode]
- Prospect Theory.
- Aversion aux pertes.
- Illusion du joueur.
- Effet de cadrage...
Prospect Theory[modifier | modifier le wikicode]
Les agents ont une perception biaisée des probabilités : la probabilité est transformée en une probabilité Échec d'analyse (erreur de syntaxe): {\displaystyle π(p)} .
Typiquement : Échec d'analyse (erreur de syntaxe): {\displaystyle π(p) > p} pour les faibles valeurs de (les agents mettent trop de poids sur les faibles probabilités).
Et Échec d'analyse (erreur de syntaxe): {\displaystyle π(p) < p} pour les hautes valeurs de (trop peu de poids sur les hautes probabilités).
Aversion aux pertes[modifier | modifier le wikicode]
Une personne possédant 1100 CHF et perdant 100 CHF se sent moins satisfait qu’une personne possédant 900CHF et trouvant 100 CHF.
Notion de « point de référence ».
Illusion du joueur (Gambler’s fallacy)[modifier | modifier le wikicode]
Idée que la probabilité d’un évènement issu d’un tirage aléatoire i.i.d (i.e. jeter une pièce) augmente (ou diminue) après une série d’évènements particulière.
i.e. après 10 «pile» on se dit « la prochaine est face avec 80% de chance » !
Effet de cadrage (Framing Effect)[modifier | modifier le wikicode]
Tirées de l’étude de Kahneman et Tversky (1981)
