Maximisation du Profit

En économie, le profit est les revenus moins les coûts.

• Profit = revenus – coûts.
• Revenus : Prix Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle x} Quantités vendues.
• Coûts : Coûts par unité produite Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle x} Quantités vendues.

NB : Coût par unité vendue dépend du prix des facteurs de production.

Une firme utilise des inputs Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle j = 1..., m} pour produire des biens Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle i = 1,... n} .

La quantité produite de chaque bien est Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle y_1,..., y_n} .

La quantité d’inputs est $x_{1},...,x_{m}$.

Le prix des biens est Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p_1, ... , p_n} .

Le prix des inputs est Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle w_1, ... , w_m} .

Cas simple

Nous considérons que la firme est dans un environnement compétitif: les prix Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p_1, ... , p_n} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle w_1, ... , w_m} sont donnés à la firme (elle ne peut pas les changer par elle même).

Nous allons étudier plus avant ce qu'est un environnement compétitif la séance prochaine.

Profit Economique

Le profit économique généré par le plan de production (Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle x_1, ..., x_m, y_1, ... , y_n} ) est : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \Pi = p_{1y_1} + \dots + p_{ny_n} - \dots w_m x_m} .

Une firme cherchera rationnellement à maximiser ses profits (son revenu sous contrainte de coût).

Courbe d’Iso Profit de Court Terme

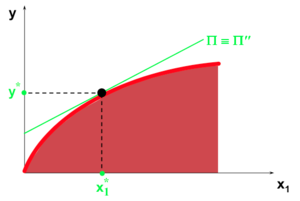
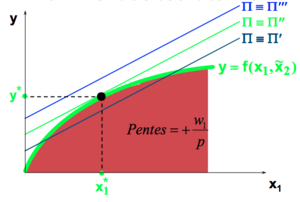
Une courbe d'Iso Profit contient tous les plans de production qui permettent d'atteindre un profit donné :

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \pi \equiv py - w_1x_1 - w_2 \widetilde{x}_2}

I.e.

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle y = \frac {w_1}{p}x_1 + \frac {\pi + w_2 \widetilde{x}_2}{p}}

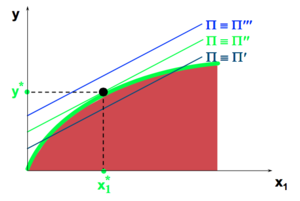
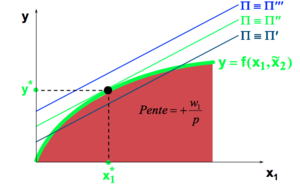
Le problème de la firme consiste à atteindre la courbe d'iso-profit la plus élevée possible sous contrainte de la fonction de production.

Optimum: pente iso profit et fonction de prod. De CT sont égales.

Maximisation du profit de court terme

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle Pm_1 = \frac {w_1}{p} \Leftrightarrow Pm_1 = w_1}

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p \times Pm_1} correspond à l'effet marginal de l'input Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 1} sur le revenu. À l'eq = à son prix.

Si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p \times Pm_1 > w_1} profit augmente avec Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle x_1} .

Si Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p \times Pm_1 < w_1} profit diminue avec Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle x_1} .

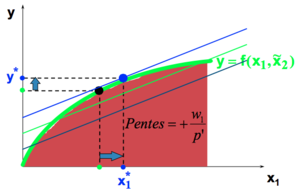
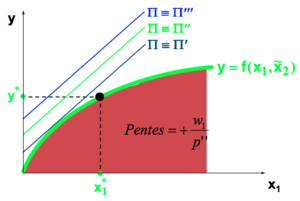
Changement de prix :

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle y = \frac {w_1}{p} \times x_1 + \frac {\pi + w_2 \widetilde{x}_2}{p}}

Une augmentation de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} cause :

• une diminution de la pente,
• une diminution de la constante.

Une augmentation de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p} cause donc,

• une augmentation de la quantité produite (l'offre de la firme est croissante dans les prix).
• une augmentation de la demande de la firme pour le facteur variable.

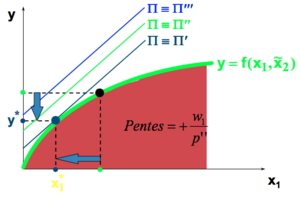
Changement du prix du facteur variable :

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle y = \frac {w_1}{p} \times x_1 + \frac {\pi + w_2 \widetilde{x}_2}{p}}

Une augmentation de Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle w_1} cause

• une augmentation de la pente
• aucun changement dans la constante.

Une augmentation du prix du facteur variable cause donc

• une diminution de la production,
• une diminution de l'utilisation du facteur variable.

Maximisation du profit de long terme

Désormais la firme peut choisir les niveaux de tous ses facteurs.

Il n'y a pas de coûts fixes quand on considère la décision de long terme.

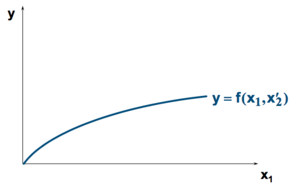
Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle y = \frac {w_1}{p} \times x_1 + \frac {\pi + w_2 \widetilde{x}_2}{p}}

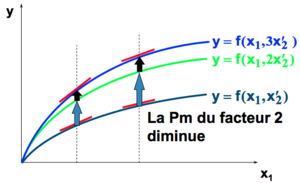
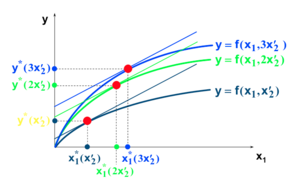
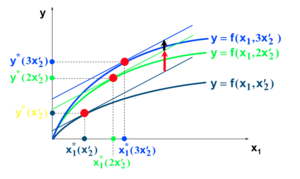
Une augmentation de l'input 2 cause :

• aucun changement dans la pente.
• une augmentation de la constante.

Et la productivité du facteur 1 augmente.

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p \times MP_1 - w_1 = 0} pour chaque plan de prod. de CT.

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p \times MP_1 - w_1 = 0}

Le profit va augmenter avec x2 tant que l'impact marginal de ce facteur respecte Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p \times Pm_2 - w_2 > 0}

La quantité du facteur 2 qui maximise le profit est donc Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p \times Pm_2 - w_2 = 0}

Et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p \times Pm_1 - w_1 = 0} est satisfait à l'éq. De court terme,

Les quantités d'inputs qui maximisent le profit de long terme sont donc celles qui amènent :

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p \times Pm_1 - w_1 = 0} et Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle p \times Pm_2 - w_2 = 0}

En mots, la contribution marginale d'un facteur au revenu est égale à son coût.

Maximisation du profit et rendements d'échelle

Si la technologie qu'utilise une firme (dans un environnement compétitif) a des rendements d'échelle décroissants, alors le plan de production qui maximise son profit est unique.

Rendements décroissants.

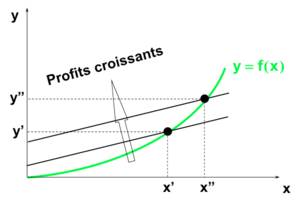
Si la technologie qu'utilise une firme (dans un environnement compétitif) a des rendements d'échelle croissants, alors le plan de production qui maximise son profit n'existe pas!

Une technologie avec des rendements croissants est incompatible avec un environnement compétitif.

En pratique ?

En partant d'un plan de production donné, qui apporte un profit positif, la firme peut doubler le nombre d'inputs, et ainsi doubler sa production et doubler son profit.

Donc des rendements constants demandent qu'une firme en compétition ne fasse aucun profit (mais aucune perte).