Incertitude

L’incertitude

Qu’est-ce qui est incertain en économie ?

• Futurs prix
• Future richesse
• Technologie future
• Actions des autres agents.
• ...

La plupart des individus n’aiment pas l’incertitude et se couvrent :

• Assurance.
• Portefeuilles financiers.

État de la nature

États de la nature possible:

• “accident de voiture” ($a$)
• “pas d’accident de voiture” ($na$).

L’accident arrive avec une proba. $p$, rien ne se passe avec la probabilité complémentaire $1-p$;

Contingences

Un contrat qui implémente un paiement seulement en fonction de l’état du monde réalisé est contingent aux états du monde.

E.g. Un assureur ne paie que quand il y a un accident.

Préférences face à l’incertain

Ex.: Tire à pile ou face :

• Si Pile, gagne 100 CHF
• Si Face, perd 100 CHF

On appelle cela un pari juste car la Valeur Espérée (VE) = ${\frac {1}{2}}\times 100+{\frac {1}{2}}\times -100=0$

Cependant, ce pari comporte un risque. Accepteriez-vous un tel pari ?

Trois attitudes face au risque

• Aversion au risque : refuse toujours un pari juste
• Goût pour le risque : accepte toujours un pari juste
• Neutralité face au risque : indifférent entre tous les paris justes (ne tient compte que de la VE)

Préférences face au risque

Pensez en terme de“Loterie”.

• Gain: $\$90$ avec probabilité 1/2 et gagne $\$0$ avec probabilité 1/2.
• $U(\$90)=12$, $U(\$0)=2$.
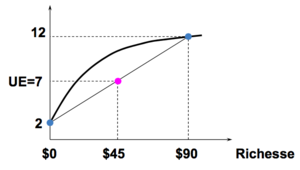
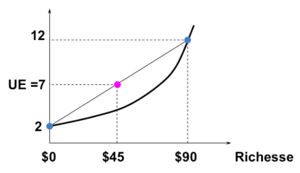
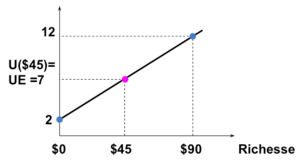
• Utilité espérée,

$UE={\frac {1}{2}}\times U(\$90)+{\frac {1}{2}}\times U(\$0)={\frac {1}{2}}\times 12+{\frac {1}{2}}\times 2=7$

La valeur espérée de la loterie est, $VE={\frac {1}{2}}\times \$90+{\frac {1}{2}}=\times \$0=\$45$

$UE=7$ et $VE=\$45$.

$U(\$45)>7$ ⇒ $\$45$ avec certitude est préféré à la loterie ⇒ aversion au risque.

$U(\$45)<7$ ⇒ La loterie est préférée aux $\$45$ avec certitude⇒ goût pour le risque.

$U(\$45)=7$ ⇒ l’individu est indifférent ⇒ neutralité au risque.

$U(\$45)>UE$ ⇒ aversion au risque.

L'utilité marginale est décroissante.

$U(\$45)<UE$ ⇒ Goût du risque.

$U(\$45)=UE$ ⇒ neutre au risque.

Assurance

Un agent averse au risque a un revenu $w$ et fait face à une probabilité $p$ de perdre un montant $L$.

Il peut prendre une police d’assurance. Cette assurance lui rembourse un montant a en cas d’accident. Cette police lui coûte $qa$ CHF.

Formellement, l’agent va chercher le montant d’assurance a qui maximise : $V=pu(w-qa-L+a)+(1-p)u(w-qa)$

La condition de premier ordre donne : Échec de l’analyse (erreur de syntaxe): {\displaystyle pu’(w - qa - L + a)(1 - q) - (1 - p)u’(w - qa)q = 0}

Soit, Échec de l’analyse (erreur de syntaxe): {\displaystyle \frac {u'(w - qa - L + a)}{u' (w - qa)} = \frac {(1− p)q}{(1 − q) p}} .

Supposons un marché de l’assurance complètement concurrentiel.

Implique : Échec de l’analyse (erreur de syntaxe): {\displaystyle profit\ espéré = 0} .

I.e. Échec de l’analyse (erreur de syntaxe): {\displaystyle Profit\ espéré = qa – pa +(1 - p)0 = 0}

=> $q=p$

Si le prix pour 1 CHF d’assurance = la probabilité d’accident, on dit que la police est juste.

Assurance “injuste”

Quand l’assurance est juste, le choix rationnel d’assurance : Échec de l’analyse (erreur de syntaxe): {\displaystyle \frac {u’ (w - qa - L + a)}{u' (w - qa)} = 1} .

Donc l’agent s’assure complètement : $a^{*}=L$.

Assurance “injuste”

Supposons que les assureurs font un profit économique positif.

I.e. Échec de l’analyse (erreur de syntaxe): {\displaystyle qa – pa = (q - p)a > 0} .

Cela implique que $q>p$.

Cela implique que $a^{*}<L$.

i.e. les individus averses au risque ne prennent plus une assurance complète.

Les agents n’égalisent plus leur bien être entre les deux états du monde.

Diversification

Deux firmes, A et B. Une action coûte 10 $.

Avec une prob. 1⁄2, les profits de A sont de $100 et B $20.

Avec une prob. 1/2 les profits de A sont de $20 et B $100.

Vous avez 100 $ à investir. Stratégie ?

Si vous achetez seulement de A (ou seulement B).

$100/10 = 10 parts.

Vous gagnez $1000 avec prob. 1/2 et $200 avec prob. 1/2.

Gains espérés : $\$500+\$100=\$600$.

En achetant 5 parts de chaque, vous gagnez $600 avec certitude !

La diversification a conservé la valeur espérée, en éliminant le risque.

Mutualisation

100 personnes neutres au risque font face à une perte potentielle de $10,000.

• Probabilité de perte = 0.01.
• Richesse initiale $40,000.
• Sans assurance, la valeur espérée est Échec de l’analyse (erreur de syntaxe): {\displaystyle 0 ⋅ 99 \times $40,000 + 0 ⋅ 01($40,000 − $10,000) = $39,900} .