Les entreprises en concurrence parfaite

En analysant le comportement des entreprises et les déterminants de l’offre de celles-ci sur le marché on distingue entre deux types de structure de marché :

1. Les marchés compétitifs où on trouve un grand nombre d’entreprises et chaque entreprise individuellement n’a pas d’impact sur le prix ;
2. Les marchés non compétitifs où les entreprises ont du pouvoir de marché et en changeant leur niveau de production (ventes) elles affectent les prix sur les marchés.

Dans ce chapitre nous nous concentrons sur les marchés compétitifs en examinant le rôle joué par les fonctions de coût de production des entreprises dans les décisions de produire ou ne pas produire et, si oui, quelles quantités. Dans les chapitres suivants nous allons analyser les principales formes de marché non-concurrentiel.

Un marché compétitif est un marché où il y a une infinité de vendeurs et acheteurs et où chacun d’entre eux a donc une part de marché infiniment petite (la taille de chacun est toute petite par rapport à la dimension du marché). Aucun agent économique n'est donc en mesure d’influencer le prix du marché en modifiant les quantités achetées ou vendues.

On peut également définir un marché compétitif comme étant un marché où :

1. le bien vendu est homogène (pas trop de différence entre les producteurs) ;
2. il y a un grand nombre d’acheteurs et des vendeurs ;
3. il y a libre entrée et sortie des acheteurs et vendeurs sur le marché.

Le résultant de ces trois conditions étant toujours qu'aucun acheteur ni vendeur pris individuellement ne peut influencer le prix sur le marché. Les actions d’un vendeur ou d’un acheteur isolé sur le marché ont un impact négligeable sur le prix et tous sont des ‘preneurs de prix’ (price takers).

Maximisation du profit

La recette

Le profit (Échec de l’analyse (erreur de syntaxe): {\displaystyle π} ) de l’entreprise est donné par la différence entre la recette totale ($RT$) et le coût total ($CT$).

Nous avons déjà analysé les fonctions de coût, mais pas encore les déterminants de la recette totale : Échec de l’analyse (erreur de syntaxe): {\displaystyle RT = Prix ∙ Quantité}

La RT est proportionnelle à la quantité vendue ($q$) car, dans un marché compétitif, le prix est donné.

La recette moyenne ($RM$) nous dit quel est le revenu que l’entreprise fait en moyenne par unité vendue : Échec de l’analyse (erreur de syntaxe): {\displaystyle RM = \frac {RT}{Quantité} = \frac{Prix \times Quantité}{Quantité} = Prix}

La recette marginale ($Rm$) nous dit quel est l’augmentation du revenu lorsque les quantités vendues ($q$) augmentent:

$Rm={\frac {\Delta RT}{\Delta q}}$ (= ${\frac {\partial RT}{\partial q}}$ pour des variations infinitésimales) Pour les firmes concurrentielles, la recette marginale est égale au prix du bien : $Rm={\frac {\Delta RT}{\Delta q}}=p$

Le profit

Les deux composantes du profit dépendent de la quantité produite :

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝜋(𝑞)=𝑅𝑇(𝑞) − 𝐶𝑇(𝑞)}

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝜋(𝑞)= 𝑝 \times 𝑞 − 𝐶𝐹 − 𝐶𝑉(𝑞)} (pour une entreprise concurrentielle)

Le profit moyen est :

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝜋_𝑀(𝑞) = 𝑅𝑀 − 𝐶𝑀(𝑞) = 𝑝 − 𝐶𝐹𝑀 − 𝐶𝑉𝑀(𝑞)}

Le profit marginal est :

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝜋_𝑚(𝑞) = 𝑅𝑚 − 𝐶𝑚(𝑞) = 𝑝 − 𝐶𝑚(𝑞)}

Le profit est maximisé quand le coût marginal est égal à la recette marginale : Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle max𝜋(𝑞) = 𝑅𝑇(𝑞) − 𝐶𝑇(𝑞)}

CPO (condition de premier ordre) :

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {\partial 𝜋}{\partial q} = \frac {\partial RT}{\partial q} - \frac {\partial CT}{\partial q} = Rm - Cm = p - Cm = 0}

À l’optimum $Rm=p=Cm$

Maximisation du π : un exemple numérique

NB: P = 6 € => RM = Rm = 6 €

Maximisation du π : analyse graphique

La firme décide de la quantité à produire de façon à maximiser ses profits et en raisonnant à la marge...

$q^{*}$ maximise la différence entre la recette totale et le coût total.

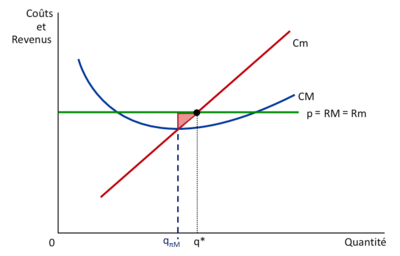
Cm versus CM

La firme décide de la quantité à produire de façon à maximiser

ses profits en raisonnant à la marge... et non pas en moyenne.

Si l'entreprise se limite à produire Échec de l’analyse (erreur de syntaxe): {\displaystyle q_πM} , c’est-à-dire la quantité qui maximise le profit moyen, elle renonce à réaliser des bénéfices nets.

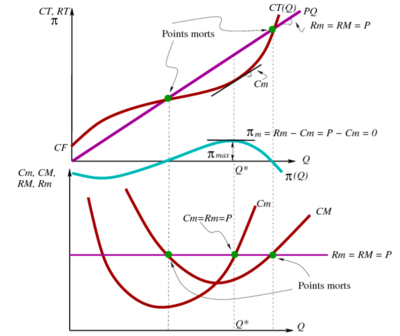
Maximisation du π : vue d'ensemble

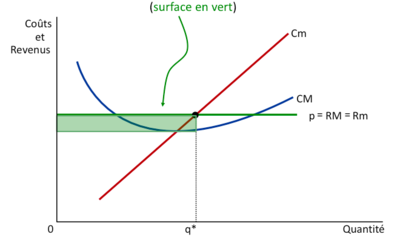
Profit

Le profit maximum est donné par la différence entre la RT et le CT au point $q^{*}$.

Échec de l’analyse (erreur de syntaxe): {\displaystyle π = RT - CT = RM ∙ q - CM ∙ q = (RM - CM) ∙ q = (p - CM ) ∙ q}

Maximisation du π : un exemple analytique

Fonction de coût : $CT=1+10q-q^{2}+{\frac {1}{3q^{3}}}$

Déterminez quelle est la quantité qui maximise le profit de l’entreprise en sachant que le prix de marché p est égal à 13.

CPO : $Cm=10-2q+q^{2}=13=p$

Échec de l’analyse (erreur de syntaxe): {\displaystyle q = \frac {2 ± \sqrt {4 - 4 \times 1 \times (-3)}}{2} = \frac {2 ± \sqrt {16}}{2} = \begin{vmatrix} frac\ {6}{2} > 0, ok\\ frac\ {-2}{2} = -1 < 0, exclus\end{vmatrix}}