Choix du consommateur

Maintenant que nous avons vu que ce que l’individu PEUT consommer, ce qu’il VEUT consommer, nous sommes armés pour analyser ce qu’il va consommer.

Rappelons que l’individu souhaite maximiser son bien-être, ou utilité, mais doit respecter la contrainte budgétaire. Le panier optimal obéira donc à cette double exigence.

Selon la réaction de la demande aux variations de revenu et de prix, nous pourrons distinguer différents types de biens.

De plus, la théorie du choix de consommation peut être utilisée pour analyser les décisions d'offre de travail et d'épargne (choix intertemporel).

Optimisation sous contrainte et courbe de demande

La choix optimal

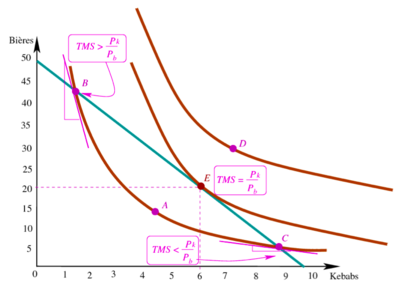
Une simple analyse graphique où l’on réunit la contrainte budgétaire et les courbes d’indifférence permet de montre de manière assez directe comment l'individu choisit le panier optimal.

Interprétation

Le panier $A$ est tel que la dépense est inférieure au revenu (il ne sera donc pas choisi par Amy).

Le panier $D$ n’est pas atteignable en l’état avec ce revenu.

Les paniers qui se trouvent le long de la contrainte budgétaire ne procurent

pas tous la même satisfaction à Amy.

Seul le panier $E$ maximise son bien-être, car le TmS (= taux d'échange "subjectif") en ce point est égal au prix relatif (= taux d’échange de marché) → la droite budgétaire est tangente à la courbe d’indifférence.

Le panier $B$

• respecte la contrainte,
• mais se trouve sur une courbe d’indifférence plus proche de l’origine = niveau de bien-être inférieur;
• le TmS y est plus grand que le taux d’échange: Amy peut accroître son bien-être en consommant davantage de kebabs.

Le panier $C$

• respecte aussi la contrainte,
• mais se trouve sur une courbe d’indifférence plus proche de l’origine;
• l’évaluation marginale subjective d’un kebab (le TmS) y est plus faible que le taux d’échange. Amy peut accroître sa satisfaction en réduisant sa consommation de kebabs.

Condition d'équilibre

L’équilibre se caractérise donc par l’égalité du TmS et du rapport des prix :

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑇𝑚𝑆 = \frac {𝑈𝑚𝐾}{UmB} = {𝑃_𝑘}{P_b}}

On peut également récrire cette équation d’équilibre comme suit :

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle \frac {𝑈𝑚𝐾}{P_k} = \frac {𝑈𝑚𝐵}{P_b}}

Um de la dépense sur les kebabs = Um de la dépense sur les bières

En effet, ${\frac {1}{p}}$ nous indique combien d’unités du bien l’individu peut acheter avec un franc et, multiplié par l’utilité marginale d’une unité du bien, ce rapport nous donne l’utilité marginale d’un franc dépensé sur le bien en question.

À l’équilibre, un franc dépensé en kebabs et un franc dépensé en bières doivent rapporter le même bien-être additionnel.

Démonstration formelle

Le problème du consommateur peut s’écrire :

Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle max𝑄_𝑏,𝑄_𝑘𝑈(𝑄_𝑏,𝑄_𝑘)} sous la contrainte: Échec de l’analyse (MathML avec SVG ou PNG en secours (recommandé pour les navigateurs modernes et les outils d’accessibilité) : réponse non valide(« Math extension cannot connect to Restbase. ») du serveur « https://en.wikipedia.org/api/rest_v1/ » :): {\displaystyle 𝑅 = 𝑃_𝑏 \times 𝑄_𝑏 + 𝑃_𝑘 \times 𝑄_𝑘}

Que l’on peut récrire en substituant 𝑄𝑘 par la contrainte dans 𝑈 𝑄𝑏 , 𝑄𝑘 : max𝑄𝑏𝑈 𝑄𝑏,(𝑅−𝑃𝑏 ∙𝑄𝑏)/𝑃𝑘

 Le maximum s’obtient par le respect de la condition de premier ordre (CPO): 𝜕𝑈(∙)=𝑈𝑚𝐵+𝑈𝑚𝐾∙ −𝑃𝑏 =0

 Autrement dit:

𝜕𝑄𝑏

𝑈𝑚𝐵=𝑈𝑚𝐾∙ 𝑃𝑏 𝑃𝑘

𝑃𝑘

𝑈𝑚𝐾=𝑃𝑘 𝑈𝑚𝐵 𝑃𝑏