Procesamiento de datos

Procesamiento de datos

Données clés

Faculté	Faculté des sciences de la société
Département	Département de science politique et relations internationales
Professeur(s)	Marco Giugni
Cours	Introduction aux méthodes de la science-politique

Lectures

• Cours introductif aux méthodes de la science-politique
• Le paradigme positiviste et le paradigme interprétatif
• Les méthodes scientifiques fondamentales
• De la théorie aux données
• Le recueil des données
• Le traitement des données

El análisis de los datos cuantitativos es muy diferente del análisis de los datos cualitativos; son dos prácticas de investigación muy diferentes, si no opuestas.

Nos centraremos en el análisis cuantitativo, que en realidad es más fácil que el análisis cualitativo de datos, aunque sólo sea porque hay rutinas institucionalizadas.

Languages

English

Français

Matriz de datos

Es una matriz que cruza los casos estudiados con una serie de variables, a saber, variables de columna y casos de fila.

Se debe asignar un código para excluir del análisis a los que no respondieron y para diferenciarlos de los que sí respondieron.

Hay tres análisis que corresponden a tres objetivos diferentes:

• análisis univariados: análisis que se realizan sobre una sola variable o característica.
• análisis bivariables: vinculando dos variables, queremos cruzar datos para analizar variaciones más sutiles como el interés de la política según la ciudad o la edad.
• análisis multivariados: pensamos que un fenómeno explicado nunca se explica por una sola variable independiente; por otro lado queremos introducir controles para controlar las relaciones a través de la técnica de purificación.

Hay que distinguir entre un análisis descriptivo que pretende describir una "situación de hecho" univariada o bivariada.

Tipos de análisis univariados

Tipos de variables y operaciones entre modalidades

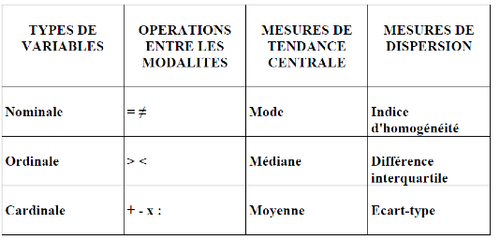
Existen diferentes tipos de análisis univariados, estas técnicas dependen del tipo de variable:

• variables nominales: sólo se pueden realizar operaciones de equivalencia o diferencia.
• variables ordinales: permite ordenar, es decir, categorizar según un orden desde el más pequeño hasta el más grande.

Nota: las variables ordinales y cardinales son categóricas, se basan en datos discretos, las distancias no se pueden ver.

• variables cardinales: además de las operaciones anteriores, permiten realizar las cuatro operaciones aritméticas básicas.

Medición central de tendencias

Al realizar un análisis cuantitativo, es necesario considerar el tipo de variables y luego elegir la herramienta a utilizar. Podemos distinguir entre dos tipos principales de medidas, es decir, entre dos tipos de información que queremos que tengan variables únicas:

• medidas de tendencia central
• medidas de dispersión.

Nota: dependiendo de la variable, las medidas son diferentes.

La media es una medida de valor de tendencia central que puede aplicarse a variables cardinales, pero no a variables categóricas. La mediana es la categoría que separa las series estadísticas en dos con el mismo número de casos por un lado y por el otro.

Esta es una información importante que constituye el punto de partida para este tipo de descripción de datos para determinar qué hacer a continuación en el caso de análisis más sofisticados.

Medición de dispersión

También se distinguen las medidas de dispersión: la medida básica es la desviación estándar, que es una medida estandarizada que varía de -1 a +1 de la varianza, que es la medida que indica cómo se distribuyen los individuos.

La varianza es muy importante para calcular la probabilidad de error. Se requieren diferentes medidas dependiendo de la unidad de medida de la variable y la medida de la tendencia central y la dispersión, como la desviación estándar, que es el coeficiente clave, debe tenerse en cuenta a lo largo del análisis cuantitativo.

Tipos de análisis bivariados

En este contexto, deseamos cruzar características en una perspectiva descriptiva o explicativa. Dependiendo del tipo de variable, existen diferentes técnicas para analizar y procesar los datos.

Se deben considerar tanto las variables dependientes como las independientes. Al cruzar, debemos mirar la variable dependiente e independiente para ver si se trata de variables categóricas u ordinales que permiten distinguir tres familias principales de tipos de análisis:

• variables categóricas / nominales - nominales: se realizan tablas de contingencia, no se pueden utilizar otras técnicas. La mayor parte del tiempo en la ciencia política se trata de este tipo de variables, porque las respuestas dan lugar a variables ordinales. Existen coeficientes que nos permiten dar una medida única de la relación entre estas dos variables, como la V de Cramer, que nos permite ver la asociación entre variables categóricas. Para interpretar, es importante que el porcentaje total se refiera siempre a las categorías de la variable independiente; queremos ver cómo la distribución de la variable dependiente depende de las funciones de la variable independiente. La indicación del número de casos muestra si el proceso es estadísticamente representativo, ya que el tamaño de la muestra afecta a la medición.
• variables cardinales - cardinales: ya no hacemos una tabulación cruzada, utilizamos otras herramientas y en particular la herramienta de regresión y correlación:
  • covariable: cuando hay dos variables continuas, cuando una aumenta la otra aumenta proporcional o inversamente proporcional, las dos variables están vinculadas en esta dirección.
  • correlación: es simplemente un covariable estandarizado, es decir, está entre -1 y +1. Estandarizamos para asegurar que se comparen las variables que se miden de manera diferente en la base; si, por ejemplo, tenemos escalas de 0 a 10 y escalas de 0 a 5, no podemos comparar estas variables, entonces debemos asegurarnos de que esta información esté estandarizada. Las variables pueden repetirse en la misma escala o software que calcula una correlación estandarizada.
  • regresión: en una correlación estamos en una perspectiva descriptiva, no intentamos ver una dirección de causalidad en una regresión queremos ver si dos variables están asociadas, vinculadas, correlacionadas.

• variables independientes nominales - variables dependientes cardinales: no se pueden aplicar tabulaciones cruzadas, correlaciones y regresiones; se realiza un análisis de varianza o covarianza, cuyo caso más simple es una comparación de promedios, que podría ser, por ejemplo, el número de veces que los individuos participan en una elección según el cantón.

Regresión lineal

C’est un ensemble très varié et parfois complexe d’outils, mais c’est l’outil principal. La régression linéaire est l’élément principal ; une bonne partie des analyses quantitatives faites en science sociale s’appuient sur la régression linéaire.

On parle de linéarité, car on postule qu’il y a une relation linéaire entre les variables qu’on étudie, en d’autres termes il y a une fonction linéaire derrière cette relation ; cependant, on peut aussi envisager des régressions qui ne sont pas que linéaires.

On présuppose que ce qu’on veut expliquer est une fonction linéaire d’une ou plusieurs variables indépendantes. Cela est crucial, car la régression linéaire n’est qu’un sous-ensemble d’une famille plus large d’analyses de régressions qui ne se base pas sur une idée de linéarité entre les deux variables.

Le modèle le plus simple est avec une variable explicative comme, par exemple, la participation politique en fonction de l’intérêt pour la politique.

En terme descriptif il y a une forte corrélation entre ces deux variables ; si une hypothèse dit que c’est l’intérêt pour la politique qui influence la participation alors on fait une analyse de régression.

On a toujours le problème de l’endogénéité dans ce type d’analyse, on postule que l’intérêt pour la politique détermine une participation ; on pourrait aussi postuler que plus on participe plus on développe un intérêt pour la politique.

La participation politique est une fonction linéaire de l’intérêt pour la politique « plus » un facteur constant à savoir la valeur de Y lorsque X est égal à 0 c’est-à-dire quel est mon niveau de participation lorsque l’intérêt pour la politique est nul. Au fond c’est où la droite de régression croise l’axe des ordonnées.

Dans l’analyse multivariée, il y a toujours une marge d’erreur ; une chose est liée si on des données du sondage liées à la marge d’erreur entre population et échantillon, mais indépendamment qu’on soit en train de travailler sur des échantillons ou une population globale ; il y a un terme d’erreur qui intervient, car il y a toujours quelque chose qui influence ce qu’on veut expliquer et qui n’est pas inclus dans le modèle de régression comme, par exemple, l’éducation, l’âge, le contexte social, institutionnel, etc.

En fait, le E regroupe la variance non expliquée à savoir tout ce qui pourrait expliquer Y, mais n’est pas introduit dans le modèle, c’est le problème de la sous-spécification du modèle à savoir l’enjeu concernant la spécification du modèle ; plus un modèle a plus de variables plus il risque d’être sous-spécifié et moins on explique de variations dans le Y et plus le E en termes d’erreur est élevé, on veut réduire au maximum le E.

Ceci permet de dire que le fait de ne pas inclure certaines variables dans un modèle explicatif à deux conséquences majeures :

• le modèle est sous-spécifié, on explique peu la variabilité de Y avec ce modèle c’est-à-dire les facteurs fortement corrélés avec ce que l’on souhaite étudier.
• la deuxième raison est liée au contrôle des variables, car si on introduit l’intérêt pour la politique, une troisième variable peut influencer l’intérêt pour la politique et la participation pour la politique ; l’association est fallacieuse.

On veut inclure le maximum de variables dont on pense qu’elle peut influencer directement Y ou indirectement faisant que la relation entre X et Y soit fausse ou seulement apparente.

Le B est le coefficient de régression à savoir la pente de la droite de régression donnant la force de l’effet du X car il est multiplicatif par X c’est-à-dire que plus l’effet de X est fort plus B est élevé.

Le B peut être non standardisé ou standardisé. « Standardisation » signifie normaliser et le but est de pouvoir comparer des coefficients différents.

On est dans une logique additive, il y a des « + » ; on suppose que la variation de Y est une fonction linéaire est additive ou cumulée de l’effet de toutes les autres variables introduites dans le modèle.

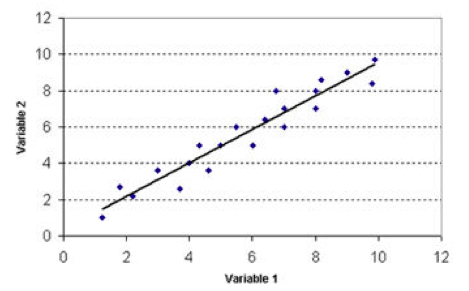
Droite de régression

La droite de régression représente la fonction de régression linéaire. On veut regarder de combien augmente Y lorsqu’on augmente X. admettons que les (0 ; 12) sont l’intérêt pour la politique et l’autre la participation politique; on peut voir qu’il y a une corrélation assez forte entre les deux, lorsqu’on a une augmentation de l’intérêt pour la politique on augmente la participation politique.

Les points bleus représentent les cas, la droite de régression est l’estimation des valeurs et donc on va regarder dans quelle mesure et comment cette droite rencontre un nuage de points.

La qualité du modèle a à voir à la qualité de l’estimation qui dépend beaucoup de la manière dont sont distribués les points. Il est possible que le nuage de point soit estimé pour une droite qui a la même pente, toutefois la qualité de cet effet est le même alors qu’il est diffèrent parce que la droite ne fait qu’une approximation beaucoup plus précise du nuage de points ou les points sont proches de la droite.

Il faut retenir que l’un des principaux instruments privilégiés pour l’analyse quantitative lorsqu’on a à faire à des variables intervalles ou cardinal et l’analyse de la corrélation ou de la régression.

L’idée de la régression linéaire qui est un sous-ensemble d’un ensemble plus vaste se base sur l’idée d’une fonction linéaire entre X et Y ; on essaie d’estimer un nuage de points qui représente le croisement entre les deux variables dans l’échantillon donc on va analyser la droite de régression et sa pente. Si la pente est de 0 alors Y ne change pas quand on change X, on peut être très intéressé à la politique, mais on y participe toujours au même niveau.

Analyses multivariées

Analyse de régression

Selon le type de variables que l’on souhaite expliquer, on peut ou on ne peut pas appliquer l’outil de régression linéaire, il y a par exemple la régression logistique dans le cas de variables dummies soit absence ou présence, on ne peut appliquer la régression linéaire, car les présupposés de base ne sont pas garantis.

Analyse des chemins causaux (path analysis)

Un des problèmes de l’analyse de la régression est qu’on suppose que Y est une fonction linéaire de la somme de toutes les variables indépendantes or se faisant on regarde que les effets directs des variables d’un modèle ; toutefois que se passe-t-il lorsqu’on veut regarder des effets indirects ?

On fait une analyse des « chemins causaux » ; il y a des coefficients de régression qui peuvent être significatif ou pas, mais on peut voir des chemins causaux c’est-à-dire qu’on peut voir de quelle manière les valeurs de gauche influence la participation non pas directement, mais indirectement à savoir que le fait d’être de gauche fait qu’on a plus de probabilités d’être intégré dans certains types de réseau développent un internet pour un certain enjeu qui permet de développer un sentiment d’efficacité individuel faisant qu’on a une intensité plus forte de participation. On introduit des variables intermédiaires.

Au lieu d’avoir une indication, on en a plusieurs parce que chaque variable peut ou est une variable dépendante, on fait une somme d’équations.

Analyse factorielle

C’est une analyse qui a pour objectif de réduire la complexité qu’on peut avoir lorsqu’on a une matrice de données avec beaucoup de variables et de cas et que l’on veut avoir un index plus succinct.

Lorsqu’on a parlé d’opérationnalisation des concepts complexes, on est arrivé à une dernière étape de construction ; l’analyse factorielle permet de construire des index par l’analyse des liens sous-jacents qui expliquent la variation sur un ensemble multiple d’indicateurs.

C’est un outil fréquemment utilisé en science politique et notamment lorsqu’on étudie les changements de valeurs.

Analyse multiniveaux

Auparavant toutes les mesures concernaient les variables individuelles, maintenant il y a des propriétés du contexte qui ne sont pas de l’individu qui peuvent influencer la participation politique comme le système électoral ou le type de système politique.

Dans une optique de régression normale il y a des manières de court-circuiter le problème, on ne peut intégrer les facteurs contextuels dans l’analyse on peut simplement comparer.

L’analyse multiniveau permet de faire une analyse de régression multiniveau, on ajoute des propriétés du contexte et pas seulement des propriétés individuelles ; on intègre des propriétés individuelles et contextuelles. Il y a ce développement important en sciences politiques.

Type de méthodes qualitatives

On peut faire une distinction entre l’analyse de contenu et l’analyse de discours. Ces termes ne font pas le consensus dans la littérature, certains estiment que l’analyse de discours est un type d’analyse de contenu et pour d’autres ce n’est pas le cas.

Analyse de contenu

L’analyse de contenu s’intéresse au poids, elle est plus descriptive, elle s’intéresse aux différents enjeux soulevés par des personnes. On peut faire une distinction ultérieure :

• thématique : on compte le nombre de fois qu’un tel thème apparaît dans un discours.
• lexicale : analyse basée sur l’analyse des occurrences ou cooccurrences à savoir une analyse qualitative qui a des éléments d’analyse quantitative.

Analyse de discours

C’est une analyse interprétative, on parle d’une famille de techniques, on peut dire qu’on s’intéresse à comment et aux effets d’un discours donné.

Pour simplifier, l‘analyse de contenu est plutôt descriptive et l’analyse de discours explicatif.

Étapes de l’analyse thématique

Il y a cinq grandes étapes :

1. familiarisation (préanalyse) : il faut d’abord se familiariser avec le matériel à disposition.
2. identification d’un cadre thématique (schéma de codage, index) : manière de coder l’information soit d’identifier le cadre thématique.
3. indexation (codage) : réduire l’information.
4. cartographie (catégorisation et réduction des données) : création de typologies, de classifications, réduction des données afin de pouvoir les interpréter.
5. mapping et interprétation (analyse et interprétation)

Étapes de l’analyse de discours

• Préanalyse
• Identification d'éléments pertinents
• Analyse systématique à partir des éléments identifiés